Experimental Study of the Space–Time Effect of a Double-Pipe Frozen Curtain Formation with Different Groundwater Velocities
Abstract
:1. Introduction
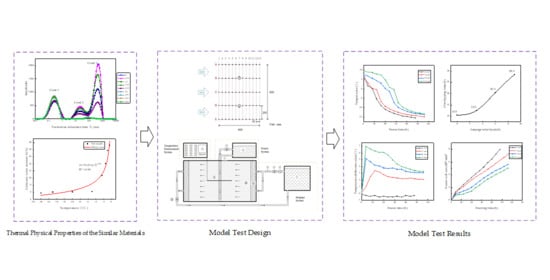
2. Experimental Study on Thermal Physical Properties of the Similar Materials
2.1. Selection of the Similar Materials
2.2. Test Method and Test Equipment
2.3. Test Results
3. Double-Pipe Freezing Model Test with Flowing Groundwater
3.1. Model Test Design
3.2. Test System and Measuring Point Layout
3.3. Test Scheme and Test Process
4. Temporal and Spatial Evolution of Temperature Field in Double-Pipe Freezing
4.1. Change of Temperature with Freezing Time
4.2. Spatial Distribution of Temperature Field
5. Analysis of the Formation Process of Frozen Curtain
5.1. Influence of the Flow on Overlapping Time of Frozen Curtain
5.2. Influence of the Flow on the Development of Frozen Curtain Area
5.3. Influence of the Flow on Shape Characteristics of the Frozen Curtain
6. Conclusions
- Based on NMR method, the saturated sand layer was studied, and it was found that the content of unfrozen water decreased rapidly between −0.5 °C and −2.5 °C, and the freezing temperature of the saturated sand was −0.5 °C. The relationship between the unfrozen water content and the temperature in the sand layer was further fitted, and it was found that the relationship between the unfrozen water content and the temperature satisfied the power function. For the saturated sand layer, the two parameters were α = 15.67 and β = −0.38.
- The flow led to the difference of the temperature evolution between upstream and downstream. During the process of freezing, in the positive temperature zone, the upstream temperature reducing rates at B3 were 0.53 °C/h, 0.39 °C/h, 0.26 °C/h, and 0.27 °C/h for the four velocities. In the negative temperature zone, the rates of the temperature reduction were stable near 0.20 °C/h. The rate of the temperature reduction in the upstream was larger than that in the downstream, and the flow had little effect on the reducing rate in the negative temperature zone. C7 was located between the two freezing pipes. Because of the superposition effect of the two freezing pipes, the reduction rate of the whole process was larger than that of B3 and B11. In the positive temperature zone, the rates of the temperature reduction at C7 were 0.8 °C/h, 0.7 °C/h, 0.38 °C/h, and 0.34 °C/h. In the negative temperature zone, the temperature reducing rates for different velocities were about 0.35 °C/h.
- In the space, because of the flow, the downstream temperature was lower than the upstream temperature. Additionally, the larger the velocity, the larger the temperature difference. The temperature difference at the symmetrical points first increased, then decreased, and finally tended to be stable. When u = 3 m/d, 6 m/d, and 9 m/d, the maximum differences between B1 and B13 were 3.4 °C, 5.2 °C, and 7 °C, respectively. At the end of the test, the differences were stable at 2.1 °C, 3.1 °C, and 3.3 °C, respectively.
- The flow prolonged the overlapping time of the frozen curtains. Compared with u = 0 m/d, the overlapping times at u = 3 m/d, 6 m/d, and 9 m/d were increased by 20%, 95%, and 180%, respectively. The development of the frozen curtain was inhibited by the flow. The larger the velocity, the slower the development of the frozen curtain. There was a linear positive correlation between the area of the frozen curtain and the freezing time. With the four velocities, the average development rates of the frozen curtain area in the whole freezing process were 16,662 mm2/h, 12,936 mm2/h, 10,072 mm2/h, and 8986 mm2/h. The statistical analysis of the frozen curtain thicknesses Rs, Ru, and Rd at the three locations showed that the developments of Rs, Ru, and Rd were all inhibited by the flow. The larger the velocity, the more obvious the inhibition. Compared with the development rates when u = 0 m/d, the development rates of Rs, Ru, and Rd at u = 9 m/d decreased by 42%, 32%, and 14%, respectively. The flow had the greatest inhibitory effect on the side thickness of the frozen curtain Rs, and it had the smallest inhibitory effect on the downstream thickness of the frozen curtain Rd.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Russo, G.; Corbo, A.; Cavuoto, F.; Autuori, S. Artificial ground freezing to excavate a tunnel in sandy soil. measurements and back analysis. Tunn. Undergr. Space Technol. 2015, 50, 226–238. [Google Scholar] [CrossRef]
- Wang, B.; Rong, C.X.; Cheng, H.; Yao, Z.S.; Cai, H.B. Research and application of the local differential freezing technology in deep alluvium. Adv. Civil. Eng. 2020, 2020, 9381468. [Google Scholar] [CrossRef]
- Gallardo, A.H.; Marui, A. The aftermath of the fukushima nuclear accident: Measures to contain groundwater contamination. Sci. Total Environ. 2016, 547, 261–268. [Google Scholar] [CrossRef]
- Huang, X.W.; Yao, Z.S.; Cai, H.B. An analytical heat-transfer model for coaxial borehole heat exchanger with segmented method. Energy Source Part A 2020, 10, 1851821. [Google Scholar] [CrossRef]
- Lin, J.; Cheng, H.; Cai, H.B.; Tang, B.; Cao, G.Y. Effect of seepage velocity on formation of shaft frozen curtain in loose aquifer. Adv. Mater Sci Eng. 2018, 2018, 2307157. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.M.; Chen, J.; Sugimoto, M.; Ge, H.Y. Numerical simulation model of artificial ground freezing for tunneling under seepage flow conditions. Tunn. Undergr. Space Technol. 2019, 92, 103035. [Google Scholar] [CrossRef]
- Lao, L.Y.; Ji, Z.Q.; Huang, L.L.; Li, S.J. Research on the temperature field of a partially freezing sand barrier with groun-water seepage. Sci. Cold Arid Reg. 2017, 9, 280–288. [Google Scholar]
- Pimentel, E.; Sres, A.; Anagnostou, G. Large-scale laboratory tests on artificial ground freezing under seepage-flow conditions. Geotechnique 2012, 62, 227–241. [Google Scholar] [CrossRef]
- Wang, B.; Rong, C.X.; Lin, J.; Cheng, H.; Cai, H.B. Study on the formation law of the freezing temperature field of freezing shaft sinking under the action of large-flow-rate groundwater. Adv. Mater. Sci. Eng. 2019, 2019, 1670820. [Google Scholar] [CrossRef] [Green Version]
- Alzoubi, M.A.; Xu, M.H.; Hassani, F.P.; Poncet, S.; Sasmito, A.P. Artificial ground freezing: A Review of thermal and hydraulic aspects. Tunn. Under. Space Techno. 2020, 104, 1–18. [Google Scholar] [CrossRef]
- Alzoubi, M.A.; Nie-Rouquette, A.; Sasmito, A.P. Conjugate heat transfer in artificial ground freezing using enthalpy-porosity method: Experiments and model validation. Int. J. Heat Mass Trans. 2018, 126, 740–752. [Google Scholar] [CrossRef]
- Alzoubi, M.A.; Madiseh, A.; Hassani, F.P.; Sasmito, A.P. Heat transfer analysis in artificial ground freezing under high seepage: Validation and heatlines visualization. Int. J. Therm. Sci. 2019, 139, 232–245. [Google Scholar] [CrossRef]
- Alzoubi, M.A.; Sasmito, A.P.; Madiseh, A.; Hassani, F.P. Intermittent freezing concept for energy saving in artificial ground freezing systems. Energy Procedia. 2017, 142, 3920–3925. [Google Scholar] [CrossRef]
- Vitel, M.; Rouabhi, A.; Tijani, M.; Guérin, F. Thermo-hydraulic modeling of artificial ground freezing: Application to an underground mine in fractured sandstone. Comput. Geotech. 2016, 75, 80–92. [Google Scholar] [CrossRef]
- Vitel, M.; Rouabhi, A.; Tijani, M.; Guérin, F. Modeling heat and mass transfer during ground freezing subjected to high seepage velocities. Comput. Geotech. 2016, 73, 1–15. [Google Scholar] [CrossRef]
- Huang, S.B.; Liu, Q.S.; Cheng, A.P.; Liu, Y.Z.; Liu, G.F. A fully coupled thermo-hydro-mechanical model including the determination of coupling parameters for freezing rock. Int. J. Rock Mech. Min. 2018, 103, 205–214. [Google Scholar] [CrossRef]
- Hu, J.; Liu, Y.; Li, Y.P.; Yao, K. Artificial ground freezing in tunnelling through aquifer soil layers: A case study in Nanjing Metro Line 2. KSCE J. Civ. Eng. 2018, 22, 4136–4142. [Google Scholar] [CrossRef]
- Zhou, X.M.; Wang, M.S.; Zhang, X.Z. Model test research on the formation of freezing wall in seepage ground. J. China Coal Soc. 2005, 30, 196–201. (In Chinese) [Google Scholar]
- Wang, Z.H.; Zhu, X.R.; Zhu, G.X. The experimental researches on the ground freezing with liquid nitrogen under water flowing. J. Zhejiang Univ. 1998, 32, 534–540. (In Chinese) [Google Scholar]
- Sudisman, R.A.; Osada, M.; Yamabe, T. Experimental investigation on effects of water flow to freezing sand around vertically buried freezing pipe. J. Cold Reg. Eng. 2019, 33, 04019004. [Google Scholar] [CrossRef] [Green Version]
- Shan, R.L.; Liu, W.J.; Chai, G.J.; Xiao, S.C. Experimental study on influencing factors of characteristic index of local horizontal frozen body of double-row pipe under seepage. Adv. Mater. Sci. Eng. 2020, 2020, 8267692. [Google Scholar] [CrossRef] [Green Version]
- Yang, X.; Ji, Z.Q.; Zhang, P.; Qi, J.L. Model test and numerical simulation on the development of artificially freezing curtain in sandy layers. Transp. Geotech. 2019, 21, 100293–100376. [Google Scholar] [CrossRef]
- Wang, B.; Rong, C.X.; Cheng, H.; Cai, H.B.; Zhang, S.Q. Analytical solution of steady-state temperature field of single freezing pipe under action of seepage field. Adv. Civ. Eng. 2020, 2020, 5902184. [Google Scholar] [CrossRef]
- Wang, B.; Rong, C.X.; Cheng, H.; Cai, H.B.; Dong, Y.B.; Yang, F. Temporal and spatial evolution of temperature field of single freezing pipe in large velocity infiltration configuration. Cold Reg. Sci. Technol. 2020, 175, 5902184. [Google Scholar] [CrossRef]
- Marwan, A.; Zhou, M.M.; Abdelrehim, M.Z.; Meschke, G. Optimization of artificial ground freezing in tunneling in the presence of seepage flow. Comput. Geo. Tech. 2016, 75, 115–125. [Google Scholar] [CrossRef]
- Huang, S.B.; Guo, Y.L.; Liu, Y.Z.; Ke, L.H.; Liu, G.F.; Chen, C. Study on the influence of water flow on temperature around freeze pipes and its distribution optimization during artificial ground freezing. Appl. Therm. Eng. 2018, 135, 435–445. [Google Scholar] [CrossRef]
- Liu, H.W.; Zhang, X.F.; Leng, Y.F. Testing analysis on influencing factors of unfrozen water of frozen earth. North Commun. 2010, 9, 22–24. (In Chinese) [Google Scholar]
- Tan, L.; Wei, C.F.; Tian, H.H.; Zho, J.Z.; Wei, H.Z. Experimental study of unfrozen water content of frozen soils by low-field nuclear magnetic resonance. Rock Soil Mech. 2015, 36, 1566–1572. (In Chinese) [Google Scholar]
- Anderson, D.M.; Tice, A.R. Predicting unfrozen water contents in frozen soils from surface area measurements. Highw. Res. Rec. 1972, 393, 12–18. [Google Scholar]
- Lu, J.G.; Pei, W.S.; Zhang, X.Y.; Bi, J.; Zhao, T. Evaluation of calculation models for the unfrozen water content of freezing soils. J. Hydol. 2019, 575, 976–985. [Google Scholar] [CrossRef]



















| Dry Density (kg/m3) | Saturated Density (kg/m3) | Porosity | Saturated Moisture Content | Permeability Coefficient (m/s) | Thermal Conductivity (W/mK) |
|---|---|---|---|---|---|
| 1612 | 1942 | 0.32 | 19.9% | 2.28 × 10−4 | 2.25 |
| Geometric Similarity Ratio Cl | Temperature Similarity Ratio CT | Time Similarity Ratio Ct | Velocity Similarity Ratio Cu |
|---|---|---|---|
| 1/3 | 1 | 1/9 | 3 |
| Flowing Velocity (m/d) | 0 | 3 | 6 | 9 |
|---|---|---|---|---|
| Development rate of Rs (mm/h) | 5.6 | 4.4 | 3.3 | 3.2 |
| Development rate of Ru (mm/h) | 9.2 | 8 | 6.9 | 6.2 |
| Development rate of Rd (mm/h) | 9.1 | 8.2 | 7.9 | 7.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, S.; Rong, C.; Cheng, H.; Wang, B.; Jiang, X.; Zhang, W.; Halliru, Y. Experimental Study of the Space–Time Effect of a Double-Pipe Frozen Curtain Formation with Different Groundwater Velocities. Energies 2021, 14, 3830. https://doi.org/10.3390/en14133830
Sun S, Rong C, Cheng H, Wang B, Jiang X, Zhang W, Halliru Y. Experimental Study of the Space–Time Effect of a Double-Pipe Frozen Curtain Formation with Different Groundwater Velocities. Energies. 2021; 14(13):3830. https://doi.org/10.3390/en14133830
Chicago/Turabian StyleSun, Shicheng, Chuanxin Rong, Hua Cheng, Bin Wang, Xiaogang Jiang, Wei Zhang, and Yunusa Halliru. 2021. "Experimental Study of the Space–Time Effect of a Double-Pipe Frozen Curtain Formation with Different Groundwater Velocities" Energies 14, no. 13: 3830. https://doi.org/10.3390/en14133830
APA StyleSun, S., Rong, C., Cheng, H., Wang, B., Jiang, X., Zhang, W., & Halliru, Y. (2021). Experimental Study of the Space–Time Effect of a Double-Pipe Frozen Curtain Formation with Different Groundwater Velocities. Energies, 14(13), 3830. https://doi.org/10.3390/en14133830