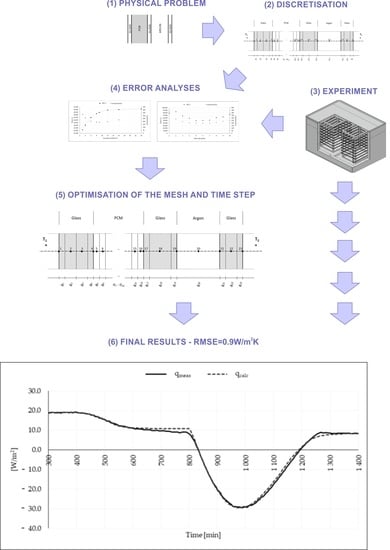
Heat Transfer with Phase Change in a Multilayer Construction: Simulation versus Experiment

Abstract

The latent heat storage in the layer of phase change material (PCM) exposed to dynamic changes in boundary temperature was investigated numerically and experimentally. The original numerical model of heat transfer with phase change using a mushy volume approach was proposed and validated. The main improvement in the proposed model in comparison to others is that the compaction of the mesh and longitude of the time step were chosen after analysis of its impact in the field of error. The model was tested in the case of thin layer structure of the triple glazing window with one cavity filled with phase change material paraffin RT18HC. The experimental validation was carried out in the climatic chamber under dynamic changes in external temperature (from 10 to 50 °C) in a daily cycle. The highest accuracy was obtained for space discretization of the control volume 1 mm thick (12 CV for 12 mm of PCM layer) and 5 min time step. The obtained RMSE values, although they cannot be directly compared because of the very different approaches to the simulations, show that the proposed algorithm is sufficiently accurate for the assessment of energy storage in the PCM window. Both the simulation and experiment proved that, under specific conditions, implementation of the PCM into the structure resulted in delaying the peak for around 4 h.

1. Introduction

Effective storage of heat gains [1] has become an increasingly important issue in any case of highly dynamic, complex energy systems [2], e.g., ultra-low or plus energy buildings [3]. Moreover, the buildings of the future will need to be fully automated and smart controlled [4] to provide a very high indoor quality and to be resilient to possible climate change [5]. Possible future climate scenarios [6] show that the weather will become more extreme with a short-term variation in climate variables [7]. Moazami et al. revealed that, depending on the type of building, the relative change in peak load for cooling demand under near future extreme conditions could be up to 28.5% higher compared with typical conditions. It has been found that there is an increased probability of heat waves occurring with high temperature increases in the future climate, i.e., future heat waves could be more severe [8]. Diurnal variation in warming under climate scenarios is perhaps more important than annual or even daily averages; although, this is far less studied [9]. According to such scenarios, an effective heat storage system design for a daily or weekly cycle should be considered for future buildings [10]. The significant benefits of using PCM are that it can obtain peak load reduction (from 10 to 57%), the overall cost savings (from 11 to 96.6%) and improved thermal comfort. In the case of new construction technologies, it should be noted that most the new buildings are designed in lightweight construction [11] with a high level of window to external wall ratio. Only the application of walls with a density of 1000 kg/m³ resulted in a reduction in the total cooling demand of between 1 and 3%. Furthermore, the construction requirements are for buildings to be energy efficient with regards to thermal insulation, while the aspect of thermal inertia is completely omitted in the regulations [12]. As was revealed in previous papers [13,14], the effect of thermal inertia on the building envelope can significantly change the heat flux by peak shaving under extreme conditions.

One of the most promising technologies in building applications is latent heat storage systems with phase change materials (PCM) [15,16,17]. Different techniques of PCM incorporation in opaque elements were considered in the past. Micro- [18,19] and nano-encapsulation [20], direct application [21,22], shape stabilised [23,24] or mats with pockets [25,26] were investigated experimentally and numerically. Although macro and microencapsulation give flexibility in future applications, the content of PCM is limited by the volume of the additional matrix. A more effective solution considering the amount of PCM in an unit volume is to enclose the pure material in a metal [27,28] or glass [29,30] container. However, considering the daily cycle of heat storage and release as well as the relatively low thermal conductivity of PCM, the thickness of such containers should be limited to a few centimetres, even when it is exposed to direct solar radiation [31].

One of the specific examples of PCM containers is PCM-glazing [32,33], which is characterized by transparent or semi-transparent (translucent) properties. The optical characteristics [34,35], as well as the dynamics of the melting process [36,37], have been investigated in the past. Studies have confirmed that the PCM transmittance changes significantly due to the change of phase. In the case of solid state, the transmittance is very low (at the level of 0.3–0.4 depending on the layer thickness), while, when PCM is liquid, it rises up to 0.75 [35]. Regarding this characteristic, the PCM window can be treated as a solar protection system until the material is in the solid state [38]. Although the optical properties are well known in the solid and liquid states, the intermittent period when the material melts and solidifies is not well described. Moreover, the thermal processes during the change of phase have been defined in a simplified way when the PCM layer is treated as a body of uniform. Heim et al. [36] made an experiment for a triple glazed PCM window irradiated by an artificial sun. It was confirmed that the transmittance of PCM does not change linearly and the melting process in a PCM cavity is more complex, with regions of solid, mushy and melted layers. According to the results from the initial experimental analyses, it was confirmed that the thermal model should consider the nonuniformity of the PCM cavity according to the amount of latent heat stored in the material as well as the temperature distribution in the PCM layer.

The main aim of the presented study is the investigation of the thermal behaviour of triple glazing with a PCM layer in one cavity, as well as the development of a heat transfer model including phase change using the moving mushy volume approach (Section 2). In the proposed approach, the PCM layer is treated as a set of very thin sublayers for which the energy balance equation is solved, simultaneously considering heat transfer with latent heat storage. The proposed model was experimentally validated with the results obtained from the climatic chamber (Section 3). A full-scale, two-section window was developed for the experiment. The experiment was conducted under dynamic conditions from fully solid to fully liquid state (Section 4). The simulation results obtained for the same boundary conditions were compared with the experiment (Section 5).

2. Numerical Model of Heat Transfer

Solving the problem of transient heat transfer via a multi-layered structure demands the application of some numerical approaches due to the fact that the general explicit solution of the partial differential equation has not been found yet. In the presented paper, the authors decided to develop an algorithm based on a control volume method. The choice was driven by its easy applicability in the weak formulation of the extensive value conservation law, where the space and time derivatives are of the same order (Equation (1)); the explanation of the indexes in the equation is presented in Figure 1.

$$\frac{\delta }{\delta \tau }{{\displaystyle \int }}_{{\Omega }_p}^{ }\phi d\Omega -{{\displaystyle \oint }}_{{\Gamma }_p}^{ }\left(k \frac{\delta \phi }{\delta x_j}\right)n_{j}d\Gamma ={{\displaystyle \int }}_{{\Omega }_p}^{ }{Q}_{V}d\Omega$$

(1)

Discretization of space derivatives was performed using a finite difference and one-dimensional model. Despite the fact that such an approach simplifies the problem regarding, e.g., thermal bridges or convection, similar algorithms provided satisfying results presented in other papers, e.g., [39,40]. Time derivative was approximated using the backward Euler method which guarantees unconditional stability (Figure 2b) [41].

The approach to transient heat transfer presented in Equation (1) demands some additional assumptions to simulate the phase change. Different methods were presented in the past (numerical approximation of Dirac’s function peak in [42], [43] or [44], linear simplification of the enthalpy change during melting or solidification in [40,45] or application of the linear simplification of the effective heat capacity [46,47]). In the presented paper, the authors decided to use one of the effective specific heat C_eff(T) functions presented in [48] and described below (Equation (2)) with the corresponding stage of melting function β(T) (Equation (3)).

$$c_{eff}\left(T\right)=c+L · \frac{\sqrt{2} \gamma }{\Delta T \sqrt{\mathsf{\pi }}} · e^{-\frac{2\gamma {\left(T-T_m\right)}^2}{{\Delta T}^2 }}$$

(2)

$$\beta \left(T\right)=0.5·\left[\mathrm{erf}\left(\frac{\sqrt{2}·\gamma ·\left(T-T_m\right)}{\Delta T}\right)+1\right]$$

(3)

Despite the fact that the presented functions are smooth and have no limitations of applicability regarding the temperature range, iterative calculations were needed to achieve better convergence to the experimental results [49]. Using Equation (1) creates a five diagonal matrix which can be efficiently solved explicitly in each iteration using the modified Thomas algorithm (often called the modified tridiagonal matrix algorithm—TDMA, e.g., [50]).

3. Experimental Set-Up

The experimental investigations were carried out in a laboratory scale. Validation of the numerical model was performed based on the results obtained from the climatic chamber (Figure 3a). The dynamic conditions were emulated by temperature changes on one side of the PCM-glazing, while on the other side of the glazing, the conditions were kept on a constant level. The experimental set-up consists of three parts. The first part is two completely thermal guarded chambers. This structure was made of 100 mm polystyrene reinforced by the structural board and steel frame construction. This solution leads to ensured stiffness and airtightness. The second part is the heating/cooling system, which consists of fans and coils. To obtain the assumed temperatures, each section was equipped with a coil with a length of about 45 m each, located in the middle of the chambers. The heating agent in the coil (unit 1) was propylene glycol, and for the second unit coil, ethanol was used. A Julabo (model FP89 HLTK) thermostat was used as a device in unit 2, while a Huber thermostat (model ministat 230) was used in unit 1, the powers of which are shown in

Table 1. Performance values of cooling/heating section.

Temperature	[°C]	20	0	−20	−40
Cooling capacity	[kW] (medium: ethanol)	1.00	0.92	0.88	0.75
Heating capacity		1.30	1.30	1.30	1.30
Cooling capacity	[kW] (medium: glycol)	0.42	0.38	0.25	0.05
Heating capacity		1.50	1.50	1.50	1.50

.

To unify the vertical temperature profiles in each of the chambers, two fans (model YWF-4D-250S) were used, mounted in the lower part of the chamber in the middle of the coils (Figure 3b, Section B). The air stream was directed parallelly to the glazing surface from the bottom to the top. The third part is the temperature and heat flow measuring devices and data acquisition system. Each of the chambers was equipped with 6 Pt100 4-wire sensors, class A according to the standard PN-EN 60751 with an additional sensor included in the Heat Flux Measurement Kit (Green Teg KIT-1583C). The arrangement of the temperature sensors is presented in Figure 3b, Section A. The signals from the Pt100 sensors were collected through a universal 24-bit measuring module and saved on a computer at a frequency of 1 Hz.

The main parameters of the measuring instruments are shown in

Table 2. Main parameters of the experimental measuring instruments.

Parameter	No	Model	Range	Accuracy
Air temperature in chamber	TT (02/5/6)	TP-372	–40… + 400 °C	±(0.15 + 0.002·|T|)
Surface temperature at glass	TT (01/3)	TP-366	–40… + 400 °C	±(0.15 + 0.002·|T|)
Heat flow at glass surface	QR (01/2)	gSkin®	±200 [W/m2]	±3%

.

The experimental structure was a triple glazed window with one cavity filled with PCM and one with argon. Dimensions and physical parameters of all layers are listed in

Table 3. Material parameters and dimensions.

Material	d	c	ρ	k
[-]	[m]	[J/(kg∙K)]	[kg/m3]	[W/(m∙K)]
Glass *	0.0084	840	2500	1.00
PCM	0.0120	2000	880	0.20
Glass	0.0080	840	2500	1.00
Argon	0.0120	520	1.80	0.025
Glass	0.0040	840	2500	1.00

* glass with protective foil 0.4 mm.

and the numerical discretization of the domain is presented in Figure 4. Structure in the experimental set-up needed reinforcement of the glass layers holding the phase change material due to the fact of hydrostatic pressure and possible deformation of glass. Therefore, for the outer layer, the authors chose 8.4 mm thick glass (two layers of 4 mm reinforced by 0.4 mm of PCV protection foil) and the inner layer of glass was 8 mm thick.

During the experiment, the air flow inside both chambers was kept at a constant level. Due to the difficulty of determining the exact speed (v_x, v_y, v_z), the flow rate was determined based on the fan power supply frequency, regulated by the frequency inverter. The experiment described in this article was performed for the frequency of 25 Hz. In the chamber used for mimicking internal conditions, the temperature of 24 °C was kept during the whole experiment. In the chamber used for mimicking the external conditions, the initial temperature was 10 °C and was kept at a steady state between the two chambers along with the full solidification of the PCM, which was confirmed by the data from the heat flux measurement (Figure 5). Subsequently, the temperature was increased until it reached 50 °C. The temperature was kept at the maximum level for a period of 1.5 h. Thereafter, the temperature set point was changed to the initial value. The experiment was terminated after stabilization of the temperature and heat flux in each section of the chamber was at a constant level for 4 h.

4. Model Definition and Boundary Conditions

4.1. Model Definition

While dividing the domain into control volumes, the authors decided to locate the nodes of the inner and outer layers of the glasses on their surfaces to gain a more precise estimation of the conduction coefficient between nodes representing different medias (Figure 4: nodes 1, 4, n − 6, n − 4, n − 2, n).

Phase change material used in the experimental set-up was RT18HC by Rubitherm. The partial enthalpy distribution H for the whole phase change temperature range is presented in (Figure 6), separately for the case of melting and solidification.

The partial enthalpy is shown for specific 1 K temperature ranges. The maximum value for melting is observed from 17.5 to 18.5 °C, while for solidification from 16.5 to 17.5 °C. To perform the selection of the parameters for Equation (2) the following assumptions were taken into account:

-

Parameters T_m, ΔT and γ were selected by minimizing Equation (4)

$$f\left(T,T_m,\Delta T,\gamma \right)={\displaystyle \sum }_{T_i=10}^{T_i=25}(H_R\left(T_i\right)-{{\displaystyle \int }}_{T_i-0,5K}^{T_i+0,5K}{c}_{eff}\left(T,T_m,\Delta T,\gamma \right)dT{)}^2$$

(4)

-

Integral of effective specific heat c_eff(T) was equal to the latent heat declared by Rubitherm L_R = 262 kJ/kg

$${\displaystyle \sum }_{T_i=10}^{T_i=25}{{\displaystyle \int }}_{T_i-0,5K}^{T_i+0,5K}{c}_{eff}\left(T,T_m,\Delta T,\gamma \right)dT=L_R$$

(5)

Optimisation led to an effective heat capacity function in the phase change range presented in Figure 7. The values of partial enthalpy obtained for a specific function (H) are presented in Figure 8 and compared with the enthalpy declared by the producer (H_R).

Due to the symmetric characteristic of the c_eff(T) function, some differences between the declared and modelled parameters are inevitable. However, the total modelled latent heat was optimised according to Equation (5) with a difference of 0.04% in relation to the manufacturer’s data. The maximal error for the specific temperature was no more than 3% of the latent heat with less than 0.5% for the peak value.

4.2. Boundary Conditions

As a boundary condition, the authors adopted the average value of the four temperatures measured around both coils. In the next step, the authors performed a preliminary simulation to set convection coefficients that gave satisfying agreement with the experiment under the condition of stationary heat transfer (time between 300 and 400 min). The authors assumed that due to the fact that both sides of the glass unit convection were forced, despite the different temperature gradients between the coils and the surface, the convective coefficients were similar and in the calculations they were treated as equal. For the frequency of 25 Hz, a satisfying correlation was achieved for α_conv = 14.0 W/m²∙K (Figure 9). Due to the fact that the measurements were performed in the heat chamber, the radiative component of heat transfer was omitted.

5. Results

The result of the experiment was the measured heat flow density on the outer layer of the glass closing the cavity filled with gas (in the model the location is represented by the node n on Figure 5, Equation (6)). The simulation was performed in the domain of temperature, not heat flow, so, to compare the experiment with the calculations, the authors assumed that the heat flow density q between the two control volumes closest in the model to the actual location of the gauge (n − 1 and n—Figure 5) allowed the results comparison.

$$q_{calc.n-1 ÷ n}=\frac{\left(T_n-T_{n-1}\right)·k_{harm.n-1 ÷ n}}{d_{n-1 ÷ n}}$$

(6)

Due to the fact that the chosen methodology of modelling the phase change based on the effective heat capacity c_eff is not convergent by definition (e.g., [43,44]) the authors decided to perform an optimisation in the field of the number of control volumes representing PCM and longitude of the time step dt. Optimisation was performed separately for both time and space by analysing the total error measured according to L² norm for the discrete domain (Equation (7)), and the conditional value of the main matrix of a system of equations defined as a ratio of the highest and lowest positive eigenvalues. The authors found the conditional value of the main matrix as an essential aspect of assessment of the results. Its high values indicate the sensitivity of the equations system to a precision of the input data, which is why for the current state of knowledge about PCM parameters in mushy states this should be treated as a key factor. Due to the fact that the conditional value was different for each time step (changing the physical parameters of PCM) the authors presented a comparison of only the highest values. The first analysed was the number of CV representing PCM. To omit additional rounding up errors 12 mm PCM gap was divided into 3, 4, 6, 8, 9, 12, 16 and 24 CVs.

$$R\left(L^2\right)={\displaystyle \sum }_j{(q_{meas.j}-q_{calc.i})}^2$$

(7)

It can be seen on Figure 10 that, with the increasing number of CV representing PCM, the error increases get closer to the asymptote. This is not a perfect case as, according to Lax’s law, the error should decrease to zero [51], but the presented model is not analysing all physical processes taking place in the structure (thermal bridges on the edges of the glasses, 3D character of the heat transfer, etc.) and the asymptote presents the sum of errors that is not possible to be omitted with applied simplifications. Based on Figure 8, the authors assumed that for more than 8 CVs, the total square error is close enough to the asymptote. At the same time, the conditional value presented a minimum for CVs numbers between 6 and 12. It is interesting that for 16 and 24 CVs representing PCM, the maximal conditional value was increasing, reaching a higher value than for 3 CVs. This means that in such an approach to modelling of the phase change phenomenon (using effective specific heat), the compaction of the mesh does not always provide a better solution. For the analysis of the optimal time step, the authors used 12 control volumes representing 12 mm of phase change material. In such a case, the domain discretization presented in Figure 4 is as presented in Figure 11. In the next step, optimisation of the longitude of time step dt was performed in the range from 1 min to 10 min.

Both the total error and the maximal conditional value presented as minimum in relation to the time step, which is very interesting because it proves that the field of time domain compaction should also not be performed without further analysis. This is essential for the choice of the time domain discretization method because not all are unconditionally stable. For example, the forward Euler method could demand a very short time step due to the stability condition, which could possibly result in a bigger error. Time steps of 5 min and 6 min present very similar results and the authors decided to present the remaining results for dt = 5 min (Figure 12).

Comparison of the simulation (q_calc) and experiment results (q_meas) were presented only since the stationary heat flow started (t > 300 min) (Figure 13).

Heat flux measured in the experiment represents several stages and mechanisms of heat transfer via structure:

• 300 min < t < ~400 min—stationary heat flow with temperatures in PCM below the phase change range (compare to Figure 14 where all the β ≈ 0)
• ~400 min < t < ~550 min—transient heat flow, the structure heating up but the temperatures in PCM are below the phase change range
• ~550 min < t < ~800 min—temperatures in PCM are in phase change range which causes melting in CVs 5–16 (compare to Figure 14 where 0 < β < 1)
• ~800 min < t < ~900 min—transient heat flow causes the heating up of the structure while PCM temperatures are over the phase change range (compare to Figure 14 where all the β ≈ 1)
• ~900 min < t < ~1200 min—transient heat flow is cooling down the structure, temperatures in PCM are getting close to the phase change range, but material is still fully liquid (compare to Figure 14 where all the β ≈ 1)
• t > ~1200 min—solidifying of the PCM in CV 5–16 begins when temperatures in PCM are entering the phase change range (compare to Figure 14 where 0 < β < 1)

Because the parameters in Equation (2) were selected for the case of melting (Figure 6 and Figure 8), further consideration was given mostly for the period between 300 min and 1200 min. However, despite that, the experiment also covered stationary heat transfer in the solid state, transient heat transfer in the liquid state, and the beginning of the solidification. Such an approach was very important for the authors as the long-term simulation of the heat transfer via a structure with PCM incorporated would involve all listed mechanisms. From the modelling point of view, the mushy states of the PCM are very difficult. This is due to the fact that their physical parameters are still unexplored, and the physical phenomena occurring in them go far beyond the conduction itself. However, despite the fact that the differences between the simulation and the experiment are most significant in the melting time period (~550 min < t < ~800 min) during the whole simulation, the error did not significantly affect the conclusions that were stated based on the simulation alone. This proves that it could be sufficient for assessing whether the PCM improves the energy efficiency of the structure or not without performing additional experiments. This is essential for the choice of the PCM with optimal phase change temperature ranges, which would demand many difficult and expensive experiments.

The stage of melting of each control volume representing PCM is measured by the β parameter (Equation (3)). The authors decided to present β5–β16 along with the average of them (Figure 14).

It can be easily seen in Figure 14 that in the presented experiment the melting starts from node 5 and moves to node 16 but, due to the wide range of melting temperatures (Figure 6), the melting in the following volumes starts before it ends in the previous. This means that from approximately 500 min to 800 min the whole PCM layer is melting but is not fully solid or fully liquid, which then means that, until the last volume does not reach the highest temperature of melting range (25 °C), the measured flux cannot change, although the experiment proved different (600 < t < 800 min in Figure 11). Such phenomenon is less important in the pure conduction problem, while the thermal conductivity of PCM does not vary significantly in the range of melting, but is crucial in the problem of solar radiation propagation, which was not included in the presented experiment, but is the basic aim of applying PCM into transparent and translucent structures.

6. Discussion

Energy storage for improving building energy performance has been studied in a variety of applications and with different charging and discharging mechanisms. Extended analysis is mostly required in applications where charging takes place under the influence of weather conditions. Examples of such solutions are PCM materials embodied in external walls of buildings or transparent partitions. Assessment of their impact on the building’s energy efficiency requires complex measurements or can be carried out using heat transfer simulations.

Examples of such simulations can be found in [46] or [48]. In [46] the results were obtained with the use of a proprietary computational algorithm based on balancing the energy in each node at each time step. The presented discretization of the mathematical problem suggests an analogy to electrical systems, which most likely requires iterative calculations. The model includes the impact of the accumulation of solar radiation energy as well as radiation to the sky. The phase change was modelled assuming a piecewise linear function of effective specific heat. The use of such conditional functions usually complicates the algorithm, which may be significant for computing time in modelling complex partitions or entire buildings, but as it was presented in [52] it doesn’t have a significant impact on the accuracy of the simulation. Based on the experiment, the model was calibrated in terms of the optical parameters, but the presented results were obtained for one type of the mesh and the longitude of time step. Analyses presented in this paper show that both the mesh size and time step are essential regarding the accuracy of the simulation measured according to the L² norm or conditional value of the matrix. While the phase change problem solved using the effective heat capacity function is not convergent by definition, the results presented in Figure 10 and Figure 12 prove that it is not obvious that higher compaction of the mesh or time steps provides better results.

In [48] the simulation was carried out using the commonly available code Modelica, which allows the simulation of single partitions as well as entire buildings. The phase change was simulated using the three functions of effective specific heat, which were verified by modelling the Stefan problem, and then validated on the basis of the obtained results of experimental studies. All three functions showed a satisfactory compliance of the simulation with the explicit solution of the Stefan problem, and this is why the authors of the presented paper chose one of them in their simulations (Equation (2)). The use of commercial codes such as EnergyPlus, ESP-r, TRNSys, or as in [48] Modellica has a number of advantages. One of them is the high probability that extensive testing of the algorithm’s has been performed by its authors. This is especially important in the case of methods based on simplification such as analogy to electrical systems, because the author of the code must take care of its stability and compliance, much more carefully than in the case of numerical methods such as FDM, FEM or that used by the authors of this paper, CVM, widely tested in terms of, e.g., stability of time derivative discretization. Additionally, while comparing the simulation results that were not obtained by solving numerically the systems of partial differential equations with the experiment (as in [46] or [48]), special attention should be paid to what the calculation results finally represent (e.g., heat flux density on the wall surface, average heat flux density in the layer, material/partition, etc.) as this may provide an additional view on the causes of any discrepancies.

$$RMSE=\sqrt{\frac{1}{j} · {\displaystyle \sum }_{j=1}^t{\left(e_j-s_j\right)}^2}$$

(8)

The most sophisticated energy transfer mechanism among [46,47,48] and this paper was modelled in [46]. In addition to heat transfer, it took into account the absorption of solar radiation energy in the subsequent layers, which had a key impact on the phase change in PCM. The RMSE (Equation (8)) of heat flux density obtained in [46] was 14.9 W/m² average, with 11.1 W/m² for the winter period and 17.9 W/m² for the summer period. Similar partitions (a two-chamber window in which one of the voids was filled with PCM and the other with gas) were modelled in the presented paper; however, due to the experiment being conducted in a climate chamber, the components related to solar radiation absorption and radiation to the sky did not participate in the calculations. The RMSE of heat flux density obtained by the authors for the simulation presented in Figure 11 was 0.9 W/m². In [48], the results for heat transfer via an opaque partition were tested in a test room without taking into account solar radiation, depending on the location of the element containing PCM within the cross section of the structure the RMSE of heat flux density ranged from 0.34 W/m² to 5.93 W/m². Due to the different nature of the simulated energy transfer mechanisms, the RMSE values cannot be directly compared, but all results show that the algorithms are sufficiently accurate for the initial assessment of the energy storage embodied into the partition, despite the very different approach to the simulations.

7. Conclusions

In the paper, the authors proposed a numerical model based on the control volume method and using the moving mushy volume approach. Discretization of space derivatives was performed using a finite difference and one-dimensional model. The proposed model is dedicated to solving heat transfer phenomena including the change of phase solid/liquid/solid in a thin construction containing PCM.

The obtained results of the heat flux showed all stages of the phase transition. Based on the simulation, it was observed that until the last volume does not reach the highest temperature of melting range, the measured flux does not change, although the experiment proved a different behaviour of the PCM layer under investigation showing a slightly decrease in heat flux. This should be a subject for further analysis as well as incorporation of the solar energy accumulation into energy balance. The level of heat stored in a single volume or in the whole PCM layer was estimated by the stage of melting function β, which can be useful for estimating the level of charging/discharging of the individual control volume.

The satisfied agreement between simulation and experiment were obtained under the condition of stationary heat transfer with convective surface coefficient 14 W/(m²⋅K). The optimised magnitude of the single control volume of PCM layer was 1 mm and the longitude of the time step was 5 min. Due to the results from the real scale laboratory experiment, the proposed model was fully validated with the satisfied value of RMSE for the heat flux of the level on 0.9 W/m².