The Influence of Hydrodearomatisation Reaction Kinetics on the Modelling of Sulphur and Aromatics Removal from Diesel Fuel in an Industrial Hydrotreating Process
Abstract
:1. Introduction
2. Experimental Part
2.1. Industrial Test Run Data
2.2. The Reactor Model
2.3. Hydrodearomatisation Reactions
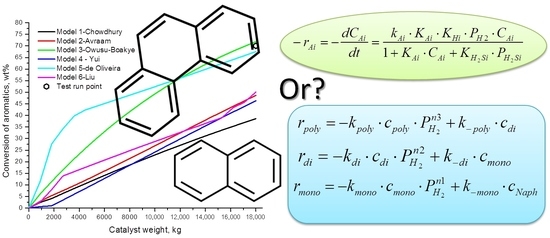
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| T | temperature, K |
| P | pressure, bar |
| Ki | vaur–liquid equilibrium constant for component i |
| FL/FV | liquid-to-vapour molar flow ratio |
| Cp | heat capacity, kJ/mol/K |
| f | catalyst wetting efficiency |
| Re | Reynolds number |
| ΔP | pressure drop, Pa/m |
| g | gravitational acceleration, m/s2 |
| Ga | Galileo number |
| dp | equivalent particle diameter, m |
| W | catalyst weight, kg |
| Ci | molar concentration of component i in liquid phase, kmol/m3 |
| ri | reaction rate for component i, kmol/kgcat/h |
| ki, σ/τ | kinetic parameter for component i, kmol/kgcat/h |
| Ki,σ/τ | kinetic adsorption parameter for component i, m3/kmol |
| DEN σ/τ | overall adsorption parameter |
| H | enthalpy, kJ/kmol |
| . | effective diffusivity for component i, m2/s |
| DAB,i | molecular diffusivity for component i, m2/s |
| DK,i | Knudsen diffusivity for component i, m2/s |
| kiAPPI | pseudo first-order kinetic constant for component i |
| kgi | gas phase external mass transfer coefficient for component i, m/s |
| kli | liquid phase external mass transfer coefficient for component i, m/s |
| X | Lockhart–Martinelli number |
| We | Weber number |
| Sc | Schmidt number |
| Subscripts: | |
| i | component i |
| BT | benzothiophene |
| DBT1 | methyldibenzothiophene |
| DBT2 | dimethyldibenzothiophene |
| DBT3 | trimethyldibenzothiophene |
| H2 | hydrogen |
| H2S | hydrogen sulphide |
| Superscripts: | |
| L | liquid |
| V | vapour |
| Greek symbols: | |
| ρ | density, kmol/m3 |
| Ωi | overall effectiveness factor |
| ηi | internal effectiveness factor |
| Φi | Thiele modulus |
| ε | porosity of the catalyst particle |
| εb | porosity of the catalyst bed |
| ρp | density of the catalyst pellet, kg/m3 |
References
- Hayashida, K.; Haji, K. Effects of Fuel Properties on Diffusion Combustion and Deposit Accumulation, Fossil Fuel and the Environment; Khan, S., Ed.; IntechOpen: London, UK, 2012; pp. 1–18. ISBN 978-953-51-0277-9. Available online: https://www.intechopen.com/books/fossil-fuel-and-the-environment/effects-of-fuel-properties-on-diffusion-combustion-and-deposit-accumulation (accessed on 20 June 2021).
- Ghosh, P.; Jaffe, S.B. Detailed composition-based model for predicting the cetane number of diesel fuels. Ind. Eng. Chem. Res. 2006, 45, 346–351. [Google Scholar] [CrossRef]
- Kidoguchi, Y.; Yang, C.; Miwa, K. Effects of Fuel Properties on Combustion and Emission Characteristics of a Direct-Injection Diesel Engine. J. Fuels Lubr. 2000, 109, 1149–1157. Available online: www.jstor.org/stable/44745922 (accessed on 8 June 2021).
- Danaher, W.J.; Palmer, L.D. Chemical changes and ignition quality improvement resulting from hydrotreating light cycle oil. Fuel 1988, 67, 1441–1445. [Google Scholar] [CrossRef]
- Quality of Petrol and Diesel Fuel Used for Road Transport in the European Union, Report from the Commission to The European Parliament and the Council; 23.3.2012 COM(2012) 127 Final; European Commission: Belgium, Brussels, 2012; Available online: https://data.consilium.europa.eu/doc/document/ST-8168-2012-INIT/en/pdf (accessed on 20 June 2021).
- Mijatovic, I.M.; Glisic, S.B.; Orlovic, A.M. Modelling a catalytic reactor for hydrotreating of straight-run gas oil blended with FCC naphtha and light cycle oil: The influence of vapour-liquid equilibrium. Ind. Eng. Chem. Res. 2014, 53, 19104–19116. [Google Scholar] [CrossRef]
- Dukanović, Z.; Glišić, S.B.; Čobanin, V.J.; Nićiforović, M.; Georgiou, C.A.; Orlović, A.M. Hydrotreating of straight-run gas oil blended with FCC naphtha and light cycle oil. Fuel Process. Technol. 2013, 106, 160–165. [Google Scholar] [CrossRef]
- Anchyeta, J. Modeling and Simulation of Catalytic Reactors for Petroleum Refining, 1st ed.; John Wiley & Sons: New York, NY, USA, 2011; ISBN 978-0-470-18530-8. [Google Scholar]
- Chen, J.; Mulgundmath, V.; Wang, N. Accounting for Vapor-Liquid Equilibrium in the Modeling and Simulation of a Commercial Hydrotreating Reactor. Ind. Eng. Chem. Res. 2011, 50, 1571–1579. [Google Scholar] [CrossRef]
- Girgis, M.J.; Gates, B.C. Reactivities, reaction networks, and kinetics in high pressure catalytic hydroprocessing. Ind. Eng. Chem. Res. 1991, 30, 2021–2058. [Google Scholar] [CrossRef]
- Stanislaus, A.; Cooper, B.H. Aromatic hydrogenation catalysis: A review. Catal Rev. 1994, 36, 75–123. [Google Scholar] [CrossRef]
- Korre, S.C.; Klein, M.T.; Quann, R.J. Polynuclear aromatic hydrocarbons hydrogenation. 1. Experimental reaction pathways and kinetics. Ind. Eng. Chem. Res. 1995, 34, 101–117. [Google Scholar] [CrossRef]
- Korre, S.C.; Neurock, M.; Klein, M.T.; Quann, R.J. Hydrogenation of polynuclear aromatic hydrocarbons. 2. Quantitative structure/reactivity correlations. Chem. Eng. Sci. 1994, 49, 4191–4210. [Google Scholar] [CrossRef]
- Chowdhury, R.; Pedernera, E.; Reimert, R. Trickle-Bed Reactor Model for Desulfurization and Dearomatization of Diesel. AIChE J. 2002, 48, 126–135. [Google Scholar] [CrossRef]
- Wilson, M.F.; Kriz, J.F. Upgrading of Middle Distillate Fractions of a Syncrude from Athabasca Oil Sands. Fuel 1984, 63, 190–196. [Google Scholar] [CrossRef]
- Bhaskar, M.; Valavarasu, G.; Sairam, B.; Balaraman, K.S.; Balu, K. Three-Phase Reactor Model to Simulate the Performance of Pilot-Plant and Industrial Trickle-Bed Reactors Sustaining Hydrotreating Reactions. Ind. Eng. Chem. Res. 2004, 43, 6654–6669. [Google Scholar] [CrossRef]
- Gunjal, P.R.; Ranade, V.V. Modeling of laboratory and commercial scale hydro-processing reactors using CFD. Chem. Eng. Sci. 2007, 62, 5512–5526. [Google Scholar] [CrossRef]
- Mederos, F.S.; Ancheyta, J.; Elizalde, I. Dynamic modeling and simulation of hydrotreating of gas oil obtained from heavy crude oil. Appl. Catal. A Gen. 2012, 425-426, 13–27. [Google Scholar] [CrossRef]
- Avraam, D.G.; Vasalos, I.A. HdPro: A mathematical model of trickle-bed reactors for the catalytic hydroprocessing of oil feedstocks. Catal. Today 2003, 79–80, 275–283. [Google Scholar] [CrossRef]
- Jiménez, F.; Kafarov, V.; Nuňez, M. Modeling of industrial reactor for hydrotreating of vacuum gas oils—Simultaneous hydrodesulfurization, hydrodenitrogenation and hydrodearomatization reactions. Chem. Eng. J. 2007, 134, 200–208. [Google Scholar] [CrossRef]
- Jiménez, F.; Nuňez, M.; Kafarov, V. Study and modeling of simultaneous hydrodesulfurization, hydrodenitrogenation and hydrodearomatization on vacuum gas oil hydrotreatment. Comput. Aided Chem. Eng. 2005, 20, 619–624. [Google Scholar]
- Owusu-Boakye, A.; Dalai, A.K.; Ferdous, D.; Adjaye, J. Experimental and Kinetics Studies of Aromatic Hydrogenation in a Two-Stage Hydrotreating Process using NiMo/Al2O3 and NiW/Al2O3 Catalysts. Can. J. Chem Eng. 2006, 84, 572–580. [Google Scholar] [CrossRef]
- Yui, S.M.; Sanford, E.C. Kinetics of aromatics hydrogenation and prediction of cetane number of synthetic distillates, Proceedings—Refining Department. In Proceedings of the 50th Midyear Meeting, Kansas City, MO, USA, 13–16 May 1985; American Petroleum Institute: Washington, DC, USA, 1985; pp. 290–297. [Google Scholar]
- De Oliveira, L.P.; Verstraete, J.J.; Kolb, M. A Monte Carlo modeling methodology for the simulation of hydrotreating processes. Chem Eng. J. 2012, 207–208, 94–102. [Google Scholar] [CrossRef]
- Liu, Z.; Zheng, Y.; Wang, W.; Zhang, Q.; Jia, L. Simulation of hydrotreating of light cycle oil with a system dynamics model. Appl. Catal. A Gen. 2008, 339, 209–220. [Google Scholar] [CrossRef]
- Magnabosco, L.M. A mathematical model for cataytic hydrogenation of aromatics in petroleum refining feedstocks. Stud. Surf. Sci. Catal. 1989, 53, 481–496, ISBN 9780080887005. [Google Scholar]
- Cheng, Z.; Fang, X.; Zeng, R.; Han, B.; Huang, L.; Yuan, W. Deep removal of sulfur and aromatics from diesel through two-stage concurrently and counter currently operated fixed-bed reactors. Chem. Eng. Sci. 2004, 59, 5465–5472. [Google Scholar] [CrossRef]
- Papadias, D.; Edsberg, L.; Bjornbom, P. Simplifed method for effectiveness factor calculations in irregular geometries of washcoats. Chem. Eng. Sci. 2000, 55, 1447–1459. [Google Scholar] [CrossRef]
- Sie, S.T.; Krishna, R. Process development and scale up: III. Scale-up and scale-down of trickle bed processes. Rev. Chem. Eng. 1998, 14, 203–252. [Google Scholar] [CrossRef]
- Cheng, Z.-M.; Anter, A.M.; Yuan, W.-K. Intensification of phase transition on multiphase reactions. AIChE J. 2001, 47, 1185–1192. [Google Scholar] [CrossRef]
- Cheng, Z.-M.; Zhou, Z.-M.; Yuan, W.-K. Determination of catalyst wetting fraction on the molecular level. AIChE J. 2007, 53, 741–745. [Google Scholar] [CrossRef]
- Cheng, Z.M.; Anter, A.M.; Fang, X.C.; Xiao, Q.; Yuan, W.K.; Bhatia, S.K. Dryout phenomena in a three-phase fixed-bed reactor. AIChE J. 2003, 49, 225–231. [Google Scholar] [CrossRef]
- Naranov, E.R.; Maximova, A.L. Selective conversion of aromatics into cis-isomers of naphthenes using Ru catalysts based on the supports of different nature. Catal. Today 2019, 329, 94–101. [Google Scholar] [CrossRef]
- Ramírez-Castelán, C.E.; Hidalgo-Vivas, A.; Brix, J.; Jensen, A.D.; Huusom, J.K. Mathematical modelling and simulation of a trickle-bed reactor for hydrotreating of petroleum feedstock. Int. J. Chem. React. Eng. 2019, 17, 20180176. [Google Scholar] [CrossRef] [Green Version]
- Neto, A.T.P.; Fernandes, T.C.R.L.; Silva, H.B., Jr.; de Araújo, A.C.B.; Alves, J.J.N. Three-phase trickle-bed reactor model for industrial hydrotreating processes: CFD and experimental verification. Fuel Process. Technol. 2020, 208, 106496. [Google Scholar] [CrossRef]
- Palos, R.; Kekäläinen, T.; Duodu, F.; Gutiérrez, A.; Arandes, J.M.; Jänis, J.; Castañoa, P. Screening hydrotreating catalysts for the valorization of a light cycle oil/scrap tires oil blend based on a detailed product analysis. Appl. Catal. B Environ. 2019, 256, 117863. [Google Scholar] [CrossRef]
- Palos, R.; Kekäläinen, T.; Duodu, F.; Gutiérrez, A.; Arandes, J.M.; Jänis, J.; Castaño, P. Detailed nature of tire pyrolysis oil blended with light cycle oil and its hydroprocessed products using a NiW/HY catalyst. Waste Manag. 2021, 128, 36–44. [Google Scholar] [CrossRef] [PubMed]




| Parameter | Inlet Stream | Outlet Stream | |
|---|---|---|---|
| Straight Run Gas Oil | Fluid Catalytic Cracking Naphtha and Light Cycle Oil | Hydrotreated Gas Oil | |
| Distillation range, °C | 33–335 | ||
| Sulphur content, % wt. | 0.7305 | 1.1400 | |
| Thiol/mercaptan sulphur, % wt. | 0.0162 | 0.0271 | 0 |
| Paraffin and naphthenic content, % vol. | 68.7 | 32.1 | 73.0 |
| Olefins content, % vol. | 5.2 | 16.9 | 0 |
| Aromatics content, % vol. | 26.1 | 51.0 | 27.0 |
| Monoaromatic content, % wt. | 19.4 | 10.9 | 27.4 |
| Diaromatic content, % wt. | 11.5 | 5.1 | 4.6 |
| Triaromatic content, % wt. | 1.41 | 16.0 | 0.70 |
| Parameter: | Equation: |
|---|---|
| Equilibrium constants | ; i = pseudocomponent |
| Liquid-to-vapour flow ratios | |
| Densities of the vapour and liquid phases | |
| Heat capacities | |
| Catalyst wetting efficiency | |
| Overall catalyst effectiveness; the internal effectiveness factor; generalized Thiele modulus | ; ; where i = BT, DBT1, DBT2, DBT3, and A1, f = phase (liquid or vapour) |
| Material balance equations for reacting components in the process of hydrodesulphurisation: BT, DBT1, DBT2, and DBT3 | ; |
| Material balance equations for reacting components in the process of hydrodearomatisation | ; |
| The overall energy balance |
| Model | Ref. | Catalyst | Pressure, Temperature, and Gas/Diesel Fraction Ratio | Kinetic Expressions | Stoichiometric Equations |
|---|---|---|---|---|---|
| Model 1 Chowdhury | [14,15] | NiMo/Al2O3 | 2–8 MPa 300–380 °C 100–500 m3(NTP)/m3 | ||
| [16] | NiMo/Al2O3 | 4 MPa 320–360 °C 200 L/L | |||
| [17] | - | 20–80 MPa 320–380 °C 100–500 m3/m3 | |||
| [18] | CoMo/Al2O3 | 5.3 MPa 340–380 °C 356 std m3/m3 | |||
| [26] | W-Mo-Ni-Co/Al2O3 Ni-Mo/Al2O3 | 6.5 MPa 350–360 °C | |||
| Model 2 Avraam | [19,20] | CoMo/&-Al2O3 | 3–7 MPa 350–390 °C 0.1–3 Nm3/m | ||
| [21] | NiMo/Al2O3 | 6–10 MPa 330–390 °C Ratio = 4.5–6.25 | |||
| Model 3 Owusu-Boakye | [22] | NiMo/Al2O3 NiW/Al2O3 | 11.0 MPa 350–390 °C 550 mL/ml | ||
| Model 4 Yui | [23] | NiMo/Al2O3 | 5.8 Mpa 380 °C 2000 (scf/Bbl) | ||
| Model 5 de Oliveira | [24] | CoMo/Al2O3NiMo/Al2O3 | 7.0 MPa (H2) 320 °C | Hydrogenation of an aromatic ring Dehydrogenation of a saturated ring | |
| Model 6 Liu | [25] | - | 7.1 MPa 350 °C 1000 NL/L |
| Model | Kinetic Constant | Ea, kJ/mol | Value |
|---|---|---|---|
| Model 1 Chowdhury | k*poly, s−1 k*di, s−1 k*mono, s−1 | 64 | 5.9 × 10−5 2.8 × 10−5 2.8 × 10−5 |
| Model 2 Avraam | kH, s−1 kD, s−1 | 180 | 1.2 × 10−1 2.1 × 10−2 |
| Model 3 Owusu-Boakye | kA, s−1 KA KH2 KH2S | 85 | 8.7 × 10−3 1.3 × 10−5 2.5 × 10−2 1.3 × 10−5 |
| Model 4 Yui | kf kr | 255 | 3.9 × 10−6 7.6 × 10−7 |
| Model 5 de Oliveira | ksr, kmol kg−1 s−1 Kads, m3 kmol−3 keq, m3 kmol−3 | 51 | 2.2 × 10−5 1.5 × 10−5 5.9 × 10−8 |
| Model 6 Liu | k1, s−1 k2, s−1 k3, s−1 k4, s−1 | 125 | 1.5 × 10−4 1.7 × 10−4 1.5 × 10−4 1.9 × 10−4 |
| Model | ΔT in Reactor, K | Deviation from the Experimental Value, % | Overall Sulphur Conversion, mass% | Deviation from the Experimental Value, % | Aromatics Conversion, mass% | Deviation from the Experimental Value, % |
|---|---|---|---|---|---|---|
| Model 1 Chowdhury | 10.1 | 12.08 | 99.61 | 0.12 | 38.60 | 31.40 |
| Model 2 Avraam | 16.8 | 46.08 | 98.6 | 0.89 | 48.62 | 53.84 |
| Model 3 Owusu-Boakye | 11.4 | 0.87 | 99.41 | 0.01 | 71.80 | 2.57 |
| Model 4 Yui | 20.9 | 81.74 | 99.80 | 0.31 | 46.30 | 33.86 |
| Model 5 de Oliveira | 8.8 | 23.5 | 99.74 | 0.25 | 68.34 | 2.37 |
| Model 6 Liu | 15.9 | 38.26 | 97.70 | 1.80 | 52.07 | 25.62 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Glišić, S.B.; Orlović, A.M. The Influence of Hydrodearomatisation Reaction Kinetics on the Modelling of Sulphur and Aromatics Removal from Diesel Fuel in an Industrial Hydrotreating Process. Energies 2021, 14, 4616. https://doi.org/10.3390/en14154616
Glišić SB, Orlović AM. The Influence of Hydrodearomatisation Reaction Kinetics on the Modelling of Sulphur and Aromatics Removal from Diesel Fuel in an Industrial Hydrotreating Process. Energies. 2021; 14(15):4616. https://doi.org/10.3390/en14154616
Chicago/Turabian StyleGlišić, Sandra B., and Aleksandar M. Orlović. 2021. "The Influence of Hydrodearomatisation Reaction Kinetics on the Modelling of Sulphur and Aromatics Removal from Diesel Fuel in an Industrial Hydrotreating Process" Energies 14, no. 15: 4616. https://doi.org/10.3390/en14154616
APA StyleGlišić, S. B., & Orlović, A. M. (2021). The Influence of Hydrodearomatisation Reaction Kinetics on the Modelling of Sulphur and Aromatics Removal from Diesel Fuel in an Industrial Hydrotreating Process. Energies, 14(15), 4616. https://doi.org/10.3390/en14154616