Shrinking-Core Model Integrating to the Fluid-Dynamic Analysis of Fixed-Bed Adsorption Towers for H2S Removal from Natural Gas
Abstract
:1. Introduction
2. Reactivity Model Development
- The solid sorbent is iron oxide-based [17,18], with known physical and chemical characteristics (adsorption capacity , particle diameter , sphericity , bed void fraction , and bed density . The adsorption capacity refers to the H2S amount that the solid sorbent can remove, i.e., the maximum ratio H2S quantity that the total mass of the sorbent can retain. The H2S composition in the sour gas and the solid sorbent adsorption capacity determine the total amount of sorbent required in an adsorption tower to meet H2S composition in the sweet gas stream.
- The reactivity between hydrogen sulfide and solid sorbent is modeled, taking as a reference the chemical reaction (2) of the hematite (Fe2O3) structure, with the formation of iron sulfide (Fe2S3) and water as reaction products. It is well- known that the hematite structure has a significant affinity to react with H2S. The reaction can occur at room temperature, and it also can be reversible. Due to these characteristics, hematite is commonly used to formulate iron oxide-based solid sorbents for H2S removal [28,29].
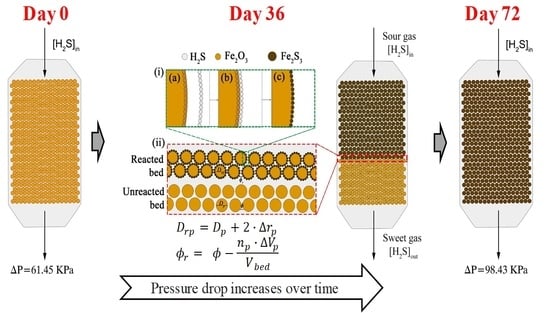
- The shrinking-core model is considered to describe the formation of an iron sulfide monolayer at the solid particles’ external skin. It is considered to be distributed evenly over the entire surface of the particles. As a result of the layer formation, there are changes in the particle diameter and the bed void fraction of the solid sorbent [13,17,30].
- The reaction water keeps the solid sorbent moist. The produced water favors the H2S removal process since it serves as a vehicle for the acid gas dissolution on the solid sorbent surface, promoting its interaction and chemical reaction with the iron oxides [31].
- The chemical reaction inside the fixed-bed adsorption tower is given by packing sections that progressively become saturated. That is to say, the bed wears out one section at a time (adsorption front).
2.1. Volume Variation in the Particles of Solid Sorbents
2.2. Particle Diameter Variation Calculation
2.3. Bed Void Fraction Changing Calculation
2.4. Integration of the Reactivity Model to the Fluid-Dynamic Analysis
- Reacted bed zone: the reaction between the natural gas and the solid sorbent is already considered to have been carried out. Therefore, the Ergun equation calculations consider:
- ○
- The particle diameter and the bed void fraction are calculated using Equations (13) and (18), respectively.
- ○
- The H2S concentration in the natural gas stream remain the same in comparison to the input since no chemical reaction occurs in the reacted bed zone.
- Adsorption front: in this tower zone, the H2S removal takes place. The calculations consider the following aspects:
- ○
- The H2S moles are reduced to the natural gas output specification .
- ○
- The H2S removed from natural gas is calculated using Equation (19).
- ○
- The change in pressure drop is entirely due to the fact that the natural gas moles decrease by the chemical reaction between the H2S and the solid sorbent. The pressure drop is calculated from the Peng–Robinson equation of state [26] by:where is the compressibility factor.
- Unreacted bed zone: it is contemplated that the reaction between the gas and the solid has not yet occurred. Therefore, the Ergun equation calculations consider:
- ○
- The particle diameter and the bed void fraction remain at the initial values for the solid sorbent.
- ○
- The H2S moles remain constant to the output specifications.
2.5. Complementary Calculations
- Repositioning time: refers to the time (expressed in days) required to spend out the fixed bed within the H2S adsorption towers, requiring the replacement or regeneration of the sorbent. The repositioning time is calculated from the total amount of H2S removed from the gas phase and the H2S mass flowrate using the following equation:where:
- Absorption front height: at a given time , the adsorption front height is calculated as:where is the fixed-bed total height.
- Percent variability: for statistical purposes, the variability from the original solid sorbent properties in particle size increase and in bed void fraction decrease are calculated using Equations (24) and (25), respectively.
3. Methods
4. Results and Discussion
4.1. Base Case Analysis
4.2. Validation: Laboratory-Scale and Large-Scale
4.3. Case Studies
5. Summary and Conclusions
- Design and formulate new solid sorbents at laboratory-scale testing, e.g., determining the solid sorbent’s physical properties that establish the best compromise between a high H2S reactivity and a low-pressure drop-in fluid-dynamic tests).
- Analyze adsorption towers already installed at the large scale, e.g., identifying operational problems, such as higher or lower pressure drop values than expected.
- Help plan maintenance operations., e.g., solid sorbent replacement frequency or solid sorbent quantity required.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| cell parameters (Å) | |
| solid sorbent adsorption capacity | |
| surface area of an individual solid particle | |
| methane | |
| fixed-bed diameter | |
| solid sorbent particle diameter | |
| solid sorbent particle diameter in the reacted bed | |
| fixed-bed height differential | |
| ratio of volume variation | |
| natural gas mass velocity per cross-section area () | |
| adsorption front height | |
| inlet H2S concentration | |
| outlet H2S concentration | |
| fixed-bed total height | |
| mass of an individual solid particle | |
| H2S mass flowrate bed | |
| H2S mass adsorbed per individual solid particle | |
| H2S total mass adsorbed | |
| hematite molecular weight | |
| H2S molecular weight | |
| solid particles total number | |
| natural gas pressure | |
| natural gas flowrate | |
| temperature | |
| time | |
| repositioning time | |
| hematite unit cell volume | |
| iron sulfide unit cell volume | |
| fix-bed volume | |
| volume of an individual solid particle | |
| molar volume | |
| total volume of particles in reacted bed | |
| volume of an individual particle in unreacted bed | |
| volume of an individual particle in reacted bed | |
| total volume of particles in unreacted bed | |
| fixed-bed volume | |
| natural gas composition | |
| fixed-bed height | |
| compressibility factor | |
| Greek symbols | |
| particle size increase | |
| bed void fraction decrease | |
| H2S removed from natural gas | |
| pressure drop | |
| pressure drop per fixed-bed height | |
| pressure drop due to the chemical reaction | |
| solid particle radius variation | |
| solid particle volume variation | |
| μ | natural gas viscosity |
| ρ | natural gas density |
| hematite density | |
| fixed-bed density | |
| bed void fraction in unreacted bed | |
| bed void fraction in reacted bed | |
| φ | solid sorbent sphericity |
References
- Ricaurte, M.; Fernández, J.; Viloria, A. An improved method for calculating critical temperatures and critical pressures in natural gas mixtures with up to nC11 hydrocarbons. Oil Gas Sci. Technol. Rev. IFP Energ. Nouv. 2019, 74, 53. [Google Scholar] [CrossRef] [Green Version]
- Ayala, L.; Morgan, E. Natural gas production engineering. In Exploration and Production of Petroleum and Natural Gas, 17th ed.; Riazi, M., Ed.; ASTM International: West Conshohocken, PA, USA, 2016; pp. 395–428. [Google Scholar] [CrossRef]
- Bahadori, A. Natural Gas Processing. Technology and Engineering Design, 1st ed.; Gulf Professional Publishing: Waltham, MA, USA, 2014; pp. 483–546. [Google Scholar] [CrossRef]
- Kohl, A.; Nielsen, R. Chapter 2–Alkanolamines for hydrogen sulfide and carbon dioxide removal. In Gas Purification, 5th ed.; Gulf Professional Publishing: Houston, TX, USA, 1997; pp. 40–186. [Google Scholar] [CrossRef]
- Gupta, M.; Sukanandan, J.; Singh, V.; Pawar, A.; Deuri, B. A holistic approach for mitigation of H2S from crude oil and gas in an offshore/remote environment. In Proceedings of the SPE Oil and Gas India Conference and Exhibition, Mumbai, India, 9–11 April 2019. [Google Scholar] [CrossRef]
- Pollitt, I.; Conde, J. Novel approaches to sour gas treatment in oil and gas—Onshore and offshore facilities. In Proceedings of the Abu Dhabi International Petroleum Exhibition & Conference, Abu Dhabi, UAE, 12–15 November 2018. [Google Scholar] [CrossRef]
- Mokhatab, S.; Poe, W.; Mak, J. Chapter 8–Sulfur recovery and handling. In Handbook of Natural Gas Transmission and Processing, 4th ed.; Gulf Professional Publishing: Cambridge, MA, USA, 2019; pp. 271–305. [Google Scholar] [CrossRef]
- Ahmad, W.; Sethupathi, S.; Kanadasan, G.; Lau, L.; Kanthasamy, R. A review on the removal of hydrogen sulfide from biogas by adsorption using sorbents derived from waste. Rev. Chem. Eng. 2021, 37, 407–431. [Google Scholar] [CrossRef]
- Georgiadis, A.; Charisiou, N.; Goula, M. Removal of hydrogen sulfide from various industrial gases: A review of the most promising adsorbing materials. Catalysts 2020, 10, 521. [Google Scholar] [CrossRef]
- Liu, D.; Li, B.; Wu, J.; Liu, Y. Sorbents for hydrogen sulfide capture from biogas at low temperature: A review. Environ. Chem. Lett. 2020, 18, 113–128. [Google Scholar] [CrossRef]
- Speight, J. Natural Gas. A Basic Handbook, 2nd ed.; Gulf Professional Publishing: Cambridge, MA, USA, 2019; pp. 277–324. [Google Scholar] [CrossRef]
- Gao, S.; Brown, B.; Young, D.; Singer, M. Formation of iron oxide and iron sulfide at high temperature and their effects on corrosion. Corros. Sci. 2018, 135, 167–176. [Google Scholar] [CrossRef]
- Feng, Y.; Wen, J.; Hu, Y.; Wu, B.; Wu, M.; Mi, J. Evaluation of the cycling performance of a sorbent for H2S removal and simulation of desulfurization-regeneration processes. Chem. Eng. J. 2017, 326, 1255–1265. [Google Scholar] [CrossRef]
- Ning, J.; Zheng, Y.; Brown, B.; Young, D.; Nešić, S. The role of iron sulfide polymorphism in localized H2S corrosion of mild steel. Corrosion 2017, 73, 155–168. [Google Scholar] [CrossRef]
- Zhang, X.; Tang, Y.; Qu, S.; Da, J.; Hao, Z. H2S-selective catalytic oxidation: Catalysts and processes. ACS Catal. 2015, 5, 1053–1067. [Google Scholar] [CrossRef]
- Meyer, F.; Riggs, O.; McGlasson, R.; Sudbury, J. Corrosion products of mild steel in hydrogen sulfide environments. Corrosion 1958, 14, 69–75. [Google Scholar] [CrossRef]
- Watanabe, S. Chemistry of H2S over the surface of common solid sorbents in industrial natural gas desulfurization. Catal. Today 2021, 371, 204–220. [Google Scholar] [CrossRef]
- Raabe, T.; Mehne, M.; Rasser, H.; Krause, H.; Hureti, S. Study on iron-based adsorbents for alternating removal of H2S and O2 from natural gas and biogas. Chem. Eng. J. 2019, 371, 738–749. [Google Scholar] [CrossRef]
- Skerman, A.; Heubeck, S.; Batstone, D.; Tait, S. Low-cost filter media for removal of hydrogen sulphide from piggery biogas. Process Saf. Environ. Prot. 2017, 105, 117–126. [Google Scholar] [CrossRef] [Green Version]
- Ishida, M.; Wen, C. Comparison of zone-reaction model and unreacted-core shrinking model in solid-gas-reactions—I Isothermal analysis. Chem. Eng. Sci. 1971, 26, 103–1041. [Google Scholar] [CrossRef]
- Lim, S.; Jenkins, A.; Barbuto, K.; Crawshaw, M.; Brundick, W.; Juncker, M. Liquid Scavenger vs. Fixed Bed H2S Adsorbent. Working in Harmony or against Each Other for H2S Removal. In Proceedings of the CORROSION 2021, Virtual, 19-30 April 2021; Available online: https://onepetro.org/NACECORR/proceedings-abstract/CORR21/8-CORR21/D081S030R010/464031 (accessed on 1 July 2021).
- Todd, R.; Webley, P. Pressure drop in a packed bed under nonadsorbing and adsorbing conditions. Ind. Eng. Chem. Res. 2005, 44, 7234–7241. [Google Scholar] [CrossRef]
- Mao, D.; Karanikas, J.; Fair, P.; Prodan, I.; George, W. A different perspective on the Forchheimer and Ergun equations. SPE J. 2016, 21, 1501–1507. [Google Scholar] [CrossRef]
- Mayerhofer, M.; Govaerts, J.; Parmentier, N.; Jeanmart, H.; Helsen, L. Experimental investigation of pressure drop in packed beds of irregular shaped wood particles. Powder Technol. 2011, 205, 30–35. [Google Scholar] [CrossRef]
- Ozahi, E.; Gundogdu, M.; Carpinlioglu, M. A modification on Ergun’s correlation for use in cylindrical packed beds with non-spherical particles. Adv. Powder Technol. 2008, 19, 369–381. [Google Scholar] [CrossRef]
- Peng, D.; Robinson, D. A new two-constant equation of state. Ind. Eng. Chem. Fundam. 1976, 15, 59–64. [Google Scholar] [CrossRef]
- Jarrahian, A.; Heidaryan, E. A simple correlation to estimate natural gas viscosity. J. Nat. Gas Sci. Eng. 2014, 20, 50–57. [Google Scholar] [CrossRef]
- Huertas, J.; Quipuzco, L.; Hassanein, A.; Lansing, S. Comparing hydrogen sulfide removal eficiency in a field-scale digester using microaeration and iron filters. Energies 2020, 13, 4793. [Google Scholar] [CrossRef]
- Huang, G.; He, E.; Wang, Z.; Fan, H.; Shangguan, J.; Croiset, E.; Chen, Z. Synthesis and characterization of γ-Fe2O3 for H2S removal at low temperature. Ind. Eng. Chem. Res. 2015, 54, 8469–8478. [Google Scholar] [CrossRef]
- Davydov, A.; Chuang, K.; Sanger, A. Mechanism of H2S oxidation by ferric oxide and hydroxide surfaces. J. Phys. Chem. B 1998, 102, 4745–4752. [Google Scholar] [CrossRef]
- Ramirez, M.; Mendez, M.; Viloria, A. Effects of the water content on the performance of H2S scavengers. In Proceedings of the CORROSION 2004, New Orleans, LA, USA, 22 March 2004; Available online: https://onepetro.org/NACECORR/proceedings-abstract/CORR04/All-CORR04/NACE-04479/115844 (accessed on 1 July 2021).
- Kelm, K.; Mader, W. Synthesis and structural analysis of ϵ-Fe2O3. Z. Anorg. Allg. Chem. 2005, 631, 2383–2389. [Google Scholar] [CrossRef]
- Yamaguchi, S.; Wada, H. Formation de Fe2S3 cubique. Bull. Mineral. 1973, 96, 213–214. [Google Scholar] [CrossRef]
- Sadegh-Vaziri, R.; Babler, M. Removal of hydrogen sulfide with metal oxides in packed bed reactors—a review from a modeling perspective with practical implications. Appl. Sci. 2019, 9, 5316. [Google Scholar] [CrossRef] [Green Version]
- Zhang, R.; Wang, B.; Wei, L. Sulfidation growth and characterization of nanocrystalline ZnS thin films. Vacuum 2008, 82, 1208–1211. [Google Scholar] [CrossRef]
- Fogler, S. Elements of Chemical Reaction Engineering, 3rd ed.; Prentice-Hall India: New Delhi, India, 2004; ISBN 81-203-2234-7. [Google Scholar]
- Hussain, K.; Ismail, F.; Senu, N. Solving directly special fourth-order ordinary differential equations using Runge–Kutta type method. J. Comput. Appl. Math. 2016, 306, 179–199. [Google Scholar] [CrossRef]
- de Angelis, A. Natural gas removal of hydrogen sulphide and mercaptans. Appl. Catal. B: Environ. 2012, 113–114, 37–42. [Google Scholar] [CrossRef]
- Di Felice, R.; Pagliai, P. Prediction of the early breakthrough of a diluted H2S and dry gas mixture when treated by Sulfatreat commercial sorbent. Biomass Bioenergy 2015, 74, 244–252. [Google Scholar] [CrossRef]
- Papadias, D.; Ahmed, S.; Kumar, R. Fuel quality issues with biogas energy—An economic analysis for a stationary fuel cell system. Energy 2012, 44, 257–277. [Google Scholar] [CrossRef]
- Cherosky, P.; Li, Y. Hydrogen sulfide removal from biogas by bio-based iron sponge. Biosyst. Eng. 2013, 114, 55–59. [Google Scholar] [CrossRef]
- Green, D.; Perry, R. Perry’s Chemical Engineers’ Handbook, 8th ed.; McGraw-Hill Professionals: New York, NY, USA, 2008; ISBN 978-0-0714-294-9. [Google Scholar]
- Koekemoer, A.; Luckos, A. Effect of material type and particle size distribution on pressure drop in packed beds of large particles: Extending the Ergun equation. Fuel 2015, 158, 232–238. [Google Scholar] [CrossRef]
- Aguilera, P.; Gutiérrez, F. Prediction of fixed-bed breakthrough curves for H2S adsorption from biogas: Importance of axial dispersion for design. Chem. Eng. J. 2016, 289, 93–98. [Google Scholar] [CrossRef]
- Couper, J.; Penney, W.; Fair, J.; Walas, S. Chemical Process Equipment. Selection and Design, 3rd ed.; Butterworth-Heinemann: Waltham, MA, USA, 2012. [Google Scholar] [CrossRef]
- Martín, M. Industrial Chemical Process Analysis and Design, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2016. [Google Scholar] [CrossRef]
- Wang, H.; Wang, D.; Chuang, K. A sulfur removal and disposal process through H2S adsorption and regeneration: Breakthrough behavior investigation. Process Saf. Environ. Prot. 2011, 89, 53–60. [Google Scholar] [CrossRef]
- Zicari, S. Removal of Hydrogen Sulfide from Biogas Using Cow-Manure Compost. Master’s Thesis, Master of Science Program. Cornell University, Ithaca, NY, USA, 2003. Available online: https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.470.2484&rep=rep1&type=pdf (accessed on 1 July 2021).
- Anerousis, J.; Whitman, S. An updated examination of gas sweetening by the iron sponge process. In Proceedings of the 59th Annual Technical Conference and Exhibition, Houston, TX, USA, 16–19 September 1984. [Google Scholar] [CrossRef]







| Properties | Base Case | Case studies | References | ||
|---|---|---|---|---|---|
| Minimum | Maximum | ||||
| Natural gas stream | C1 content (mole %) | 52.56 | 39.59 | 64.21 | [1] |
| H2S content (mole ppm) | 300 | 150 | 450 | [7] | |
| Pressure (kPa) | 3447.38 | 344.74 | 5171.07 | [4] | |
| Temperature (K) | 310.93 | 288.15 | 323.15 | [11] | |
| Flowrate (*) (MMSCFD) | 25 | 2.5 | 100 | [17,38] | |
| H2S specification (mole ppm) | 4 | 2 | 10 | [7] | |
| Solid sorbent | Adsorption capacity (Kg H2S/Kg Solid) | 0.24 | 0.05 | 0.80 | [39,40] |
| Particle diameter (cm) | 0.33 | 0.1 | 1.5 | [41,42] | |
| Sphericity | 0.7 | 0.5 | 1 | [43] | |
| Bed void fraction | 0.3 | 0.2 | 0.7 | [43,44] | |
| Bed density (Kg/m3) | 1491.16 | 800.93 | 1601.85 | [39,40] | |
| Fixed-bed vessel | Diameter (m) | 3.05 | 0.31 | 3.35 | [45,46] |
| Length/diameter ratio | 3 | 2 | 4 | [36,45] | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carrasco, B.; Ávila, E.; Viloria, A.; Ricaurte, M. Shrinking-Core Model Integrating to the Fluid-Dynamic Analysis of Fixed-Bed Adsorption Towers for H2S Removal from Natural Gas. Energies 2021, 14, 5576. https://doi.org/10.3390/en14175576
Carrasco B, Ávila E, Viloria A, Ricaurte M. Shrinking-Core Model Integrating to the Fluid-Dynamic Analysis of Fixed-Bed Adsorption Towers for H2S Removal from Natural Gas. Energies. 2021; 14(17):5576. https://doi.org/10.3390/en14175576
Chicago/Turabian StyleCarrasco, Bryan, Edward Ávila, Alfredo Viloria, and Marvin Ricaurte. 2021. "Shrinking-Core Model Integrating to the Fluid-Dynamic Analysis of Fixed-Bed Adsorption Towers for H2S Removal from Natural Gas" Energies 14, no. 17: 5576. https://doi.org/10.3390/en14175576
APA StyleCarrasco, B., Ávila, E., Viloria, A., & Ricaurte, M. (2021). Shrinking-Core Model Integrating to the Fluid-Dynamic Analysis of Fixed-Bed Adsorption Towers for H2S Removal from Natural Gas. Energies, 14(17), 5576. https://doi.org/10.3390/en14175576