Effect of Connection Resistance between Cyclones and Backpass on Furnace Solids Suspension Density Profile and Circulation Rates in CFB

Abstract

The connection section between cyclones and backpass is an important configuration in multi-cyclone circulating fluidized bed boilers (CFB). In this work, the resistance coefficient of different connection modes, and connection resistance distribution from each cyclone outlet to backpass (connection branch) in one mode are defined and calculated, in order to investigate their effects on furnace solids suspension density distribution and circulation rates. Three connection modes with different overall resistance coefficients were tested experimentally and analyzed by a 1.5-dimensional model in a four-cyclone scaling CFB apparatus. Both experimental and theoretical results show that, with larger overall resistance of a connection, there are more solids suspended in the furnace bottom and fewer in the top section. The investigation of the C-type connection has revealed that when the branch resistance of the connection decreases from branch No. 1–4, the solids suspension density and circulation rate from corresponding solids recycle loops (No. 1–4) increase. Moreover, the non-uniformity of connection branch resistance distribution will lead to uneven lateral solids suspension density distribution and circulation rates allocation. This effect is enhanced by growing superficial velocity.

1. Introduction

Circulating fluidized bed boilers have been widely utilized in the industry due to their high combustion efficiency, low emission, and fuel adaptability. As the boiler’s capacity increased, the furnace size becomes larger, and more cyclones with solid recycle systems are applied. However, the distributions of solids suspension density on the cross-section in the furnace and solids circulation rates under each cyclone become more non-uniform. This will lead to an uneven temperature profile in a CFB furnace and then cause operation problems.

Previous studies have been conducted towards gas-solid hydrodynamics uniformity in a CFB with multiple cyclones. Results show operating conditions [1,2,3,4,5,6,7] and geometric factors [6,7,8,9,10,11] have influences on furnace solids suspension density and circulation rates distribution among cyclones. However, it was reported that the connection between cyclones and backpass might also have an effect. As some close research, Zhou et al. [1] indicated the non-uniform distributions of cyclone pressure drop in a symmetric six-cyclone CFB cold test rig, that the pressure drops of three cyclones implemented at the one side are 30–50 Pa greater than the cyclones in the other side. They attributed this effect to unequal length of connection ducts from cyclones to backpass at each side, leading to different resistance of connection ducts from both sides. Similarly, Song et al. [12] also discovered the better solid flow uniformity of three circulation loops on one side than another three loops in a six-cyclone 600 MW CFB boiler. And they further put forward that the different connection resistance at each side might result in this. In addition, Mo et al. [13] reported the higher ash temperature and lower circulation rate in the solid recycle loops, if they were located further to the backpass in a multi-cyclone CFB boiler. With pressure equilibrium analysis, they proposed the reason is those solid recycle loops have larger resistance from cyclone outlet to backpass compare to other loops.

As the studies indicated above, the connection between cyclones and backpass has a potential impact on solids suspension profile in furnace and circulation rates distribution in a CFB. The connection resistance and resistance distribution from each cyclone outlet to backpass (connection branch) are reported essential to this. However, detailed studies on connection resistance and resistance distribution among connection branches are lacking. And their effect on furnace solids suspension density and circulation rates distribution in a CFB also remain unknown.

For those reasons, this article focuses on the connection between cyclones and backpass, to investigate the effect of connection resistance on furnace solids suspension density and solids circulation rates in a CFB.

Firstly, a four-cyclone scaling CFB model with measuring techniques is introduced in this article. Then, the definition and calculation of branch resistance in a connection, and overall resistance of A, B, and C-type connection modes are presented. To step further, a 1.5-dimentional theoretical model based on mass and pressure equilibrium is established to analyze the relationship among connection resistance, solids suspension density distribution, and solids circulation rates. After experimental system description and theoretical analysis, the results of solids suspension density and solids circulation rates with different connection modes of overall resistance are presented. Besides, this work also focuses on a particular connection mode (C-type mode) to explore the impact of resistance distribution among connection branches, so that the relationship among connection branch resistance distribution, furnace solids suspension density, and circulation rates allocation among four solids recycle loops will be discovered. Eventually, the influence of superficial velocity on furnace suspension density profile and solids circulation rates under different connections is investigated, with Fn conditions of 85.2, 91.4, 96.3, and 102.5.

2. Experimental Setup

2.1. Basic Information of the CFB Test Rig

The experiment was conducted on a CFB cold test rig (shown in Figure 1a). It consists of a furnace, four cyclones, solids recycle systems and a connection to the backpass. The bed solids were fluidized by primary and secondary air in the furnace and then entered the cyclones. The air exited from the cyclone outlets passes through the connection section to the backpass, then finally escapes to the atmosphere. Those solids collected by the cyclones return to the furnace via the solids recycle system.

The geometric, operating, and bed material parameters are determined by a simplified fluid dynamic scaling rule [14] based on a 660 MW supercritical CFB boiler. In the simplified Glicksman scaling law, a set of dimensionless groups are derived from governing equations of motion and mass. The dimensionless parameters are identified as:

$$\frac{u_g^2}{\mathrm{g}L},\frac{u_g}{u_{mf}},\frac{G_{sf}}{{\rho }_s{u}_g},\frac{D}{L},\Phi ,PSD$$

(1)

whereas u_g and u_mf are superficial velocity and minimum fluidized velocity respectively; L and D are the length and width of the furnace; G_sf is solids flux at furnace and ${\rho }_s$ is solid density; The Φ is the sphericity of the particle; PSD is particle size distribution.

It needs to be noticed that only when particle Reynolds number Re_p in the model is equal to or less than 4, the simplified scaling law can be used [15].

Based on Glicksman scaling law, the geometric structure of the testing model is scaled down by 1:40 from the original CFB boiler. Besides, the operating parameters of the cold apparatus are designed and calculated.

Table 1. Scaling parameters of original boiler and cold model.

	Items	Symbols	Units	Values in Original Boiler	Values in Test Model
Geometric parameters	Height of furnace	H	m	55.8	1.39
	Length of furnace	L	m	39.95	0.99
	Width of furnace	D	m	12.67	0.32
	Diameter of cyclone	dc	m	11.20	0.28
	Diamter of standpipe	ds	m	2.12	0.053
	cross-section of the non-mechanical valve	Adis	m2	4.84	0.0030
Operating conditions	Temperature	T	°C	880	25
	superficial velocity	ug	m/s	4.37–5.26	0.69–0.83
	Air velocity in supply chamber	uvs	m/s	−	0.063
	Air velocity in recycle chamber	uvr	m/s	−	0.19–0.38
	Kinematic viscosity	ν	Pa·s	1.51 × 10−4	1.55 × 10−5
	Air density	ρf	kg/m3	0.301	1.185
	Solids flux at furnace	Gsf	kg/m2s	16.56	3.14
	Solids flux at a standpipe	Gsp	kg/m2s	678.96	128.74
Bed material properties	Solid diameter	dp	um	400	94
	Sphericity	Φ	\	0.8	0.8
	Minimum fluidized velocity	umf	m/s	0.052	0.0081
	Terminal velocity	ut	m/s	2.91	0.66
	Particle Reynolds number	Rep	\	11.13	4.02
	Solid density	ρs	kg/m3	2000	2330
Dimensionless numbers	ug2/gL		\	0.069	0.070
	D/L		\	0.317	0.320
	ug/umf		\	102.08	102.11
	Gsf/ρsug		\	1.57 × 10−3	1.57 × 10−3

gives the basic geometric parameters, operating conditions, bed material properties, and dimensionless numbers of both the original boiler and cold model. As shown in the table, all the dimensionless numbers between the cold model and the original boiler are nearly equaled. In addition, the particle Reynolds number in the cold model is close to 4, which corresponds to the viscous limit condition for the simplified Glicksman scaling law.

2.2. Measurement Techniques

The solids suspension density in the furnace was determined by the pressure drop. As shown in Figure 1b, there are three vertical rows of pressure measuring points along the bed length and 5 points in each row along with the bed height. The pressure taps were used to measure the furnace pressure profile. And solids suspension density ρ_sus is calculated as

$${\rho }_{sus}=\frac{\Delta P}{\mathrm{g}\Delta H}$$

(2)

where ΔP is the pressure drop between two axial measuring positions with a distance of ΔH. And g is gravitational acceleration with 9.81 m/s².

The solids circulation rate was measured at standpipe. Two methods were used to determine the solids circulation rate. The first one is measuring the height of the accumulating solid by cutting off the solids returning flow in the return leg within a specific time. The calculating solids circulation rate at standpipe “i” (i = 1–4) is expressed as,

$$G_{sp,i}=\frac{{\rho }_s\left(1-{\epsilon }_{mf}\right)h_s}{t_s}$$

(3)

where h_s are the solids accumulating height within the specific time t_s.

Another methodology is particle tracking using a high-speed camera to trace the moving particles in the standpipe. The camera for tracking particles is HG-100K high-speed digital camera (REDLAKE company, New Hampshire, USA), with a resolution of 1154 × 1128 and a frame rate (fps) of 125. The colored particles with similar density and diameter to bed material were used as tracer particles. For this method, the solids circulation rate at the standpipe “i” can be calculated as

$$G_{sp,i}={\rho }_s\frac{s}{t}$$

(4)

where s is the falling distance of tracer particle within specific time t. Figure 2 shows several successive frames of the capturing procedure. To ensure the accuracy of measuring, two or more colored particles with a similar relative location in each frame were treated as valid particles. And up to 1000 frames were used in total to measure and calculate G_sp,i at each operating condition.

3. Three Connection Modes and Calculation of Connection Resistance

Three connection modes were tested in the cold apparatus as given in Figure 3. The overall resistance coefficients of each connection mode (ξ_av) were calculated based on the Handbook of Hydraulic Resistance [16]. They were determined by averaging the resistance coefficient of the four connection branches (ξ_b,i).

3.1. Resistance Coefficient of Each Connection Branch of a Connection Mode

The CFB system has four parallel cyclones, and the gas escaped from each cyclone outlet enters the connection section. Therefore, the connection section consists of four branches, starting from each cyclone outlet to the end of the connection, as illustrated in Figure 4. The resistance coefficient of a connection branch (ξ_b,i, i = 1–4) is calculated by summing the friction resistance coefficient along the path (ξ_fr,i) and local resistance coefficients (ξ_l,i) such as a sudden variation of cross-section area. The expression is given by,

$${\xi }_{b,i}={\xi }_{fr,i}+{\xi }_{l,i} \left(\mathrm{i}=1–4\right)$$

(5)

For a connection branch i, the friction resistance coefficient can be expressed as,

$${\xi }_{fr,i}=\mathsf{\lambda }\sum \frac{l}{D_h}$$

(6)

where λ refers to friction coefficient constant, l and D_h are the lengths and hydraulic diameter of the branch path, while the sections along the path might have different D_h.

ξ_l,i is the local resistance coefficient, which is mainly decided by geometric parameters. According to Figure 4, taking branch 1 of the C-type connection as an example, the local resistance from the beginning to the end of this branch consists of an elbow, sudden expansion, tees junction, smooth variation, and horizontal band.

The frictional and local resistance coefficients of, A, B, and C-type modes are listed in

Table 2. Resistance coefficient calculation.

Connection Mode	Connection Branch (i)	ξfr,i	ξl,i	Detailed of Local Resistance	ξb,i	ξav
A-type	1 and 4	0.13	1.51	Elbow with right angle, conjunction wye with angle, sudden expansion*2	1.64	1.58
	2 and 3	0.09	1.43	Elbow with right angle, conjunction wye with angle, sudden expansion*2	1.52
B-type	1 and 4	0.12	1.60	Elbow with right angle, conjunction wye with angle, sudden expansion*2, smooth expansion	1.82	1.70
	2 and 3	0.09	1.49	Elbow with right angle, conjunction wye with angle, sudden expansion*2, smooth expansion	1.58
C-type	1	0.16	3.10	elbow, sudden expansion, tee (after junction) *3, smooth expansion, horizontal elbow with sharp corner	3.26	2.89
	2	0.12	2.98	Tee before junction, tee after junction*2, smooth expansion, horizontal elbow with sharp corner	3.10
	3	0.08	2.66	Tee before junction, tee after junction, smooth expansion, horizontal elbow with sharp corner	2.74
	4	0.06	1.96	tees before junction and horizontal elbow with sharp corner	2.02

. It is noted that the branches 1–4 of, A, B, and C-type are numbered based on cyclones’ positions from left to right from the view the of furnace front wall, as hinted in Figure 4. Therefore, concerning symmetric structure of A and B-type connection modes, the connection resistance coefficient of branches 1 and 4, 2 and 3 of both A and B-type connections are equaled, respectively.

3.2. Overall Resistance Coefficient of a Connection Mode

For each type of connection mode, the connection section is divided into four parallel branches. Therefore, the overall resistance coefficient of a connection mode can be determined by averaging four branch resistance coefficients,

$${\xi }_{av}=\frac{1}{4}{\displaystyle \sum }_{i=1}^4{\xi }_{b,i}$$

(7)

As given in Table 2, the overall resistance coefficient of A, B, and C type connection modes are 1.58, 1.70, and 2.89 respectively. Other details about connection branch resistances are also given in Table 2.

4. Theoretical Analysis

In order to analyze the effect of the connection resistance on solids suspension density in furnace and solids circulation rates distribution theoretically, a 1.5-dimension model based on mass and pressure balance of the CFB system is deduced.

4.1. Solids Recycle Loops and Gas-Flowing Branches

Solids recycle loop and gas-flowing branch in multi-cyclone CFB are defined in Figure 5. The furnace’s cross-section is divided into four sections along the bed width, corresponding to four solids recycle systems. A divided furnace section, cyclone, and solids recycle system constitute one of the solids recycle loops (A-B-C-D-A). Similarly, the divided furnace section, cyclone, and connection branch (A-B-E-F) compose a gas-flowing branch, as shown in Figure 5. In the theoretical model, it is assumed gas-solid lateral interactions in the furnace upper section can be ignored, and solids lateral dispersion in the bottom dense section is counted [17].

For the reason of much narrower cross-section in a divided furnace, some researches regarding CFB riser are considered reasonable here. And each gas-flowing branch or solids recycle loop is denoted by subscript “i” in the following theoretical analysis.

4.2. Pressure Drops from Furnace to Each Connection Branch

For branch A-B-E-F, the pressure drop relationship is expressed by the following equation,

$$\Delta P_{AF,i}=\Delta P_{AB,i}+\Delta P_{BE,i}+\Delta P_{EF,i}$$

(8)

where ΔP_AB,i, ΔP_BE,i and ΔP_EF,i are the pressure drops across the furnace, cyclone, and the connection branch respectively. Since the primary air is evenly distributed above the distributor, ΔP_AF,i is identical for all four gas-flowing branches.

ΔP_AB,i can be obtained as following [18],

$$\Delta P_{AB,i}={\rho }_{av,i}g\left(H-h_0\right)+{\rho }_{a,i}g{h}_0$$

(9)

where ${\rho }_{a,i}$ refers to solids suspension density in the bottom dense region with a height of h₀. ${\rho }_{av,i}$ refers to axial average solids suspension density above h₀. The dense region height h₀ was taken approximately as 0.26 m.

The pressure drop across the cyclone is estimated by Equation (10) [19]:

$$\Delta P_{BE,i}=\frac{1}{2}\left(\frac{16A_c}{D_e^2}\right){\rho }_g{u}_{gc,i}^2$$

(10)

where A_c, D_e and u_gc,i represent the cross-section area, hydraulic diameter, and gas velocity at the cyclone entrance, respectively.

Pressure drop across a connection branch ΔP_EF,i can be calculated by,

$$\Delta P_{EF,i}=\frac{1}{2}{\xi }_{b,i}{\rho }_g{u}_{go,i}^2$$

(11)

where $u_{go,i}$ is the equivalent gas velocity in a specific connection branch, ${\xi }_{b,i}$ represents the resistance coefficient of a connection branch calculated by Equation (5) in the previous section.

4.3. Pressure Drops in a Solids Recycle Loop

The sum of pressure drops of solids recycles loop is zero when the system operates steadily. It can be written as,

$$\Delta P_{AB,i}+\Delta P_{BC,i}+\Delta P_{CD,i}+\Delta P_{DA,i}=0$$

(12)

where $\Delta P_{AB,i}$, $\Delta P_{BC,i}$, $\Delta P_{CD,i}$ and $\Delta P_{DA,i}$ are the pressure drops across furnace, cyclone, standpipe, and loop-seal, respectively.

Here $\Delta P_{AB,i}$ and $\Delta P_{BC,i}$ are calculated according to Equations (9) and (10), respectively [20,21]. The pressure drop $\Delta P_{CD,i}$ in the standpipe of is calculated neglecting solids frictional or acceleration losses in standpipe [21]. It can be given,

$$\Delta P_{CD,i}={\rho }_s\left(1-{\epsilon }_{mf}\right)g{L}_i$$

(13)

here L_i is solids stacking height in a standpipe.

The pressure drop across the non-mechanical valve can be written as [22],

$$\Delta P_{DA,i}=\frac{1}{2{\rho }_s\left(1-{\epsilon }_{mf}\right)}{\left(\frac{G_{sp,i}{A}_{sp}}{C_d{A}_{dis}\varnothing }\right)}^2$$

(14)

where A_dis is the vertical cross-section of the non-mechanical valve, ∅ is sphericity of the particle and C_d is a discharge coefficient about 0.7–0.8 for all kinds of systems and a mid-value of 0.75 was adopted.

4.4. Mass Balance of the Loop in the Whole System

Neglected the solids escaping from the cyclones, the solids mass is balanced in the CFB systems as following,

$$M=M_{sp}+M_f+M_{cyc}$$

(15)

where M is the total inventory in the system, which is 25 kg in this study. M_sp, M_f and M_cyc are the mass of solids in standpipes, furnace, and cyclones respectively. They can be written as following equations,

$$M_{sp}={\rho }_s\left(1-{\epsilon }_{mf}\right)A_{sp}{{\displaystyle \sum }}_{i=1}^4{L}_i$$

(16)

$$\begin{gathered} M_f=\left({{\displaystyle \sum }}_{i=1}^4{\rho }_{a,i}\right)A_{fb}{h}_0+\left({{\displaystyle \sum }}_{i=1}^4{\rho }_{av,i}\right)A_{fd}\left(H-h_0\right) \\ ={\overline{\rho }}_a{A}_{fb}{h}_0+\left({{\displaystyle \sum }}_{i=1}^4{\rho }_{av,i}\right)A_{fd}\left(H-h_0\right) \end{gathered}$$

(17)

$$M_{cyc}=k{{\displaystyle \sum }}_{i=1}^4{\rho }_{e,i}$$

(18)

where $A_{fb}$, $A_{fd}$ and $A_{sp}$ are the cross-section area of furnace bottom, furnace above dense phase and standpipe, respectively; $M_{cyc}$ is calculated on the assumption that the solids concentration in the cyclone is the linear function to that of the dilute phase at the furnace exit [13]; ${\rho }_{e,i}$ is the solids suspension density at each furnace exit; ${\overline{\rho }}_a$ is the average solids suspension density at furnace bottom zone.

4.5. Solids Suspension Density Distribution in the Furnace

For each solids recycle loop, the axial solids suspension density above the dense region can be calculated by Kunii-Levenspiel Equation [23],

$$\frac{{\rho }_{d,i}-{\rho }_i}{{\rho }_{d,i}-{\rho }_{a,i}}=Exp\left[-a_{\epsilon ,i}\left(h-h_0\right)\right]$$

(19)

where $a_{\epsilon ,i}$ is an axial attenuate coefficient, with the relationship of $a_{\epsilon ,i}·u_{g,i}=C$, here C increase from 4–12 with particle diameter from 88–369 μm. Considering 94 μm of particle diameter in this work, the C value of 4 is adopted.

Besides, ${\rho }_{d,i}$ stands for saturated solids carrying capacity of gas, equivalent to solids suspension density at choking [24,25]. In this work, ${\rho }_{d,i}$ is calculated based on Yang’s Equation [25],

$$\frac{2g{D}_i\left({\epsilon }_{d,i}^{-4.7}-1\right)}{{\left(u_{g,i}-u_t\right)}^2}=6.81\times {10}^5\frac{{\rho }_g}{{\rho }_s}$$

(20)

where D_i is the hydraulic diameter of the furnace section of a branch. ${\epsilon }_{d,i}$ is choking voidage, also equivalent to the volume fraction of gas when saturated carrying occurs.

Then ${\rho }_{d,i}$ can be calculated as Equation (21) [23],

$${\rho }_{d,i}={\rho }_g{\epsilon }_{d,i}+{\rho }_s\left(1-{\epsilon }_{d,i}\right)$$

(21)

For the reason that the solids concentration in the bottom zone always has a lower value in the center of the furnace and increases towards the wall, ${\rho }_{a,i}$ can be determined by the modified Patience-Chaouki Equation [26],

$$\frac{{\overline{\epsilon }}_a^{0.6}-{\epsilon }_{a,i}}{{\overline{\epsilon }}_a^{0.6}-{\overline{\epsilon }}_a}=3{\left(\frac{r}{R}\right)}^4$$

(22)

where r is the horizontal distance to the centerline of the furnace bed width and R equals half bed width in a rectangular cross-section furnace. ${\overline{\epsilon }}_a$ is the average voidage at the furnace bottom. ${\overline{\rho }}_g$ as well as ${\rho }_{a,i}$ can be calculated similarly to Equation (21) accordingly.

Eventually, solids suspension density at furnace exit ${\rho }_{e,i}$ can be calculated by equation,

$${\rho }_{e,i}={\rho }_{d,i}-\left({\rho }_{d,i}-{\rho }_{a,i}\right)Exp\left[-a_{\epsilon ,i}\left(H-h_0\right)\right]$$

(23)

4.6. Solids Circulation Rates

The solids circulation rate at the standpipe in each recycle loop can be calculated by the following equation [27],

$$G_{sp,i}={\rho }_{e,i}\left(u_{g,i}-u_t\right)\frac{A_f}{A_{sp}}$$

(24)

where u_t is solid terminal velocity. The calculation of u_t is provided in Appendix A.

Furthermore, the average solids circulation rate among four loops at standpipe G_sp can be calculated,

$$G_{sp}=\frac{1}{4}{{\displaystyle \sum }}_{i=1}^4{G}_{sp,i}$$

(25)

4.7. Solution Procedure

With the equations listed above, the furnace solids suspension density distribution and solids circulation rate at standpipe can be determined for each solids recycle loop. They are related to the resistance coefficient of each branch in the connection between cyclones and backpass. Figure 6 gives the solution procedure of the theoretical model.

The calculated value of pressure drops across the furnace, cyclones, and the connection are provided in Appendix B. The experimental data of pressure drops across the furnace and cyclones are also given there.

5. Results and Discussion

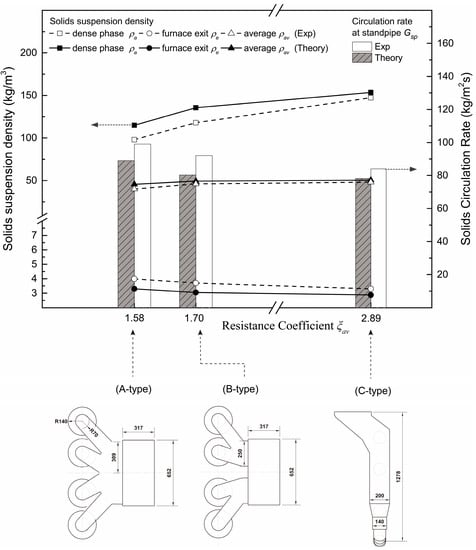
5.1. Effect of Overall Resistance Coefficient on Suspension Density Distribution and G_sp

Figure 7 shows solids suspension density distribution along with the furnace height with different overall resistance coefficient ξ_av, from connection modes including A-type, B-type, and C-type. The theoretical results match well with the experimental data.

As mentioned in Section 3.2, the A-type connection mode has the smallest value of overall connection resistance coefficient ξ_av. Figure 7 shows the largest suspension density in the furnace above the dense section compared to the other two connections. Besides, the smoothest slope of the suspension density curve along the height of the A-type mode can also be discovered. In contrast, there are fewer solids suspended in the furnace of the B and C-type connection modes, and their suspension density curves along bed height are steeper, reflecting more uneven axial suspension density distribution. This indicates the hydraulic resistance of the connection section affects the solids suspension density distribution in the furnace. Higher pressure resistance of the connection may result in a hindrance curtain at the exit of the furnace so as to prevent the gas-solid up-flowing from the furnace bottom to the top. As a result, the solids suspension density is distributed more non-uniformly in the furnace as ξ_av increases.

Figure 8 gives the results of the solids suspension density at specific heights and the average solids circulation rate among standpipes (G_sp) with respect to the overall resistance coefficient ξ_av. As illustrated in the figure, the solids suspension density in dense phase (${\rho }_a$) of C-type mode is around 30 kg/m³ larger than that of A-type mode, while the concentration in furnace exit (${\rho }_e$) is 1.8 kg/m³ less. In terms of average solids circulation rate among four standpipes (G_sp), the A-type mode has the largest G_sp value of near 100 kg/m²s which is around 20 kg/m²s larger than that of C-type mode.

Sum up with both Figure 7 and Figure 8, ${\rho }_a$ has the same trend as resistance coefficient ξ_av variation, while ${\rho }_e$ and G_sp changes with ξ_av reversely. Meanwhile, the average solids suspension densities (${\rho }_{av}$) do not change much for different ξ_av.

From those results, it can be deduced that there are more solids transferred from the bottom to the upper furnace when the solids circulation rate increases and the solids circulation is intensified by smaller resistance of a connection. The high circulation rate exerts an effect on larger solids suspension density in the upper dilute zone. Therefore, small ξ_av in a connection mode would cause less hindrance for solids circulation and lifting, resulting in better uniformity of axial gas-solid distribution profile.

5.2. Effect of Connection Branch Resistance Distribution on Suspension Density and G_sp,i

To study the effect of the resistance distribution among connection branches on solids suspension density and the solids circulating rates (G_sp,i) allocation further, more works were done on C-type connection mode.

The structure of the C-type connection was given in both Figure 4 and Figure 9, there are four exit branch ducts extended from four cyclone outlets. Those ducts compile at different positions successively, forming four connection branches (No. 1–4) for gas flowing from each cyclone outlet to the backpass. As depicted from Figure 9, the resistance coefficients of the connection branches (ξ_b,i) decrease from branch 1 to 4 as 3.3–2.0, and the value of ξ_b,i is smaller if the corresponding branch is closer to backpass.

Figure 10 gives the solids suspension density distribution on the view of the furnace front wall obtained from the experiments and theoretical calculation. The experimental contour presents the solids suspension density in the furnace from three rows of measuring points (shown in Figure 1b). And the theoretical contour diagram shows the solids suspension density with dimensionless length from 0.2 to 0.8 which corresponding to the theoretical gas-flowing branch 1 to 4 in the furnace, as shown in Figure 5. It can be seen that solids suspension density in the dilute section increases from left to right, with around 3 kg/m³ variance between branches 1 and 4. And lateral density distribution in the furnace below the transition section (H/h = 0.3–0.5) remains relatively uniform for both experimental and theoretical contours.

Figure 11 shows the relationship of standpipe circulation G_sp,i distribution among each standpipe, corresponding to each connection branch. Both experimental and theoretical results presented higher G_sp,i at lower resistance ξ_b,i of a connection branch. To be specific, the circulation rate in branch 4 is the largest and 45 kg/m²s greater than that in branch 1. The relationship between G_sp,i, and ξ_b,i have a similar trend as solids suspension density in the dilute section in Figure 10.

Combined with Figure 10 and Figure 11, it can be summarized that higher ξ_b,i of a connection branch may also hinder solids circulation in the corresponding solids recycle loop and consequently reduce furnace solids suspension density in this gas-flowing branch. And the axial solids suspension density distributed more non-uniform with higher ξ_b,i of a connection branch.

5.3. Effect of Superficial Velocity on Suspension Density and Circulation Rate

The superficial velocity has a strong impact on furnace solids suspension density distribution, solids circulation rates, and their uniformity. In this section, four different velocity conditions are tested with Fn number of 85.2, 91.4, 96.3, 102.5, and corresponding velocities of 0.68, 0.73, 0.78, 0.83 (m/s). The lower limit of the velocity conditions is considering terminal velocity’s value of 0.66 m/s that superficial velocity should be larger than that. And the upper limit of 0.83 m/s corresponds to the superficial velocity of the original boiler of 5.26 m/s at 100% Boiler Maximum Continuous Rating (BMCR).

Figure 12 presents the effect of superficial velocity on a solids suspension density on the above furnace dense zone in three connection modes. A smoother curve and larger values of the solids suspension density are achieved when ξ_av of a connection mode decreases at all velocities. For different velocity conditions, the axial variance of the solids suspension becomes larger with growing superficial velocity, especially at the lower section.

Figure 13 gives the effect of superficial velocity on a solids suspension density from C-type connection mode. The No. 4 connection branch, with the smallest resistance coefficient ξ_b,i, has the largest solids suspension density in the furnace. The suspension density distribution curves show a similar trend with the results from different connection modes in Figure 12. That is, the effect of connection resistance on solids suspension distribution variation can be intensified by increasing superficial velocity. This intensification is most stimulated in the furnace lower section.

Figure 14 presents the effect of superficial velocity on solids circulation rates with different ξ_av. Both theoretical and experimental results show average circulation rate G_sp increases with the superficial velocity in all cases. A circulating system with smaller overall connection resistance ξ_av has a larger circulation rate. It can also be depicted from the figure that, for all connection modes, once increasing the superficial velocity, the value of G_sp and range of G_sp,i among standpipes are enlarged. This indicates higher non-uniformity of G_sp,i with increasing superficial velocity. And the velocity effect is most stimulated in C-type mode, probably because of its most uneven ξ_b,i distribution.

The effect of superficial velocity on G_sp,i in each solids recycle loop from the C-type connection mode is shown in Figure 15. Increasing superficial velocity intensifies solids circulation rate at all recycle loops. However, this enhancement effect varies with different recycle loops (standpipe No.). The recycle loop with larger corresponding ξ_b,i (e.g., No. “1”) has slighter changes in circulation rate with superficial velocity. On contrary, the recycle loop No. “4” has the smallest corresponding ξ_b,i, and its circulation rate increases most enormously with superficial velocity. The different responding effects for superficial velocity among each standpipe can also explain the phenomenon in Figure 14 that, the non-uniformity among G_sp,i is enlarged with growing superficial velocity.

Combined with Figure 12, Figure 13, Figure 14 and Figure 15, it is apparent that the non-uniformity of furnace solids suspension distribution and solids circulation rate caused by connection resistance is enhanced by superficial velocity. This can be further analyzed that, although ξ_av of connection or ξ_b,i among branches is constant, the connection pressure drop (ΔP_EF,i in Equation (8) and variation among ΔP_EF,i in different branches are increased by growing velocity. As a result, the furnace gas-solid distribution profile and circulation rates allocation become more uneven with increasing superficial velocity.

6. Conclusions

6.1. The Conclusions for the Investigation

The effect of connection resistance between cyclones and backpass on furnace solids suspension density distribution and solids circulation rates in a multi-cyclone CFB was investigated. The main conclusions are:

(1)

The solids suspension density in the furnace and solids circulation rate distributions are influenced by connection resistance. With smaller overall resistance coefficient ξ_av of a connection, the axial solids suspension density in the furnace distributes more uniform and solids circulation rate becomes larger;

(2)

For branch resistances ξ_b,i (i = 1–4) in a connection, smaller ξ_b,i leads to higher solids circulation rate in solids recycle loop. Regarding C-type connection mode, the ξ_b,i is decreasing from connection branch 1~4, resulting in solids suspension density and circulation rates increasing from corresponding recycle loop 1–4. Smaller ξ_b,i of a connection branch also leads to more evenly axial solids suspension density distribution of corresponding recycle loop;

(3)

The effect of connection resistance is enhanced by growing superficial velocity. The variance of lateral solids suspension distribution and solids circulation rates allocation becomes larger with higher superficial velocity. For a connection, non-uniformity of branch resistance ξ_b,i affects the uneven distribution of solids suspension density and G_sp,i allocation among recycling loops, this effect is strongly intensified by growing velocity.

6.2. Suggestions for the Connection Design of Large Scale CFB Boiler

The connection resistance and its distribution between cyclones and backpass should be paid more attention when designing an industry CFB boiler. Some suggestions are given as follows,

(1)

It is beneficial to design a simple connection structure with a short distance from cyclones to the backpass. A a small value of overall connection resistance coefficient ξ_av should be chosen, for it leads to less resistance for gas-solid circulation and is helpful for operating flexibly.

(2)

For each connection branch in a connection mode, the structure and distance from each cyclone to backpass should be close to each other, ensuring uniformity of branch resistance coefficient ξ_b,i distribution. It is helpful to diminish uneven solids suspension density distribution and solids circulation rates allocation.