An Embedded Half-Bridge Γ-Z-Source Inverter with Reduced Voltage Stress on Capacitors
Abstract
:1. Introduction
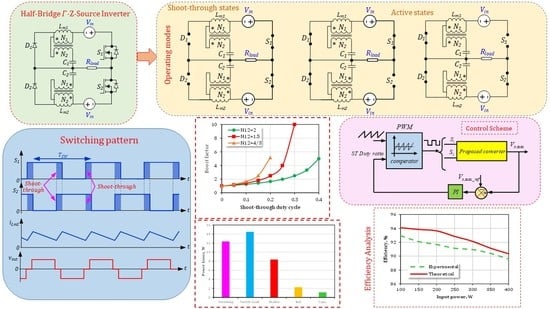
2. Proposed Topology
2.1. Operating Principle
- The series resistance and the voltage drop of the switches and the diodes are ignored;
- The series resistance and the capacitors and the inductors are ignored;
- The internal resistance of the input voltage is ignored;
- The switching method and the turning on and off of semiconductor elements are assumed to be ideal;
- The load of the proposed converter is pure ohmic with resistance R.
2.1.1. First Operating Mode
2.1.2. Second Operating Mode
2.1.3. Third Operating Mode
2.1.4. Fourth Operating Mode
2.2. Boost Factor
3. Design Considerations
4. Power Loss and THD Calculation
4.1. Power Loss Calculation
4.2. THD Calculation
5. Comparison
5.1. Comparison of Boost Factor
5.2. Comparison of Voltage Stress on Capacitors
5.3. Comparison of the Number of Used Elements
5.4. THD Comparison
6. Power Losses and Efficiency Evaluation
7. Simulation Results
8. Control Scheme and Dynamic Performance
9. Experimental Verification
10. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Peng, F.Z. Z-source inverter. IEEE Trans. Ind. Appl. 2003, 39, 504–510. [Google Scholar] [CrossRef]
- Anderson, J.; Peng, F. Four quasi-Z-source inverters. In Proceedings of the 2008 IEEE Power Electronics Specialists Conference, Rhodes, Greece, 15–19 June 2008; pp. 2743–2749. [Google Scholar]
- Tang, Y.; Xie, S.; Zhang, C. An improved Z-source inverter. IEEE Trans. Power Electron. 2010, 26, 3865–3868. [Google Scholar] [CrossRef]
- Babaei, E.; Asl, E.S. Steady-state analysis of high-voltage gain multiple series Z-source inverter. IET Power Electron. 2017, 10, 1518–1528. [Google Scholar] [CrossRef]
- Hasan Babayi Nozadian, M.; Babaei, E.; Hosseini, S.H.; Shokati Asl, E. Switched Z-Source Networks: A Review. IET Power Electron. 2019, 12, 1616–1633. [Google Scholar] [CrossRef]
- Ravindranath, A.; Mishra, S.K.; Joshi, A. Analysis and PWM control of switched boost inverter. IEEE Trans. Ind. Electron. 2013, 60, 5593–5602. [Google Scholar] [CrossRef]
- Nag, S.S.; Mishra, S. Current-fed switched inverter. IEEE Trans. Ind. Electron. 2014, 61, 4680–4690. [Google Scholar] [CrossRef]
- Babaei, E.; Shokati Asl, E.; Hasan Babayi, M.; Laali, S. Developed embedded switched-Z-source inverter. IET Power Electron. 2016, 9, 1828–1841. [Google Scholar] [CrossRef]
- Nozadian, M.H.B.; Babaei, E.; Hosseini, S.H.; Asl, E.S. Steady-state analysis and design considerations of high voltage gain switched Z-source inverter with continuous input current. IEEE Trans. Ind. Electron. 2017, 64, 5342–5350. [Google Scholar] [CrossRef]
- Zhang, G.; Li, Z.; Zhang, B.; Qiu, D.; Xiao, W.; Halang, W.A. A Z-source half-bridge converter. IEEE Trans. Ind. Electron. 2013, 61, 1269–1279. [Google Scholar] [CrossRef]
- Babaei, E.; Asl, E.S. A new topology for Z-source half-bridge inverter with low voltage stress on capacitors. Electr. Power Syst. Res. 2016, 140, 722–734. [Google Scholar] [CrossRef]
- Babaei, E.; Asl, E.S. High voltage gain half-bridge Z-source inverter with low voltage stress on capacitors. IEEE Trans. Ind. Electron. 2016, 64, 191–197. [Google Scholar] [CrossRef]
- Babaei, E.; Asl, E.S.; Babayi, M.H.; Nozadian, M.H.B. Steady-state and small-signal analysis of high-voltage gain half-bridge switched boost inverter. IEEE Trans. Ind. Electron. 2016, 63, 3546–3553. [Google Scholar] [CrossRef]
- Asl, E.S.; Babaei, E.; Sabahi, M. High voltage gain half-bridge quasi-switched boost inverter with reduced voltage stress on capacitors. IET Power Electron. 2017, 10, 1095–1108. [Google Scholar] [CrossRef]
- Asl, E.S.; Babaei, E.; Sabahi, M.; Nozadian, M.H.B.; Cecati, C. New half-bridge and full-bridge topologies for switched-boost inverter with continuous input current. IEEE Trans. Ind. Electron. 2017, 65, 3188–3197. [Google Scholar] [CrossRef]
- Asl, E.S.; Babaei, E.; Ranjbarizad, V.; Sabahi, M. A new topology for half-bridge Z-source inverter based on gamma structure. In Proceedings of the 2017 10th International Conference on Electrical and Electronics Engineering (ELECO), Bursa, Turkey, 30 November–2 December 2017; pp. 330–334. [Google Scholar]
- Qian, W.; Peng, F.Z.; Cha, H. Trans-Z-source inverters. IEEE Trans. Power Electron. 2011, 26, 3453–3463. [Google Scholar] [CrossRef]
- Chen, M.; Loh, P.C. A Single-Phase High Voltage-Gain Differential Y-Source Inverter. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 2027–2037. [Google Scholar] [CrossRef]
- Li, D.; Loh, P.C.; Zhu, M.; Gao, F.; Blaabjerg, F. Cascaded multicell trans-Z-source inverters. IEEE Trans. Power Electron. 2012, 28, 826–836. [Google Scholar]
- Nguyen, M.K.; Lim, Y.C.; Choi, J.H.; Choi, Y.O. Trans-switched boost inverters. IET Power Electron. 2016, 9, 1065–1073. [Google Scholar] [CrossRef]
- Nag, S.S.; Mishra, S. A coupled inductor based high boost inverter with sub-unity turns-ratio range. IEEE Trans. Power Electron. 2016, 31, 7534–7543. [Google Scholar] [CrossRef]
- Li, D.; Loh, P.C.; Zhu, M.; Gao, F.; Blaabjerg, F. Enhanced-boost Z-source inverters with alternate-cascaded switched- and tapped-inductor cells. IEEE Trans. Ind. Electron. 2012, 60, 3567–3578. [Google Scholar] [CrossRef]
- Babaei, E.; Bahador, A. Half-Bridge Trans-Z-Source Inverter with Continuous Input Current. In Proceedings of the 2021 12th Power Electronics, Drive Systems, and Technologies Conference (PEDSTC), Tabriz, Iran, 2–4 February 2021; pp. 1–6. [Google Scholar]
- Nozadian, M.H.B.; Babaei, E.; Hosseini, S.H. Effect of different PWM control methods on behavior of the series modified switched boost inverter. IET Power Electron. 2019, 12, 3041–3055. [Google Scholar] [CrossRef]
- Tang, Y.; Xie, S.; Zhang, C.; Xu, Z. Improved Z-source inverter with reduced Z-source capacitor voltage stress and soft-start capability. IEEE Trans. Power Electron. 2009, 24, 409–415. [Google Scholar] [CrossRef]
- Zhu, X.; Zhang, B.; Qiu, D. A New Half-Bridge Impedance Source Inverter with High Voltage Gain. IEEE Trans. Power Electron. 2018, 34, 3001–3008. [Google Scholar] [CrossRef]
















| Structures | Boost Factor | Maximum Voltage Stressacross of Capacitors |
|---|---|---|
| Proposed | ||
| ZSI [1] | ||
| QZSI [2] | ||
| IZSI [3] | ||
| Multiple SZSI [4] | ||
| SBI [6] | ||
| CFSI [7] | ||
| Switched inductor ESBI [8] | ||
| DA-SZSI [9] | ||
| Half-bridge ZSI [10] | ||
| Half-bridge SZSI [11] | ||
| Low-stress half-bridge ZSI [12] | ||
| Half-bridge SBI [13] | ||
| Half-bridge qSBI [14] | ||
| Diode-assisted half-bridge ZSI [15] | ||
| Trans ZSI [17] | ||
| Trans SBI [19] |
| Structures | Number of Elements | ||||
|---|---|---|---|---|---|
| Transformer. | L | C | D | S | |
| Proposed | 2 | - | 2 | 2 | 2 |
| ZSI [1] | - | 2 | 2 | 1 | 4 |
| QZSI [2] | - | 2 | 2 | 1 | 4 |
| IZSI [3] | - | 2 | 2 | 1 | 4 |
| Multiple SZSI [4] | - | N + 1 | 2N | N | 4 |
| SBI [6] | - | 1 | 1 | 2 | 5 |
| CFSI [7] | - | 1 | 1 | 2 | 5 |
| Switched inductor ESBI [8] | - | N | 1 | 3N − 1 | 5 |
| DA-SZSI [9] | - | 2 | 2 | 4 | 5 |
| Half-bridge ZSI [10] | - | 2 | 2 | 1 | 2 |
| Half-bridge SZSI [11] | - | 2N + 2 | 4N | 2N + 2 | 2 |
| Low-stress half-bridge ZSI [12] | - | N + 1 | 2N | N + 2 | 2 |
| Half-bridge SBI [13] | - | 2 | 2 | 4 | 4 |
| Half-bridge qSBI [14] | - | 2 | 2 | 4 | 4 |
| Diode-assisted half-bridge ZSI [15] | - | 1 | 2 | 4 | 4 |
| Trans ZSI [17] | 1 | - | 1 | 1 | 4 |
| Trans SBI [19] | 1 | - | 1 | 2 | 5 |
| Proposed Half-Bridge Inverter | [13] | [15] | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| B | THD% | B | THD% | B | THD% | B | THD% | B | THD% | |
| 0 | 1 | 40.89 | 1 | 41.19 | 1 | 41.19 | 1 | 40.33 | 1 | 41.71 |
| 0.05 | 1.11 | 38.92 | 1.18 | 39.34 | 1.25 | 39.34 | 1.12 | 40.17 | 1.18 | 37.9 |
| 0.1 | 1.25 | 33.3 | 1.43 | 33.78 | 1.67 | 33.78 | 1.29 | 34 | 1.43 | 33.79 |
| 0.15 | 1.43 | 26.98 | 1.82 | 27.05 | 2.5 | 27.04 | 1.55 | 27.39 | 1.82 | 27.22 |
| 0.2 | 1.67 | 21.92 | 2.5 | 21.97 | 5 | 21.89 | 2 | 22.45 | 2.5 | 23.61 |
| 0.25 | 2 | 21.14 | 4 | 21.15 | ----- | ----- | 3 | 23.63 | 4 | ----- |
| 0.3 | 2.5 | 22.4 | 10 | 22.5 | ----- | ----- | 7 | 28.75 | 10 | ----- |
| 0.4 | 5 | 28.39 | ----- | ----- | ----- | ----- | ----- | ----- | ----- | ----- |
| Parameter | Symbol | Value |
|---|---|---|
| Input voltage | Vi | 48 V |
| Switching frequency | fS | 10 kHZ |
| Load resistance | R | 100 Ω |
| Turns ratio | N12 | 4/3 |
| Magnetizing inductance | Lm | 2.5 mH |
| Capacitors | C | 100 µF |
| Shoot-through duty cycle | DST | 0.2 |
| Switches | S1, S2 | Cree C3M0120100K |
| Diodes | D1, D2 | Vishay VS-10ETS12THM3 |
| Equivalent resistance | rL | 395 mΩ |
| ESR of capacitors | rC | 6 mΩ |
| Drain-source on-state resistance | RDS | 141 mΩ |
| Rise time | ton | 15 ns |
| Fall time | toff | 8 ns |
| Forward voltage drop | VF,D | 1.1 V |
| Forward resistance | rD | 20 mΩ |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mashinchi Maheri, H.; Vinnikov, D.; Nozadian, M.H.B.; Shokati Asl, E.; Babaei, E.; Chub, A. An Embedded Half-Bridge Γ-Z-Source Inverter with Reduced Voltage Stress on Capacitors. Energies 2021, 14, 6433. https://doi.org/10.3390/en14196433
Mashinchi Maheri H, Vinnikov D, Nozadian MHB, Shokati Asl E, Babaei E, Chub A. An Embedded Half-Bridge Γ-Z-Source Inverter with Reduced Voltage Stress on Capacitors. Energies. 2021; 14(19):6433. https://doi.org/10.3390/en14196433
Chicago/Turabian StyleMashinchi Maheri, Hamed, Dmitri Vinnikov, Mohsen Hasan Babayi Nozadian, Elias Shokati Asl, Ebrahim Babaei, and Andrii Chub. 2021. "An Embedded Half-Bridge Γ-Z-Source Inverter with Reduced Voltage Stress on Capacitors" Energies 14, no. 19: 6433. https://doi.org/10.3390/en14196433
APA StyleMashinchi Maheri, H., Vinnikov, D., Nozadian, M. H. B., Shokati Asl, E., Babaei, E., & Chub, A. (2021). An Embedded Half-Bridge Γ-Z-Source Inverter with Reduced Voltage Stress on Capacitors. Energies, 14(19), 6433. https://doi.org/10.3390/en14196433