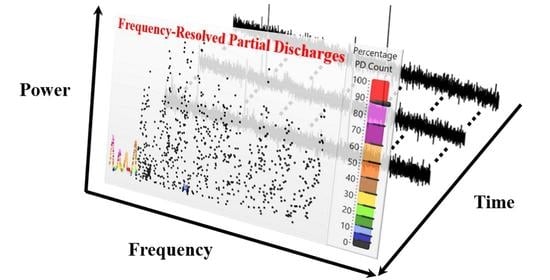
Frequency Resolved Partial Discharges Based on Spectral Pulse Counting
Abstract
:1. Introduction
2. Slot and Corona Discharges
Physics of Corona and Slot PDs
3. Discharges Due Sinusoidal Voltage Excitation
4. Frequency Resolved Partial Discharges (FRPD)
4.1. FRPD: Basic Concepts
4.2. Computer Implementation of FRPD
5. Experimental Measurements and Results
5.1. The Designed Golden Ratio Patch Antenna
5.2. Laboratory Setup
5.3. Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Antenna Design







References
- Stone, G. Condition Monitoring and Diagnostics of Motor and Stator Windings A Review. IEEE Trans. Dielectr. Electr. Insul. 2013, 20, 2073–2080. [Google Scholar] [CrossRef]
- Stone, G.C.; Culbert, I.; Boulter, E.A.; Dhirani, H. Electrical Insulation for Rotating Machines, 2nd ed.; Wiley: Hoboken, NJ, USA, 2004. [Google Scholar]
- Dehlinger, N.; Stone, G. Surface partial discharge in hydrogenerator stator windings: Causes, symptoms, and remedies. IEEE Electr. Insul. Mag. 2020, 36, 7–18. [Google Scholar] [CrossRef]
- Cselko, R.; Tamus, Z.A.; Szabo, A.; Berta, I. Comparison of acoustic and electrical partial discharge measurements on cable terminations. In Proceedings of the 2010 IEEE International Symposium on Electrical Insulation, San Diego, CA, USA, 6–9 June 2010; pp. 1–5. [Google Scholar] [CrossRef]
- Ilkhechi, H.D.; Samimi, M.H. Applications of the Acoustic Method in Partial Discharge Measurement: A Review. IEEE Trans. Dielectr. Electr. Insul. 2021, 28, 42–51. [Google Scholar] [CrossRef]
- IEC/TS60034-27-2. Rotating Electrical Machines—Part 27-2: On-line Partial Discharge Measurements on the Stator Winding Insulation of Rotating Electrical Machines, 1st ed.; International Electrotechnical Commission: Geneva, Switzerland, 2012. [Google Scholar]
- Araujo, R.C.F.; de Oliveira, R.M.S.; Brasil, F.S.; Barros, F.J.B. Novel Features and PRPD Image Denoising Method for Improved Single-Source Partial Discharges Classification in On-Line Hydro-Generators. Energies 2021, 14, 3267. [Google Scholar] [CrossRef]
- Yadam, Y.R.; Ramanujam, S.; Arunachalam, K. An Ultrawideband Conical Monopole With Radome for Detection of Partial Discharges. IEEE Sens. J. 2021, 21, 18764–18772. [Google Scholar] [CrossRef]
- Raymond, W.J.K.; Illias, H.A.; Bakar, A.H.A.; Mokhlis, H. Partial discharge classifications: Review of recent progress. Measurement 2015, 68, 164–181. [Google Scholar] [CrossRef] [Green Version]
- Luo, Y.; Li, Z.; Wang, H. A Review of Online Partial Discharge Measurement of Large Generators. Energies 2017, 10, 1694. [Google Scholar] [CrossRef] [Green Version]
- Lee, S.B.; Stone, G.C.; Antonino-Daviu, J.; Gyftakis, K.N.; Strangas, E.G.; Maussion, P.; Platero, C.A. Condition Monitoring of Industrial Electric Machines: State of the Art and Future Challenges. IEEE Ind. Electron. Mag. 2020, 14, 158–167. [Google Scholar] [CrossRef]
- Contin, A.; Montanari, G.; Ferraro, C. PD source recognition by Weibull processing of pulse height distributions. IEEE Trans. Dielectr. Electr. Insul. 2000, 7, 48–58. [Google Scholar] [CrossRef]
- Dey, D.; Chatterjee, B.; Chakravorti, S.; Munshi, S. Rough-granular approach for impulse fault classification of transformers using cross-wavelet transform. IEEE Trans. Dielectr. Electr. Insul. 2008, 15, 1297–1304. [Google Scholar] [CrossRef]
- Peng, X.; Wen, J.; Li, Z.; Yang, G.; Zhou, C.; Reid, A.; Hepburn, D.M.; Judd, M.D.; Siew, W.H. Rough set theory applied to pattern recognition of Partial Discharge in noise affected cable data. IEEE Trans. Dielectr. Electr. Insul. 2017, 24, 147–156. [Google Scholar] [CrossRef] [Green Version]
- Stone, G.; Culbert, I.; Bolter, E.; Dhirani, H. Electrical Insulation for Rotating Machines: Design, Evaluation, Aging, Testing, and Repair, 2nd ed.; IEEE Press: Piscataway, NJ, USA; Wiley: Hoboken, NJ, USA, 2014. [Google Scholar]
- Dakin, T.W. The Relation of Capacitance Increase with High Voltages to Internal Electric Discharges and Discharging Void Volume. Trans. Am. Inst. Electr. Eng. Part III Power Appar. Syst. 1959, 78, 790–794. [Google Scholar] [CrossRef]
- Fruth, B.; Niemeyer, L.; Hassig, M.; Fuhr, J.; Dunz, T. Phase Resolved Partial Discharge Measurements and Computer Aided Partial Discharge Analysis Performed on Different High Voltage Apparatus. In Proceedings of the Sixth Int. Symp. on High Voltage Engineering, 6th ISH, New Orleans, LA, USA, 28 August–1 September 1989; pp. 15.03–15.06. [Google Scholar]
- Oliveira, R.M.S.; Araujo, R.C.F.; Segundo, A.P.M.; Zampolo, R.F.; Fonseca, W.; Dmitriev, V.; Brasil, F.S. A System Based on Artificial Neural Networks for Automatic Classification of Hydro-generator Stator Windings Partial Discharges. J. Microwaves Optoelectron. Electromagn. Appl. 2017, 16, 628–645. [Google Scholar] [CrossRef] [Green Version]
- Hudon, C.; Belec, M. Partial Discharges Signal Interpretation for Generator Diagnostics. IEEE Trans. Dielectr. Electr. Insul. 2005, 12, 297–319. [Google Scholar] [CrossRef]
- Sako, H.; Mio, K.; Okada, S. Analysis of Phase Resolved Partial Discharge patterns with microstrip antenna. In Proceedings of the 2015 IEEE Electrical Insulation Conference (EIC), Seattle, WA, USA, 27 August 2015; pp. 346–357. [Google Scholar] [CrossRef]
- Bartnikas, R. Corona Discharge Processes in Voids. In Engineering Dielectrics: Corona Measurement and Interpretation, 2nd ed.; Bartinikas, R., Macmahon, E.J., Eds.; ASTM: West Conshohocken, PA, USA, 1979; Chapter 2; Volume 1. [Google Scholar]
- Raizer, Y.P. Gas Discharge Physics; Springer: Berlin/Heidelberg, Germany, 1991. [Google Scholar]
- Meek, J.M.; Craggs, J.D. Electrical Breakdown of Gases; Clarendon Press: Oxford, UK, 1953; pp. 251–290. [Google Scholar]
- Balanis, C.A. Advanced Engineering Eletromagnetics; John Wiley and Sons: New York, NY, USA, 1989. [Google Scholar]
- Eichwald, O.; Ducasse, O.; Dubois, D.; Abahazem, A.; Merbahi, N.; Benhenni, M.; Yousfi, M. Experimental analysis and modelling of positive streamer in air: Towards an estimation of O and N radical production. J. Phys. Appl. Phys. 2008. [Google Scholar] [CrossRef]
- Sigmond, R.S. The residual streamer channel: Return strokes and secondary streamers. J. Appl. Phys. 1984, 56, 1355–1370. [Google Scholar] [CrossRef]
- Huiskamp, T.; Sengers, W.; Beckers, F.J.C.M.; Nijdam, S.; Ebert, U.; van Heesch, E.J.M.; Pemen, A.J.M. Spatiotemporally resolved imaging of streamer discharges in air generated in a wire-cylinder reactor with (sub)nanosecond voltage pulses. Plasma Sources Sci. Technol. 2017, 26, 075009. [Google Scholar] [CrossRef] [Green Version]
- Hudson, G.G.; Loeb, L.B. Streamer Mechanism and Main Stroke in the Filamentary Spark Breakdown in Air as Revealed by Photomultipliers and Fast Oscilloscopic Techniques. Phys. Rev. 1961, 123, 1. [Google Scholar] [CrossRef]
- IEC60270. High Voltage Test Techniques—Partial Discharge Measurements, 3rd ed.; International Electrotechnical Commission—British Standard: London, UK, 2001. [Google Scholar]
- Schneider, K.; Farge, M. Wavelets: Mathematical Theory. In Encyclopedia of Mathematical Physics; Francoise, J.P., Naber, G.L., Tsun, T.S., Eds.; Academic Press: Oxford, UK, 2006; pp. 426–438. [Google Scholar] [CrossRef]
- Oliveira, R.M.S.; Modesto, J.F.M.; Dmitriev, V.; Brasil, F.S.; Vilhena, P.R.M. Spectral Method for Localization of Multiple Partial Discharges in Dielectric Insulation of Hydro-Generator Coils: Simulation and Experimental Results. J. Microwaves Optoelectron. Electromagn. Appl. 2016, 15, 170–190. [Google Scholar] [CrossRef] [Green Version]
- Sadiku, M. Elements of Electromagnetics, 3rd ed.; Oxford University Press: Oxford, UK, 2000. [Google Scholar]
- Yang, F.; Peng, C.; Yang, Q.; Luo, H.; Ullah, I.; Yang, Y. An UWB printed antenna for partial discharge UHF detection in high voltage switchgears. Prog. Electromagn. Res. C 2016, 69, 105–114. [Google Scholar] [CrossRef] [Green Version]
- Xavier, G.; Costa, E.; Serres, A.; Nobrega, L.; Oliveira, A.; Sousa, H. Design and Application of a Circular Printed Monopole Antenna in Partial Discharge Detection. IEEE Sens. J. 2019, 19, 3718–3725. [Google Scholar] [CrossRef]
- Zhang, Y.; Lazaridis, P.; Abd-Alhameed, R.; Glover, I. A compact wideband printed antenna for free-space radiometricdetection of partial discharge. Turk. J. Electr. Eng. Comput. Sci. 2017, 25, 1291–1299. [Google Scholar] [CrossRef] [Green Version]
- Dunlap, R.A. The Golden Ratio and Fibonacci Numbers; World Scientific Publishing Company: Toh Tuck Link, Singapore, 1998. [Google Scholar]
- Gupta, S.; Arora, T.; Singh, D.; Kumar Singh, K. Nature Inspired Golden Spiral Super-Ultra Wideband Microstrip Antenna. In Proceedings of the 2018 Asia-Pacific Microwave Conference (APMC), Kyoto, Japan, 6 November 2018; pp. 1603–1605. [Google Scholar] [CrossRef]
- Meena, A.; Garhwal, A.; Ray, K. Nature Inspired Fibonacci Sequence Microstrip Patch Antenna For Energy Harvesting Applications. Int. J. Recent Technol. Eng. (IJRTE) 2019, 8, 6154–6160. [Google Scholar]
- Tanabe, M.; Nakano, H. Low-Profile Wideband Spiral Antenna With a Circular HIS Reflector Composed of Homogenous Fan-Shaped Patch Elements. IEEE Trans. Antennas Propag. 2020, 68, 7219–7222. [Google Scholar] [CrossRef]
- Soboll, P.; Wienstroer, V.; Kronberger, R. Smooth Moves in Power Transition: New Yagi-Uda Antenna Design for Wireless Energy. IEEE Microw. Mag. 2016, 17, 75–80. [Google Scholar] [CrossRef]
- Balanis, C.A. Fundamental Parameters of Antennas. In Antenna Theory: Analysis and Design; Wiley-Interscience: Hoboken, NJ, USA, 2005; Chapter 2; pp. 27–132. [Google Scholar]



























Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sena, A.J.C.; de Oliveira, R.M.S.; do Nascimento, J.A.S. Frequency Resolved Partial Discharges Based on Spectral Pulse Counting. Energies 2021, 14, 6864. https://doi.org/10.3390/en14216864
Sena AJC, de Oliveira RMS, do Nascimento JAS. Frequency Resolved Partial Discharges Based on Spectral Pulse Counting. Energies. 2021; 14(21):6864. https://doi.org/10.3390/en14216864
Chicago/Turabian StyleSena, Anderson J. C., Rodrigo M. S. de Oliveira, and Júlio A. S. do Nascimento. 2021. "Frequency Resolved Partial Discharges Based on Spectral Pulse Counting" Energies 14, no. 21: 6864. https://doi.org/10.3390/en14216864
APA StyleSena, A. J. C., de Oliveira, R. M. S., & do Nascimento, J. A. S. (2021). Frequency Resolved Partial Discharges Based on Spectral Pulse Counting. Energies, 14(21), 6864. https://doi.org/10.3390/en14216864