Physically Motivated Water Modeling in Control-Oriented Polymer Electrolyte Membrane Fuel Cell Stack Models

Abstract

Polymer electrolyte membrane fuel cells (PEMFCs) are prone to membrane dehydration and liquid water flooding, negatively impacting their performance and lifetime. Therefore, PEMFCs require appropriate water management, which makes accurate water modeling indispensable. Unfortunately, available control-oriented models only replicate individual water-related aspects or use oversimplistic approximations. This paper resolves this challenge by proposing, for the first time, a control-oriented PEMFC stack model focusing on physically motivated water modeling, which covers phase change, liquid water removal, membrane water uptake, and water flooding effects on the electrochemical reaction. Parametrizing the resulting model with measurement data yielded the fitted model. The parameterized model delivers valuable insight into the water mechanisms, which were thoroughly analyzed. In summary, the proposed model enables the derivation of advanced control strategies for efficient water management and mitigation of the degradation phenomena of PEMFCs. Additionally, the model provides the required accuracy for control applications while maintaining the necessary computational efficiency.

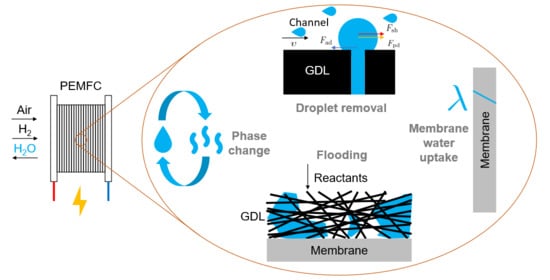
1. Introduction

Internal combustion engines will be superseded by more environmentally friendly alternatives in the future. Polymer electrolyte membrane fuel cells (PEMFCs) are a promising candidate in this regard, especially in mobile applications. Unfortunately, fuel-cell (FC)-driven vehicles still lead a niche existence in the vehicle market because of various challenges. One challenge is the optimal water management of PEMFCs, which is critical for efficient operation [1], on the one hand, to guarantee a sufficiently hydrated membrane at all times and, on the other hand, to minimize the amount of internal liquid water. The latter leads to another challenge: extending the lifetime of FCs, which could be negatively affected by liquid water [2]. Further challenges are FC development and the related experimental expenditures, which are costly, but reducible by utilizing simulations instead. A significant contribution to resolve the named and other challenges is to develop a suitable FC model that can reproduce the essential water-related transient mechanisms. Accurate replication of the internal water dynamics is crucial for, e.g., diagnosing bad operating conditions such as membrane dehydration, simulation of various operating strategies to determine liquid water flooding, and controlling PEMFCs to increase efficiency by guaranteeing optimal water-related conditions.

On the one hand, control-oriented models usually have a low spatial order and are simplified in many aspects to obtain the necessary computational efficiency for real-time control applications. On the other hand, they still have to replicate the real process with sufficient accuracy to provide satisfactory application results [2,3,4]. The available models in the literature cover a wide variety of complexity and accuracy regarding water-related modeling, starting from neglecting liquid water inside the model to the point of spatially distributed water modeling. These circumstances influence the ability of the models to replicate the water dynamics, which is essential as outlined above. For example, a PEMFC model to predict the system’s thermal dynamics under the assumption of no water storage inside the system was presented in [5]. This assumption allows the determination of the mass flow of liquid water exiting the FC using a mass balance. The latter considers the generated, incoming, and outgoing water in the gaseous and liquid state. In comparison, in [6], it was assumed that liquid water does not leave the FC stack. It will either evaporate or accumulate inside. Furthermore, it was assumed that the amount of water exceeding the mass of vapor at the vapor saturation pressure would instantaneously condensate into liquid water and vice versa. In addition to that, the entrainment of liquid water by the gas stream was modeled in [7]. The outgoing flow of liquid water was calculated by multiplying the mass of liquid water inside the manifold with a constant and the exiting mass flow. A different approach was followed in [8]. Here, it was assumed that the gaseous and liquid phases inside the channels have the same velocity, and from this assumption, the outgoing liquid water flow was derived. Unlike the other models, the water condensation and evaporation were determined with a finite-rate phase change. The modeling principles used in [8] are common for control-oriented models, e.g., in [9,10], similar ones were utilized. A catalyst layer (CL) volume on the cathode side to replicate the diffusion process through the gas diffusion layer (GDL) was introduced in [11]. This approach has the advantage that the properties at the CL are now evaluable, e.g., the water activity at the CL, which is higher than the water activity in the lumped cathode volume due to the electrochemical reaction. In [12], the GDL was additionally discretized on the cathode and anode side into multiple volumes. Depending on the actual FC temperature, the membrane water content was determined by linearly interpolating between two temperature-specific functions compared to the other models. Furthermore, water flooding effects on the electrochemical reaction were considered by reducing the apparent FC area and, in the following, increasing the apparent current density in the nonflooded sections of the CL. In [13], a similar approach was utilized on an FC with a single cell. Here, the membrane, the GDL of the cathode and anode, and the channels of the cathode and anode were discretized in the through-plane direction, whereas the cathode and anode CLs were modeled with a lumped modeling ansatz. The modeling framework considered the phase change, liquid water transport, droplet detachment, gaseous transport in GDLs and channels, and the flooding effects in the channels, GDLs, and CLs of the FC. The modeling basis allows for additional discretization along the channels, resulting in a one-dimensional plus one-dimensional dimensionality of the model. However, this additional discretization results in a significantly increased computational burden. In [14], a lumped parameter model with a one-dimensional membrane electrode assembly submodel was proposed. The effects of flooding were also modeled, but instead of using the apparent FC area and current density, the liquid water saturation in the GDL was utilized. As outlined here, many PEMFC models exist, which cover the water-related mechanisms at different complexity and accuracy levels. The phase change is not considered, or an instantaneous or approximated finite-rate phase change is used. Moreover, it is common to use a function determined at 30 ${}^{°}\mathrm{C}$ to calculate the membrane water content, which is lower than most nominal FC operating temperatures. Furthermore, it was assumed that liquid water accumulates inside the FC or is continuously removed by some approximations depending on the gas stream. In addition, only very few control-oriented models capture flooding effects on the electrochemical model, essential during high loads and for minimizing degradation. Above all, most available models in the literature only consider individual water-related aspects, and a model of the FC stack having all significant water effects incorporated in a physically motivated way is not available. In summary, there is a knowledge gap regarding control-oriented models for real-time applications, which can replicate the real water dynamics in an FC stack acceptably.

Compared to existing models, this work proposes a novel control-oriented model including the main water mechanisms in a physically motivated way to bridge the named knowledge gap for the first time. The included mechanisms are the phase change, droplet removal, membrane water uptake, and flooding effects. An adapted Hertz–Knudsen equation governs the phase change, and droplet detachment is determinable by evaluating the forces acting on a droplet. These two approaches are unique in control-oriented models and enable realistic modeling of the transients correlated with the phase change and liquid water removal. Furthermore, the membrane water uptake is obtainable with a function determined at the nominal FC operating temperature and using the approximated properties at the GDL. This work additionally used effective medium theory (EMT) to consider flooding effects on the electrochemical reaction. An experimental PEMFC stack test bench delivered the measurement data for parameterization and validation, and the tuned parameters were obtained by conducting the parametrization of the resulting model. The model provides sufficient accuracy for control applications, while maintaining the necessary computational efficiency. The novelties are that the model can replicate the internal transient water mechanisms and deliver accurate internal water states, unlike present models. The capability to replicate flooding and dry-out operating conditions opens the possibility of more precise modeling, not only during transient operating conditions, but also during startup and shutdown sequences. The latter enables the calculation of all the main degradation prerequisites under this kind of operation, thus allowing the derivation of predictive control strategies to mitigate degradation phenomena and improve water management, which gives an outlook for further work.

This work is subsequently structured as follows: Section 2 shows the description of the PEMFC model. This section also contains a short overview of the experimental setup and the model parametrization. Moreover, Section 3 gives the obtained results, including a thorough discussion.

2. Fuel Cell Model

This section shows the description of the control-oriented PEMFC stack model focusing on the physically motivated water modeling. Later in this section, a short description of the experimental setup and the model parametrization is given. The model from Ritzerberger et al. [10], which built on Pukrushpan et al.’s [6] work, was the basis for the proposed model. The choice fell on the named model because it has the advantageous property of analytical differentiability, which is beneficial for various control applications [15,16,17]. The model derivation was conducted based on the following assumptions:

• The respective FC manifolds are lumped into one volume and do not have any spatial expansion;
• The gases are ideal;
• The gas inside a manifold has homogeneous properties;
• The gas in the exit manifold has the same composition as in the center manifold;
• Dry air only consists of nitrogen and oxygen;
• The FC has one uniform and externally controlled temperature;
• Steady-state conditions always hold in the supply and exit manifolds, as well as the GDL.

The model consists of four interconnected submodels: the cathode, anode, membrane, and electrochemical submodel, illustrated in Figure 1.

2.1. Model Description

2.1.1. Cathode

The cathode submodel consists of three consequently connected volumes: the supply, center, and exit manifold. Linearized nozzle equations, e.g.,

$${\dot{m}}_{\mathrm{ca},\mathrm{in}}={\dot{m}}_{\mathrm{ca},\mathrm{cm},\mathrm{sm}}=k_{\mathrm{ca},\mathrm{cm},\mathrm{sm}}(p_{\mathrm{ca},\mathrm{sm}}-p_{\mathrm{ca},\mathrm{cm}}),$$

(1)

interconnect these manifolds. In this equation, ${\dot{m}}_{\mathrm{ca},\mathrm{in}}$ denotes the humid air inflow into the stack, ${\dot{m}}_{\mathrm{ca},\mathrm{cm},\mathrm{sm}}$ the mass flow between the supply and center manifold, $k_{\mathrm{ca},\mathrm{cm},\mathrm{sm}}$ the corresponding nozzle coefficient, $p_{\mathrm{ca},\mathrm{sm}}$ the supply manifold pressure, and $p_{\mathrm{ca},\mathrm{cm}}$ the center manifold pressure. The only unknown is the supply manifold pressure, which is explicitly expressible by transforming the given equation. A nonlinear nozzle equation deduced from the Bernoulli equation describes the outflow from the exit manifold to the atmosphere because a linearized nozzle equation cannot replicate the nonlinear behavior due to the significant pressure differences:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\dot{m}}_{\mathrm{ca},\mathrm{em},\mathrm{cm}}& ={\dot{m}}_{\mathrm{ca},\mathrm{atm},\mathrm{em}},\hfill \\ \hfill k_{\mathrm{ca},\mathrm{em},\mathrm{cm}}(p_{\mathrm{ca},\mathrm{cm}}-p_{\mathrm{ca},\mathrm{em}})& ={\alpha }_{\mathrm{ca}}{k}_{\mathrm{ca},\mathrm{atm},\mathrm{em}}\sqrt{2{\rho }_{\mathrm{ca}}(p_{\mathrm{ca},\mathrm{em}}-p_{\mathrm{atm}})}.\hfill \end{array}\end{array}$$

(2)

In Equation (2), ${\dot{m}}_{\mathrm{ca},\mathrm{em},\mathrm{cm}}$ denotes the mass flow between the center and exit manifold and ${\dot{m}}_{\mathrm{ca},\mathrm{atm},\mathrm{em}}$ the one between the exit manifold and the atmosphere. Furthermore, k is the respective nozzle coefficient, p the pressure, ${\alpha }_{\mathrm{ca}}$ the valve position, ${\rho }_{\mathrm{ca}}=m_{\mathrm{ca}}/V_{\mathrm{ca}}$ the density of the cathode gas, $m_{\mathrm{ca}}={\sum }_i{m}_{\mathrm{ca},i}$ for $i\in \{{\mathrm{O}}_2,{\mathrm{N}}_2,\mathrm{vap}\}$ the summed mass of the cathode species $m_{\mathrm{ca},i}$, $V_{\mathrm{ca}}$ the lumped cathode volume, and vap vapor. Here, the cathode exit manifold pressure $p_{\mathrm{ca},\mathrm{em}}$ is the only unknown, which is again expressible by transforming the equation. Using the ideal gas law:

$$p_{\mathrm{ca},i}=\frac{\mathcal{R}T}{V_{\mathrm{ca}}}\frac{m_{\mathrm{ca},i}}{M_i}$$

(3)

yields the respective partial pressures $p_{\mathrm{ca},i}$ in the center manifold. Here, $\mathcal{R}$ denotes the universal gas constant, T the FC temperature, and $M_i$ the molar mass of i. The absolute pressure in the center manifold is the sum of all partial pressures $p_{\mathrm{ca},\mathrm{cm}}={\sum }_i{p}_{\mathrm{ca},i}$.

The respective mass balances:

$${\dot{m}}_{\mathrm{ca},i}={\dot{m}}_{\mathrm{ca},\mathrm{cm},\mathrm{sm}}{w}_{\mathrm{ca},\mathrm{sm},i}+{\dot{m}}_{\mathrm{ca},\mathrm{s},i}-{\dot{m}}_{\mathrm{ca},\mathrm{em},\mathrm{cm}}{w}_{\mathrm{ca},\mathrm{cm},i}$$

(4)

describe the change of the species over time. Here, ${\dot{m}}_{\mathrm{ca},\mathrm{s},i}$ is the sink and source term, $w_{\mathrm{ca},\mathrm{cm},i}=m_{\mathrm{ca},i}/m_{\mathrm{ca}}$ the mass fraction of species i in the center manifold, and $w_{\mathrm{ca},\mathrm{sm},i}$ the mass fraction of species i in the supply manifold. The humidity ratio of the inlet air:

$$x_{\mathrm{ca},\mathrm{in}}=\frac{M_{\mathrm{vap}}}{M_{\mathrm{air}}}\frac{{\phi }_{\mathrm{ca},\mathrm{in}}{p}_{\mathrm{sat}}}{p_{\mathrm{ca},\mathrm{sm}}-{\phi }_{\mathrm{ca},\mathrm{in}}{p}_{\mathrm{sat}}}$$

(5)

is necessary to determine the fractions of the inflowing species. Here, $M_{\mathrm{air}}$ denotes the molar mass of dry air, ${\phi }_{\mathrm{ca},\mathrm{in}}$ the relative humidity of the inflowing air, and $p_{\mathrm{sat}}=p_{\mathrm{sat}}\left(T\right)$ the vapor saturation pressure as a function of temperature [19]. The mass fraction of dry air in the humid inflowing air is $w_{\mathrm{ca},\mathrm{in},\mathrm{air}}=1/(1+x_{\mathrm{ca},\mathrm{in}})$. Using the given quantities, the respective mass fractions and sink and source terms are derivable:

$$\begin{array}{cccccc}\hfill {\mathrm{O}}_2& :\hfill & \hfill w_{\mathrm{ca},\mathrm{sm},{\mathrm{O}}_2}& =w_{\mathrm{ca},\mathrm{in},\mathrm{air}}{w}_{\mathrm{air},{\mathrm{O}}_2},\hfill & \hfill {\dot{m}}_{\mathrm{ca},\mathrm{s},{\mathrm{O}}_2}& =-\frac{I{M}_{{\mathrm{O}}_2}{n}_{\mathrm{cell}}}{4\mathcal{F}},\hfill \end{array}$$

(6)

$$\begin{array}{cccccc}\hfill {\mathrm{N}}_2& :\hfill & \hfill w_{\mathrm{ca},\mathrm{sm},{\mathrm{N}}_2}& =w_{\mathrm{ca},\mathrm{in},\mathrm{air}}{w}_{\mathrm{air},{\mathrm{N}}_2},\hfill & \hfill {\dot{m}}_{\mathrm{ca},\mathrm{s},{\mathrm{N}}_2}& =-{\dot{m}}_{\mathrm{m},{\mathrm{N}}_2},\hfill \end{array}$$

(7)

$$\begin{array}{cccccc}\hfill \mathrm{vap}& :\hfill & \hfill w_{\mathrm{ca},\mathrm{sm},\mathrm{vap}}& =1-w_{\mathrm{ca},\mathrm{in},\mathrm{air}},\hfill & \hfill {\dot{m}}_{\mathrm{ca},\mathrm{s},\mathrm{vap}}& =\frac{I{M}_{\mathrm{vap}}{n}_{\mathrm{cell}}}{2\mathcal{F}}+{\dot{m}}_{\mathrm{m},\mathrm{vap}}-{\dot{m}}_{\mathrm{ca},\mathrm{phase}}.\hfill \end{array}$$

(8)

In Equations (6)–(8), $w_{\mathrm{air},{\mathrm{O}}_2}$ and $w_{\mathrm{air},{\mathrm{N}}_2}=\left(1-w_{\mathrm{air},{\mathrm{O}}_2}\right)$ denote the mass fraction of oxygen and nitrogen in dry air, respectively, I the current, $n_{\mathrm{cell}}$ the number of cells, $\mathcal{F}$ the Faraday constant, ${\dot{m}}_{\mathrm{ca},\mathrm{phase}}$ the phase change rate, ${\dot{m}}_{\mathrm{m},\mathrm{vap}}$ the vapor flow through the membrane, and ${\dot{m}}_{\mathrm{m},{\mathrm{N}}_2}$ the nitrogen flow through the membrane. The derivation of the latter two follows in Section 2.1.3. The consumed oxygen due to the electrochemical reaction governs the mass balance (6), and the first term of the mass balance (8) describes the produced water during the reaction. The equation:

$${\dot{m}}_{\mathrm{ca},\mathrm{liq}}={\dot{m}}_{\mathrm{ca},\mathrm{phase}}-{\dot{m}}_{\mathrm{ca},\mathrm{liq},\mathrm{out}}$$

(9)

describes the change of liquid water in the cathode, where ${\dot{m}}_{\mathrm{ca},\mathrm{liq},\mathrm{out}}$ is the liquid water removal rate.

An adapted Hertz–Knudsen equation with a Langmuir-like type of correction addressing the hysteresis between the condensation and evaporation:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\dot{m}}_{\mathrm{ca},\mathrm{phase}}& =k_{\mathrm{phase}}\sqrt{\frac{M_{\mathrm{vap}}}{2\pi \mathcal{R}T}}(p_{\mathrm{ca},\mathrm{GDL},\mathrm{vap}}-p_{\mathrm{sat}})|{\mathsf{\Phi }}_{\mathrm{ca},\mathrm{phase}}-s_{\mathrm{ca}}|,\hfill \\ \hfill {\mathsf{\Phi }}_{\mathrm{ca},\mathrm{phase}}& =\left\{\begin{array}{c}1,p_{\mathrm{ca},\mathrm{GDL},\mathrm{vap}}\ge p_{\mathrm{sat}}\hfill \\ 0,p_{\mathrm{ca},\mathrm{GDL},\mathrm{vap}}<p_{\mathrm{sat}}\hfill \end{array}\right.\hfill \end{array}\end{array}$$

(10)

governs the phase change rate. Here, $k_{\mathrm{phase}}$ is the phase change coefficient, $p_{\mathrm{ca},\mathrm{GDL},\mathrm{vap}}=p_{\mathrm{ca},\mathrm{vap}}(1+2I/I_{\mathrm{ca},\mathrm{lm}})$ the approximated vapor partial pressure at the GDL [20,21], $I_{\mathrm{ca},\mathrm{lm}}$ the cathode limit current, ${\mathsf{\Phi }}_{\mathrm{ca},\mathrm{phase}}$ the phase change switching function, $s_{\mathrm{ca}}=m_{\mathrm{ca},\mathrm{liq}}/\left({\rho }_{\mathrm{liq}}{V}_{\mathrm{ca}}\right)$ the liquid water saturation, and ${\rho }_{\mathrm{liq}}$ the liquid water density. Section 2.1.4 contains a detailed discussion about the limit current. The vapor partial pressure in the cathode volume $p_{\mathrm{ca},\mathrm{vap}}$ is not suitable to determine the phase change rate because the partial pressure at the GDL and CL interface $p_{\mathrm{ca},\mathrm{GDL},\mathrm{vap}}$ is much higher during load. Therefore, phase change dominantly takes place in the GDL, where the concentration of the gaseous water is the highest. Instead of implementing additional GDL states to the model, a steady-state approximation delivers the wanted quantity. This approach has the advantage of more accurate modeling while maintaining the computational efficiency of the model. Furthermore, the absolute value expression with a differentiable switching function [11] scales the phase change rate. If the vapor partial pressure is above the saturation pressure, condensation occurs, and the scaling expression is $\left(1-s_{\mathrm{ca}}\right)$, which is physically interpretable as the available surface on which condensation can occur. In the opposite case, the scaling expression is only $s_{\mathrm{ca}}$, which means the actual amount of liquid water is scaling the phase change rate. Compared to approaches with instantaneous phase changes, finite-rate modeling avoids numerical difficulties and discontinuities, as it serves as a relaxation factor.

It is common to model the liquid water removal rate proportional to the outflowing gas, which means droplet removal happens continuously. However, in this work, a force balance on an average droplet, similar to the one proposed in [13], was used to determine when it detaches, and only if detachment occurs, liquid water is removed. This way, a discrete approach for the liquid water removal was utilized, which causes fluctuations in the availability of the reactants and consequential the voltage output, as seen from several experimental studies, e.g., [22]. Figure 2 shows the forces acting on a droplet, which visualizes the utilized physical approach.

The geometry of an average droplet is necessary to calculate the acting forces. The reduced water saturation:

$$s_{\mathrm{ca},\mathrm{red}}=\frac{s_{\mathrm{ca}}-s_{\mathrm{im}}}{1-s_{\mathrm{im}}},s_{\mathrm{ca},\mathrm{red}}\in [0,1]$$

(11)

governs the average droplet geometry [23]. Here, $s_{\mathrm{im}}$ denotes the immobile water saturation. The latter considers that a sufficient amount of liquid water must accumulate in the GDL before individual droplets connect into streams flowing the liquid water to the GDL–channel interface, where individual droplets are formed. Solely the water on the GDL surface and in the cathode channels, respectively, is prone to droplet removal. A saturation function [11] ensures compliance with the given limits. Multiplying the reduced water saturation $s_{\mathrm{ca},\mathrm{red}}$ with the lumped cathode volume $V_{\mathrm{ca}}$ and dividing it by the number of droplet injection points $n_{\mathrm{inj}}$, the number of cells $n_{\mathrm{cell}}$, and the FC area $A_{\mathrm{cell}}$ yield the average droplet volume:

$$V_{\mathrm{ca},\mathrm{dr}}=\frac{s_{\mathrm{ca},\mathrm{red}}{V}_{\mathrm{ca}}}{n_{\mathrm{inj}}{n}_{\mathrm{cell}}{A}_{\mathrm{cell}}}.$$

(12)

The single-sized droplets were utilized due to the fact that taking into account different sizes of droplets would be computationally too demanding to calculate in these applications. The number of injection points and thus individual droplets formed per area [24] is obtained with:

$$n_{\mathrm{inj}}=\left(16.67\mathrm{erf}\left(3.328\left(\frac{I}{A_{\mathrm{cell}}}-1.097\right)\right)+19.8\right){10}^6,$$

(13)

where $\mathrm{erf}$ is the error function (a special sigmoid function). The average droplet radius is a geometric relation given by:

$$r_{\mathrm{ca}}=\sqrt[3]{\frac{V_{\mathrm{ca},\mathrm{dr}}}{\pi \left(\frac{2}{3}+\frac{{cos}^3\left({\theta }_{\mathrm{w}}\right)}{3}-cos\left({\theta }_{\mathrm{w}}\right)\right)}},$$

(14)

where ${\theta }_{\mathrm{w}}$ is the wetting angle. The height $h_{\mathrm{ca}}$ and the wetted diameter $d_{\mathrm{ca}}$ of the average droplet are determinable by:

$$\begin{array}{cc}\hfill h_{\mathrm{ca}}& =r_{\mathrm{ca}}(1+cos(\pi -{\theta }_{\mathrm{w}})),\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill d_{\mathrm{ca}}& =2r_{\mathrm{ca}}cos\left({\theta }_{\mathrm{w}}-\frac{\pi }{2}\right).\hfill \end{array}$$

(16)

The adhesion $F_{\mathrm{ca},\mathrm{ad}}$, pressure drop $F_{\mathrm{ca},\mathrm{pd}}$, shear $F_{\mathrm{ca},\mathrm{sh}}$, and gravitational force $F_{\mathrm{ca},\mathrm{g}}$ [25,26] are expressed as:

$$\begin{array}{cc}\hfill F_{\mathrm{ca},\mathrm{ad}}& =\gamma d_{\mathrm{ca}}\beta (cos({\theta }_{\mathrm{w}}-{\theta }_{\mathrm{sl}})-cos({\theta }_{\mathrm{w}}+{\theta }_{\mathrm{sl}})),\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill F_{\mathrm{ca},\mathrm{pd}}& =\frac{4r_{\mathrm{ca}}^2{\kappa }_{\mathrm{ca}}{\mu }_{\mathrm{ca}}{\dot{V}}_{\mathrm{ca},\mathrm{ch}}}{W_{\mathrm{ca}}{H}_{\mathrm{ca}}^2},{\kappa }_{\mathrm{ca}}=12{\left(1-\frac{192H_{\mathrm{ca}}}{{\pi }^5{W}_{\mathrm{ca}}}tanh\left(\frac{\pi W_{\mathrm{ca}}}{2H_{\mathrm{ca}}}\right)\right)}^{-1},\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill F_{\mathrm{ca},\mathrm{sh}}& =\frac{24r_{\mathrm{ca}}^2{\mu }_{\mathrm{ca}}{H}_{\mathrm{ca}}{v}_{\mathrm{ca},\mathrm{ch}}}{{(H_{\mathrm{ca}}-h_{\mathrm{ca}})}^2},\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill F_{\mathrm{ca},\mathrm{g}}& =V_{\mathrm{ca},\mathrm{dr}}{\rho }_{\mathrm{liq}}g\hfill \end{array}$$

(20)

with the calculated quantities. Here, $\gamma$ denotes surface tension, $\beta$ and ${\kappa }_{\mathrm{ca}}$ parameters, ${\theta }_{\mathrm{sl}}$ the sliding angle, ${\mu }_{\mathrm{ca}}$ the dynamic viscosity of the gas, ${\dot{V}}_{\mathrm{ca},\mathrm{ch}}$ the volume flow per channel, $W_{\mathrm{ca}}$ and $H_{\mathrm{ca}}$ the channel width and height, respectively, $v_{\mathrm{ca},\mathrm{ch}}={\dot{V}}_{\mathrm{ca},\mathrm{ch}}/\left(W_{\mathrm{ca}}{H}_{\mathrm{ca}}\right)$ the bulk gas velocity in a channel, and g the gravitational acceleration. The volume flow per channel:

$${\dot{V}}_{\mathrm{ca},\mathrm{ch}}=\frac{{\dot{m}}_{\mathrm{ca},\mathrm{cm},\mathrm{sm}}}{{\rho }_{\mathrm{ca}}{n}_{\mathrm{cell}}{n}_{\mathrm{ca},\mathrm{ch}}(1-s_{\mathrm{ca},\mathrm{red}})}$$

(21)

is derived by dividing the mass flow into the center manifold ${\dot{m}}_{\mathrm{ca},\mathrm{cm},\mathrm{sm}}$ by the cathode gas density ${\rho }_{\mathrm{ca}}$, the number of cells $n_{\mathrm{cell}}$, and the number of channels per cell $n_{\mathrm{ca},\mathrm{ch}}$ and correcting it with the reduced cross-section $\left(1-s_{\mathrm{ca},\mathrm{red}}\right)$. Figure 2 shows the direction of action of the respective forces. Therefore, the shear, pressure drop, and gravitational force are summarizable into a pushing force ${\overrightarrow{F}}_{\mathrm{ca},\mathrm{push}}={\overrightarrow{F}}_{\mathrm{ca},\mathrm{sh}}+{\overrightarrow{F}}_{\mathrm{ca},\mathrm{pd}}+{\overrightarrow{F}}_{\mathrm{ca},\mathrm{g}}$. The directional gravitational force is dependent on the FC orientation, but it is negligible for typical droplet sizes [27]. Therefore, it is not sketched in the figure and is only given for the sake of completeness. Under the assumption that the droplet removal rate is proportional to the average droplet weight, the relation:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\dot{m}}_{\mathrm{ca},\mathrm{liq},\mathrm{out}}& =k_{\mathrm{liq}}{\rho }_{\mathrm{liq}}{V}_{\mathrm{ca},\mathrm{dr}}{\mathsf{\Phi }}_{\mathrm{ca},\mathrm{liq}},\hfill \\ \hfill {\mathsf{\Phi }}_{\mathrm{ca},\mathrm{liq}}& =\left\{\begin{array}{c}1,F_{\mathrm{ca},\mathrm{push}}>F_{\mathrm{ca},\mathrm{ad}}\hfill \\ 0,F_{\mathrm{ca},\mathrm{push}}\le F_{\mathrm{ca},\mathrm{ad}}\hfill \end{array}\right.\hfill \end{array}\end{array}$$

(22)

is derived, where $k_{\mathrm{liq}}$ is the droplet-removal coefficient and ${\mathsf{\Phi }}_{\mathrm{ca},\mathrm{liq}}$ the droplet-removal switching function. The latter makes sure that droplet removal only takes place when the pushing force exceeds the adhesion force.

2.1.2. Anode

The anode submodel has a similar structure as the cathode one. This section highlights the main differences. Compared to the cathode, the anode has an additional recirculation path. Therefore, the mass balance to determine the exit manifold pressure $p_{\mathrm{an},\mathrm{em}}$ additionally considers the recirculation mass flow ${\dot{m}}_{\mathrm{an},\mathrm{reci}}$ (derived from the ideal gas law) at the outlet side:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\dot{m}}_{\mathrm{an},\mathrm{em},\mathrm{cm}}& ={\dot{m}}_{\mathrm{an},\mathrm{atm},\mathrm{em}}+{\dot{m}}_{\mathrm{an},\mathrm{reci}},\hfill \\ \hfill k_{\mathrm{an},\mathrm{em},\mathrm{cm}}(p_{\mathrm{an},\mathrm{cm}}-p_{\mathrm{an},\mathrm{em}})& ={\alpha }_{\mathrm{an}}{k}_{\mathrm{an},\mathrm{atm},\mathrm{em}}\sqrt{2{\rho }_{\mathrm{an}}(p_{\mathrm{an},\mathrm{em}}-p_{\mathrm{atm}})}+\frac{p_{\mathrm{an},\mathrm{em}}{\dot{V}}_{\mathrm{an},\mathrm{reci}}}{{\mathcal{R}}_{\mathrm{an}}T}.\hfill \end{array}\end{array}$$

(23)

Here, ${\mathcal{R}}_{\mathrm{an}}$ denotes the anode mass-specific gas constant and ${\dot{V}}_{\mathrm{an},\mathrm{reci}}=k_{\mathrm{an},\mathrm{reci}}{P}_{\mathrm{an},\mathrm{reci}}$ the recirculation volume flow. The latter is not measured directly, but assumed to be proportional to the measured recirculation pump power $P_{\mathrm{an},\mathrm{reci}}$. The anode mass-specific gas constant is obtained from:

$${\mathcal{R}}_{\mathrm{an}}=\frac{\mathcal{R}}{m_{\mathrm{an}}}\sum _i\frac{m_{\mathrm{an},i}}{M_i}\mathrm{for}i\in \{{\mathrm{H}}_2,{\mathrm{N}}_2,\mathrm{vap}\}.$$

(24)

In Equation (23), only the exit manifold pressure $p_{\mathrm{an},\mathrm{em}}$ is unknown, which is now expressible by transforming the equation. A linearized nozzle equation delivers the mass flow from the supply to the center manifold ${\dot{m}}_{\mathrm{an},\mathrm{cm},\mathrm{sm}}$ at the inlet side. Note that the supply manifold pressure $p_{\mathrm{an},\mathrm{sm}}$ is a model input, and thus, the anode is pressure driven. This configuration has the advantage of stable model dynamics during closed-end anode operations. The anode inflow is obtainable from the relation ${\dot{m}}_{\mathrm{an},\mathrm{in}}={\dot{m}}_{\mathrm{an},\mathrm{cm},\mathrm{sm}}-{\dot{m}}_{\mathrm{an},\mathrm{reci}}$.

Moreover, the mass fractions and sink and source terms differ from the cathode:

$$\begin{array}{ccc}\hfill {\mathrm{H}}_2& :\hfill & \hfill \begin{array}{cc}\hfill w_{\mathrm{an},\mathrm{sm},{\mathrm{H}}_2}& =\frac{w_{\mathrm{an},\mathrm{in},{\mathrm{H}}_2}{\dot{m}}_{\mathrm{an},\mathrm{in}}+w_{\mathrm{an},\mathrm{cm},{\mathrm{H}}_2}{\dot{m}}_{\mathrm{an},\mathrm{reci}}}{{\dot{m}}_{\mathrm{an},\mathrm{cm},\mathrm{sm}}},\hfill \\ \hfill {\dot{m}}_{\mathrm{an},\mathrm{s},{\mathrm{H}}_2}& =-\frac{I{M}_{{\mathrm{H}}_2}{n}_{\mathrm{cell}}}{2\mathcal{F}},\hfill \end{array}\end{array}$$

(25)

$$\begin{array}{ccc}\hfill {\mathrm{N}}_2& :\hfill & \hfill \begin{array}{cc}\hfill w_{\mathrm{an},\mathrm{sm},{\mathrm{N}}_2}& =\frac{w_{\mathrm{an},\mathrm{cm},{\mathrm{N}}_2}{\dot{m}}_{\mathrm{an},\mathrm{reci}}}{{\dot{m}}_{\mathrm{an},\mathrm{cm},\mathrm{sm}}},\hfill \\ \hfill {\dot{m}}_{\mathrm{an},\mathrm{s},{\mathrm{N}}_2}& ={\dot{m}}_{\mathrm{m},{\mathrm{N}}_2},\hfill \end{array}\end{array}$$

(26)

$$\begin{array}{ccc}\hfill \mathrm{vap}& :\hfill & \hfill \begin{array}{cc}\hfill w_{\mathrm{an},\mathrm{sm},\mathrm{vap}}& =\frac{w_{\mathrm{an},\mathrm{in},\mathrm{vap}}{\dot{m}}_{\mathrm{an},\mathrm{in}}+w_{\mathrm{an},\mathrm{cm},\mathrm{vap}}{\dot{m}}_{\mathrm{an},\mathrm{reci}}}{{\dot{m}}_{\mathrm{an},\mathrm{cm},\mathrm{sm}}},\hfill \\ \hfill {\dot{m}}_{\mathrm{an},\mathrm{s},\mathrm{vap}}& =-{\dot{m}}_{\mathrm{m},\mathrm{vap}}-{\dot{m}}_{\mathrm{an},\mathrm{phase}}.\hfill \end{array}\end{array}$$

(27)

Here, $w_{\mathrm{an},\mathrm{in},{\mathrm{H}}_2}$ and $w_{\mathrm{an},\mathrm{in},\mathrm{vap}}=\left(1-w_{\mathrm{an},\mathrm{in},{\mathrm{H}}_2}\right)$ denote the dry hydrogen and vapor mass fractions in the inlet flow, respectively. The supply manifold mass fractions $w_{\mathrm{an},\mathrm{sm},i}$ are the mass-weighted averages of the inlet and the additional recirculation flow. The fuel consumption due to the electrochemical reaction governs the mass balance (25).

Furthermore, no water is produced in the anode, different from the cathode, due to the FC reaction. Therefore, no approximated GDL properties are necessary, and hence, the vapor partial pressure in the lumped anode volume $p_{\mathrm{an},\mathrm{vap}}$ governs the phase change rate.

2.1.3. Membrane

The membrane is a static submodel except for the membrane water activity $a_{\mathrm{m}}$, which has dynamics to replicate the transient membrane wetting and drying. A common approach is to model the membrane water activity as the average of the cathode $a_{\mathrm{ca}}=p_{\mathrm{ca},\mathrm{vap}}/p_{\mathrm{sat}}$ and anode water activities $a_{\mathrm{an}}=p_{\mathrm{an},\mathrm{vap}}/p_{\mathrm{sat}}$ [28]. However, this work uses the water activity at the cathode GDL $a_{\mathrm{ca},\mathrm{GDL}}=p_{\mathrm{ca},\mathrm{GDL},\mathrm{vap}}/p_{\mathrm{sat}}$ for the reasons outlined above, and a simple first-order relation:

$${\dot{a}}_{\mathrm{m}}=\frac{1}{{\tau }_{\mathrm{m}}}\left(\frac{a_{\mathrm{ca},\mathrm{GDL}}+a_{\mathrm{an}}}{2}-a_{\mathrm{m}}\right)$$

(28)

describes the membrane water activity dynamics. Here, ${\tau }_{\mathrm{m}}$ is the characteristic time constant of the membrane, which is interpreted as the membrane water capacity. The polynomial presented in [29] describes the relationship between membrane water activity and membrane water content $\lambda$. The polynomial was determined at 80 ${}^{°}\mathrm{C}$, which is the nominal operating temperature in many cases:

$$\begin{array}{c}\hfill {\lambda }_j=\left\{\begin{array}{cc}0.3+10.8a_j-16a_j^2+14.1a_j^3,\hfill & 0\le a_j\le 1\hfill \\ 9.2+3.8(a_j-1),\hfill & 1<a_j\le 3\hfill \end{array}\right.\mathrm{for}j\in \{(\mathrm{ca},\mathrm{GDL}),\mathrm{an},\mathrm{m}\}\end{array}$$

(29)

Here, ${\lambda }_{\mathrm{ca},\mathrm{GDL}}$ and ${\lambda }_{\mathrm{an}}$ are understood as the membrane water uptake at the cathode GDL and anode side, respectively. In [30], it was observed that the membrane water content went up to 16.8 at 80 ${}^{°}\mathrm{C}$ in liquid water immersed membranes. For modeling purposes, the water content linearly increases from 9.2 to 16.8 for a water activity value from 1–3. The switching behavior is obtainable by using the differentiable switching function, as shown above.

Related to the membrane water uptake is the ohmic resistance of the membrane $R_{\mathrm{m}}$. The former affects the membrane’s ionic conductivity [30]:

$${\sigma }_{\mathrm{m}}=(0.005139{\lambda }_{\mathrm{m}}-0.00326)exp\left[1268\left(\frac{1}{303}-\frac{1}{T}\right)\right]{10}^2,$$

(30)

which subsequently yields the ohmic resistance:

$$R_{\mathrm{m}}=\frac{{\delta }_{\mathrm{m}}}{{\sigma }_{\mathrm{m}}{A}_{\mathrm{cell}}}+R_{\mathrm{c}}.$$

(31)

Here, ${\delta }_{\mathrm{m}}$ denotes the membrane thickness and $R_{\mathrm{c}}$ the ohmic contact resistance. The mass flow ${\dot{m}}_{\mathrm{m},\mathrm{vap}}$ is also dependent on the membrane water content and combines the electro-osmotic drag and back-diffusion flow of vapor through the membrane. This phenomenon was described in [31], and some prerequisite quantities are necessary to determine the named flow. First, the membrane surface water concentrations for the cathode GDL $c_{\mathrm{ca},\mathrm{GDL}}={\lambda }_{\mathrm{ca},\mathrm{GDL}}{\rho }_{\mathrm{m},\mathrm{dry}}/M_{\mathrm{m},\mathrm{dry}}$ and anode $c_{\mathrm{an}}={\lambda }_{\mathrm{an}}{\rho }_{\mathrm{m},\mathrm{dry}}/M_{\mathrm{m},\mathrm{dry}}$ are needed. Here, ${\rho }_{\mathrm{m},\mathrm{dry}}$ denotes the dry membrane density and $M_{\mathrm{m},\mathrm{dry}}$ the equivalent weight of the dry membrane. Second, the electro-osmotic drag coefficient:

$$n_{\mathrm{d}}=0.0029{\lambda }_{\mathrm{m}}^2+0.05{\lambda }_{\mathrm{m}}-3.4·{10}^{-19}$$

(32)

describes the number of water molecules carried per proton, and the water diffusion coefficient:

$$D=1.25exp\left[2416\left(\frac{1}{303}-\frac{1}{T}\right)\right]{10}^{-10}$$

(33)

is required to model the diffusion due to the water concentration gradient. Finally, merging all the quantities yields the vapor flow from the anode to the cathode:

$${\dot{m}}_{\mathrm{m},\mathrm{vap}}=M_{\mathrm{vap}}{A}_{\mathrm{cell}}{n}_{\mathrm{cell}}\left(\frac{n_{\mathrm{d}}I}{A_{\mathrm{cell}}\mathcal{F}}-D\frac{c_{\mathrm{ca},\mathrm{GDL}}-c_{\mathrm{an}}}{{\delta }_{\mathrm{m}}}\right).$$

(34)

Besides the vapor flow, nitrogen also diffuses through the membrane, which was investigated in detail in [32]. The derived nitrogen permeance through the membrane is:

$$k_{\mathrm{m},{\mathrm{N}}_2}=\frac{M_{{\mathrm{N}}_2}{A}_{\mathrm{cell}}{n}_{\mathrm{cell}}}{{\delta }_{\mathrm{m}}}(0.0295+1.21f-1.93f^2)exp\left[\frac{E_{{\mathrm{N}}_2}}{\mathcal{R}}\left(\frac{1}{303}-\frac{1}{T}\right)\right]{10}^{-14},$$

(35)

where $E_{{\mathrm{N}}_2}$ is the activation energy of nitrogen, and the volume fraction of water in the membrane [33] is determinable by:

$$f=\frac{{\lambda }_{\mathrm{m}}{\overline{V}}_{\mathrm{vap}}}{{\overline{V}}_{\mathrm{m}}+{\lambda }_{\mathrm{m}}{\overline{V}}_{\mathrm{vap}}}.$$

(36)

Here, ${\overline{V}}_{\mathrm{vap}}$ denotes the molar volume of vapor and ${\overline{V}}_{\mathrm{m}}=M_{\mathrm{m},\mathrm{dry}}/{\rho }_{\mathrm{m},\mathrm{dry}}$ the molar volume of the membrane. Using the derived nitrogen permeance and the respective nitrogen partial pressures yields the nitrogen flow from the cathode to the anode:

$${\dot{m}}_{\mathrm{m},{\mathrm{N}}_2}=k_{\mathrm{m},{\mathrm{N}}_2}(p_{\mathrm{ca},{\mathrm{N}}_2}-p_{\mathrm{an},{\mathrm{N}}_2}).$$

(37)

2.1.4. Electrochemistry

The electrochemical submodel interconnects the current, internal thermodynamic states, and voltage. This work utilized the thermodynamically consistent electrochemical model from [21], which has reasonable extrapolation capabilities while only needing a handful of tuning parameters. Additionally, the explicitly defined limit currents are beneficial for the implementation of the liquid water flooding effects. The voltage per cell is defined by:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill U_{\mathrm{cell}}=& \frac{k_{\mathrm{B}}T}{e{Z}_{\mathrm{ca}}}ln\left({\left(C_{\mathrm{ca},\mathrm{vap}}\left(1+\frac{2I}{I_{\mathrm{ca},\mathrm{lm}}}\right)\right)}^{-2}\left(C_{\mathrm{ca},{\mathrm{O}}_2}\left(1-\frac{I}{I_{\mathrm{ca},\mathrm{lm}}}\right)\right)\right)-\frac{\Delta g_{\mathrm{ca},\mathrm{ref}}}{e{Z}_{\mathrm{ca}}}+\hfill \\ \hfill & -\frac{k_{\mathrm{B}}T}{e{Z}_{\mathrm{an}}}ln\left({\left(C_{\mathrm{an},{\mathrm{H}}_2}\left(1-\frac{I}{I_{\mathrm{an},\mathrm{lm}}}\right)\right)}^2\right)+\frac{\Delta g_{\mathrm{an},\mathrm{ref}}}{e{Z}_{\mathrm{an}}}+\hfill \\ \hfill & +\frac{\left(T-T_{\mathrm{ref}}\right)\Delta s_{\mathrm{ca}}}{e{Z}_{\mathrm{ca}}}-\frac{\left(T-T_{\mathrm{ref}}\right)\Delta s_{\mathrm{an}}}{e{Z}_{\mathrm{an}}}-R_{\mathrm{m}}I+\hfill \\ \hfill & -\frac{k_{\mathrm{B}}T}{e{Z}_{\mathrm{ca}}}\mathrm{arcsinh}\left(\frac{I}{2I_{\mathrm{ca},\mathrm{ie}}}{\left(C_{\mathrm{ca},\mathrm{vap}}\left(1+\frac{2I}{I_{\mathrm{ca},\mathrm{lm}}}\right)\right)}^{-1}{\left(C_{\mathrm{ca},{\mathrm{O}}_2}\left(1-\frac{I}{I_{\mathrm{ca},\mathrm{lm}}}\right)\right)}^{-0.5}\right)+\hfill \\ \hfill & -\frac{k_{\mathrm{B}}T}{e{Z}_{\mathrm{an}}}\mathrm{arcsinh}\left(\frac{I}{2I_{\mathrm{an},\mathrm{ie}}}{\left(C_{\mathrm{a},{\mathrm{H}}_2}\left(1-\frac{I}{I_{\mathrm{an},\mathrm{lm}}}\right)\right)}^{-1}\right).\hfill \end{array}\end{array}$$

(38)

In the electrochemical model, $k_{\mathrm{B}}$ denotes the Boltzmann constant, e the elementary charge, $Z_n$ for $n\in \{\mathrm{ca},\mathrm{an}\}$ the number of electrons transferred in the electrochemical reaction on the cathode and anode side, respectively, $\Delta g_{n,\mathrm{ref}}$ the specific Gibbs free energy at the reference temperature $T_{\mathrm{ref}}$, and $\Delta s$ the specific entropy. Furthermore, the unitless concentrations of the gaseous species:

$$\begin{array}{c}\hfill C_{n,i}=\frac{p_{n,i}}{p_{\mathrm{atm}}}\mathrm{for}\left\{\begin{array}{cc}i\in \{{\mathrm{O}}_2,\mathrm{vap}\},\hfill & n=\mathrm{ca}\hfill \\ i={\mathrm{H}}_2,\hfill & n=\mathrm{an}\hfill \end{array}\right.\end{array}$$

(39)

are obtainable by normalizing the respective partial pressures to the atmospheric pressure. The intrinsic exchange current is determinable by:

$$I_{n,\mathrm{ie}}=A_{\mathrm{cell}}exp\left(\frac{0.5\Delta s_n(T-T_{\mathrm{ref}})}{k_{\mathrm{B}}T}\right)K_n,$$

(40)

where $K_n$ is the intrinsic exchange current parameter. The limit current is evaluated with:

$$I_{n,\mathrm{lm}}=Z_n\mathcal{F}{C}_{n,i}C{D}_n{(1-s_n)}^{1.5}\mathrm{for}\left\{\begin{array}{c}i={\mathrm{O}}_2,n=\mathrm{ca}\hfill \\ i={\mathrm{H}}_2,n=\mathrm{an}\hfill \end{array}\right.$$

(41)

where $C{D}_n$ denotes the combined diffusivity parameter. For more insight into this model, see [21,34]. Note that the term ${(1-s_n)}^{1.5}$ with the liquid water saturation $s_n$ is the additionally implemented Bruggeman relationship based on the EMT [35,36,37], which takes the flooding effects into account. Under the assumption that every cell is identical, multiplying the voltage per cell with the total number of cells yields the stack voltage $U=U_{\mathrm{cell}}{n}_{\mathrm{cell}}$.

2.1.5. Overview

The control-oriented model described above is summarized into the nonlinear state-space model:

$$\begin{array}{cc}\hfill \dot{\mathbf{x}}& =\mathbf{f}(\mathbf{x},\mathbf{u},\mathbf{\Theta }),\hfill \end{array}$$

(42)

$$\begin{array}{cc}\hfill \mathbf{y}& =\mathbf{g}(\mathbf{x},\mathbf{u},\mathbf{\Theta }),\hfill \end{array}$$

(43)

where the vectors are structured as follows:

$$\begin{array}{cc}\hfill \mathbf{x}& ={[m_{\mathrm{ca},{\mathrm{O}}_2},m_{\mathrm{ca},{\mathrm{N}}_2},m_{\mathrm{ca},\mathrm{vap}},m_{\mathrm{ca},\mathrm{liq}},m_{\mathrm{an},{\mathrm{H}}_2},m_{\mathrm{an},{\mathrm{N}}_2},m_{\mathrm{an},\mathrm{vap}},m_{\mathrm{an},\mathrm{liq}},a_{\mathrm{m}}]}^{\mathrm{T}},\hfill \end{array}$$

(44)

$$\begin{array}{cc}\hfill \mathbf{u}& ={[{\dot{m}}_{\mathrm{ca},\mathrm{in}},{\phi }_{\mathrm{ca},\mathrm{in}},{\alpha }_{\mathrm{ca}},p_{\mathrm{an},\mathrm{sm}},{\phi }_{\mathrm{an},\mathrm{in}},{\alpha }_{\mathrm{an}},P_{\mathrm{an},\mathrm{reci}},p_{\mathrm{atm}},I,T]}^{\mathrm{T}},\hfill \end{array}$$

(45)

$$\begin{array}{cc}\hfill \mathbf{y}& ={[U,p_{\mathrm{ca},\mathrm{sm}},p_{\mathrm{ca},\mathrm{em}},{\dot{m}}_{\mathrm{an},\mathrm{in}},p_{\mathrm{an},\mathrm{em}}]}^{\mathrm{T}}.\hfill \end{array}$$

(46)

In Equations (42) and (43), $\mathbf{x}\in {\mathbb{R}}^9$ denotes the state vector, $\mathbf{u}\in {\mathbb{R}}^{10}$ the input vector, $\mathbf{y}\in {\mathbb{R}}^5$ the output vector, $\mathsf{\Theta }\in {\mathbb{R}}^{n_{\mathsf{\Theta }}}$ the vector containing the tunable parameters ${\mathsf{\Theta }}_l$ for $l\in \{1,2,\cdots ,n_{\mathsf{\Theta }}\}$, $n_{\mathsf{\Theta }}$ the number of parameters, $\mathbf{f}$ the system function, and $\mathbf{g}$ the output function [38].

2.2. Experimental Setup

A PEMFC system test bench delivered the measurement data for model parameterization and validation. The test bench consisted mainly of a 30 kW PEMFC stack, a hydrogen supply system, an air-supply system, the cooling circuits, as well as the measurement and control system. The experiments consisted of load point changes of the FC stack through a dynamic DC/AC inverter (battery simulator). The battery simulator was capable of controlling either the current or the voltage level. The latter was used in the given experiment. Furthermore, the battery simulator supplied the electric power generated by the FC stack during operation into the electric grid, and an additional power supply system fed the balance of plant components with energy. A more detailed description of the test bench and the experimental conditions is available in [18].

2.3. Parametrization

The optimized parameters of the model were the result of the following optimization problem:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {\mathsf{\Theta }}_{\mathrm{opt}}=\underset{\mathsf{\Theta }}{argmin}J\left(\mathsf{\Theta }\right)\\ \hfill \mathrm{with}\mathrm{respect}\mathrm{to}\\ \hfill {\mathsf{\Theta }}_{l,\min }\le {\mathsf{\Theta }}_l\le {\mathsf{\Theta }}_{l,\max }.\end{array}\end{array}$$

(47)

The bounds of the parameters, ${\mathsf{\Theta }}_{l,\min }$ and ${\mathsf{\Theta }}_{l,\max }$, were determined from physical considerations and experience. Solving the state-space models (42) and (43) with a given input signal $\mathbf{u}\left(t\right)$ and a parameter set Θ in continuous time t yielded the simulated output signal $\mathbf{y}(t,\mathsf{\Theta })$, which resulted in the sampled one $\mathbf{y}(t_k,\mathsf{\Theta })$ by sampling it at instants $t_k$ for $k\in \{1,2,\cdots ,n_k\}$. The sampled signal was necessary for the parametrization, and $n_k$ is the number of sampling instants. The objective function J considers the weighted squared errors between the measured ${\mathbf{y}}^{*}\left(t_k\right)$ and simulated output signals $\mathbf{y}(t_k,\mathsf{\Theta })$ [18,39]:

$$\begin{array}{c}\hfill J\left(\mathsf{\Theta }\right)=\sum _{k=0}^{n_k}{\left(\mathbf{y}(t_k,\mathsf{\Theta })-{\mathbf{y}}^{*}\left(t_k\right)\right)}^{\mathrm{T}}{\mathbf{Q}}_{\mathbf{y}}\left(\mathbf{y}(t_k,\mathsf{\Theta })-{\mathbf{y}}^{*}\left(t_k\right)\right)\end{array}$$

(48)

Here, ${\mathbf{Q}}_{\mathbf{y}}\in {\mathbb{R}}^{5\times 5}$ is the output weighting matrix, which allows the weighting of each output component and considering the different component magnitudes. This work used MATLAB R2019b to conduct the simulation and optimization. Euler’s method [40] was used to solve the ordinary differential equation (ODE) system (42), and the initial condition for the ODE system was determined by assuming steady-state conditions at the first sample. Last but not least, the optimization was conducted with the genetic algorithm combined with the fmincon optimizer [41].

3. Results and Discussion

This section presents the results obtained with the parametrized model derived above, including a detailed discussion of the outcomes. Figure 3 shows the simulated outputs compared to the measurement data with the corresponding $R^2$ values. The figure also depicts measured inputs for reference: the current I, the incoming cathode mass flow ${\dot{m}}_{\mathrm{ca},\mathrm{in}}$, the FC temperature T, the anode supply manifold pressure $p_{\mathrm{an},\mathrm{sm}}$, and the anode recirculation pump power $P_{\mathrm{an},\mathrm{reci}}$. The model achieved an $R^2$ value of 98.3% between the simulated stack voltage and the measured counterpart, 99.9% for the cathode supply manifold pressure, 99.2% for the cathode exit manifold pressure, 96.9% for the incoming anode mass flow, and 72.0% for the anode exit manifold pressure. An average $R^2$ value of 93.3% was achieved by the model, which provided the required accuracy for control applications and validating the proposed modeling approaches in this work. Especially remarkable was the significantly lower agreement of the anode exit manifold pressure $p_{\mathrm{an},\mathrm{em}}$ in Figure 3e compared to the others. The reason was that this work approximated the unmeasured recirculation volume flow by assuming that the flow is only proportional to the recirculation pump power $P_{\mathrm{an},\mathrm{reci}}$. Strictly speaking, the recirculation flow is also inversely proportional to the pressure difference over the pump $(p_{\mathrm{an},\mathrm{sm}}-p_{\mathrm{an},\mathrm{em}})$. However, by including the pressure difference in the expression of the recirculation flow, ${\dot{V}}_{\mathrm{an},\mathrm{reci}}=k_{\mathrm{an},\mathrm{reci}}{P}_{\mathrm{an},\mathrm{reci}}/(p_{\mathrm{an},\mathrm{sm}}-p_{\mathrm{an},\mathrm{em}})$, the anode exit manifold pressure $p_{\mathrm{an},\mathrm{em}}$ is no longer explicitly expressible with the given mass balance (23). Therefore, minor deviations of the simulated signal are accepted to obtain a closed-form expression for $p_{\mathrm{an},\mathrm{em}}$. If the recirculation flow were additionally measured and implemented as an input to the model, the corresponding $R^2$ value would increase.

Figure 4 depicts the simulated internal FC model states, allowing an analysis of the species composition, which is crucial for precise control and avoiding the operating conditions leading to severe degradation. The figure illustrates the simulated gaseous species in the cathode and anode in molar fractions and the liquid water in terms of saturation. Generally speaking, the displayed internal states were considered plausible and match the expected values from experience and expert knowledge. In Figure 4a, the molar fractions of oxygen and nitrogen are lower than in dry air because the cathode gas is humid, nitrogen diffuses to the anode, and oxygen is consumed. The oxygen trajectory dropped to a lower level at around 200 to 1700 $\mathrm{s}$ due to the load application. In Figure 4b, the effects of purging in the anode are well visible, indicated by the sharp drops and rises, respectively. The fraction of vapor in the anode rose with increasing FC load and vice versa. Interestingly, there was barely any liquid water in the anode for the given experiment, indicated by the anode liquid water saturation in Figure 4c.

Figure 5 pictures the simulated condensation and evaporation behavior of the FC. On the one hand, it shows the respective vapor partial pressures versus the saturation pressure, and on the other hand, it depicts the phase change rates in the lumped volumes. In the cathode GDL, condensation always occurs because the vapor partial pressure was above the saturation pressure all the time, shown in Figure 5a. This behavior was to be expected due to the continuously high FC loads and, thus, high water generation. On the anode side, the vapor partial pressure was most of the time below the saturation pressure. Therefore, mainly evaporation occurred, visible in Figure 4c by the decreasing anode liquid water saturation. The magnitude of the latter was minimal because there was barely any liquid water in the anode. According to the simulation, condensation in the anode happened at only one sample at the end of the experiment, indicated by the red vertical line in Figure 5b. Phase change mainly happened in the cathode GDL, where the corresponding phase change rate had a three-times bigger magnitude than the anode one.

Figure 6 presents the simulated droplet removal mechanisms in the cathode. It shows the forces acting on a droplet, the droplet removal rate, and the reduced liquid water saturation, which was necessary to determine the depicted average droplet radius. Figure 6a shows the individual forces acting on a droplet. As seen in Figure 6b, the droplets started to form at around 800 $\mathrm{s}$ when the reduced liquid water saturation became nonzero. At that time, the adhesion force $F_{\mathrm{ca},\mathrm{ad}}$ was much more significant than the pushing force $F_{\mathrm{ca},\mathrm{push}}$, leading to no droplet removal. With a rising droplet radius, the pushing force, dominantly the shear force $F_{\mathrm{ca},\mathrm{sh}}$, increased as well. In this case, the pressure drop force $F_{\mathrm{ca},\mathrm{pd}}$ was tiny, but it should not be disregarded, especially at higher volume flows. The gravitational force $F_{\mathrm{ca},\mathrm{g}}$ is almost not visible because it is in principle congruent with the zero-line, confirming the previously made assumption that its impact on the liquid water droplet removal is almost negligible. When the pushing force exceeded the adhesion force (e.g., shortly after 1300 $\mathrm{s}$), droplet removal occurred, visible in Figure 6c. A little after 1400 $\mathrm{s}$, there was a significant peak in the pushing force. The reason was that the current decreased at that time, which led to fewer droplet injection points according to our modeling assumptions. The amount of liquid water barely changed simultaneously, and the given combination led to bigger average liquid water droplets. The rapid growth of the droplet size increased the pushing force and subsequently enforced droplet removal. The droplet removal rate looked unusual due to the many thin spikes. One could assume that this was a numerical issue, but computational fluid dynamic simulations [42] and experimental results [43] showed that liquid water leaves the FC in waves, confirming our simulations. The reduced liquid water saturation, determining the droplet size and illustrated in Figure 6b, was less than the liquid water saturation shown in Figure 4c. The reason was that water first needs to accumulate in the GDL until the individual droplets start to connect into streams. This transitioning was modeled with the immobile saturation threshold, which, when exceeded, enabled the flow of accumulated water into the channels where it started to form droplets. Because of this reasoning, there was no droplet removal in the anode for the given experiment because the liquid water saturation there was always below the immobile water saturation.

Figure 7 compares the simulated membrane water contents and the resulting ohmic membrane resistances of the FC, evaluated with the polynomials determined by Springer et al. [30] and Hinatsu et al. [29]. The membrane water activity was over one, which explains why the trajectories of the membrane water contents shown in Figure 7a are above the respective unsaturated regions (the unsaturated region ended at 14 for Springer et al. and 9.2 for Hinatsu et al.). The water content obtained with Hinatsu et al. was on average one-third smaller than the one obtained with Springer et al., simply because the named authors derived the relationships at different temperatures. The latter determined the relationships at 30 ${}^{°}\mathrm{C}$ and the former at 80 ${}^{°}\mathrm{C}$, which is the nominal FC operating temperature in many cases. The different water contents subsequently affected the ohmic membrane resistances, pictured in Figure 7b. The water content derived by Hinatsu et al. is smaller than the one derived by Springer et al., which leads to a 50 bigger ohmic membrane resistance on average. Of course, this circumstance affected the simulated voltage and power output of the FC.

The simulated effects of flooding on the electrochemical reaction considered by the EMT are visible in Figure 8. The so-called Bruggeman relationship [35] scaled with the bulk diffusivity yields the effective counterpart. Figure 8a pictures this scaling term for the cathode and anode. The effective diffusivity of the cathode dropped one-third over time, while the one for the anode essentially remained constant. The reason was that liquid water accumulated in the cathode during operation, and simultaneously, there was almost no liquid water in the anode. Therefore, if relatively dry operating conditions dominate, the anode liquid water state could be removed to reduce the model complexity [2]. Figure 8b illustrates the deviation of the voltage due to the EMT, and the effects of flooding were minimal because the shown measurements resulted from a voltage-controlled experiment. Flooding effects would be more prominent in experiments explicitly provoking them.

The key message of this section is that the proposed model delivered plausible water states compared to existing models, which is invaluable for diagnosis, simulation, and control. A typical property for control-oriented models is that they have no spatial distribution. Therefore, the model relies on various kinds of physical approximations to efficiently replicate the spatial distribution, and it tries to mimic the delay between the flooded GDL and channel with the immobile saturation. The capability of replicating flooding effects is beneficial for predictive control methodologies in order to prevent it. The proposed model yields the prerequisites to derive advanced control strategies to improve water management and mitigate degradation phenomena correlated with the water transients of PEMFCs.

4. Conclusions

This work proposed a control-oriented PEMFC stack model focusing on physically motivated water modeling. For the first time and in contrast to available models, the latter covers phase change, liquid water removal, membrane water uptake, and water flooding effects on the electrochemical reaction in a control-oriented stack model. The water phase change is modeled via an adapted Hertz–Knudsen equation, and liquid water removal is governed by a force balance over an average droplet. The membrane water uptake is obtained with a function determined at the nominal FC operating temperature, and liquid water effects on the electrochemical reaction are replicated by employing the EMT. Physically modeling the named effects enables new insights into the transient water effects in the FC, which were thoroughly analyzed and discussed in this work. The model achieved an average $R^2$ value of 93.3% between the model output and experimental data, which provided the required accuracy for control applications. Furthermore, the validation with transient measurement data confirmed not only the plausibility of the modeling basis with the convincing simulation results and good model agreement, but also the possibility of adequately simulating the internal states of the FC. On the one hand, the model’s novelties enable a physically based replication of water phase change and liquid water removal. On the other hand, a more accurate membrane water content and the flooding capability allow a more precise simulation of the electrochemical reaction. In summary, the model yields invaluable insights into the FC water mechanisms, allowing their subsequent use in the development processes of advanced diagnostic, monitoring, and control solutions, aiming at combined performance and service life optimizations.

Subsequent research topics are validating the internal states with in situ measurements and additional improvements of the water modeling. On the one hand, the derivation of predictive control strategies to mitigate degradation phenomena and, on the other hand, the optimization of water management are also promising research topics.