Zeolite NaY-Copper Composites Produced by Sintering Processes for Adsorption Heat Transformation—Technology, Structure and Performance
Abstract
:1. Introduction
- short diffusion and thermal transport lengths in the adsorption material
- low mass transfer resistance in the macroporous structure
- low thermal contact resistance between adsorbent and heat exchanger
- high thermal conductivity and low thermal capacity of the heat exchanger
- low amount of heat transfer fluid in the hydraulic cycle, since the dead thermal mass of the heat transfer fluid must be considered [33].
- How good is the performance of NaY-copper composites in terms of overall sorption dynamics in comparison to a NaY loose grains configuration?
- Is heat or mass transfer dominating the overall sorption dynamics of NaY-copper composites?
- How big is the impact of the additional copper in NaY-copper composites on the overall thermal mass of an adsorption heat exchanger compared to a loose grain configuration?
2. Materials and Methods
2.1. Manufacturing Process
- we55: 10 g milled zeolite of the fraction 400–750 µm was moistened with 2.5 g water. Afterwards, 3.8 g SILIKOPHEN P 80/X (Evonik, Essen, Germany) binder was added to the zeolite bulk and stirred manually. Then 30 g technically pure Cu-fibers (STAX micro F08, Deutsches Metallfaserwerk, Neidenstein, Germany) were added and the mixture was stirred slowly. The mixture was filled into a cylindrical die with 50 mm diameter and compacted with a press (MATRA, Matra-Werke GmbH, Hainburg, Germany) with a force of 100 kN. The sample was dried, first at room temperature, and afterwards at 420 °C. Sintering was done for 3 h at 600 °C in hydrogen atmosphere in a sintering furnace (ThermalTechnology LLC, Santa Rosa, CA, USA).
- we95: in comparison to sample we55, 10 g milled zeolite of the fraction 63–125 µm and Cu powder (25 g, Schlenk Offset 6127) were used for the mixture. The compaction was done with part of the mixture, again in a 50 mm die. Because of the different compaction behavior of this mixture the compaction force was reduced to 20 kN. The sample was then treated in the same way as sample we55.
2.2. Characterization Methods
2.3. Evaluation of Heat and Mass Transfer Resistances
3. Results
3.1. Evaluation of Thermophysical Quantities
- The overall thermal mass is relevant for the interpretation of the inert-LTJ experiments. The higher the thermal mass, the longer the equilibration of the temperature takes if the samples have the same thermal resistance.
- The adsorbent mass per composite volume is an important quantity for the heat exchanger design: the higher this figure, the more compact the heat exchanger will be. This is the basis for a high power density.
- The specific thermal mass (STM) per adsorbent mass according to Gluesenkamp et al., in Equation (11) is an indicator for the efficiency that can be achieved if the structure is applied in an adsorption heat exchanger [33]. The lower this quantity is, the more efficient a simple adsorption cycle without heat recovery will be as less heat is required to change the adsorption heat exchanger temperature between adsorption and desorption.
3.2. Heat Transfer Properties
3.3. Sorption Equilibrium Data
3.4. Evaluation of Sorption Dynamics
- desorption of we55 is only heat transfer limited
- adsorption and desorption of we95 is only mass transfer limited
- adsorption of we55 is both heat- and mass transfer limited.
- The mass transfer in the adsorbent metal composite happens on a macro pore level. Here, a characteristic flow path length and the mean diameter of the macro pores have an impact on the flow of water vapor through the structure [62,63]. The characteristic flow path length is in the range of the sample height: here 3.5 mm for we95 and 5.3 mm for we55. A mean macro pore diameter was not measured so far but we can assume that the macro pores of sample we55 are larger than the macro pores of sample we95 from the microscopic imaging in Figure 1. Since the macro pore mass transfer processes (viscous flow and Knudsen diffusion) strongly depend on the absolute pressure [43,62,64], this could be an explanation for the difference between adsorption (low pressure, high mass transfer resistance) and desorption (high pressure, low mass transfer resistance).
- The vapor transport within the adsorbent particles will happen on macro- or mesopore level, here the characteristic path length is 30–70 µm for we95 and around 200 µm for we55. The mean macro- or mesopore diameter should be the same for both samples, since we use different sieve fractions from the same material. From measurements of the loose grain configuration as carried out by Girnik and Aristov [65,66] with different granule diameters, we would expect a higher resistance for sample we55 if the vapor transport within the adsorbent particles played a role. Instead, we observed an inverse behavior: sample we95 with small granule diameter is much slower than sample we55 with larger granules. Thus, we can assume that the vapor transport within the adsorbent particles is not important for the overall sorption dynamics.
- The mass transfer on the micro pore level of the adsorbent crystals in the particles is likely dominated by the diffusion of the adsorbate within the adsorbent crystals. Here, the mass transfer resistance should be the same for both samples, since we use different sieve fractions from the same material with the same properties on the micro pore level. Thus, the mass transfer on the micro pore level is also not important for the overall sorption dynamics.
3.5. Comparison with Other Adsorbent Metal Structures
3.6. Heat Exchanger Design
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature and Indices
| Symbol | Unit | Description |
| A | J/kg | Adsorption potential |
| T | K | Temperature |
| p | Pa | Pressure |
| X | g/g | Loading |
| W | Heat flux | |
| J/K | Effective heat capacity | |
| K/W | Heat or mass transfer resistance | |
| J/(kg·K) | Specific gas constant | |
| J/kg | Adsorption enthalpy | |
| kg | Adsorbent mass | |
| J/kg | Evaporation/condensation enthalpy | |
| J/(kg·K) | Specific heat capacity | |
| K/W | Heat and mass transfer impedance (* indicates capacitive effects) | |
| K/W | Time averaged heat or mass transfer resistance | |
| cm2K/W | Area scaled time averaged heat or mass transfer resistance | |
| J/(kg·K) | Specific thermal mass | |
| W/(m2·K) | Heat transfer coefficient | |
| W/(m·K) | Thermal conductivity |
| Index | Description |
| init | Initial value |
| end | End value |
| sat | Saturation |
| N2 | Nitrogen |
| eqi | Equilibrium |
| cmp | Composite |
| vap | Vapour |
| s | Sorptive term |
| MT | Mass transfer |
| HT | Heat transfer |
| Capacitive term | |
| cmp | Composite |
| car | Carrier plate |
| adb | Adsorbate |
| l | Liquid |
| rel | Relative |
| tot | Total |
| eff | Effective |
| mt | Metal |
References
- Wienen, J.; Neubert, M.; Lang, R.; Tiemeier, H. Results from field trial with gas heat pump Zeotherm by Vaillant. In Thermally Driven Heat Pumps for Heating and Cooling; Kühn, A., Ed.; Universitätsverlag der TU: Berlin, Germany, 2013. [Google Scholar]
- Núñez, T.; Mittelbach, W.; Henning, H.-M. Development of an adsorption chiller and heat pump for domestic heating and air-conditioning applications. Appl. Therm. Eng. 2007, 27, 2205–2212. [Google Scholar] [CrossRef]
- Schicktanz, M.; Nuñez, T. Modelling of an adsorption chiller for dynamic system simulation. Int. J. Refrig. 2009, 32, 588–595. [Google Scholar] [CrossRef]
- Meunier, F. Adsorption heat powered heat pumps. Appl. Therm. Eng. 2013, 61, 830–836. [Google Scholar] [CrossRef]
- Henninger, S.; Schmidt, F.; Henning, H.-M. Water adsorption characteristics of novel materials for heat transformation applications. Appl. Therm. Eng. 2010, 30, 1692–1702. [Google Scholar] [CrossRef]
- Henninger, S.K.; Ernst, S.-J.; Gordeeva, L.G.; Bendix, P.; Fröhlich, D.; Grekova, A.D.; Bonaccorsi, L.; Aristov, Y.; Jaenchen, J. New materials for adsorption heat transformation and storage. Renew. Energy 2017, 110, 59–68. [Google Scholar] [CrossRef]
- Henninger, S.K.; Jeremias, F.; Kummer, H.; Schossig, P.; Henning, H.-M. Novel Sorption Materials for Solar Heating and Cooling. Energy Procedia 2012, 30, 279–288. [Google Scholar] [CrossRef]
- Volmer, R.; Eckert, J.; Füldner, G.; Schnabel, L. Evaporator development for adsorption heat transformation devices–Influencing factors on non-stationary evaporation with tube-fin heat exchangers at sub-atmospheric pressure. Renew. Energy 2017, 110, 141–153. [Google Scholar] [CrossRef]
- Lanzerath, F.; Seiler, J.; Erdogan, M.; Schreiber, H.; Steinhilber, M.; Bardow, A. The impact of filling level resolved: Capillary-assisted evaporation of water for adsorption heat pumps. Appl. Therm. Eng. 2016, 102, 513–519. [Google Scholar] [CrossRef] [Green Version]
- Schnabel, L.; Füldner, G.; Velte, A.; Laurenz, E.; Bendix, P.; Kummer, H.; Wittstadt, U. Innovative Adsorbent Heat Exchangers: Design and Evaluation. In Innovative Heat Exchangers; Bart, H.-J., Scholl, S., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 363–394. [Google Scholar]
- Caprì, A.; Frazzica, A.; Calabrese, L. Recent Developments in Coating Technologies for Adsorption Heat Pumps: A Review. Coatings 2020, 10, 855. [Google Scholar] [CrossRef]
- Henninger, S.; Munz, G.; Ratzsch, K.-F.; Schossig, P. Cycle stability of sorption materials and composites for the use in heat pumps and cooling machines. Renew. Energy 2011, 36, 3043–3049. [Google Scholar] [CrossRef]
- Wang, R.; Xia, Z.; Wang, L.; Lu, Z.; Li, S.; Li, T.; Wu, J.; He, S. Heat transfer design in adsorption refrigeration systems for efficient use of low-grade thermal energy. Energy 2011, 36, 5425–5439. [Google Scholar] [CrossRef]
- Sharafian, A.; Bahrami, M. Assessment of adsorber bed designs in waste-heat driven adsorption cooling systems for vehicle air conditioning and refrigeration. Renew. Sustain. Energy Rev. 2014, 30, 440–451. [Google Scholar] [CrossRef]
- Riffel, D.B.; Wittstadt, U.; Schmidt, F.P.; Núñez, T.; Belo, F.A.; Leite, A.P.; Ziegler, F. Transient modeling of an adsorber using finned-tube heat exchanger. Int. J. Heat Mass Transf. 2010, 53, 1473–1482. [Google Scholar] [CrossRef]
- Kowsari, M.M.; Niazmand, H.; Tokarev, M.M. Bed configuration effects on the finned flat-tube adsorption heat exchanger performance: Numerical modeling and experimental validation. Appl. Energy 2018, 213, 540–554. [Google Scholar] [CrossRef]
- Demir, H.; Mobedi, M.; Ülkü, S. The use of metal piece additives to enhance heat transfer rate through an unconsolidated adsorbent bed. Int. J. Refrig. 2010, 33, 714–720. [Google Scholar] [CrossRef] [Green Version]
- Rezk, A.; Al-Dadah, R.; Mahmoud, S.; Elsayed, A. Effects of contact resistance and metal additives in finned-tube adsorbent beds on the performance of silica gel/water adsorption chiller. Appl. Therm. Eng. 2013, 53, 278–284. [Google Scholar] [CrossRef]
- Askalany, A.A.; Henninger, S.K.; Ghazy, M.; Saha, B.B. Effect of improving thermal conductivity of the adsorbent on performance of adsorption cooling system. Appl. Therm. Eng. 2017, 110, 695–702. [Google Scholar] [CrossRef]
- Kulakowska, A.; Pajdak, A.; Krzywanski, J.; Grabowska, K.; Zylka, A.; Sosnowski, M.; Wesolowska, M.; Sztekler, K.; Nowak, W. Effect of Metal and Carbon Nanotube Additives on the Thermal Diffusivity of a Silica Gel-Based Adsorption Bed. Energies 2020, 13, 1391. [Google Scholar] [CrossRef] [Green Version]
- Eun, T.-H.; Song, H.-K.; Han, J.H.; Lee, K.-H.; Kim, J.-N. Enhancement of heat and mass transfer in silica-expanded graphite composite blocks for adsorption heat pumps. Int. J. Refrig. 2000, 23, 64–73. [Google Scholar] [CrossRef]
- Pino, L.; Aristov, Y.; Cacciola, G.; Restuccia, G. Composite materials based on zeolite 4A for adsorption heat pumps. Adsorption 1997, 3, 33–40. [Google Scholar] [CrossRef]
- Ammann, J.; Ruch, P.; Michel, B.; Studart, A.R. Quantification of heat and mass transport limitations in adsorption heat exchangers: Application to the silica gel/water working pair. Int. J. Heat Mass Transf. 2018, 123, 331–341. [Google Scholar] [CrossRef]
- Bendix, P.; Füldner, G.; Möllers, M.; Kummer, H.; Schnabel, L.; Henninger, S.; Henning, H.-M. Optimization of power density and metal-to-adsorbent weight ratio in coated adsorbers for adsorptive heat transformation applications. Appl. Therm. Eng. 2017, 124, 83–90. [Google Scholar] [CrossRef]
- Freni, A.; Bonaccorsi, L.; Calabrese, L.; Caprì, A.; Frazzica, A.; Sapienza, A. SAPO-34 coated adsorbent heat exchanger for adsorption chillers. Appl. Therm. Eng. 2015, 82, 1–7. [Google Scholar] [CrossRef]
- Dawoud, B. Water vapor adsorption kinetics on small and full scale zeolite coated adsorbers; A comparison. Appl. Therm. Eng. 2013, 50, 1645–1651. [Google Scholar] [CrossRef]
- Ammann, J.; Michel, B.; Studart, A.R.; Ruch, P.W. Sorption rate enhancement in SAPO-34 zeolite by directed mass transfer channels. Int. J. Heat Mass Transf. 2019, 130, 25–32. [Google Scholar] [CrossRef]
- Ammann, J.; Michel, B.; Ruch, P.W. Characterization of transport limitations in SAPO-34 adsorbent coatings for adsorption heat pumps. Int. J. Heat Mass Transf. 2019, 129, 18–27. [Google Scholar] [CrossRef]
- Palomba, V.; Vasta, S.; Giacoppo, G.; Calabrese, L.; Gulli‘, G.; La Rosa, D.; Freni, A. Design of an Innovative Graphite Exchanger for Adsorption Heat Pumps and Chillers. Energy Procedia 2015, 81, 1030–1040. [Google Scholar] [CrossRef] [Green Version]
- Bauer, J.; Herrmann, R.; Mittelbach, W.; Schwieger, W. Zeolite/aluminum composite adsorbents for application in adsorption refrigeration. Int. J. Energy Res. 2009, 33, 1233–1249. [Google Scholar] [CrossRef]
- Wittstadt, U.; Füldner, G.; Andersen, O.; Herrmann, R.; Schmidt, F. A New Adsorbent Composite Material Based on Metal Fiber Technology and Its Application in Adsorption Heat Exchangers. Energies 2015, 8, 8431–8446. [Google Scholar] [CrossRef]
- Wittstadt, U.; Füldner, G.; Laurenz, E.; Warlo, A.; Große, A.; Herrmann, R.; Schnabel, L.; Mittelbach, W. A novel adsorption module with fiber heat exchangers: Performance analysis based on driving temperature differences. Renew. Energy 2017, 110, 154–161. [Google Scholar] [CrossRef]
- Gluesenkamp, K.R.; Frazzica, A.; Velte, A.; Metcalf, S.; Yang, Z.; Rouhani, M.; Blackman, C.; Qu, M.; Laurenz, E.; Rivero-Pacho, A.; et al. Experimentally Measured Thermal Masses of Adsorption Heat Exchangers. Energies 2020, 13, 1150. [Google Scholar] [CrossRef] [Green Version]
- Fink, M.; Andersen, O.; Seidel, T.; Schlott, A. Strongly Orthotropic Open Cell Porous Metal Structures for Heat Transfer Applications. Metals 2018, 8, 554. [Google Scholar] [CrossRef] [Green Version]
- Velte, A.; Herrmann, R.; Andersen, O.; Wittstadt, U.; Füldner, G.; Schnabel, L. Experimental Characterization of Aluminum Fibre/SAPO-34 Composites for Adsorption Heat Pump Applications. In Proceedings of the Heat Powered Cycles Conference, Heat Powered Cycles, Nottingham, UK, 28–30 June 2016. [Google Scholar]
- Busse, P.; Mittelbach, W.; Schmitz, G. Preparation of Sorption Memory Element, Useful as a Adsorber/Desorber Unit in Solid Sorption Heat Pump, Comprises Filling a Form with a Pouring of Sorbent Material; and Infiltrating into Gaps of Pouring, and Forming Open-Pourous Solid Body. DE102005001056 A1, published 01 July 2006. Available online: https://patents.google.com/patent/DE102005001056A1 (accessed on 2 December 2020).
- Berg, A.; Baumeister, J.; Rausch, G.; Busse, M.; Schnabel, L.; Bauer, J. Application of Aluminium Sponges in the Adsorption Refrigeration Engineering. In Proceedings of the International Conference on Porous Metals and Metallic Foams (MetFoam), Montreal, QC, Canada, 5–7 September 2007. [Google Scholar]
- Berg, A.; Weise, J.; Rausch, G.; Haesche, M.; Wostmann, F.J.; Busse, M. Druckgusstechnische Herstellung von offenporösen Aluminiumschäumen und Aluminium-Polymer-Hybridstrukturen. Giesserei 2005, 92, 24–27. [Google Scholar]
- Busse, M.; Wöstmann, F.-J.; Müller, T.; Melz, T.; Spies, P. Intelligente Gussteile–Einsatz adaptronischer Komponenten in Kombination mit Gussteilen. Giesserei 2006, 93, 48–53. [Google Scholar]
- Pille, C. In-process embedding of piezo sensors and RFID transponders into cast parts for autonomous manufacturing logistics. In Proceedings of the Smart Systems Integration 2010: 4th European Conference & Exhibition on Integration Issues of Miniaturized Systems–MEMS, MOEMS, ICs and Electronic Components, Como, Italy, 23–24 March 2010; Gessner, T., Ed.; VDE-Verl: Berlin, Germany, 2010. [Google Scholar]
- Henninger, S.K.; Hügenell, D.I.F.P.P.; Baumgartner, B.E.M.; Kummer, D.C.H.; Jeremias, F. “Stabisorp-2 (BWE12001): Untersuchung des Degradationsverhaltens von Sorptionsmaterialien und Verbundsystemen zur Wärmespeicherung und -transformation,” Fraunhofer Institut für Solare Energiesysteme (ISE). Available online: https://pudi.lubw.de/detailseite/-/publication/61779-STABISORP-2.pdf (accessed on 2 December 2020).
- Velte, A.; Füldner, G.; Laurenz, E.; Schnabel, L. Advanced Measurement and Simulation Procedure for the Identification of Heat and Mass Transfer Parameters in Dynamic Adsorption Experiments. Energies 2017, 10, 1130. [Google Scholar] [CrossRef] [Green Version]
- Füldner, G. Stofftransport und Adsorptionskinetik in porösen Adsorbenskompositen für Wärmetransformationsanwendungen. Ph.D. Thesis, University of Freiburg, Freiburg, Germany, 2015. [Google Scholar]
- Leinekugel-Le-Cocq, D.; Tayakout-Fayolle, M.; Le Gorrec, Y.; Jallut, C. A double linear driving force approximation for non-isothermal mass transfer modeling through bi-disperse adsorbents. Chem. Eng. Sci. 2007, 62, 4040–4053. [Google Scholar] [CrossRef]
- Wittstadt, U. Experimentelle und modellgestützte Charakterisierung von Adsorptionswärmeübertragern. Ph.D. Thesis, Fakultät III–Prozesswissenschaften, Technische Universität Berlin, Berlin, Germany, 2018. [Google Scholar]
- Freni, A.; Maggio, G.M.; Cipiti, F.; Aristov, Y.I. Simulation of water sorption dynamics in adsorption chillers: One, two and four layers of loose silica grains. Appl. Therm. Eng. 2012, 44, 69–77. [Google Scholar] [CrossRef]
- Graf, S.; Lanzerath, F.; Bardow, A. The IR-Large-Temperature-Jump method: Determining heat and mass transfer coefficients for adsorptive heat transformers. Appl. Therm. Eng. 2017, 126, 630–642. [Google Scholar] [CrossRef]
- Graf, S.; Lanzerath, F.; Sapienza, A.; Frazzica, A.; Freni, A.; Bardow, A. Prediction of SCP and COP for adsorption heat pumps and chillers by combining the large-temperature-jump method and dynamic modeling. Appl. Therm. Eng. 2016, 98, 900–909. [Google Scholar] [CrossRef]
- Lanzerath, F. Modellgestützte Entwicklung von Adsorptionswärmepumpen; Hochschulbibliothek der Rheinisch-Westfälischen Technischen Hochschule Aachen: Aachen, Germany, 2013. [Google Scholar]
- Lanzerath, F.; Bau, U.; Seiler, J.; Bardow, A. Optimal design of adsorption chillers based on a validated dynamic object-oriented model. Sci. Technol. Built Environ. 2015, 21, 248–257. [Google Scholar] [CrossRef] [Green Version]
- Velte, A. Experimentelle Arbeiten und Entwicklung von numerischen Modellen zur Analyse und Optimierung von erweiterten Adsorptionskreisläufen für die Wärmeversorgung von Gebäuden. Ph.D. Thesis, Technische Fakultät, Universität Freiburg, Freiburg, Germany, 2019. [Google Scholar]
- Wittstadt, U.; Laurenz, E.; Velte, A.; Füldner, G. Using Driving Temperature Difference Equivalents to Compare Heat and Mass Transport Limitations in Sorption Modules and Adsorption Heat Exchangers: Poster at the Sorption Friends Conference, 14–16.09.2015, Milazzo, Sicily, Italy. Available online: http://www.sorptionfriends.org/poster/ (accessed on 24 April 2017).
- Sapienza, A.; Velte, A.; Girnik, I.; Frazzica, A.; Füldner, G.; Schnabel, L.; Aristov, Y. “Water–Silica Siogel” working pair for adsorption chillers: Adsorption equilibrium and dynamics. Renew. Energy 2017, 110, 40–46. [Google Scholar] [CrossRef]
- Farrusseng, D.; Daniel, C.; Hamill, C.; Casaban, J.; Didriksen, T.; Blom, R.; Velte, A.; Fueldner, G.; Gantenbein, P.; Persdorf, P.; et al. Adsorber heat exchanger using Al-fumarate beads for heat-pump applications—A transport study. Faraday Discuss. 2020, 225, 384–402. [Google Scholar] [CrossRef] [PubMed]
- Aristov, Y.; Dawoud, B.; Glaznev, I.; Elyas, A. A new methodology of studying the dynamics of water sorption/desorption under real operating conditions of adsorption heat pumps: Experiment. Int. J. Heat Mass Transf. 2008, 51, 4966–4972. [Google Scholar] [CrossRef]
- Lenzen, D.; Bendix, P.; Reinsch, H.; Fröhlich, D.; Kummer, H.; Möllers, M.; Hügenell, P.P.C.; Gläser, R.; Henninger, S.; Stock, N. Scalable Green Synthesis and Full-Scale Test of the Metal-Organic Framework CAU-10-H for Use in Adsorption-Driven Chillers. Adv. Mater. 2018, 30. [Google Scholar] [CrossRef]
- Pinheiro, J.M.; Salústio, S.; Valente, A.A.; Silva, C.M. Adsorption heat pump optimization by experimental design and response surface methodology. Appl. Therm. Eng. 2018, 138, 849–860. [Google Scholar] [CrossRef]
- Qiu, L. Thermal Properties of Framework Materials: Selected Zeolites, Clathrates and an Organic Diol. Ph.D. Thesis, Dalhousie University, Halifax, NS, Canada, 2000. [Google Scholar]
- Green, D.W. Perry’s Chemical Engineers’ Handbook, 8th ed.; McGraw-Hill: New York, NY, USA, 2008. [Google Scholar]
- Schwamberger, V. Thermodynamische und numerische Untersuchung eines neuartigen Sorptionszyklus zur Anwendung in Adsorptionswärmepumpen und -kältemaschinen = Thermodynamic and Numerical Investigation of a Novel Sorption Cycle for Application in Adsorption Heat Pumps and Chillers. Ph.D. Thesis, Karlsruher Institut für Technologie (KIT), Karlsruhe, Germany, 2016. [Google Scholar]
- Desai, A.; Schwamberger, V.; Herzog, T.; Jänchen, J.; Schmidt, F.P. Modeling of Adsorption Equilibria through Gaussian Process Regression of Data in Dubinin’s Representation: Application to Water/Zeolite Li-LSX. Ind. Eng. Chem. Res. 2019, 58, 17549–17554. [Google Scholar] [CrossRef]
- Kast, W.; Hohenthanner, C.-R. Mass transfer within the gas-phase of porous media. Int. J. Heat Mass Transf. 2000, 43, 807–823. [Google Scholar] [CrossRef]
- Kast, W. Adsorption aus der Gasphase—Ingenieurwissenschaftliche Grundlagen und technische Verfahren; VCH: Weinheim, Germany, 1988. [Google Scholar]
- Kast, W. Der diffusive Stofftransport im Übergansgebiet zwischen Kontinuum und Knudsen-Region. Chem. Ing. Tech. 2001, 73, 1150–1153. [Google Scholar] [CrossRef]
- Girnik, I.S.; Aristov, Y.I. Dynamic optimization of adsorptive chillers: The “AQSOA™-FAM-Z02–Water” working pair. Energy 2016, 106, 13–22. [Google Scholar] [CrossRef]
- Girnik, I.S.; Aristov, Y.I. Dynamics of water vapour adsorption by a monolayer of loose AQSOA™-FAM-Z02 grains: Indication of inseparably coupled heat and mass transfer. Energy 2016, 114, 767–773. [Google Scholar] [CrossRef]
- Bonaccorsi, L.; Bruzzaniti, P.; Calabrese, L.; Freni, A.; Proverbio, E.; Restuccia, G. Synthesis of SAPO-34 on graphite foams for adsorber heat exchangers. Appl. Therm. Eng. 2013, 61, 848–852. [Google Scholar] [CrossRef]
- Shelton, S.V.; Wepfer, W.J.; Miles, D.J. Square wave analysis of the solid-vapor adsorption heat pump. Heat Recover. Syst. CHP 1989, 9, 233–247. [Google Scholar] [CrossRef]
- Sun, L.; Feng, Y.; Pons, M. Numerical investigation of adsorptive heat pump systems with thermal wave heat regeneration under uniform-pressure conditions. Int. J. Heat Mass Transf. 1997, 40, 281–293. [Google Scholar] [CrossRef]












| Sample Name | we55 | we95 | Granules |
|---|---|---|---|
| Support Plate 1 | Sample Carrier 2 | ||
| Length in mm | 50 ± 0.1 | 50 ± 0.1 | 50 ± 0.1 |
| Width in mm | 50 ± 0.1 | 50 ± 0.1 | 50 ± 0.1 |
| Thickness in mm | 2 ± 0.1 | 2 ± 0.1 | - |
| Mass in g | 46.6 ± 0.5 + | 46.6 ± 0.5 + | 20.5 ± 0.5 ++ |
| Sample | |||
| Diameter in mm | 49 ± 0.5 | 48.5 ± 0.5 | - |
| Height in mm | 5.3 ± 0.1 | 3.5 ± 0.1 | 4.9 ± 0.5 |
| Area in cm2 | 18.9 ± 0.4 | 18.5 ± 0.4 | 19.0 ± 0.5 |
| Mass of copper particles in g | 18.4 ± 0.5 | 10.2 ± 0.5 | - |
| Mass of binder in g | 1.29 | 0.75 | - |
| Adsorbent mass (dry) in g | 5.0 ± 0.3 | 3.3 ± 0.2 | 4.8 ± 0.3 |
| Particle size of adsorbent in µm | 400…750 | 63…125 | 400…750 |
| Measurement | [°C] | [°C] | [mbar] |
|---|---|---|---|
| inert-LTJ 1 | 60 | 90 | 44 |
| inert-LTJ 2 | 90 | 60 | 44 |
| Measurement | [°C] | [°C] | [mbar] | [°C] |
|---|---|---|---|---|
| LTJ ads | 93.8 | 49.4 | 17.0 | 14.9 |
| LTJ des | 49.5 | 94.0 | 31.2 | 24.7 |
| Sample Name | we55 | we95 | Granules |
|---|---|---|---|
| Sample Properties | |||
| Thermal mass of support/carrier in J/K | 17.04 | 17.04 | 18.41 |
| Thermal mass of composite/adsorbent in J/K | 12.56 | 7.47 | 4.08 |
| Overall thermal mass in J/K | 29.59 | 24.50 | 22.49 |
| Evaluation Quantities | |||
| Overall thermal mass per sample area in J/(K·cm2) | 1.58 | 1.37 | 1.20 |
| Adsorbent mass per composite volume in kg/m3 | 480 | 510 | 524 |
| Specific thermal mass (STM) of composite in kJ/(kg·K) | 2.51 | 2.26 | 0.85 |
| Property | Value | Source |
|---|---|---|
| Specific heat capacity of adsorbent in J/(kg*K), mean value for temperature range 50…95 °C | 850 | Function [57], data [58] |
| Specific heat capacity of binder in J/(kg*K) | 1000 | estimated |
| Specific heat of copper in J/(kg*K) | 382 | [59] |
| Specific heat of aluminum | 900 | [59] |
| Sample | Thermal Conductivity in W/(m·K) |
|---|---|
| we55 | 1.7 |
| we95 | 1.3 |
| Sample | Measurement | Thermal Conductivity of Composite/Adsorbent in W/(m·K) | Heat Transfer Coefficient between Sample and Carrier Plate in W/(m2·K) | Overall Heat Transfer Resistance in (cm2·K)/W |
|---|---|---|---|---|
| we55 | 60 → 90 °C, N2 44 mbar | 1.9 ± 0.2 | 2400 ± 370 | 14 ± 1 |
| 90 → 60 °C, N2 44 mbar | 2.0 ± 0.2 | 2400 ± 350 | 13 ± 1 | |
| we95 | 60 → 90 °C, N2 44 mbar | 2.3 ± 0.3 | 2100 ± 120 | 10 ± 1 |
| 90 → 60 °C, N2 44 mbar | 1.8 ± 0.2 | 2600 ± 280 | 10 ± 1 | |
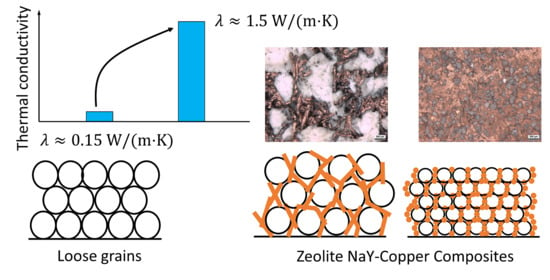
| Granules 400…750 µm | 60 → 90 °C, N2 44 mbar | 0.15 ± 0.02 | 2300 ± 250 | 150 ± 20 |
| 90 → 60 °C, N2 44 mbar | 0.14 ± 0.02 | 2300 ± 250 | 150 ± 20 |
| Sample | Measurement LTJ | in s | in s | in s |
|---|---|---|---|---|
| we55 | ads | 145 | 238 | 129 |
| des | 86 | 125 | 75 | |
| we95 | ads | 1377 | 2352 | 1337 |
| des | 195 | 337 | 176 | |
| Granules | ads | 272 | 447 | 259 |
| des | 290 | 444 | 273 |
| Description | Mass Fraction of Metal/Additives | Particle Diameter | Thermal Conductivity of Adsorbent (Bed) or Adsorbent-Metal Composite in W/(m·K) | Source |
|---|---|---|---|---|
| silicagel-Bed | - | 3…5 mm | 0.1 + | Demir et al. [17] |
| silicagel-Bed | - | 100…160 µm | 0.17 ++ | Kulakowska et al. [20] |
| silicagel-Bed with metallic additives | 5…15% | 3…5 mm | 0.14…0.36 + | Demir et al. [17], Rezk et al. [18] |
| silicagel-Bed with metallic additives or carbon-nanotubes | 5…15% | 100…160 µm | 0.3…0.6 ++ | Kulakowska et al. [20] |
| silicagel/expanded graphite | 10…18 +++ | Eun et al. [21] | ||
| Zeolite with binders | 10…40% | 0.2…0.4 > | Pino et al. [22] | |
| Zeolite NaY Bed | - | 400…750 µm | 0.12…0.16 * | This work |
| Zeotype SAPO-34 on fibrous aluminum structure | 40…70% | 20…50 µm (layer thickness) | 3…6 * | Velte et al. [42], Velte [51] |
| NaY zeolite Granules in copper matrix | 70% | 400…750 µm | 1.8…2.3 * | This work |
| SAPO-34 on expanded natural graphite | up to 24 ** | Bonaccorsi et al. [67] |
| Adsorbent | Material | (w/o Adsorbent) in kJ | in kJ | in kg | in kJ/kg |
|---|---|---|---|---|---|
| Granules NaY | Al | 1.4 | 1.7 | 0.39 | 4.5 |
| Coating TiAPSO | Al | 1.5 | 2.0 | 0.45 | 4.4 |
| sint-struc NaY | Cu | 1.6 | 2.4 | 0.37 | 6.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Velte, A.; Weise, J.; Laurenz, E.; Baumeister, J.; Füldner, G. Zeolite NaY-Copper Composites Produced by Sintering Processes for Adsorption Heat Transformation—Technology, Structure and Performance. Energies 2021, 14, 1958. https://doi.org/10.3390/en14071958
Velte A, Weise J, Laurenz E, Baumeister J, Füldner G. Zeolite NaY-Copper Composites Produced by Sintering Processes for Adsorption Heat Transformation—Technology, Structure and Performance. Energies. 2021; 14(7):1958. https://doi.org/10.3390/en14071958
Chicago/Turabian StyleVelte, Andreas, Jörg Weise, Eric Laurenz, Joachim Baumeister, and Gerrit Füldner. 2021. "Zeolite NaY-Copper Composites Produced by Sintering Processes for Adsorption Heat Transformation—Technology, Structure and Performance" Energies 14, no. 7: 1958. https://doi.org/10.3390/en14071958
APA StyleVelte, A., Weise, J., Laurenz, E., Baumeister, J., & Füldner, G. (2021). Zeolite NaY-Copper Composites Produced by Sintering Processes for Adsorption Heat Transformation—Technology, Structure and Performance. Energies, 14(7), 1958. https://doi.org/10.3390/en14071958