Revisiting the Corresponding-States-Based Correlation for Pool Boiling Critical Heat Flux

Abstract

A corresponding-states correlation for predicting the critical heat flux (CHF) in pool boiling conditions is proposed, and only requires knowledge of physical property constants of the fluid at any fluid temperature: molar mass, critical temperature, critical pressure, and the Pitzer acentric factor. If a fourth corresponding equation of state (EoS) parameter is added, a more accurate CHF correlation is obtained and matches Kutateladze–Zuber prediction within ±10% in the reduced temperature range of 0.55–0.95. This way, CHF can be easily predicted for any reduced temperature within the range of correlation’s validity by only knowing basic properties of the fluid. Additionally, two corresponding-states correlations for determining the capillary length are proposed and also do not rely on any temperature- and pressure-dependent fluid properties. A simpler correlation only using the Pitzer acentric factor is shown to be imprecise, and a more complex correlation also accounting for the fourth corresponding EoS parameter is recommended. These correlations are fundamental for further developments, which would allow for accurate prediction of CHF values on functionalized surfaces through further studies on the influence of interactions of fluid properties with other parameters, such as wetting and active nucleation site density.

1. Introduction

1.1. Critical Heat Flux in Pool Boiling

Pool boiling is a common phenomenon, where phase-change takes place in a pool of macroscopically stationary liquid without the presence of external flow, which would affect the heat transfer phenomena. Engineering applications mostly rely upon the nucleate boiling regime of pool boiling, where high values of the heat transfer coefficient are achievable at relatively small temperature differences between the boiling surface and the liquid bulk. The upper heat flux limit of the nucleate boiling regime is called the critical heat flux (CHF), where the entire boiling surface becomes covered with a vapor film acting as a thermal insulator. This severely decreases the heat transfer intensity during the ensuing transition towards film boiling, and is mostly undesirable. Many widespread technologies rely on boiling heat transfer and tend to operate at high heat flux values (e.g., nuclear reactors, steam boilers, microelectronic cooling systems etc.), making accurate prediction of the CHF value paramount to ensure their safe and efficient operation.

1.2. Existing CHF Correlations

As CHF incipience in a practical application could severely damage equipment and cause process failure, it is imperative to avoid it. For that purpose, one must be able to estimate at what heat flux the CHF might occur to be able to safely dimension the equipment and the boiling process. The first CHF correlation was proposed in the 1950s by Kutateladze [1], who correlated the critical heat flux to be a function of liquid and vapor density (ρ_l and ρ_v), surface tension σ, gravitational acceleration g and latent heat of vaporization Δh_lv alongside a constant K:

$$CHF=K{\rho }_{\mathrm{v}}\Delta h_{\mathrm{lv}}\sqrt[4]{\frac{\sigma g\left({\rho }_{\mathrm{l}}-{\rho }_{\mathrm{v}}\right)}{{\rho }_{\mathrm{v}}^2}} .$$

(1)

Kutateladze proposed the empirically obtained value of the constant K (also known as the Kutateladze number) to be 0.16.

Later in the same decade, Zuber [2] developed a correlation for estimating the CHF value, which is based on the hydrodynamic instability theory, and is arguably the most well-known CHF correlation to date. In derivation of his theory, Zuber assumed that Taylor’s and Helmholtz’s instability were the main factors behind the CHF incipience. Vapor jets on the surface were assumed to be spaced on a square grid in accordance with the Taylor’s wavelength, whereas instability of the vapor jets was assumed to be governed by the Helmholtz’s wavelength, stemming from the vapor velocity becoming too great. Zuber assumed that the jet diameter is one half of the most dangerous Taylor’s wavelength, and theoretically derived the same expression as Kutateladze [Equation (1)], but with a different value of the constant (i.e., the Kutateladze number), which was to be π/24 (approximately 0.131). We will refer to the correlation given in Equation (1) as the Kutateladze–Zuber correlation in the rest of the manuscript.

The CHF correlation was further developed by Lienhard and Dhir [3], who observed that the CHF value is also dependent upon the heater geometry. Through modification of Zuber’s theory, Lienhard and Dhir obtained a Kutateladze number of 0.149 for an infinite flat plate heater. They also found that CHF appears to increase on small heaters [4], which was shown to depend on the ratio between the heater’s characteristic dimension and the so-called capillary length b, calculated as:

$$b=\sqrt{\frac{\sigma }{g\left({\rho }_{\mathrm{l}}-{\rho }_{\mathrm{v}}\right)}} .$$

(2)

Alternative theories on the reason for CHF incipience have also been proposed. For example, dryout of the liquid macrolayer formed below large coalesced bubbles might be blamed for CHF onset [5,6].

Several correlations for predicting the CHF value were proposed since the initial publications by Kutateladze and Zuber. The latter correlation only takes into account the hydrodynamic aspects of the CHF incipience, and therefore fails to account for other phenomena, such as the effect of heater size (as mentioned above), heater’s surface properties (such as its wettability, roughness, and wickability), thermal properties of the substrate (e.g., its effusivity) etc. New correlations aim to tackle one or more of these missing aspects to possibly provide a generalized model for CHF description. One such model was proposed by Bar-Cohen’s team [7,8,9]:

$$CHF=\frac{\pi }{24}{\rho }_{\mathrm{v}}\Delta h_{\mathrm{lv}}\sqrt[4]{\frac{\sigma g\left({\rho }_{\mathrm{l}}-{\rho }_{\mathrm{v}}\right)}{{\rho }_{\mathrm{v}}^2}}\times \mathrm{fn}\left(t\sqrt{{\rho }_{\mathrm{h}}{c}_{p,\mathrm{h}}{k}_{\mathrm{h}}}\right)\times \mathrm{fn}\left(L^{\prime }\right)\times \mathrm{fn}\left(\Delta T_{\mathrm{sub}}\right).$$

(3)

The latter correlation includes the Kutateladze–Zuber correlation with an addition of functions that account for the thickness and thermal effusivity [10] of the heater [$\mathrm{fn}\left(t\sqrt{{\rho }_{\mathrm{h}}{c}_{p,\mathrm{h}}{k}_{\mathrm{h}}}\right)$], the dimensionless length of the heater [$\mathrm{fn}\left(L^{\prime }\right)$, defined in Equation (4) as the ration between the length of the heater and the capillary length], and the liquid bulk’s subcooling [$\mathrm{fn}\left(\Delta T_{\mathrm{sub}}\right)$].

$$L^{\prime }=\frac{L}{b}.$$

(4)

Recent progress in the field of identifying surface properties affecting the CHF value came from Rahman et al. [11], who found that wickability of the boiling surface represents a key factor in enhancing the CHF value. They propose that a “wicking” Kutateladze number should be defined as:

$$K_{\mathrm{W}}=K\left(1+Wi\right),$$

(5)

where Wi is the dimensionless wicking number. The latter accounts for heat dissipation associated with wicking of liquid across the boiling surface and is calculated through maximum wicked volume flux ${\dot{V}}_0^{″}$ (experimentally determined for a given surface) as:

$$Wi=\frac{{\dot{V}}_0^{″}{\rho }_{\mathrm{l}}}{{\rho }_{\mathrm{v}}^{0.5}{\left[\sigma g\left({\rho }_{\mathrm{l}}-{\rho }_{\mathrm{v}}\right)\right]}^{0.25}}.$$

(6)

The latter correlation is able to explain both why hydrophilic surfaces offer enhanced critical heat flux, exceeding the Kutateladze–Zuber limit, and that all superhydrophilic surfaces do not offer the same performance due to different wicking volume flux despite the same contact angle value of ~0°.

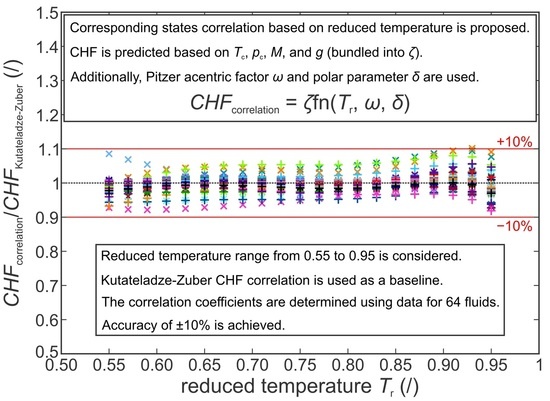
1.3. Corresponding States Correlations

Currently established correlations such as the Kutateladze–Zuber prediction allow for the CHF to be estimated for given experimental conditions by accounting for the fluid properties at the given saturation temperature and pressure. Further improvement of the CHF prediction’s accuracy for functionalized surfaces requires additional parameters to be measures, such as the aforementioned wicking volume flux. However, even the basic Kutateladze–Zuber correlation can be used to estimate the CHF value in dimensioning of common systems involving nucleate pool boiling heat transfer. This, however, requires the user to know the fluid properties, such as the surface tension, liquid and vapor density, and latent heat of vaporization, for any given operating pressure and temperature. While modern databases, such as REFPROP, allow for these values to be easily obtained for many common liquids in any desired state, it can be a hassle to find theirs values for less common or new fluids. Furthermore, they need to be recalculated if the operating point (i.e., saturation pressure or temperature) is changed. Therefore, a generalized description relying on a common behavior of fluids would be beneficial. For this purpose, the corresponding states theorem can be applied to compare the fluids at a given reduced temperature and/or pressure and extrapolate their behavior to other states. Reduced temperature and reduced pressure are defined as the ratio between the given value of the parameter and its critical value (i.e., the critical temperature T_c or critical pressure p_c):

$$T_{\mathrm{r}}=T/T_{\mathrm{c}} \mathrm{and}$$

(7)

$$p_{\mathrm{r}}=p/p_{\mathrm{c}}.$$

(8)

Several proposition for using corresponding states to correlate the CHF values were made as early as in 1960s [12,13]. However, these correlations are based on reduced pressure, whereas reduced temperatures are somewhat more practical for engineering use. Furthermore, the existing correlations based on thermodynamic similarity require data on CHF at a certain reduced pressure, usually at p_r = 0.1 [14], together with the reduced pressure function or the reduced temperature function [13], or knowledge of additional group parameters that are hard to determine, such as the Parachor [12] or the vapor-pressure parameter [15]. In all cases, the physical properties of the fluid are also required to determine the capillary length given in Equation (2) to adjust the predicted values for finite heaters. Finally, these correlations are based on reduced pressure instead of reduced temperature.

1.4. Aim of This Study

Currently established correlations for CHF predictions require knowledge of fluid properties under the given operating conditions, which might not be easily obtained for a given fluid and also change with a change in operating point of the system. Therefore, the aim of this study is to develop a corresponding-sates-based correlation to predict the CHF value in pool boiling using reduced temperature as the main input within the reduced temperature range between 0.55 and 0.95, which is the most common range within which a vapor–liquid equilibrium is possible for most fluids. The developed correlation’s predictions are compared to the Kutateladze–Zuber prediction for the same fluids at given operating conditions to evaluate its accuracy. Furthermore, corresponding-states-based correlation is also provided for determining the capillary length using reduced temperature and fluid constants, which is a vital part of many correlations that also take into account enhanced CHF on functionalized surfaces.

2. Proposed Correlation

2.1. Accounting for Fluid Properties and Gravity

Taking into account Gibbs’ rule of phases [16] for one component with two phases (i.e., a single component fluid at liquid-vapor equilibrium), only one independent thermodynamic quantity is present. The following equation of state can, therefore, be written for both non-polar and polar fluids:

$$\mathrm{F}\left(T_{\mathrm{r}},\omega ,\delta \right)=0.$$

(9)

The Pitzer acentric factor, ω, is defined by the reduced saturation pressure at a reduced saturation temperature of T_r = 0.7:

$$\omega =-1-\log \left(p_{\mathrm{r}}@T_{\mathrm{r}}=0.7\right).$$

(10)

The fourth corresponding state parameter δ is defined in terms of the reduced pressure of saturated fluid at two reduced temperature values (T_r = 0.7 and 0.75), making it a better descriptor especially for polar fluids:

$$\delta =49.94330\ln \left(p_{\mathrm{r}}@T_{\mathrm{r}}=0.7\right)-67.18390\ln \left(p_{\mathrm{r}}@T_{\mathrm{r}}=0.75\right)-5.976280.$$

(11)

ω and δ define the corresponding equation of state (EoS). These parameters are given in [17] for over 100 fluids. From the viewpoint of the corresponding-states principle, the choice of reduced temperatures is better than that of reduced pressures, since the additional parameters of the corresponding EoS are defined at a constant reduced temperature. As can be seen from Figure 1a, at constant pressure, e.g., at p_r = 0.1, the reduced temperature will change, depending on additional parameters ω and δ. The dependence of T_r @ p_r = 0.1 on ω and δ is given from the EoS in the following equation, the coefficients of which (a₁ to a₆) are provided in

Table 1. Coefficients of Equation (12).

Coefficient	Value
a1	0.092756
a2	−0.190985
a3	0.225279
a4	0.00225388
a5	−0.00316658
a6	0.698207

:

$$T_{\mathrm{r}} \left(@p_{\mathrm{r}}=0.1\right)=a_1{\omega }^3+a_2{\omega }^2+a_3\omega +a_4\delta +a_5\delta \omega +a_6.$$

(12)

The coefficients were obtained by fitting Equation (12) using data for 142 fluids in the REFPROP 10.0 database [18]. The match between REFPROP-calculated values and values predicted using Equation (12), together with coefficients from Table 1 is shown in Figure 1b.

2.2. CHF Correlation

The influence of thermodynamic and transport properties of the fluid on the CHF is based upon the Kutateladze–Zuber correlation [Equation (1)]. Using the Brock and Bird equation for the surface tension of non-polar and slightly polar fluids, including the Pitzer acentric factor [19], and with the introduction of the reduced thermodynamic values Δh_lv/(RT_c), ${\nu }_{\mathrm{rl}}^{*}$ and ${\nu }_{\mathrm{rv}}^{*}$, the influence of the fluid properties can be expressed as:

$$CHF=\frac{0.131T_{\mathrm{c}}^{\frac{1}{3}}{p}_{\mathrm{c}}^{\frac{11}{12}}{g}^{\frac{1}{4}} }{M^{\frac{1}{4}}}{\left[R\left(0.228+0.303\omega \right){10}^{-6}\right]}^{\frac{1}{4}}\left(\frac{\Delta h_{\mathrm{lv}}}{R{T}_{\mathrm{c}}}\right)\frac{1}{{\nu }_{\mathrm{rv}}^{*}}{\left[\frac{{\tau }^{\frac{11}{9}}\left({\nu }_{\mathrm{rl}}^{*}-{\nu }_{\mathrm{rv}}^{*}\right){\left({\nu }_{\mathrm{rl}}^{*}+{\nu }_{\mathrm{rv}}^{*}\right)}^2}{{\nu }_{\mathrm{rl}}^{*}{\nu }_{\mathrm{rv}}^{*}}\right]}^{1/4} ,$$

(13)

where:

$$\tau =1-T_{\mathrm{r}}.$$

(14)

The Lee and Kesler [20] three-parameter corresponding EoS was used to determine the reduced thermodynamic properties. Equation (13) simplifies to:

$$CHF=\zeta \mathrm{fn}\left(T_r,\omega \right),$$

(15)

while a modified version, which also accounts for δ, was also evaluated:

$$CHF=\zeta \mathrm{fn}\left(T_r,\omega ,\delta \right).$$

(16)

In both of the aforementioned cases, the fn(T_r, ω) or fn(T_r, ω, δ) were constructed using τ as defined previously and by taking into account various combinations and exponents of both EoS parameters (ω and δ) and τ.

The fluid property constants and gravity are taken into account in a separate function, which only depends on the used fluid (its M, T_c, p_c) and gravity (value of g):

$$\zeta =T_c^{\frac{1}{3}}{p}_c^{\frac{11}{12}}{g}^{\frac{1}{4}}{M}^{-\frac{1}{4}}\hspace{1em}\left[{\mathrm{K}}^{\frac{1}{3}}{\mathrm{kg}}^{\frac{3}{4}}{\mathrm{kmol}}^{\frac{1}{4}} {\mathrm{m}}^{-\frac{3}{4}} {\mathrm{s}}^{-\frac{5}{2}}\right].$$

(17)

2.3. Capillary Length Correlation

An objective of the current study is to also establish a corresponding-state-based correlation to determine the value of the capillary length at any given reduced temperature (between 0.55 and 0.95), without knowing the values of fluid transport and thermal properties. The capillary length correlation is based on using the Lee and Kesler EoS and the Brock and Bird equation for surface tension and, with the use of the corresponding-states correlation, was approximated as:

$$b=\xi \mathrm{fn}\left(T_{\mathrm{r}}, \omega \right) \mathrm{and}$$

(18)

$$b=\xi \mathrm{fn}\left(T_{\mathrm{r}}, \omega , \delta \right),$$

(19)

where the first equation only accounts for the Pitzer acentric factor, while the second equation also includes the fourth corresponding EoS parameter δ. In both cases, fluid constants and gravity are bundled into the following constant (for each fluid under given gravity):

$$\xi =T_{\mathrm{c}}^{\frac{2}{3}}{p}_{\mathrm{c}}^{-\frac{1}{6}}{M}^{-\frac{1}{2}}{g}^{-\frac{1}{2}} \left[{\mathrm{K}}^{\frac{2}{3}}{\mathrm{kmol}}^{\frac{1}{2}}{\mathrm{s}}^{\frac{4}{3}}{\mathrm{kg}}^{-\frac{2}{3}}{\mathrm{m}}^{-\frac{1}{3}}\right].$$

(20)

2.4. Fluid Properties

Fluid properties, which were used to fit the aforementioned functions, were determined from REFPROP 10.0 database, and are listed in

Table 2. Fluid properties of 64 fluids used to establish the proposed correlations (listed alphabetically).

Fluid	M (kg kmol−1)	Tc (K)	pc (MPa)	ω (/)	δ (/)
acetone	58.0791	508.1000	4.6924	0.3062	0.6657
ammonia	17.0305	405.5600	11.3634	0.2555	0.5256
benzene	78.1118	562.0200	4.9073	0.2109	0.2045
n-butane	58.1222	425.1250	3.7960	0.2007	0.3517
1-butene	56.1063	419.2900	4.0051	0.1917	0.3285
carbon monoxide	28.0101	132.8600	3.4940	0.0498	−0.0180
chlorobenzene	112.5570	632.3500	4.5206	0.2530	0.4733
cyclobutene	54.0904	448.0000	5.1495	0.1634	0.2506
cyclohexane	84.1595	553.6000	4.0805	0.2095	0.1121
cyclopentane	70.1329	511.7200	4.5828	0.2018	0.4945
decane	142.2817	617.7000	2.1030	0.4882	0.4148
ethane	30.0690	305.3220	4.8722	0.0994	0.2086
ethanol	46.0684	514.7100	6.2680	0.6462	−0.0265
ethylbenzene	106.1650	617.1200	3.6224	0.3049	0.4870
ethylene	28.0538	282.3500	5.0418	0.0865	0.0890
ethylene glycol	62.0678	719.0000	10.5087	0.6185	1.5585
heptane	100.2020	540.2000	2.7357	0.3489	0.3928
hexane	86.1754	507.8200	3.0441	0.3002	0.4009
hydrogen	2.0159	33.1450	1.2964	−0.2187	−0.0297
isobutane	58.1222	407.8100	3.6290	0.1835	0.2135
isobutene	56.1063	418.0900	4.0098	0.1925	0.2606
isohexane	86.1754	497.7000	3.0400	0.2796	0.3630
isooctane	114.2285	544.0000	2.5720	0.3034	0.3995
isopentane	72.1488	460.3500	3.3780	0.2273	0.3356
methane	16.0428	190.5640	4.5992	0.0114	0.1310
methanol	32.0422	513.3800	8.2159	0.5620	1.3779
nitrogen	28.0135	126.1920	3.3958	0.0372	0.0532
Novec 649	316.0444	441.8100	1.8690	0.4710	0.0535
octane	114.2290	568.7400	2.4836	0.3974	0.4038
oxygen	31.9988	154.5810	5.0430	0.0222	0.0747
pentane	72.1488	469.7000	3.3675	0.2509	0.3499
perfluorobutane	238.0270	386.3260	2.3224	0.3723	0.1872
Perfluorohexane *	338.0420	448.0000	1.7416	0.4968	0.2196
perfluoropentane	288.0340	421.0000	2.0630	0.4361	0.2429
propane	44.0956	369.8900	4.2512	0.1521	0.2358
propylcyclohexane	126.2392	630.8000	2.8600	0.3261	0.2742
propylene	42.0797	364.2110	4.5550	0.1460	0.2020
R11	137.3680	471.1100	4.4076	0.1887	0.1976
R113	187.3750	487.2100	3.3922	0.2525	0.2267
R115	154.4664	353.1000	3.1290	0.2483	0.3508
R12	120.9130	385.1200	4.1361	0.1794	0.2565
R123	152.9310	456.8310	3.6618	0.2819	0.2556
R124	136.4750	395.4250	3.6243	0.2880	0.2439
R1243zf	96.0511	376.9300	3.5179	0.2602	0.3909
R125	120.0214	339.1730	3.6177	0.3052	0.2487
R13	104.4590	302.0000	3.8790	0.1723	0.1786
R1336mzz(Z)	164.0560	444.5000	2.9030	0.3859	0.3601
R134a	102.0320	374.2100	4.0593	0.3267	0.3621
R13I1	195.9104	396.4400	3.9530	0.1761	0.2918
R14	88.0100	227.5100	3.7500	0.1785	0.2667
R141b	116.9496	477.5000	4.2120	0.2195	0.1278
R142b	100.4950	410.2600	4.0550	0.2320	0.2752
R143a	84.0410	345.8570	3.7610	0.2613	0.5057
R152a	66.0510	386.4110	4.5168	0.2750	0.5161
R161	48.0595	375.2500	5.0460	0.2194	0.4317
R21	102.9200	451.4800	5.1812	0.2061	0.0549
R22	86.4680	369.2950	4.9900	0.2207	0.2361
R227ea	170.0289	374.9000	2.9250	0.3575	0.2339
R23	70.0139	299.2930	4.8320	0.2628	0.4858
R32	52.0240	351.2550	5.7820	0.2767	0.6861
R41	34.0329	317.2800	5.8970	0.2002	0.7162
RE347mcc **	200.0548	437.7000	2.4782	0.4033	0.1659
toluene	92.1384	591.7500	4.1263	0.2655	0.4907
water	18.0153	647.0960	22.0640	0.3439	0.9998

* FC-72, ** HFE-7000.

. In total, 64 fluids were considered, including cryogens (hydrogen, nitrogen, methane, etc.), alcohols and other common hydrocarbons (methanol, ethanol, pentane, hexane, etc.), common refrigerants (R12, R123, R134a, R227ea, etc.), common dielectrics (perfluorohexane [FC-72], Novec 649 and RE347mcc [HFE-7000]), and water.

3. Results and Discussion

3.1. The Zeta Function

Figure 2 shows the evaluation of the zeta function, as defined in Equation (17), as a function of molar mass of the fluid (Figure 2a), critical temperature (Figure 2b), and critical pressure (Figure 2c). In all cases, terrestrial gravity (g = 9.81 m s⁻²) is considered.

It is evident that the value of the zeta function decreases with increasing molar mass of the fluid with an obvious outlier (hydrogen). Furthermore, the value of the zeta function increases exponentially with increasing critical pressure. An attempt was made to use this dependence to describe the zeta function solely through the critical pressure of the fluid and the gravitational acceleration, but the CHF correlations established using this principle showed large and inconsistent deviation from the Kutateladze–Zuber correlation, and this approach was therefore abandoned in favor of describing the zeta function by also using the fluid’s molar mass and critical temperature.

3.2. Evaluation of the CHF Correlation

The following correlation was established to correlate the CHF value in the reduced temperature range between 0.55 and 0.95 by only accounting for the Pitzer acentric factor:

$$CHF=0.131\zeta \tau \exp \left[a_1+a_2\tau +a_3{\tau }^2+a_4{\tau }^3+\omega \left(a_5+a_6{\tau }^3\right)+{\omega }^2\left(a_7\tau +a_8{\tau }^2\right)\right]$$

(21)

The evaluated constants providing the best fit (using the least-square method) for 64 fluids are listed in

Table 3. Coefficients of Equation (21).

Coefficient	Value
a1	2.4766
a2	−10.3499
a3	19.4918
a4	−26.4745
a5	1.4409
a6	−24.4247
a7	−8.7556
a8	14.0273

.

A 3D plot of the fn(T_r,ω) is shown in Figure 3. It is evident that the highest CHF is expected at high values of the Pitzer acentric factor at high values of reduced temperature. At lower values of ω, the maximal value of the function is shifter towards lower reduced temperature values (approx. 0.83–0.85).

An evaluation of the CHF correlation defined through Equation (21) is shown in Figure 4a, where the ratio between the CHF predicted by Equation (21) and calculation using the Kutateladze–Zuber equation [Equation (1) with K = 0.131] is shown for 64 fluids in the reduced temperature range between 0.55 and 0.95.

It is evident that Equation (21) provides CHF predictions close to those predicted by the Kutateladze–Zuber correlation, but some noticeable deviations are observable. At low reduced temperature values, the proposed correlation mostly underpredicts the CHF value with the most obvious deviation for perfluorohexane (FC-72). However, the CHF values for hydrogen are significantly overpredicted within the same range of T_r. All predictions are within ±10% of the Kutateladze–Zuber correlation for reduced temperatures between approx. 0.67 and 0.95, although the deviations increase at high T_r values as the critical point is approached. This also agrees with common experimental observations of significant deviations from the Kutateladze–Zuber correlation at reduced temperatures above 0.95 (which generally match high reduced pressure values).

Figure 4b shows the comparison between CHF values calculated using the Kutateladze–Zuber equation and predicted through the present correlation [Equation (22)]. The overall agreement is good with an R² value of 0.9990.

The second CHF correlation also takes into account the fourth corresponding EoS parameter δ and is aimed at improving the accuracy to an agreement with the Kutateladze–Zuber prediction within ±10% throughout the entire range of investigated reduced temperatures. The correlation is given in the following form:

$$CHF=0.131\zeta \tau \exp \left[a_1+a_2\tau +a_3{\tau }^2+a_4{\tau }^3+\omega \left(a_5+a_6{\tau }^3\right)+{\omega }^2\left(a_7\tau +a_8{\tau }^2\right)+\delta \left(a_9+a_{10}\delta +a_{11}\tau +a_{12}{\tau }^2+a_{13}{\tau }^3\right)\right],$$

(22)

while its coefficients can be found in

Table 4. Coefficients of Equation (22).

Coefficient	Value
a1	2.4326
a2	−9.6663
a3	17.1783
a4	−24.6961
a5	1.3267
a6	−18.5745
a7	−7.1314
a8	8.9765
a9	0.1135
a10	−0.0098
a11	−1.1163
a12	3.6533
a13	−4.5620

.

Figure 5a shows the ratio between the CHF predicted by Equation (22) and calculated using the Kutateladze–Zuber equation [Equation (1) with K = 0.131] for 64 fluids in the reduced temperature range between 0.55 and 0.95. It is evident that including the fourth EoS parameter δ improves the quality of the fit with all values falling within ±10% of the the Kutateladze–Zuber prediction. This is further backed up by results in Figure 5b, which show that the agreement of the proposed correlation given by Equation (22) with the Kutateladze–Zuber correlation is excellent, with an R² value of 0.9991.

To predict the reduced temperature, at which maximal CHF value can be expected, the following two correlations were derived, both with an R² value of >0.99:

$$T_{\mathrm{r}}\left(CHF=\max \right)=0.8342+0.1039\omega \mathrm{and}$$

(23)

$$T_{\mathrm{r}}\left(CHF=\max \right)=0.8352+0.0338\omega +0.0616\delta .$$

(24)

The predicted reduced temperatures for which maximal CHF is expected agree with previous observations [12,21]. Equation (23) is also shown in Figure 3 as the solid black line.

3.3. Evaluation of the Capillary Length Correlation

The following correlation was established to correlate the capillary length value in the reduced temperature range between 0.55 and 0.95 by only accounting for the Pitzer acentric factor:

$$b=\xi \left(a_1+a_2\omega \right){\tau }^{\left(a_3+a_4\omega \right)},$$

(25)

with the fitted coefficients available in

Table 5. Coefficients of Equation (25).

Coefficient	Value
a1	0.013929
a2	−0.004111
a3	0.500811
a4	−0.224784

.

The second correlation for the capillary length also accounts for the values of δ. The proposed expression has the following value, while its coefficients are given in

Table 6. Coefficients of Equation (26).

Coefficient	Value
a1	0.011998
a2	0.008519
a3	−0.026925
a4	0.009959
a5	0.020118
a6	0.023613
a7	−0.067397
a8	0.422018
a9	0.161405
a10	−0.235347
a11	0.157144

:

$$b=\xi \left[a_1+\delta \left(a_2+a_3\delta +a_4{\delta }^3+a_5\omega +a_6\omega \delta +a_7{\omega }^2\delta \right)\right]{\tau }^{\left[a_8+\delta \left(a_9+a_{10}\delta +a_{11}\omega \right)\right]}.$$

(26)

The match between correlated capillary length values and calculated values at a given reduced temperature is shown in Figure 6a for the correlation only accounting for ω [Equation (25)], and in Figure 7a for the correlation also accounting for δ [Equation (26)]. Equation (25) provided a worse fit with deviations from the calculated value of the capillary length exceeding ±20%. We therefore conclude that the fourth EoS parameter (δ) needs to be taken into account to accurately correlate the value of the capillary length. Using Equation (26), deviations are much smaller, and mostly fall within ±10% of the calculated value with slightly larger deviations at high values of reduced temperature (i.e., at T_r > 0.9).

In both cases, Equations (25) and (26) match the calculated data reasonably well, which are shown in Figure 6b and Figure 7b. If δ is not taken into account, an R² value of only 0.9491 was obtained, while a much better value of R² = 0.9931 was obtained for the second correlation given by Equation (26), which accounts for both ω and δ.

3.4. CHF Prediction for Boiling on Functionalized Surfaces

Values predicted by the second CHF correlation [Equation (22)] were compared to experimentally determined values for different fluids at different reduced temperatures. Specifically, data for ethanol [22,23], pentane [24,25], perfluorohexane [26], R123 [27], R1234yf [28], R134a [28], and water [29,30,31,32] was sourced from literature. The results are shown in Figure 8. CHF values measured on plain (untreated) surfaces are compared to values measured on functionalized surfaces, prepared using one or more surface modification techniques, which were all shown to enhance the CHF value.

The results in Figure 8 show that CHF values for plain surfaces match the values predicted by the newly proposed correlation well. However, the proposed correlation is unable to capture the effects of surface functionalization, which importantly increase the CHF value. For this purpose, additional (sub)correlations need to be established, but the foundation for this purpose is readily provided by the means of Equation (26), which allows for the calculation of the capillary length without knowing the temperature- and pressure-dependent fluid properties for the given operating conditions.

4. Conclusions

From the viewpoint of the corresponding-states principle, the use of reduced temperatures is better than that of reduced pressure, since most parameters of the corresponding-states correlation are determined at a constant reduced temperature. A corresponding-states correlation for predicting the CHF value in pool boiling conditions is proposed, and only requires knowledge of physical property constants of the fluid at any fluid temperature: molar mass, critical temperature, critical pressure, and the Pitzer acentric factor. If a fourth corresponding EoS parameter δ is added, a more accurate CHF correlation is obtained, and matches the Kutateladze–Zuber prediction within ±10% in the reduced temperature range of 0.55–0.95. This way, CHF can be easily predicted for any reduced temperature within the range of correlation’s validity by only knowing basic properties of the fluid.

Similarly, two corresponding-states correlations for estimating the capillary length are proposed, and also do not require evaluation of any temperature- and pressure-dependent fluid properties. A simpler correlation only accounting for the Pitzer acentric factor was shown to be imprecise, and a more complex correlation also accounting for the fourth corresponding EoS parameter is recommended. Through these correlations, foundations are laid for further developments, which would allow for accurate prediction of CHF values on functionalized surfaces, which is not possible with the current correlations.

Further studies of the influence of interactions of fluid properties with other parameters, such as wetting, active nucleation site density, and adsorption, are necessary, especially at low reduced temperatures. The presented method with the use of approximate corresponding-states correlations through the calculation of reduced thermodynamic quantities with the corresponding-states equations is also appropriate for other problems within the field of heat transfer, where knowledge on thermodynamic properties of the fluid is necessary.