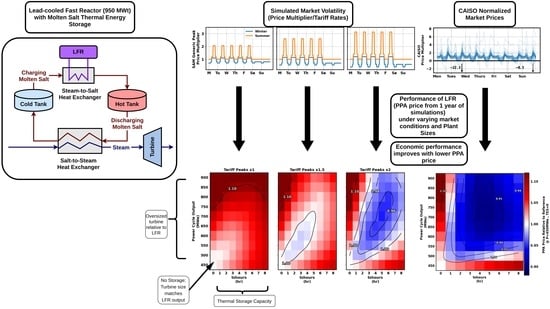
Dispatch Optimization, System Design and Cost Benefit Analysis of a Nuclear Reactor with Molten Salt Thermal Storage
Abstract
:1. Introduction
2. Methods
2.1. Reactor and Plant Assumptions
- better fuel utilization, lower waste production, and the capability to operate at higher temperatures with fast neutron spectrum operation;
- ability to operate coolant at atmospheric pressure with more compact infrastructure; and
- inherent safety mechanics due to high thermal inertia from thermal capacity and larger coolant mass, as well as retention of radioactive isotopes by lead in case of severe accident.
2.2. Market Pricing and Economic Structure
2.3. Mathematical Formulation of Dispatch Optimization Problem
2.4. Implementation of Optimal Dispatch in Engineering Model
3. Results
- the nominal generated electric power from the turbine;
- the capacity of the molten salt tanks; and
- the market pricing scenarios for the plant.
3.1. Load Profiles for Plant with 700 MWe, 2 h of TES, under SAM Tariff Rates
3.2. Load Profiles for Plant wtih 800 MWe, 6 h of TES, under SAM Tariff Rates
3.3. Load Profiles for Both Plant Cases under CAISO Market Conditions
3.4. Plant Sizing Trade Studies
3.5. Sensitivity Analysis on Thermal Storage Costs
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| NPP | Nuclear power plants |
| VRE | Variable renewable energy |
| CAISO | California Independent System Operator |
| TES | Thermal energy storage |
| CSP | Concentrated solar power |
| LFR | Lead-cooled fast reactor |
| SAM | System Advisor Model |
| sCO | Supercritical CO |
| EES | Engineering Equation Solver |
| OASIS | Open Access Same-time Information System |
| LMP | Locational marginal prices |
| ISO | Independent System Operator |
| PPA | Power purchase agreement |
| MILP | Mixed-integer linear program |
| SSC | SAM Simulation Core |
Appendix A
Appendix A.1. Nuclear Supply and Demand Constraints
Appendix A.2. Nuclear Start-Up Constraints
Appendix A.3. Nuclear Logic Constraints
Appendix A.4. Energy Balance Constraints
References
- Denholm, P.; O’Connell, M.; Brinkman, G.; Jorgenson, J. Overgeneration from Solar Energy in California. A Field Guide to the Duck Chart; No. NREL/TP-6A20-65023; National Renewable Energy Lab.: Golden, CO, USA, 2015; Volume 1. [CrossRef] [Green Version]
- Stansbury, C. Westinghouse Modular Heat Storage: A Flexible Approach to Next Generation Grid Needs. Heat Storage for Gen IV Reactors for Variable Electricity from Base-Load Reactors; Idaho National Laboratory: Idaho Falls, ID, USA, 2019.
- Forsberg, C.; Sabharwall, P.; Sowder, A. Separating Nuclear Reactors from the Power Block with Heat Storage: A New Power Plant Design Paradigm; Idaho National Laboratory: Idaho Falls, ID, USA, 2020.
- Forsberg, C.; Sabharwall, P.; Gougar, H.D. Heat Storage Coupled to Generation IV Reactors for Variable Electricity from Base-load Reactors: Workshop Proceedings: Changing Markets, Technology, Nuclear-Renewables Integration and Synergisms with Solar Thermal Power Systems; Idaho National Laboratory: Idaho Falls, ID, USA, 2019.
- Wald, M. With Natrium, Nuclear Can Pair Perfectly with Energy Storage and Renewables. NEI. 2020. Available online: https://www.nei.org/news/2020/natrium-nuclear-pairs-renewables-energy-storage (accessed on 20 March 2022).
- USNC. USNC Micro Modular Reactor (MMR™ Block 1) Technical Information; USNC: Seattle, WA, USA, 2021. [Google Scholar]
- Oh, S.; Lee, J.I. Performance Analysis of Thermal Energy Storage System For Nuclear Power Plant Application; Korean Nuclear Society: Seoul, Korea, 2021. [Google Scholar]
- Alameri, S.A.; King, J.C. A Coupled Nuclear Reactor Thermal Energy Storage System for Enhanced Load Following Operation. In 2013 International Nuclear Atlantic Conference; ABEN: Recife, PE, Brazil, 2013; pp. 173–182. [Google Scholar]
- Romanos, P.; Al Kindi, A.A.; Pantaleo, A.M.; Markides, C.N. Flexible nuclear plants with thermal energy storage and secondary power cycles: Virtual power plant integration in a UK energy system case study. e-Prime-Adv. Electr. Eng. Electron. Energy 2022, 2, 100027. [Google Scholar] [CrossRef]
- Stansbury, C.; Smith, M.; Ferroni, P.; Harkness, A.; Franceschini, F. Westinghouse Lead Fast Reactor Development: Safety and Economics Can Coexist. In Proceedings of the 2018 International Congress on Advances in Nuclear Power Plants, Charlotte, NC, USA, 8–11 April 2018. [Google Scholar]
- Westinghouse Electric Company, U.S.A. Westinghouse Electric Company, U.S.A. Westinghouse Lead Fast Reactor. In Advances in Small Modular Reactor Technology Developments; IAEA Advanced Reactors Information System: Vienna, Austria, 2020; pp. 233–236. [Google Scholar]
- Blair, N.; Diorio, N.; Freeman, J.; Gilman, P.; Janzou, S.; Neises, T.; Wagner, M. System Advisor Model (SAM) General Description (Version 2017.9.5); National Renewable Energy Laboratory Technical Report; National Renewable Energy Lab.: Golden, CO, USA, 2018.
- Smith, C.F.; Halsey, W.G.; Brown, N.W.; Sienicki, J.J.; Moisseytsev, A.; Wade, D.C. SSTAR: The US lead-cooled fast reactor (LFR). J. Nucl. Mater. 2008, 376, 255–259. [Google Scholar] [CrossRef] [Green Version]
- Smirnov, V.; Orlov, V.; Mourogov, A.; Lecarpentier, D.; Ivanova, T. The lead cooled fast reactor benchmark BREST-300: Analysis with sensitivity method. In Nuclear Data Needs For Generation IV Nuclear Energy Systems; World Scientific: Singapore, 2006; pp. 173–182. [Google Scholar]
- Abderrahim, H.A.; Bruyn, D.D.; Dierckx, M.; Fernandez, R.; Popescu, L.; Schyns, M.; Stankovskiy, A.; Eynde, I.; Gert, V.d.; Vandeplassche, D. MYRRHA accelerator driven system programme: Recent progress and perspectives. News High. Educ. Inst. Nucl. Energy 2019, 2, 29–42. [Google Scholar]
- Smith, C.; Cinotti, L. Lead-cooled fast reactor. In Handbook of Generation IV Nuclear Reactors; Pioro, I.L., Ed.; Woodhead Publishing Series in Energy; Woodhead Publishing: Sawston, UK, 2016; Chapter 6; pp. 119–155. [Google Scholar] [CrossRef]
- Alemberti, A.; Smirnov, V.; Smith, C.F.; Takahashi, M. Overview of lead-cooled fast reactor activities. Prog. Nucl. Energy 2014, 77, 300–307. [Google Scholar] [CrossRef]
- Alemberti, A. Lead cooled fast reactors. In Reference Module in Earth Systems and Environmental Sciences; Elsevier: Amsterdam, The Netherlands, 2020. [Google Scholar] [CrossRef]
- Delameter, W.; Bergan, N. Review of the Molten Salt Electric Experiment; Report SAND86-8249; Sandia National Laboratories: Albuquerque, NM, USA, 1986.
- White, B.T.; Wagner, M.J.; Neises, T.; Stansbury, C.; Lindley, B. Modeling of Combined Lead Fast Reactor and Concentrating Solar Power Supercritical Carbon Dioxide Cycles to Demonstrate Feasibility, Efficiency Gains, and Cost Reductions. Sustainability 2021, 13, 12428. [Google Scholar] [CrossRef]
- Hamilton, W.T.; Newman, A.M.; Wagner, M.J.; Braun, R.J. Off-design performance of molten salt-driven Rankine cycles and its impact on the optimal dispatch of concentrating solar power systems. Energy Convers. Manag. 2020, 220, 113025. [Google Scholar] [CrossRef]
- F-Chart. Engineering Equation Solver. 2022. Available online: https://fchartsoftware.com/ees/ (accessed on 20 March 2022).
- Wagner, M.J.; Newman, A.M.; Hamilton, W.T.; Braun, R.J. Optimized dispatch in a first-principles concentrating solar power production model. Appl. Energy 2017, 203, 959–971. [Google Scholar] [CrossRef]
- Kahvecioglu, G.; Morton, D.; Wagner, M. Dispatch Optimization of a Concentrating Solar Power System Under Uncertain Solar Irradiance and Energy Prices. Appl. Energy, 2022; Submitted, In Review. [Google Scholar]
- CAISO. Open Access Same-Time Information System. 2022. Available online: http://oasis.caiso.com/mrioasis/logon.do (accessed on 30 August 2021).
- Kumar, N.; Besuner, P.; Lefton, S.; Agan, D.; Janzou, S.; Hilleman, D. Power Plant Cycling Costs; Technical Report; National Renewable Energy Laboratory: Golden, CO, USA, 2012.
- Cox, J.; Hamilton, W.; Newman, A.; Zolan, A.; Wagner, M. Real-time Dispatch Optimization for Concentrating Solar Power with Thermal Energy Storage. Optim. Eng. 2022; in press. [Google Scholar]
- Bynum, M.L.; Hackebeil, G.A.; Hart, W.E.; Laird, C.D.; Nicholson, B.L.; Siirola, J.D.; Watson, J.P.; Woodruff, D.L. Pyomo—Optimization Modeling in Python, 3rd ed.; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2021; Volume 67. [Google Scholar]
- Forrest, J.; Vigerske, S.; Ralphs, T.; Santos, H.G.; Hafer, L.; Kristjansson, B.; Jpfasano; EdwinStraver; Lubin, M.; Rlougee; et al. Coin-Or/Cbc: Release Releases/2.10.3 2020. Available online: https://zenodo.org/record/3246628#.YoG-DlRBxPY (accessed on 26 October 2020).












| Symbol | Value | Units | Description | Source |
|---|---|---|---|---|
| Dispatch Optimization Parameters | ||||
| 0.00875 | Operating cost of power cycle | Scaled SAM parameters [23,26,27] | ||
| 27,345 | Penalty for power cycle cold start-up | “1 | ||
| 5470 | Penalty for power cycle hot start-up | “ | ||
| 0.00175 | Operating cost of power cycle standby operation | “ | ||
| 0.04375 | Penalty for power cycle production change | “ | ||
| 1.75 | Penalty for power cycle production change past design | “ | ||
| 0.00734 | Operating cost of nuclear plant | Westinghouse estimates | ||
| Engineering Model Financial Parameters | ||||
| 7 | % | Interest rate on financing loan | General assumption | |
| 4 | yr | Construction time | “ | |
| 29.8 | Thermal energy storage cost | Scaled SAM parameters [23,26,27] | ||
| 4150 | Nuclear plant cost including fuel over analysis period | Westinghouse estimates | ||
| Symbol | Units | Description |
|---|---|---|
| Sets | ||
| Set of all time steps within time horizon | ||
| Time-Indexed Parameters | ||
| Available thermal power generated by the nuclear plant in time t | ||
| - | Estimated fraction of time t required for nuclear start-up | |
| - | Cycle efficiency ambient temperature adjustment factor in time t | |
| - | Normalized condenser parasitic loss in time t | |
| Electricity sales price in time t | ||
| Allowable power per period for cycle start-up in time t | ||
| Maximum power production when starting generation in time t | ||
| Maximum power production in time t when stopping generation in time | ||
| Steady-State Parameters | ||
| $ | Conversion factor between unitless and monetary values | |
| Required energy expended to start cycle | ||
| - | Cycle nominal efficiency | |
| Thermal energy storage capacity | ||
| Slope of linear approximation of power cycle performance curve | ||
| Cycle heat transfer fluid pumping power per unit energy expended | ||
| Cycle standby thermal power consumption per period | ||
| Minimum operational thermal power input to cycle | ||
| Cycle thermal power capacity | ||
| Power cycle standby operation parasitic load | ||
| Minimum cycle electric power output | ||
| Cycle electric power rated capacity | ||
| Power cycle ramp-up designed limit | ||
| Power cycle ramp-down designed limit | ||
| Power cycle ramp-up violation limit | ||
| Power cycle ramp-down violation limit | ||
| h | Minimum time to start the nuclear plant | |
| Required energy expended to start nuclear plant | ||
| Nuclear pumping power per unit power produced | ||
| Minimum operational thermal power delivered by nuclear | ||
| Required thermal power for nuclear standby | ||
| Required thermal power for nuclear shut down | ||
| Allowable power per period for nuclear start-up | ||
| Nuclear piping heat trace parasitic loss | ||
| Symbols | Units | Description |
|---|---|---|
| Continuous Variables | ||
| Cycle thermal power utilization at t | ||
| Thermal power delivered by the nuclear at t | ||
| Nuclear start-up power consumption at t | ||
| Power cycle electricity generation at t | ||
| Power cycle ramp-up at t | ||
| Power cycle ramp-down at t | ||
| Power cycle ramp-up beyond designed limit at t | ||
| Power cycle ramp-down beyond designed limit at t | ||
| Energy sold to the grid at t | ||
| Energy purchased from the grid at t | ||
| Cycle start-up energy inventory at t | ||
| Nuclear start-up energy inventory at t | ||
| TES reserve quantity at t | ||
| Binary Variables | ||
| - | 1 if nuclear is generating “usable” thermal power at t; 0 otherwise | |
| - | 1 if nuclear is in standby mode at t; 0 otherwise | |
| - | 1 if nuclear is shutting down at t; 0 otherwise | |
| - | 1 if nuclear is starting up at t; 0 otherwise | |
| - | 1 if nuclear is starting up at t from off; 0 otherwise | |
| - | 1 if nuclear is starting up at t from standby; 0 otherwise | |
| - | 1 if cycle is generating electric power at t; 0 otherwise | |
| - | 1 if cycle is in standby mode at t; 0 otherwise | |
| - | 1 if cycle is shutting down at t; 0 otherwise | |
| - | 1 if cycle is starting up at t; 0 otherwise | |
| - | 1 if cycle is starting up at t from off; 0 otherwise | |
| - | 1 if cycle is starting up at t from standby; 0 otherwise | |
| - | 1 if cycle begins electric power generation at t; 0 otherwise | |
| - | 1 if cycle stops electric power generation at t; 0 otherwise | |
| Market Scenario | Optimal Turbine Size (MWe) | Optimal TES Size (h) | Optimal PPA Price (¢/kWe·h) |
|---|---|---|---|
| SAM Generic Peak ×1.0 | 450 | 0 | 6.54 |
| SAM Generic Peak ×1.5 | 600 | 3 | 6.49 |
| SAM Generic Peak ×2.0 | 700 | 5 | 6.26 |
| CAISO | 750 | 5 | 5.63 |
| Market Scenario | Optimal Turbine Size (MWe) | Optimal TES Size (h) | PPA Price Improvement (%, Relative to Reference) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Performance Penalties: | 0% | 1% | 2.5% | 5% | 0% | 1% | 2.5% | 5% | 0% | 1% | 2.5% | 5% |
| SAM Generic Peak × 1.0 | 450 | ←1 | ← | ← | 0 | ← | ← | ← | 0 | ← | ← | ← |
| SAM Generic Peak × 1.5 | 600 | ← | 450 | ← | 3 | ← | 0 | ← | 1.05 | 0.06 | 0 | ← |
| SAM Generic Peak × 2.0 | 700 | ← | ← | ← | 5 | ← | ← | ← | 4.88 | 3.93 | 2.50 | 0.13 |
| CAISO | 750 | ← | ← | ← | 5 | ← | ← | ← | 10.06 | 9.16 | 7.81 | 5.57 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Soto, G.J.; Lindley, B.; Neises, T.; Stansbury, C.; Wagner, M.J. Dispatch Optimization, System Design and Cost Benefit Analysis of a Nuclear Reactor with Molten Salt Thermal Storage. Energies 2022, 15, 3599. https://doi.org/10.3390/en15103599
Soto GJ, Lindley B, Neises T, Stansbury C, Wagner MJ. Dispatch Optimization, System Design and Cost Benefit Analysis of a Nuclear Reactor with Molten Salt Thermal Storage. Energies. 2022; 15(10):3599. https://doi.org/10.3390/en15103599
Chicago/Turabian StyleSoto, Gabriel J., Ben Lindley, Ty Neises, Cory Stansbury, and Michael J. Wagner. 2022. "Dispatch Optimization, System Design and Cost Benefit Analysis of a Nuclear Reactor with Molten Salt Thermal Storage" Energies 15, no. 10: 3599. https://doi.org/10.3390/en15103599
APA StyleSoto, G. J., Lindley, B., Neises, T., Stansbury, C., & Wagner, M. J. (2022). Dispatch Optimization, System Design and Cost Benefit Analysis of a Nuclear Reactor with Molten Salt Thermal Storage. Energies, 15(10), 3599. https://doi.org/10.3390/en15103599