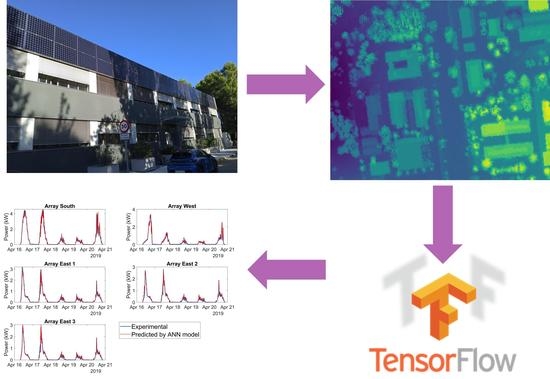
BIPV Modeling with Artificial Neural Networks: Towards a BIPV Digital Twin

Abstract

Modeling the photovoltaic (PV) energy output with high accuracy is essential for predicting and analyzing the performance of a PV system. In the particular cases of building-integrated and building-attached photovoltaic systems (BIPV and BAPV, respectively) the time-varying partial shading conditions are a relevant added difficulty for modeling the PV power conversion. The availability of laser imaging detection and ranging (LIDAR) data to create very-high-resolution elevation digital models can be effectively used for computing the shading at high resolution. In this work, an artificial neural network (ANN) has been used to model the power generation of different BIPV arrays on a 5 min basis using the meteorological and solar irradiance on-site conditions, as well as the shading patterns estimated from a digital surface model as inputs. The ANN model has been validated using three years of 5-min-basis monitored data showing very high accuracy (6–16% of relative error depending on the façade). The proposed methodology combines the shading computation from a digital surface model with powerful machine learning algorithms for modeling vertical PV arrays under partial shading conditions. The results presented here prove also the capability of the machine learning techniques towards the creation of a digital twin for the specific case of BIPV systems that complements the conventional monitoring strategies and can be used in the diagnosis of performance anomalies.

1. Introduction

The decarbonization of the energy sector and the reduction in carbon emissions are included in almost all current energy policies and roadmaps worldwide, with the aim of limiting climate change. Solar photovoltaic (PV) energy is going to play a major role in this energy transformation scenario. Solar PV would supply 25% of the total electricity demand with an estimated installed capacity of 8519 GW by 2050 [1]. Urban areas require an uninterrupted supply of energy, which consumes a very large portion of the primary energy. Therefore, this expected increase in PV deployment will drive a growth in building-integrated photovoltaic (BIPV) and building-attached photovoltaic (BAPV) systems [2,3]. In particular, BIPV modules and systems produce energy and, at the same time, provide additional construction functions; thus, they could reduce the cost of refurbishment and renovation of existing buildings.

Reliable and fast modeling of the electrical performance of PV arrays is crucial for evaluation, operation, forecasting and detection of anomalies. Therefore, a significant effort in modeling PV systems has been made in recent years and several tools have become available to simulate the physical processes involved in the PV energy conversion [4]. However, modeling the electrical performance of PV and BIPV systems in the urban context is very challenging, mainly because of the partial shading conditions that the complex urban topology may cause. The process of BIPV planning and the methods and tools for designing and modeling BIPV systems are currently being analyzed and reviewed within the IEA PVPS Task 15 [5,6].

BIPV systems typically become shaded, either completely or partially, by neighboring buildings, trees and other urban elements. Partial shading is, therefore, a major issue because of the reduction in power output. Consequently, the proper characterization of the shadows along the year is required for both the selection of the most convenient building surfaces and accurate performance modeling [7]. The use of geographic information systems (GIS) enriched with additional remote sensing information (e.g., LIDAR data) can be effectively used in the generation of solar cadasters and shadow studies in urban areas [8,9,10]. A thorough review of BIPV-related methods and tools can be found elsewhere [5,11,12].

Machine learning techniques have recently come up in the energy sector for different applications. Thus, artificial neural networks (ANNs) and other deep learning methods can be used for estimating the PV energy output without the prior knowledge of the PV system parameters [13]. On the other hand, machine learning forecasting techniques have been recently reported in many works as a powerful way to forecast PV power [14,15,16,17,18,19]. In particular, ANNs have shown high accuracy in modeling the PV output compared with some conventional methods [20,21]. Moreover, machine learning and deep learning techniques have recently attracted the attention of many researchers for developing methods aimed at fault diagnosis in PV systems [13,22,23]. Further, the computation efficiency of ANNs is being driven to the digital twin (DT) concept, consisting of a digital reproduction of a PV physical system that can be used, among other purposes, for detecting performance anomalies [24,25]. Approaches based on the DT concept are also being proposed for smart buildings applications [26]. In the case of BIPV applications, a few studies can be found for predicting hourly PV power with ANNs using basic meteorological variables as input, reporting root mean square errors of 4% to 11% [27].

This work presents the use of a single ANN to model five small BIPV systems installed on three façades of the same building using accurate computation of the shading produced by the surrounding buildings and trees and meteorological data. Information on solar irradiance and module temperature, as well as additional variables regarding the angle of incidence of the solar radiation, the azimuth of the façades and the shading (i.e., the fraction of the photovoltaic array surface that is illuminated) was monitored and used as input to the ANN model. Partial shading is a challenge in modeling the BIPV system power and requires detailed and precise knowledge of the shaded area at every timestamp. Therefore, LIDAR data of the surrounding area of the selected building were applied to a GIS tool to build a Digital Surface Model (DSM). A DSM is a high-resolution and detail digital model that captures both the natural and artificial features (e.g., buildings) of the surrounding terrain. The DSM was used as input to a methodology for effectively computing the shades on every façade of the building, with very high spatial resolution, at each timestamp. In the building under study, the east façade is surrounded by deciduous trees that produce inhomogeneous shading patterns on the arrays, making the modeling of the BIPV arrays by either conventional methods or physical models very challenging [28]. The use of LIDAR data for creating a DSM is a very effective way for computing the shades over every façade with high spatial resolution [8]. The modeled ANN, which was trained with two years of monitored data, reached a very good accuracy and performance in modeling the subsequent years of power generation in the building on a 5 min basis. Thus, the main novelty of this work is to use accurate shading estimations at 5 min timestamps with ANN to predict accurately the PV power at every façade for three complete years, evidencing thus the strengths of this kind of model to implement digital twin approaches for PV in buildings.

2. Description of the BIPV Arrays under Study

Building 42 of CIEMAT headquarters (geographic co-ordinates: 40.4555° N and 3.7300° W) is located in a university area of Madrid (Spain). This building was refurbished in 2016, which included the installation of five PV arrays made up of monocrystalline silicon modules on the upper part of its south, west and east façades [29]. Figure 1 shows two pictures of this building with the different BIPV systems. Three identical PV arrays of 7sx2p modules (i.e., seven modules in series and two strings in parallel) were placed at the east façade, while one PV array of 7sx4p modules and another one of 8sx2p modules were installed in the south and west façades, respectively.

Table 1. Technical data of the monitored BIPV system.

Array	Azimuth (°)	Configuration	Module Model	Power (W)	Inverter Model	Inverter Power (kW)
South	172.3	7sx4p	SunPower E18-325	305	Fronius IG Plus 100 V-3	8
West	262.3	8sx2p	SunPower E20-327	327	Fronius IG Plus 50 V-1	4
East 1	82.3	7sx2p	SunPower E20-327	327	Fronius IG Plus 50 V-1	4
East 2	82.3	7sx2p	SunPower E20-327	327	Fronius IG Plus 50 V-1	4
East 3	82.3	7sx2p	SunPower E20-327	327	Fronius IG Plus 50 V-1	4

summarizes the technical details of the whole BIPV installation.

AC output power, voltage and current at the maximum power point, and module temperature of each PV array, as well as the in situ meteorological variables, were monitored. In particular, the global tilt irradiance (90° tilt angle) at the south, west and east directions was monitored through calibrated reference cells placed at the top of a 3-m-high mast on the rooftop of the building. A complete database of all these electrical and meteorological variables was prepared on a 5 min basis.

3. Methodology

3.1. Computation of Shading Parameters

The first step in computing shadows on any part of a single façade in the building is to prepare a digital surface model (DSM). A DSM is a high-resolution digital elevation model of a given geographic area, which includes the elevation of buildings, trees, plants and other elements nearby [30,31]. LIDAR data supplied by the Spanish Geographic Institute (IGN) were used to create a DSM of the surrounding area of the building under study (Figure 2). A line of large deciduous trees can be observed in front of the east façade of the building in the DSM picture. A detailed description of the preparation of the DSM can be found in a previous work done by CIEMAT [28]. A gridded representation of each façade of the building was built from the DSM. The spatial resolution of the grid was 25 cm in length by 50 cm in height; thus, it was possible to identify which parts of the gridded area (hereafter, elements) were occupied by the PV array. For each 25 × 50 cm element of the PV array it was possible to determine shadow casting by computing the maximum elevation in the DSM for every possible azimuth (with an angular resolution of 1°) and comparing it with the sun elevation throughout the year for a 5 min time interval. This can be more effectively achieved by moving the DSM to the Sun azimuth and generating a Boolean variable that takes value 1 if the element is fully illuminated by the sun and 0 if it is completely shaded [30]. Finally, for every time instant in a year, it was possible to identify which elements of the PV array were illuminated and which ones were shaded. Hence, the variable denoted as FS represents the percentage of area which is illuminated in each array for every timestamp.

3.2. Artificial Neural Network (ANN)

A unique sequential neural network model with three hidden layers and one output layer was prepared for modeling the five BIPV arrays using the TensorFlow package. TensorFlow is a powerful open-source software library for numerical computation particularly focused on machine learning algorithms [32]. The hidden layers contained 18, 12 and 6 nodes, respectively. The input layer contained five numerical variables and one single categorical variable. The numerical variables were the plane on the array irradiance (POA), the module temperature (Tm), the ambient temperature (Ta), the illuminated fraction of array (FS) and the cosine of the incident angle (cosAOI). The categorical variable was the façade orientation (i.e., south, west or north) expressed numerically by the azimuth angle of the corresponding façade. Figure 3 shows the scheme of the ANN model. The dataset for training and testing the model consisted of two complete years (2017 and 2018) of 5-min-basis data of the meteorological variables and the output power of each array. POA, Tm, Ta and power were monitored with the inverter of each BIPV system, while FS and cosAOI were calculated for every timestamp from the DSM and the pvlib package [33], respectively.

The 2017–2018 dataset was randomly sorted and divided into a 70% fraction for training the ANN model and a 30% fraction for testing it. Figure 4 shows the performance of this ANN in the training stage using the mean square error (MSE) as loss function. The model converged quickly and both training and testing performances nearly reached 2% of mean square error after 300 epochs.

Figure 5 shows the scatter plot of the modeled versus measured power with the testing dataset, which consisted of 30% of the 5-min-basis data monitored during 2017 and 2018. A good correlation was found between predicted and experimental power values.

In order to explore the relative importance of the input variables in the ANN model, there are several methods and algorithms to quantify the explanatory contributions of the predictor variables in the network. For instance, Olden’s algorithm is able to evaluate artificial neural networks with multiple hidden layers based on the product of the input-hidden and hidden-output connection weights summing the products across all hidden neurons [34]. Figure 6 shows the relative importance of the input variables for the model trained for predicting BIPV array output power. The parameters related to the array orientation (façade azimuth) and the shading of the array (FS) were the most meaningful ones according to Olden’s method.

4. Results

The ANN model, after being trained and tested during the 2017–2018 period, was used to estimate the power output of the five BIPV arrays at 5 min timestamps for almost three years (from January 2019 to December 2021). Figure 7 shows the results of modeling all these arrays with the ANN by means of the scatter plots of modeled versus experimental output power. According to the results shown in the figure, one single ANN model is able to estimate power differencing the orientation of the façade and take into account the partial shading effect. The agreement was very good, although the arrays at the east façade showed higher dispersion. Indeed, the presence of a row of deciduous trees 10 meters away in front of the east façade produced a higher uncertainty in the shadow estimates for this façade compared to the other two. This observation has been already presented in a previous work where the physical modeling of the same arrays was studied [28]. In addition, Figure 8 illustrates the ANN modeling capabilities with respect to the time of day by comparing the monitored and the modeled output power for a few specific days in 2019; as observed, the model precision and accuracy were significant.

In order to assess the performance of the ANN model,

Table 2. Error metrics in the assessment of the ANN model.

Array	MBE (kW)	RMSE (kW)	MAE (kW)	R2
South	0.02	0.19	0.12	0.99
West	0.00	0.11	0.07	0.99
East 1	−0.01	0.17	0.07	0.94
East 2	0.04	0.20	0.08	0.88
East 3	0.00	0.21	0.09	0.89

lists several metrics: mean bias error (MBE), root mean square error (RMSE), mean absolute error (MAE) and coefficient of determination (R²).

Since the energy generation of each BIPV array is different according to the façade orientation, the modeling performance comparison should be complemented with a relative error metric. Thus, the relative mean absolute error in modeling 5-min-basis power data for the arrays was 6.0%, 8.2%, 11.1%, 15.2% and 15.9%, respectively, indicating that the arrays installed in the east façade had higher uncertainties, and, among them, the one placed at the northernmost part of the east façade (array East 3) showed the highest error. This is due to the large number of high trees placed close to the northeast corner of the building (see Figure 2). Nevertheless, in spite of the uncertainty due to the presence of nearby trees, the modeling capability and accuracy of the ANN model is noteworthy. Therefore, this model could be used in diagnosis for detecting abnormal working conditions of any BIPV array.

The impact of including the shadow cast in the ANN is significant and contributes notably to the accuracy in the predictions. This is one of the main hypotheses of this work, and part of the novelty as well. In order to prove this statement, a sensitivity analysis on the role of the input parameter FS was performed in the East 1 array. ANN models with and without using FS as input were trained and tested with the dataset. Figure 9 shows the scatter plots of the performance of each ANN, where the improvement achieved by adding the shadows as input to the ANN is clearly evidenced.

5. Conclusions

Modeling PV power in building façades and BIPV systems requires precise knowledge of shading caused by the surrounding buildings, trees and other urban elements. This implies the modeling of PV module performance under partial shading conditions, which vary along both the day and the year. Moreover, the shading patterns at a given time might be very heterogeneous depending on the surrounding elements to the façade, making performance modeling even more challenging. In this work, a model based on one single artificial neural network (ANN) has been trained and validated with two years of data of a monitored BIPV system consisting of five different arrays placed at the top of the south, west and east façades of a CIEMAT’s building in a university area of Madrid (Spain). Afterwards, the analyzed ANN has been used for modeling the power behavior of all the arrays during three subsequent years (i.e., from 2019 to 2021), and the results showed a prediction of the power of each sub-array on a 5 min basis with high accuracy. The input parameters to this model were divided into two groups. The first group corresponded to PV direct conversion parameters: POA irradiance, module temperature and ambient temperature. The second group corresponded to geometry, orientation and shading of the modules: cosine of the sunlight incident angle, azimuth of the façade and illuminated fraction of the array at every time step.

The analysis of the ANN performance evidenced the significant importance of geometric-related variables, in particular, the proper computation of the shadows. Thus, the use of shadow cast using DSM from LIDAR data as input data in modeling the power of BIPV seems to play a crucial role for the accuracy of BIPV predictions.

Notwithstanding the challenging conditions associated with the dynamic partial shading of the arrays, particularly those installed on the east façade which are facing a long line of large trees nearby, the proposed ANN model was able to estimate the power of each individual PV array with high accuracy, while being an easy-to-implement methodology. The mean relative error (MRE) in predicting power on a 5 min basis ranged approximately from 6% to 15%. Therefore, this kind of model can be used relatively well in digital twin approaches for buildings with BIPV systems, which would allow the diagnosis of anomalous behaviors. In addition, the methodology proposed in this work can be generally extrapolated to any other building whenever LIDAR data are available for proper shading computation. Benchmarking of other different machine learning methods (gradient boost, support vector machine, and random forest) could be interesting for selecting the most appropriate algorithm. Future work will assess this comparison. A further study focused on forecasting with ANNs is also expected as future scope.