Design and Real-Time Implementation of a Control System for SiC Off-Board Chargers of Battery Electric Buses
Abstract
:1. Introduction
2. System Architecture
3. System Modeling and Control Design
3.1. Linear Modeling
3.2. Control Design and Optimization
4. Simulation Results
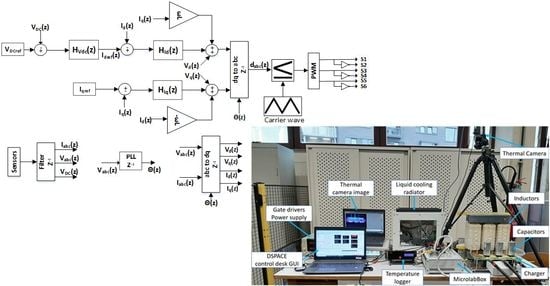
5. Real-Time Control Implementation
5.1. Controller Sampling Time
5.2. Sensors Calibration
5.2.1. Voltage Sensors
5.2.2. Current Sensors
5.3. Phase Lock Loop (PLL)
5.4. PI Controller
5.5. Clarke/Park Transformation
5.6. PWM Signals
6. Experimental Setup and Results
6.1. Experimental Setup
6.2. Experimental Results
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Yilmaz, M.; Krein, P.T. Review of integrated charging methods for plug-in electric and hybrid vehicles. In Proceedings of the 2012 IEEE International Conference on Vehicular Electronics and Safety (ICVES 2012), Istanbul, Turkey, 24–27 July 2012; pp. 346–351. [Google Scholar]
- Hegazy, O.; Van Mierlo, J.; Lataire, P. Design and control of bidirectional DC/AC and DC/DC converters for plug-in hybrid electric vehicles. In Proceedings of the 2011 International Conference on Power Engineering, Energy and Electrical Drives, Malaga, Spain, 11–13 May 2011; pp. 1–7. [Google Scholar]
- Monteiro, V.; Pinto, J.G.; Exposto, B.; Gonçalves, H.; Ferreira, J.C.; Couto, C.; Afonso, J.L. Assessment of a battery charger for electric vehicles with reactive power control. In Proceedings of the IECON 2012—38th Annual Conference on IEEE Industrial Electronics Society, Montreal, QC, Canada, 25–28 October 2012; pp. 5142–5147. [Google Scholar]
- Microsemi, P.P.G. Gallium Nitride (GaN) Versus Silicon Carbide (SiC) in the High Frequency (RF) and Power Switching Applications. Digi-Key. 2014. Available online: https://www.google.com.hk/url?sa=t&rct=j&q=&esrc=s&source=web&cd=&ved=2ahUKEwj9pMrCsoP2AhVWAd4KHei6Ca4QFnoECAQQAQ&url=https%3A%2F%2Fwww.richardsonrfpd.com%2Fdocs%2Frfpd%2FMicrosemi-A-Comparison-of-Gallium-Nitride-Versus-Silicon-Carbide.pdf&usg=AOvVaw04OQ1N7lQjVwJm-D6NBe2e (accessed on 10 February 2022).
- Rasool, H.; El Baghdadi, M.; Rauf, A.M.; Zhaksylyk, A.; Hegazy, O. A Rapid Non-Linear Computation Model of Power Loss and Electro Thermal Behaviour of Three-Phase Inverters in EV Drivetrains. In Proceedings of the 2020 International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Sorrento, Italy, 24–26 June 2020; pp. 317–323. [Google Scholar]
- Chakraborty, S.; Vu, H.-N.; Hasan, M.M.; Tran, D.-D.; El Baghdadi, M.; Hegazy, O. DC-DC converter topologies for electric vehicles, plug-in hybrid electric vehicles and fast charging stations: State of the art and future trends. Energies 2019, 12, 1569. [Google Scholar] [CrossRef] [Green Version]
- Rasool, H.; Verbrugge, B.; Zhaksylyk, A.; Tran, T.M.; El Baghdadi, M.; Geury, T.; Hegazy, O. Design Optimization and Electro-thermal Modelling of an Off-Board Charging System for Electric Bus Applications. IEEE Access 2021, 9, 84501–84519. [Google Scholar] [CrossRef]
- Verbrugge, B.; Hasan, M.M.; Rasool, H.; Geury, T.; El Baghdadi, M.; Hegazy, O. Smart Integration of Electric Buses in Cities: A Technological Review. Sustainability 2021, 13, 12189. [Google Scholar] [CrossRef]
- Rasool, A.; Yan, X.; Rasool, U.; Abbas, F.; Numan, M.; Rasool, H.; Jamil, M. Enhanced control strategies of VSG for EV charging station under a low inertia microgrid. IET Power Electron. 2020, 13, 2895–2904. [Google Scholar] [CrossRef]
- Seth, A.K.; Singh, M. Modified repetitive control design for two stage off board Electric Vehicle charger. ISA Trans. 2021. [Google Scholar] [CrossRef] [PubMed]
- Verbrugge, B.; Rasool, H.; El Baghdadi, M.; Geury, T.; Hegazy, O. Modelling and bi-level control design of a SiC off-board charging system for battery electric buses with V2G capability. In Proceedings of the 2021 23rd European Conference on Power Electronics and Applications (EPE’21 ECCE Europe), Ghent, Belgium, 6–10 September 2021; pp. 1–10. [Google Scholar]
- Chakraborty, S.; Rasool, H.; Tran, D.-D.; Geury, T.; El Baghdadi, M.; Hegazy, O. Design and Implementation of a Multifunctional 6-phase Interleaved Bidirectional DC/DC Converter for Battery Electric Vehicle Applications. In Proceedings of the 2021 23rd European Conference on Power Electronics and Applications (EPE’21 ECCE Europe), Ghent, Belgium, 6–10 September 2021; pp. 1–10. [Google Scholar]
- Selvamuthukumaran, R.; Gupta, R. Rapid prototyping of power electronics converters for photovoltaic system application using Xilinx System Generator. IET Power Electron. 2014, 7, 2269–2278. [Google Scholar] [CrossRef]
- Cherragui, H.; Hilairet, M.; Giurgea, S. Hardware-in-the-loop simulation of a boost converter with the Xilinx System Generator from Matlab/Simulink. In Proceedings of the IECON 2015—41st Annual Conference of the IEEE Industrial Electronics Society, Yokohama, Japan, 9–12 November 2015; pp. 1837–1842. [Google Scholar]
- Kumari, B.; Rana, R.S.; Patil, C.Y. FPGA and dspace based sliding mode control of boost converter for pem fuel cell application. Int. J. Comput. Appl. 2012, 51, 4–10. [Google Scholar] [CrossRef]
- Thangavelu, A.; Varghese, M.V.; Vaidyan, M.V. Novel FPGA based controller design platform for DC-DC buck converter using HDL Co-simulator and Xilinx System Generator. In Proceedings of the 2012 IEEE Symposium on Industrial Electronics and Applications, Bandung, Indonesia, 23–26 September 2012; pp. 270–274. [Google Scholar]
- Tran, D.-D.; Geury, T.; El Baghdadi, M.; Van Mierlo, J.; Hegazy, O. Design and Implementation of FPGA-based Digital Controllers for SiC Multiport Converter in Electric Vehicle Drivetrains. In Proceedings of the 2019 21st European Conference on Power Electronics and Applications (EPE’19 ECCE Europe), Genova, Italy, 3–5 September 2019. [Google Scholar]
- Battiston, A.; Miliani, E.-H.; Pierfederici, S.; Meibody-Tabar, F. Efficiency improvement of a quasi-Z-source inverter-fed permanent-magnet synchronous machine-based electric vehicle. IEEE Trans. Transp. Electrif. 2016, 2, 14–23. [Google Scholar] [CrossRef]
- Chakraborty, S.; Tran, D.-D.; Van Mierlo, J.; Hegazy, O. Generalized Small-Signal Averaged Switch Model Analysis of a WBG-based Interleaved DC/DC Buck Converter for Electric Vehicle Drivetrains. In Proceedings of the 2020 22nd European Conference on Power Electronics and Applications (EPE’20 ECCE Europe), Lyon, France, 7–11 September 2020. [Google Scholar]
- Jappe, T.K.; Polla, R.R.; Fuerback, A.L.; Heldwein, M.L.; Soeiro, T.B.; Andrich, R. An FPGA-based single-phase interleaved boost-type PFC rectifier employing GAN HEMT devices. Rev. Eletrônica Potência 2014, 19, 414–422. [Google Scholar] [CrossRef]
- Abbas, G.; Gu, J.; Farooq, U.; Abid, M.I.; Raza, A.; Asad, M.U.; Balas, V.E.; Balas, M.E. Optimized Digital Controllers for Switching-Mode DC-DC Step-Down Converter. Electronics 2018, 7, 412. [Google Scholar] [CrossRef] [Green Version]
- Rasool, H.; Zhaksylyk, A.; Chakraborty, S.; El Baghdadi, M.; Hegazy, O. Optimal Design Strategy and Electro-Thermal Modelling of a High-Power Off-Board Charger for Electric Vehicle Applications. In Proceedings of the 2020 Fifteenth International Conference on Ecological Vehicles and Renewable Energies (EVER), Monte-Carlo, Monaco, 10–12 September 2020; pp. 1–8. [Google Scholar]
- Hegazy, O.; Van Mierlo, J.; Lataire, P. Analysis, Modeling, and Implementation of a Multidevice Interleaved DC/DC Converter for Fuel Cell Hybrid Electric Vehicles. IEEE Trans. Power Electron. 2012, 27, 4445–4458. [Google Scholar] [CrossRef]
- Rasool, H.; Rasool, A.; Ikram, A.A.; Rasool, U.; Jamil, M.; Rasool, H. Compatibility of objective functions with simplex algorithm for controller tuning of HVDC system. Ing. Investig. 2019, 39, 34–43. [Google Scholar] [CrossRef] [Green Version]
- Jamil, M.; Waris, A.; Gilani, S.O.; Khawaja, B.A.; Khan, M.N.; Raza, A. Design of robust higher-order repetitive controller using phase lead compensator. IEEE Access 2020, 8, 30603–30614. [Google Scholar] [CrossRef]
- Kumar, N.; Saha, T.K.; Dey, J. Control, implementation, and analysis of a dual two-level photovoltaic inverter based on modified proportional–resonant controller. IET Renew. Power Gener. 2018, 12, 598–604. [Google Scholar] [CrossRef]
- Garcés Quílez, M.; Abdel-Monem, M.; El Baghdadi, M.; Yang, Y.; Van Mierlo, J.; Hegazy, O. Modelling, analysis and performance evaluation of power conversion unit in g2v/v2g application—A review. Energies 2018, 11, 1082. [Google Scholar] [CrossRef] [Green Version]
- Giri, A.K.; Arya, S.R.; Maurya, R.; Babu, B.C. VCO-less PLL control-based voltage-source converter for power quality improvement in distributed generation system. IET Electr. Power Appl. 2019, 13, 1114–1124. [Google Scholar] [CrossRef]
- Rasool, A.; Yan, X.; Rasool, H.; Guo, H.; Asif, M. VSG stability and coordination enhancement under emergency condition. Electronics 2018, 7, 202. [Google Scholar] [CrossRef] [Green Version]





















| Parameters | Value |
|---|---|
| Power (P, kW) | 175 |
| Line frequency (fAC, Hz) | 50 |
| Switching frequency (fsw, kHz) | 40 |
| AC voltage (VAC, V) | 400 |
| DC Voltage (Vdc, V) | 600–800 |
| Rectifier inductor (Lrect, uH) | 100 |
| Grid inductor (Lgrid, uH) | 1 |
| Capacitor (Cf, uF) | 10 |
| Damping resistance (rd, Ohm) | 0.04 |
| DC capacitor (Cdc, mF) | 0.85 |
| Controller | Generalized Transfer Function |
|---|---|
| PI | |
| Lead–Lag | , |
| Proportional Resonance | |
| Modified Proportional Resonance |
| Controller | Control Parameters | Transfer Function | GM (dB) | PM (deg) | Wcp (rad/s) | Wcg (rad/s) | ITAE | IAE |
|---|---|---|---|---|---|---|---|---|
| Id/Iq Current Control | Kp = 0.08, Ki = 520 | 33.9 | 51 | 1.73 × 103 | 3.17 × 105 | 85.95 | 19.70 | |
| PRC | 33.9 | 51 | 1.74 × 103 | 3.17 × 105 | 126.94 | 28.39 | ||
| MPRC | 33.9 | 41 | 2.2 × 103 | 3.17 × 105 | 127.78 | 28.66 | ||
| Lead–Lag | 39 | 57 | 1.61 × 103 | 3.17 × 105 | 87.23 | 19.95 | ||
| Vdc Voltage control | Kp = 0.13, Ki = 92 | 22.3 | 58 | 346 | 2.11 × 103 | 85.95 | 19.70 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rasool, H.; Verbrugge, B.; Jaman, S.; Abramushkina, E.; Geury, T.; El Baghdadi, M.; Hegazy, O. Design and Real-Time Implementation of a Control System for SiC Off-Board Chargers of Battery Electric Buses. Energies 2022, 15, 1434. https://doi.org/10.3390/en15041434
Rasool H, Verbrugge B, Jaman S, Abramushkina E, Geury T, El Baghdadi M, Hegazy O. Design and Real-Time Implementation of a Control System for SiC Off-Board Chargers of Battery Electric Buses. Energies. 2022; 15(4):1434. https://doi.org/10.3390/en15041434
Chicago/Turabian StyleRasool, Haaris, Boud Verbrugge, Shahid Jaman, Ekaterina Abramushkina, Thomas Geury, Mohamed El Baghdadi, and Omar Hegazy. 2022. "Design and Real-Time Implementation of a Control System for SiC Off-Board Chargers of Battery Electric Buses" Energies 15, no. 4: 1434. https://doi.org/10.3390/en15041434
APA StyleRasool, H., Verbrugge, B., Jaman, S., Abramushkina, E., Geury, T., El Baghdadi, M., & Hegazy, O. (2022). Design and Real-Time Implementation of a Control System for SiC Off-Board Chargers of Battery Electric Buses. Energies, 15(4), 1434. https://doi.org/10.3390/en15041434