Derivative Probes Signal Integration Techniques for High Energy Pulses Measurements

Abstract

The paper presents problems related to the processing of signals recorded with differential field probes E and H. The fundamental problem to which special attention has been paid is the result of the integration operation. Due to the presence of constant/slowly-varying components in the raw signal, there is a drift present in the outcome of integration. This line wander can be enormous. This is particularly evident if the integration is performed in a standard manner, uniformly over the entire recorded waveform. The paper contains the Authors’ proposition to segment the signal and perform the integration independently in each of the sub-regions. This approach is based on the assumption of a local mean value instead of its global character for the recorded waveform. Although this leads to more complex signal processing, it gives significantly better results as it is suppressing the deterioration drift in the integrated signal more than 400 times. The results are presented on laboratory recordings and outdoor tests. In the first case, voltage pulses with durations of about 50 ns and rise times in the range of single ns were recorded. In the second case, high-energy electromagnetic pulse signals were used. It was formed by sinusoidal waveforms packets of 3 GHz frequency with a single packet duration of 5 μs and packet repetition frequency f ≤ 300 Hz.

1. Introduction

The measurement of high-energy current pulses is performed for lightning current measurements, measurement of partial discharges, measurements of the parameters of high voltage and high current generators. These pulses are generated for electromagnetic compatibility verification and testing in order to evaluate the system or equipment shielding effectiveness and its resistance to a high electromagnetic field [1,2]. These pulses are also generated and measured in magnetic flux compression generator tests where very high current values, up to 1 MA, are used to generate electromagnetic fields capable of damaging electronic devices [3,4]. The same is for Marx generators where very fast voltage pulses ranging up to 1 MV are generated, and the energy achieved allows for electronic equipment malfunction [5,6,7]. These high value pulses can be measured with the use of transducers utilizing the optical Faraday effect [8], Ampere’s law by means of Rogowski coil and electromagnetic field probes [9].

In most cases mentioned above, both high voltage and high current measurements are performed indirectly by means of E and H field probes. This approach increases the safety of the measurement as there is a galvanic isolation of the measuring circuit and the tested circuit. On the other hand, it becomes necessary to perform additional conditioning or processing of the measurement signal. Among other popular methods used, there is the integration of measurement signals. It is performed when inductive or capacitive sensors are used to measure the field. The voltage induced at the coil terminals is directly proportional to the derivative of the magnetic field. For the capacitive sensors on the other hand, the current induced in the capacitor circuit is directly proportional to the derivative of the electric field. They require integration in both cases. The problems are presented in [10,11]. Moreover, in [12], Marconato et al. discuss the possibility of using different types of analogue and digital integrations in a circuit for the magnetic field measurement in a plasma machine. The proper selection of the integration interval plays a very important role, which was described in [13,14,15] and illustrated with an example of the Analog to Information (A2I) converter pre-integrator. On the other hand, an easy to implement algorithm using a second-order generalized integrator to control an induction motor is presented in [16].

Numerical integration brings the risk of accumulation of mean value present in the processed signal, which is manifested by the occurrence of a significant drift in the integrated output signal. The proposed methods described in the measurement instruments documentation work well in practice for periodic, stationary signals. For single pulse and in particular, floating signals, numerical integration with these methods often does not give good results.

The main goal of the work is to develop a method of numerical integration of signals which gives results comparable to analogue (hardware) integration (figures in the article). An additional goal is to develop a method not demanding computing power, so that it can be efficiently carried out directly on the oscilloscope (not always equipped with dedicated software and high computing power). For this reason, the starting point is the fundamental method of determining the mean value for the entire signal, the method commonly given in the documentation. For this method it is assumed that the mean value is constant all over the acquired signal. The Authors’ proposition is to split the signal into segments (dependent on the signal form) and independently compute local mean values applied in the following signal processing. The digital filtering tool is also not excluded from the research field. An additional reason is the fact that digital filtering can also be used to remove slow varying signal frequency components closely related to the local mean values.

Thus, in the area of electromagnetic field measurement, the need to integrate a derivative signal is quite common, but implementing the appropriate integration method for a particular measurement case is not straightforward. Our paper focuses on discussing the basic methods of integrating the signal from E and H field probes with special emphasis on regions of averaging introducing significant differences in the case of numerical integration. The paper is composed as follows:

• In the introduction, we present the most common applications required for signal integration.
• The second chapter is devoted to the presentation of theoretical background for field probes: electric field (D-dot type) and magnetic field (B-dot type) and the possible signal integration methods for these probes. The problem of signal acquisition trigger configuration is presented.
• The third chapter presents two measurement setups for different signal generators. We explain our method of signal integration and discuss the defects of using an incorrect numerical integration algorithm approach.
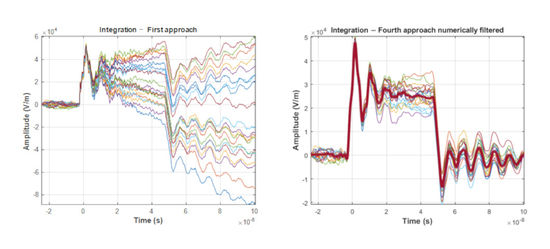
• The fourth chapter contains discussion and comparison of different approaches to the integration aspect in the measurement of electromagnetic field.
• The fifth chapter contains summary of the achieved results where the proposed integration approach gives the effective cumulative integration drift attenuation. The obtained outcomes are characterized by the drift attenuation level of a range of 400.

2. Fundamentals of Field Probes and Integration Methods

2.1. Field Probes Functional Principle

The field probes used for measurements belong to a group of transmitters for which the signal (output voltage) is proportional to the rate of change of the measured quantity, i.e., to the derivative of the measured quantity. This applies both to the electric field probe, based on a capacitive transducer, and to the magnetic field probe using an inductive transducer.

The B-dot and D-dot probes are available in two versions: single ground type for fast alternating fields at the surface, and differential free field type for fast alternating fields in space. For the B-dot ground magnetic field probe, the output signal can be written with Equation (1). The output signal for the D-dot ground probe is given by Equation (2).

$$\mathrm{U}\left(\mathrm{t}\right)=\mathrm{Aeq}\frac{\mathrm{dB}\left(\mathrm{t}\right)}{\mathrm{dt}}=\mathrm{Aeq}·{\mathsf{\mu }}_{\mathrm{o}}·\frac{\mathrm{dH}\left(\mathrm{t}\right)}{\mathrm{dt}},$$

(1)

$$\mathrm{U}\left(\mathrm{t}\right)=\mathrm{Rs}·\mathrm{Aeq}\frac{\mathrm{dD}\left(\mathrm{t}\right)}{\mathrm{dt}}=\mathrm{Rs}·\mathrm{Aeq}·{\mathsf{\epsilon }}_{\mathrm{o}}·\frac{\mathrm{dE}\left(\mathrm{t}\right)}{\mathrm{dt}},$$

(2)

where: Aeq is the equivalent area of the single sensor; B is the magnetic flux induction, H is the magnetic field strength; µ_o is the vacuum permeability. Rs is the impedance seen by a single channel of the sensor, D is electrical induction, E is electrical field strength; ε_o is vacuum permittivity.

As can be seen from Equations (1) and (2), the output signal is proportional to the physical dimensions of the probe, but most importantly it is proportional to the rate of change of the field—the derivative of the field. This forces the necessity of signal integration to obtain the value of measured field.

2.2. Signal Integration Methods

The following methods can be used to integrate the measurement signal:

• hardware (analogue) circuits;
• numerical methods.

Hardware integrators are built with RC circuits. The advantage of these integrators is the operational simplicity. This approach gives a signal directly at the output of the integrator that is proportional to the measured quantity, in this case the magnetic and electric fields. The output signal is not enormously lagged behind the raw signal before integration and can be directly recorded with an oscilloscope. This allows the operator for quick reading of the fundamental parameters of the measured field such as: its amplitude, frequency, rise and fall times or pulse length.

The condition for the correct integration of the signal is the preservation of time parameters of the signal and integrator. It should be remembered that the integration interval (0-t) should be shorter than the time constant τ = RC. This is a disadvantage of hardware methods, because the time parameters of the signal (field) being measured, must be known before the measurement. This makes it necessary to have a set of multiple integrators with different time constants ready when starting an experiment for which the frequency of the signal (field) is not known at all. The application of passive analogue integrators is relatively easy. Nevertheless, one should remember several practical aspects, which are already pointed out by the probe manufacturers themselves [17]. First, the integrator should be connected directly to the oscilloscope’s input without any additional connecting cables. This is shown in Figure 1c (recommended connection). Laying the lead wires, one should remember to avoid, as far as possible, any bends in the cable. Manufacturers of probes do not recommend using e.g., angled BNC connections. It is also probably dictated by the fact that in the case of bent connections it is difficult to maintain constant geometry of the circuit and consequently impedance parameters. It is especially important at high frequencies. It should also be kept in mind that correct integration results are easier to be obtained when the entire measurement path is at a common ground reference potential. Therefore, a semi-rigid cable is commonly used in this type of measurements. However, it is not recommended to use passive analogue integrators in a measurement system with the optolink connections. This is mainly due to the low voltage range of the optoelectronic circuit and noticeable noise deteriorating the measurement signal. In this case, one should use numerical integration directly in the oscilloscope or perform that stage in the post-processing activity.

Numerical integration is the approximate calculation of definite integrals [18]. The methods approximate the integral by using the sum of the values of the function being integrated at several points. To obtain a more accurate approximation, the integration interval is divided into small fragments. The final result is the sum of the estimates of the integrals in each subinterval.

For the numerical integration of signals, the rectangle or trapezoid method can be used, but the latter is more accurate and popular.

In the trapezoid method, the approximation improves because one approximates each of the sub compartments linearly, which can be written as follows (3):

$${{\displaystyle \int }}_{\mathrm{t}0}^{\mathrm{tn}}\mathrm{u}\left(\mathrm{t}\right)\mathrm{dt}\approx \frac{\mathrm{h}}{2}{{\displaystyle \sum }}_{\mathrm{i}=0}^{\mathrm{n}-1}\left(\mathrm{u}\left({\mathrm{t}}_{\mathrm{i}}\right)+\mathrm{u}\left({\mathrm{t}}_{\mathrm{i}+1}\right)\right),$$

(3)

where n is the number of subintervals of length h.

The use of simple numerical methods is caused by the fact that in case of high sampling frequency of the signal (this is usually the case), the error of integration is relatively small (very narrow subintervals of integration). This gives the possibility of carrying out the integration process directly on oscilloscopes recording the waveforms from measurement equipment. The trapezoid method, though it can be considered basic (as compared for example to Simpson method), is commonly used as an integration formula in oscilloscopes.

Numerical post-processing provides the most tools, methods and opportunities that can be applied (if only necessary) into the integration process. In this case, the signal recorded on the oscilloscope is processed using signal processing dedicated software and powerful computers, after the completion of measurement experiments. A relatively long delay in obtaining results is a disadvantage of this procedure, but the certainty of the process correctness as well as the possibility of performing additional analysis, e.g., spectral or wavelet analysis and additional filtering often compensates for the mentioned disadvantage.

2.3. Practical Problems of the Signal Acquisition

By definition, the output signals of B-dot and D-dot probes do not contain a constant component. However, this component may appear in the conditioned measurement signal immediately before the functional integrator block. There may be several reasons for this condition. First of all, it can happen as a result of imbalance of the measurement path. Another reason may be the accumulation of electrostatic charges, especially in high-impedance lines (leads of the Programmable Gain Instrumentation Amplifier). In practice, however, a lot depends also on the selection of the oscilloscope recording time (period). Documentation dedicated to measurement instruments commonly gives the integration of a periodic, rectangular signal generated by oscilloscope built-in test generator as an example. In this case, as the signal occupies the entire recording period (window), and especially when the screen presents the whole number of signal periods (with significant amplitude), removing the DC component is an uncomplicated task (Figure 2). In manual mode (convenient for demonstration but impractical especially for a series of measurements), the average value is found using the oscilloscope knobs.

To automate the measurement, it is more convenient to determine the mean value using a dedicated function and subtract it from the samples of the recorded signal before integration. This technique works well for periodic and single shot signals under certain conditions.

For the single pulse signals, it is important to select the recording length as to record the entire phenomenon, possibly without an excessive “zero” space following the occurrence of the phenomenon. In each case, the trigger point is commonly set between the first and second oscilloscope display division of the time base (typical setting). For such a setting, the mean value before the trigger point (pre-trigger zone) for the background signal (zero would be ideal) can be determined. Depending on the approach, the mean value in the post-trigger region where the raw (not yet integrated) measurement signal (recorded phenomenon) is located, can be determined separately. This variant is especially helpful in cases where it is difficult to match the length of the registration window. Moreover, in the case when, apart from the constant component, there are slowly varying components in the signal, high-pass filtering, preceded by a spectral analysis of the signal, it turns out to be useful or even demanded.

3. Experiments Explanation and Results Discussion

3.1. Measurement Setup for Nanosecond Pulse

Experiments were performed in two independent configurations. The starting point was the laboratory configuration presented in the Figure 3, with the measurement of voltage and electric field in the neighborhood of the wire (plate-wire configuration) supplied by the kilovolts/nanoseconds pulse generator.

The results of various laboratory integration configurations will be presented in the example of measurement in the plate-wire system, used to estimate the voltage based on the value of the electric field. The measurement system consisted of three independent measurement paths. The first one was a voltage probe, the second was an electric field probe with analogue integration—a hardware, capacitive integrator and the third was an electric field probe identical to the second, but in this case the integration was performed numerically (Figure 4).

Figure 5 presents the results of a series of measurements of a system powered by a pulse generator in the same manner as depicted above. The exemplary pulse was 2 kV amplitude of a 50 ns duration.

In Figure 5, one can see the high repeatability and stability of the signal pulses when measured with voltage probe and ground plane field probe with hardware integration (Figure 5a,b). Unfortunately, it cannot be observed (and consequently confirmed) in the numerical integration case (Figure 5c). It is due the high sensitivity of the numerical integration to the presence of a DC and very low frequency components in the input signal. At first, in the case of numerical integration, the average value required for the proper integration process was determined for the entire recording window (range marked in red). The effect of accumulation of constant values can be seen already in the initial phase of recording, before the actual triggering (t < 0), which results in the appearance, instead of a zero signal, of rising or falling waveforms. As a result, the voltage impulse itself, when analyzing the measurement series, is characterized by a very large dispersion. Interpretation of the results in this case is difficult and leads to significant, unacceptable results. For this reason, a number of experiments were carried out to eliminate the above-mentioned undesirable effects. The first experiment assumed, as in the case of numerical integration carried out on an oscilloscope, that the constant component does not change in the recording window. This time, however, the value was determined and subtracted from the raw input only on the basis of the recorded background signal before the triggering of the measurement system (t < 0)—Figure 6.

The nature of the results of the first approach should be considered experimental (Figure 6). Although an improvement (signal stabilization) was achieved in the pre-trigger region, the final effect is much worse than in the case of the standard approach. This is mainly revealed in the enormous dispersion of the measurement series signals in the most important area, i.e., in the interval containing the measurement signal. Therefore, it was decided to modify the calculations so that the mean value determined in the pre-trigger interval was subtracted from the entire recorded signal (Figure 7).

As one can see in the second approach, the obtained results are better than in the first approach, but still much worse than the standard approach (Figure 5c). Nevertheless, the results obtained in the first and second approaches, related to the standard calculations, lead to the conclusion that the assumption that the constant component does not change in the recording window cannot be taken for granted. Therefore, subsequent experiments were carried out, fragmenting the recorded waveforms, determining the intervals in which only the background is visible and those in which the measurement signal was recorded.

Thus, in the third approach, mean values were determined in three intervals. Before the signal, during the signal–square pulse and after the signal. These values were subtracted independently in the respective regions. The results are shown in Figure 8, distinguishing the regions for which local mean values were determined and then used in the calculations. As can be observed, the assumption of local mean values significantly improved the obtained results. As before, the pre-trigger region does not show any trends. However, most importantly, the range in which the signal itself is located also does not show signs of rising or falling trends. It is also worth noting that the record fragments containing rising and falling edges obtained in this approach are characterized by a high repeatability in the series as compared one to another.

Comparing the results obtained in the third approach to the signal acquired with an analogue integrator, they are characterized by an even greater dispersion in the series. This is primarily due to the frequency properties of the analogue integrator and the raw numerical integration operation. This phenomenon can be minimized by averaging the results from a series of measurements, or by performing low-pass digital filtering (based on analysis of the signal spectrum), or by combining both techniques.

In order to meet the conditions of the experiment, another (fourth) approach of calculating the mean value was carried out. This time the mean value was calculated separately in pre-triggering and post-triggering intervals (Figure 9). The purpose of this test was to check how the introduction of computational simplifications would affect the final results. Though it represents much better performance compared to the first two cases, as it could be expected, the results obtained here are worse than in the third approach. The difference is especially visible in the intervals containing the rising and falling phases of the rectangular pulses. In all cases, the integration was also performed in the regions following the measurement signal. First of all, this activity made it possible to locate the end of the phenomenon, observe transients, and finally, possibly, detect wave phenomena. Summing up, the best results were achieved for the mean values calculated separately before, during and after the observed signal. Additionally in this case, the numerical low-pass filtration was carried out and the series of measurements were additionally averaged. Digital low-pass filtration parameters were selected upon the frequency spectrum of the measured square pulse signal (Figure 10) in order not to disturb the essential pulse properties. Duration of the observed pulses ranges within 50–55 ns. For this application, the low-pass filter cut off frequency was set to 400 MHz, which encompasses both a fundamental and significant number of harmonics. The obtained outcomes are presented in the Figure 11. Finally, a result very similar to the case with analogue integration was obtained. Therefore, a question can be asked about the advisability of all the above-mentioned measures. The answer is not complicated.

The conducted experiments were carried out in conditions of relatively low electric field values and in a system in which the lead wires were not longer than 1 m, and the probes themselves were connected to the ground of the system.

These conditions may not always be met. In general, measurements may be performed for very large field exposure values with the requirement of the spatial distribution to be determined. In such a case, the probes will not have a galvanic reference point (ground), the recording devices will be located in special shielding boxes at a great distance from the signal source. The consequence of the last two conditions is the necessity to use optical links, ensuring galvanic isolation but also significantly limiting the range of operating voltages of the measurement setup. Under such conditions, the use of passive analogue integrators is limited.

3.2. Measurement Setup and Procedure for High Power Microwave—HPM Generator

The second, outdoor setup involved signal emitted from the HPM generator which has the form of a set of packets (pulse/sinus train) of a sinusoidal waveform with a frequency of 3 GHz. The duration of a single packet was approximately 5 μs and the repetition rate of the packets was adjustable up to 300 Hz. The total duration of one emission cycle was expressed in individual seconds. The measurement system setup is shown in Figure 12.

Field measurements with the HPM generator were made at distances of 10, 20 and 30 m from the signal source (parabolic antenna). Each time a set of a dozen or so sinusoidal packets was registered and the first of them was rejected due to its unspecified nature, which stems from the properties of the generator itself (Figure 13).

The recording of fast-changing bursts of pulses repeated with a relatively low repetition frequency (GHz/kHz) requires an appropriate configuration of the recording device (oscilloscope), but thankfully it is typically available in devices operating in the Gigahertz bands.

Based on the acquired signal (Figure 13), initial integration was performed, but it was seriously disturbed. Integration of sinusoidal packets should result in sinusoidal wave form as well. Such an expectation cannot be found in the Figure 13.

Despite the differential nature of the probes used, the recorded signal showed noticeable low-frequency components (up to 2 MHz in Figure 14), which were the source of significant errors in the integration operation (Figure 13b). Thus, the traditional integration stage was additionally supplemented by high-pass filtering, with the cut-off frequency determined on the basis of the observed signal spectrum. The cut-off frequency of the filter was set to encompass the slow varying signal components—2 MHz region on Figure 14. Sample results are shown in Figure 15.

Although the electric field was the fundamental measurement parameter, it was also decided to register the magnetic field in the presented measurement system. This was primarily due to the intention to obtain as much information on the recorded phenomenon as possible. Independently, the reconstruction, re-alignment and configuration of the source and measurement object in the presented case is very complex and complicated. In practice, it becomes a one-time measurement observation opportunity. Registration of electric and magnetic fields allows for additional verification of correctness of the results by computation of the impedance of the medium, which in ideal conditions is 120π Ω. Based on the registration of fields in the presented system (Figure 16), the determined value of the medium impedance is 467 Ω +/− 26%, which is a satisfactory result because only the catalogue data of the measurement system component were taken into account when estimating the error, neglecting the imperfection of the geometric configuration of the measurement system.

Issues related to signal processing (integration operation) have the same course irrespective of whether they concern registration of electric or magnetic field. Therefore, the paper presents this issue only on the example of an electric field (most valuable parameter in the measurements performed).

4. Discussion and Comparison of Results

The necessary integration of the differential probes signal can be carried out in many ways. Hardware/analogue integrators give the possibility of direct integration, but their use is justified in a case where the signal frequency band is known or the measured signals have a relatively high amplitude and are grounded. However, these requirements cannot always be met. This is especially difficult in the case of spatial measurements (floating signals) and additionally high-energy EM fields. For safety reasons, the distances between the measurement point and the measurement instrumentation location are large. In such cases, fiber optic links are commonly used. Their basic feature, which is often a requirement, is galvanic insulation of the signal connection. However, these links limit the amplitude of the transmitted signals. In such systems (floating and low-amplitude signals), numerical integration is commonly used. A list of the different signal integration techniques is presented in

Table 1. Integration methods comparison.

Integration Type	Method	Common Signal Parameter: Signal Rise Time	Requirements, Measurement Conditions	REF
Hardware	Passive integrator 1 μs or 5 μs	Magnetically insulated transmission line (MITL). trise = 96 ns	Directly in the transmission line, galvanic connection	[19]
Hardware	Self-integration probe selected frequency band.	Lightning current trise = 8 μs	Known signal parameters, unchanged measurement setup configuration, galvanic connection	[20]
Numerical	Mean value removal	Calibration testing signal trise = 4.2 ns	unchanged measurement setup configuration, galvanic connection	[21]
Numerical	FIR filter	High-power microwave (HPM) pulses trise = 3 ns	Self-developed measurement instrument	[22]
Numerical	FFT and FIR filter	HV pulses measured in the close neighborhood of the cable trise ≤ 1 ns	Short connections, signal processing in Matlab	[23]
Numerical	Local Mean value (segmented signal) removal with an optional FFT and FIR filter	HV pulses, HPM pulses, trise ≤ 5 ns	Floating signals, spatial, outdoor measurement. Numeric operation computed directly on oscilloscope	Current work

.

In the work [19], passive RC integrators were used to integrate the signal from B-dot probes installed in the magnetically insulated transmission line—MITL. The authors get good results, but it should be noted that the probe is installed directly in the MITL line, where one is dealing with the reduction of interferences. In addition, the spatial configuration of the measurement system is constant and does not change during the measurements.

Yako at al. in the work [20] present the B-dot probe with internal integration (self-integration) obtained by the appropriate selection of the parameters of the measurement circuit. The system is tested with standard 8–20 μs pulses with a current amplitude ranging from 5 kA to 37 kA. As in the work [19], the spatial configuration of the system is constant, and the measurement circuit has a short signal path. In addition, the frequency parameters of the signal are known. The paper [21] presents the process of laboratory calibration of B-dot probes with pulses of a rise time from 4 to 400 ns. Integration is carried out numerically. Due to the stable parameters of the generated pulses, the standard method of eliminating the constant component (signal mean value) was used. The use of numerical integration and the elimination of the average value by means of low-pass FIR filters are presented in [22]. The authors carry out measurements with D-dot probes. Conditioning and signal processing is carried out using a dedicated (developed) measurement instrument instead of the oscilloscope.

In turn, Huiscamp et al. [23] present a method of measurement of very fast voltage pulses (t_rise < 1 ns) with amplitudes up to 14 kV with D-dot probes mounted directly on the coaxial cable, with which the pulse is transmitted. The Authors propose to record the signal using an oscilloscope and then post-process it based on FFT analysis, elimination of the mean value component, taking into calculations the parameters of the transmission path and finally numerical integration. Signal processing is performed in the Matlab environment.

The method proposed in this article is supposed to be effective and require relatively simple numerical operations, although more complex operations such as FFT and filtration are not excluded. Compared to the methods listed above, the approach presented in the article is characterized by independent determination and elimination of the local mean values in signal segments. Its simplicity also makes it possible to be implemented directly on the oscilloscope. The measurement signal may contain variable frequency parameters and an average value that varies along the acquisition. Sensing of the EM field in space excludes the galvanic connection to the ground, which is guaranteed by the optical link. The spatial configuration of the measurement system can vary and the distance between the measurement instrument-oscilloscope location and the measurement probes does not matter.

The above features make it possible to use the method in the outdoor EM field measurements. In addition, the reliable value of the measured EM field is obtained right after registration, which in the case of EM field tests is often more important than a low measurement error.

5. Conclusions and Summary

Based on the waveforms recorded in the measurement grounded circuits, high repeatability of the waveforms can be observed (Figure 5a,b). The effectiveness of the proposed and used integration methods can be evidenced by the measure of the scatter of values, containing the residual “constants” after integration. Based on Figure 5a,b, it is reasonable to conclude that the recorded waveform in the final phase has zero value. However, in the first approach to the implementation of integration (Figure 6), it can be observed that this is not the case at all. The scatter of the final values in this case varies from −83 kV/m to 60 kV/m, i.e., the rate of changes is at the level of 143 kV/m. In the second approach (Figure 7), the respective value is noticeably smaller, but still 104 kV/m. In the third and fourth approaches (Figure 8 and Figure 9), where the integration was performed segmented, these values are mutually comparable and reach only 0.3 kV/m, which proves high effectiveness of the applied modifications. The elimination of the trend in the integrated waveforms significantly facilitates or even enables a correct reading of the field parameters after integration.

The presented problem is common as measurement signals are acquired with the use of derivative nature probes. It extends the instrument (oscilloscope) user manuals procedure for which signal is being integrated and contains the DC component that is not varying along the acquisition buffer (window). In the practical conditioning procedure, it was assumed that the mean value of the signal was a variable along time in the recorded signal window. Based on that, the acquisition window was divided into pre and post trigger regions along with the signal and background noise content periods. Additionally, the measured signals frequency parameters were also taken into the account allowing for a proper selection of frequency of numerical filtration parameters. The latter technique promises to be a useful procedure in the integration computation. The presented HPM pulse examples, due to the nature of the measured signal, were not a demanding task and allowed for the elimination of slow-varying components (up to 5 MHz band). The filtration process is not constrained to such signals and can be applied in general as an integration technique. Each time, it should be adapted to the signals being measured, of course, so that it does not disturb the information of the observed phenomenon. Finally, as a result presented in the paper, it was possible to effectively determine the waveforms describing the changes in the electric and magnetic fields using the numerical integration operation. Removal of DC and additionally low-frequency components from the input raw signal, made it possible to avoid the accumulation of non-zero average values of the integrated waveform, which in turn gives the effect of saturation after integration.

Signal processing preceding the essential integration procedure assumes that it is performed under given conditions. First, the DC band components are not varying in time along the acquisition window (oscilloscope recording) and are relatively easy to investigate. In practice, it does not have to be fulfilled, thus instead of a precise mean value component one gets only an estimation. This, in turn, deteriorates the final results. The idea of mean values computed independently in different sub-periods of the acquisition window is also quite simple in terms of computational power requirements. On the other hand, the application of different procedures can significantly decrease the distortion of the measurement signal. Surely it can be a starting point to the automatic or at least semi-automatic processing procedure.