Next Article in Journal
Automatic Evaluation of an Interwell-Connected Pattern for Fractured-Vuggy Reservoirs Based on Static and Dynamic Analysis
Previous Article in Journal
Impact of Digital Economy on Energy Supply Chain Efficiency: Evidence from Chinese Energy Enterprises
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Energies
Volume 16
Issue 1
10.3390/en16010570
energies-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Effects of the Aspect Ratio and Cross-Sectional Area of Rectangular Tubes on Packing Characteristics of Mono-Sized Pebble Beds

by
Baoping Gong
1,*,
Hao Cheng
1,
Juemin Yan
1,
Long Wang
1,
Yongjin Feng
1,2 and
Xiaoyu Wang
1
1
Southwestern Institute of Physics, P.O. Box 432, Chengdu 610041, China
2
Nuclear Power Institute of China, P.O. Box 436, Chengdu 610041, China
*
Author to whom correspondence should be addressed.
Energies 2023, 16(1), 570; https://doi.org/10.3390/en16010570
Submission received: 21 November 2022 / Revised: 22 December 2022 / Accepted: 26 December 2022 / Published: 3 January 2023
(This article belongs to the Section B4: Nuclear Energy)
Browse Figures
Versions Notes

Abstract

:
The packing characteristics of a pebble bed are essential to understand the heat- and mass-transfer processes occurring within a granular system. Therefore, the packing characteristics of rectangular prismatic pebble beds randomly packed with mono-sized pebbles are analyzed. In terms of the average and local packing fraction distribution, coordination number, and radial distribution function, the effects of the rectangular tube aspect ratio and cross-sectional area on the packing properties of pebble beds are explored in depth. The findings indicate that the packing structures of the rectangular pebble bed exhibit noticeable fixed-wall effects. The average packing fraction and coordination number gradually decline as the rectangular tube aspect ratio rises. Close to the fixed wall, a noticeable wall effect can be seen in the distribution of axial and local packing fractions and the pebble center distribution. The wall effect has an increasing effect on the axial and local packing fraction distributions in rectangular tubes with increasing aspect ratios. Additionally, the average packing fraction and the average coordination number also increase as the cross-sectional area increases, indicating a gradual weakening of the wall effect as the cross-sectional area increases. Furthermore, the cross-sectional area and aspect ratio of the rectangular tubes affect the RDF values of the rectangular pebble beds but have no impact on the RDF features. The findings reported in this paper will be helpful for designing and optimizing pebble beds in the breeding blanket of fusion reactors.

Graphical Abstract

1. Introduction

Granular packings are common in natural and industrial systems. For instance, in the chemical industry, the catalytic reaction bed is always formed by the packing of spherical or other nonspherical catalytic pellets [1]. In nuclear energy systems, the core system of a high-temperature gas-cooled reactor is a cylindrical pebble-bed assembly packed with spherical fuel particles [2,3,4]. For a fusion energy reactor, the tritium breeder and neutron multiplier pebbles are packed in rectangular [5], U-shaped [6,7,8], or cylindrical vessels in blanket modules [9,10,11]. In addition, pebble packings are also widely used in some other fields, such as 3D-printing processes [12], pellet sandpiles [13], the packing and combustion processes of biomass fuel particles [14], storage of grain particles [15], solar energy storage systems [16], etc. Generally, most applications are often presented as dense-packed or fluidized beds. The packing characteristics, such as the packing fraction (γ), porosity (ε), coordination number (CN), and radial distribution function (RDF), have a significant influence on their applications due to the heat- and mass-transfer processes [17,18,19,20,21,22,23] and thermomechanical behaviors [24,25,26,27] of the pebble beds, which are closely related to the packing characteristics. Therefore, a comprehensive understanding of the packing characteristics in pebble beds plays a vital role in analyzing pebble beds’ heat- and mass-transfer processes and promotes a broader application of packed pebble beds.
The packing characteristics of randomly packed pebble beds are influenced by many factors, such as container dimension and shape, pebble size distribution, and packing mode [28,29,30,31,32,33,34,35,36,37,38]. Since most pebble beds are confined by a cylindrical wall in many applications, the packing structures of cylindrical beds have been widely investigated [17,18,19,23]. Several empirical prediction models of the average and radial porosity distribution were reviewed by Antwerpen et al. [28] and Seckendorff et al. [29]. In addition, the pebble packing in containers with other shapes, such as annular [25,38,39,40,41,42] and square and rectangular columns [31,43,44,45,46,47,48], were also used in the nuclear energy system. For instance, Reimann et al. [35,42] explored the packing characteristics of cylindrical, annular, and prismatic pebble beds packed with unary pebbles. The results showed that regular packings and radial porosity oscillations also exist close to the fixed inner wall. Wang et al. [11,38,41] analyzed the packing structures and mechanical properties of annular pebble beds in fusion blankets. The friction coefficient and restitution coefficient affect the static packing characteristics of polydisperse pebble beds. Du Toit et al. [39] and Ren et al. [40] explored the variations in radial porosity distribution in annular pebble beds in high-temperature gas-cooled reactors. Along the radial direction, the porosity distribution also showed oscillations and damping characteristics close to the lateral walls.
Pebble packing in differently shaped channels and tubes has recently been given more attention, particularly for microchannel reactors and nuclear fusion blankets. The pebble-packing structures in cubic or square containers are investigated by packing experiments and numerical modeling. Desu et al. [45] analyzed pebble packing in a square prismatic container and explored the effect of various filling strategies on the packing fraction. The results show that the extent of the wall effect on the packing structures is also affected by filling strategies, such as vibration, compression, and confined top walls. Hamzah et al. [46] and Beavers et al. [44] explored the porosity variation and flow behavior in square pebble beds. Several equations were also proposed to predict the local porosity distributions in three defined zones in a square pebble bed. Gong et al. [7,8,32] and Taguchi et al. [48] investigated the packing fraction and the local porosity distribution in cylindrical and cubic pebble beds. A similar porosity distribution was obtained in a cubic pebble bed. Zobel et al. [49] explored the effects of a cylindrical wall with hexagonal hemispheres on the lateral and radial void fraction distribution. The structured wall of hexagonal hemispheres can reduce the oscillation of porosity caused by the wall effect. Furthermore, for pebble packings in rectangular containers, Buchlin et al. [43] and Reimann et al. [34] investigated the void fraction distribution of randomly packed pebble beds in a rectangular container by an experimental technique based on a photoelectric process and 3D tomography. Jaggannagari et al. [50] also investigated the effects of vibration-induced crystallization and pebble-size polydispersity on the packing structures in a slender prismatic container by comparing their results with the experimental results in Ref. [34]. The results show that the crystallization initially starts at the wall. The vibration-induced crystallization increases the packing density in the fixed pebble bed. Wang et al. [47] studied the packing structures of pebbles in several rectangular containers with fixed long edges and variable widths. The results show that the bed dimension notably influences the packing structures of the rectangular pebble beds. Oguz et al. [51] and Pistocchini et al. [52] explored the packing structures of spheres confined between two narrow parallel walls.
The abovementioned investigations revealed that the container shape tremendously influences the packing structures of a packed pebble bed, especially for a small-size pebble bed. Recently, pebble beds in square and rectangular containers have been adopted for microchannel catalytic reactors used in the chemical industry and tritium breeding blankets in nuclear fusion reactors. Although the packing structures and transport process in cylinder pebble beds have been widely explored, studies on square and rectangular beds are still limited. For example, the effects of the aspect ratios of rectangular channels and the cross-sectional areas of the rectangular tube on pebble packing in rectangular containers are still seldom studied. The inner structures of the rectangular beds are rarely systematically analyzed. Therefore, this study aims to systematically analyze the effect of the aspect ratio and the cross-sectional area of the rectangular tube on packing structures for mono-sized pebble-packed beds, focusing on the average and local packing fraction, coordination number distribution, and radial distribution function. The results described in this work will provide a reference for the design optimization of the tritium breeder blanket in nuclear fusion reactors and the analysis of heat and mass transfer in the microchannel pebble reactor.

2. Methodology

In this work, the mono-sized pebbles were packed randomly under gravity without using other densification techniques, such as vibration, knocking, tapping, and so forth. Recently square-channel- or rectangular-duct-packed bed are often found in microchannel catalytic reactors and nuclear fusion blankets [53,54]. Therefore, the mono-sized pebble-packing structures were investigated with emphasis on the effect of the rectangular tube aspect ratio and cross-sectional areas in this study. The detailed methods of the packing experiments and the discrete element method (DEM) simulation can be seen in Section 2.1 and Section 2.2.

2.1. Packing Experiments

In packing experiments, the average packing fraction (γavg) of the pebble beds can be more easily obtained by the weighing method. In contrast, the inner packing structure of the pebble bed is more difficult to obtain. However, the inner packing structures of pebble beds can be easily obtained from DEM modeling. Therefore, in this study, the DEM simulation was validated firstly by comparing it with the γavg of a square pebble bed obtained experimentally. Then, the DEM was further used to simulate the pebble packing in rectangular tubes and analyze the packing characteristics of the rectangular pebble beds with different aspect ratios and cross-sectional areas.
The filling processes under gravity were selected in the packing experiments and the DEM simulations, as shown in Figure 1. Packing experiments were performed by filling pebbles into the square tubes. The γavg of the rectangular pebble beds was measured by the weighing method. The relationship between packing fraction (γ) and porosity (ε) is as follows: γ + ε = 1. In packing experiments, square tubes made of plexiglass with an aspect ratio α = 1 were selected for validation with DEM simulations. The edge length of the square container varied in the range of 10–40 mm. The pebble diameters were 1 mm. In addition, the heights were not less than 60 mm to reduce the impact of the pebble bed’s height effect (or thickness effect). The main filling processes are as follows:
  • Step 1: The volume Vc inside a rectangular container was measured by measuring the inner dimension of the rectangular tube with a vernier caliper or gauging by the drainage method and the mass mr of the rectangular container;
  • Step 2: The pebbles with density ρ and diameter d are filled into the rectangular tube from the top opening of the container under gravity in batches. After filling the tube, the pebbles above the container height are scraped off with a steel ruler;
  • Step 3: By subtracting the mass mr of the tube container from the total mass mall of the pebble bed filled with pebbles, the total mass mbed of the pebbles inside the container was obtained, mbed = mall − mr;
  • Step 4: The total volume ∑Vp of pebbles packed in bed can be calculated using the density ρ and the total mass mbed, ∑Vp = mbed/ρ. The volume ratio of the sum volume ∑Vp of pebbles in the rectangular tube to the volume Vbed of the bed is the average packing fraction γavg of the pebble bed γavg = ∑Vp/Vbed.

2.2. Simulation Method and Parameters

The discrete element method (DEM), proposed by Cundall and Strack [55], is currently widely used. For example, DEM models were adopted in the debris bed formation simulations of the pressurized water reactor [56,57], the fluid–structure coupling behavior of multiphase flow in accelerator-driven system [58,59], and the helium flow behavior in the spherical bed of a fusion reactor [60]. Thus, the DEM model was employed in this work to simulate the pebble-packing process. In the DEM simulations, a lot of helpful information, such as pebble center coordination, velocity, contact force, and so on, can be obtained, some of which are arduous to measure in packing experiments. In the DEM simulation, the pebbles are assumed to be hard spheres. The motion of the pebbles is calculated based on Newton’s Second Law of Motion. When the distance between two pebble centers is smaller than the sum of the radii touch distance (Ri + Rj), the contact force and the friction action are evaluated based on the Hertz–Mindlin [61,62] theory and Coulomb friction criterion. The detailed theory of DEM can be found in the literature [7,8,55,62].
In this study, LIGGGHTS-PUBLIC [61] was employed. The pebble parameters used in this study are listed in Table 1 by referring to the parameters of the Li4SiO4 ceramic pebbles in the literature [7,8,11,31]. The heights of all pebble beds are higher than 60 mm. The aspect ratios of the pebble beds vary from 1 to 10. When the aspect ratio is equal to 1, the container is square. When the cross-sectional area of the rectangular container is fixed, as the aspect ratio increases, the longer edge length increases, and the shorter edge length simultaneously decreases. The exact bed sizes are listed in Table 2.
During the simulation of pebble packings, the pebbles were filled into the cavity under gravity in batches. The detailed packing processes in the DEM simulation are as follows:
  • Step 1: In the top-opening region, which is higher than 60 mm, a certain number of spherical pebbles with a diameter of 1 mm are randomly and uniformly generated without overlaps;
  • Step 2: The randomly generated pebbles fall to the bottom of the cavity with an initial velocity of zero under gravity. Meanwhile, a variable number of pebbles will be randomly regenerated in batches at every fixed timestep. Moreover, they continue to move down freely and slowly with an initial zero velocity. During the pebble packing, the total pebble number and the pebble-bed height in the container will gradually increase. The kinetic energy of the inserted pebbles is gradually dissipated by the friction, rolling, sliding, and collision between pebbles. The pebble-packing process can be monitored by the total kinetic energy of the granular assembly;
  • Step 3: When the pebble-bed height exceeds 60 mm, the filling process is stopped. With the gradual dissipation of energy, the pebble bed can be stable when the total kinetic energy is reduced to ~10−14 J [7]. Then, the pebbles higher than 60 mm are removed. The simulation continues to make the pebbles reach a stabilized packing state until the total kinetic energy is reduced to ~10−14 J again;
  • Step 4: When the stabilized state of pebble packing is achieved, the packing characteristics of the rectangular pebble bed will be analyzed by the in-house Matlab codes.

2.3. Calculation of the Packing Fraction

The packing fraction is an important property that describes the densification degree of a pebble bed. In this study, the average packing fraction, the axial packing fraction, and the local packing fraction were calculated by referencing the literature [30]. The average packing fraction γavg is defined as the volume ratio of all pebbles packed in the pebble bed to the volume of the container that the pebbles occupied γavg = (∑Vp)/Vbed, where Vp is the pebble volume and Vbed is the pebble-bed volume. The γavg is a volume-averaged parameter. In the packing experiments, the ∑Vp was determined by the pebbles’ weight and density. In DEM simulations, Vp was calculated by the diameters and total numbers of the pebbles packed in the rectangular tube. The axial packing fraction γaxi is an area-averaged parameter. The pebble bed is divided into numerous parallel-cut planes along the direction perpendicular to the fixed walls from one fixed wall to another parallel fixed wall, with distance steps of 0.05 d. The γaxi is defined as the area ratio of the summed intersection areas between the pebbles and cut plane to the area of the cut plane. Thus, the γaxi can be expressed as γaxi(x) = (∑Scut)/Splane, where Scut is the intersection area between a pebble and the cut plane at the position x. Splane is the area of the cut plane at position x. The local packing fraction γlocal is a line-averaged parameter that reveals the local distribution of the packing fraction in a pebble bed. The γlocal is calculated by the ratio of the summation of all intersection line segments to the length of the grid line. The detailed calculation method can be seen in [30].

3. Results and Discussions

3.1. Validation with Experiment Results

The DEM results of the pebble packings in square tubes (α = 1, Lx= Ly) were validated by comparing them with the experimental results in terms of the γavg. All pebble-packing experiments were repeated three times to validate the repeatability of the experiment. The detailed experiment results, mean value, and standard deviation are listed in Table 3. The results show that the γavg of the packed pebble beds in square tubes gradually increases with the scale ratios, Lx(=Ly)/d. When the Lx/d ≈ 10, the γavg is only about 0.59. When the ratio of Lx/d is larger than 15, an γavg > 0.60 can be easily obtained. When increasing the ratio to Lx/d ≥ 25, the γavg can be larger than 0.62. The DEM results agree with the experimental results for the packed square pebble beds, as shown in Figure 2. Thus, for the pebbles packed in rectangular tubes, the DEM was adopted to obtain the detailed internal packing structures of the rectangular pebble beds.

3.2. Average Packing Fraction

The final stable packed pebble beds in rectangular tubes with various aspect ratios of 1~10 and a fixed cross-sectional area of 225 d2 are shown in Figure 3. The 3D views of the rectangular pebble beds with the different cross-sectional areas of 100 d2–1600 d2 and a fixed aspect ratio of 5 are shown in Figure 4. The γavg of the rectangular pebble beds is shown in Figure 5.
Figure 5a shows that the γavg of the pebble beds gradually decreases with the increase in the aspect ratio α of the rectangular tubes. However, the reduction rate of the γavg in the pebble beds with various cross-sectional areas is different. When the rectangular tube has a relatively large cross-sectional area, such as larger than 225 d2, the γavg decreases linearly with the increase in the aspect ratio α. The reduction rate decreases with the increase in the cross-sectional area. However, when the rectangular tube has a smaller cross-sectional area, the γavg exhibits large oscillations and scattering. For instance, when the cross-sectional area = 100 d2, an increase in γavg occurs when the aspect ratio α is in the range of 6–8, mainly due to the regular arrangement of pebbles in the small and narrow rectangular tubes under the influence of the fixed wall. When the aspect ratio α > 6, the smallest side length of the rectangular tube cross-section is already smaller than 4 d (see Table 3). When the aspect ratio α > 8, the γavg gradually reduces and the smallest side length also reduces to <3.5. The oscillations and scattering can also be observed in the literature [52] for the narrow pebble bed. This is because, at this time, the pebbles are regularly packed with various fractions of cubic and hexagonal packing. The γavg of the pebble bed is closely related to the ratio of the smallest side length to the pebble diameter. A small change in the smallest side length will result in a considerable variation in the γavg of the pebble bed owing to the fixed-wall effect and hybrid regular packing.
In addition, Figure 5b shows the variation in the γavg with the cross-sectional area. The results demonstrate that with the increase in the cross-sectional area of the rectangular tubes, the γavg of the pebble beds with different aspect ratios gradually increases, and the scattering of packing fraction gradually weakens for pebble beds with different aspect ratios. This proves that the rectangular tube dimensions influence the packing characteristics of the pebble bed. Nevertheless, as the bed scale increases, this effect gradually diminishes.
To clearly show the effect of the rectangular tube dimension on the packing structure, the γavg of the pebble beds with various aspect ratios and cross-sectional areas are shown in Figure 6. The Lx and Ly were normalized by the pebble diameter. Note that the side lengths Lx and Ly are not independent for a given cross-sectional area. In this study, Ly (shorter edges length) is always less than Lx (longer edges length). With the increase in the Lx, the Ly gradually reduces, as shown in Figure 6d. Thus, the γavg of the rectangular pebble beds with different bed dimensions are displayed in 3D views, as shown in Figure 6a. The edge lengths of the x and y sides are as the horizontal plane, the γavg is as the vertical axis, and the points for each specific cross-sectional area are joined to form a profile. When the profiles are projected to the Lx-γavg, Ly-γavg, and Lx-Ly planes, the results can be presented in the form of a line chart, as shown in Figure 6b,d.
Figure 6 shows that both the aspect ratio and cross-sectional area of the rectangular tube affect the packing fractions of the rectangular pebble beds. As the aspect ratio of the rectangular tube increases, the γavg gradually decreases, as shown in Figure 6b,c, which is perhaps due to the increasing aspect ratio of the rectangular cross-section. The longer edge length (Lx) is gradually increasing, while the shorter edge length (Ly) is gradually decreasing, as shown in Figure 6d, which leads to the cross-sectional perimeter of the rectangular tube gradually increasing, as shown in Figure 7a. In turn, the proportion of the region affected by the fixed wall gradually increases in the rectangular pebble bed. The γlocal in the near-wall region is always smaller than that in the bulk region of the pebble bed. Thus, the γavg of the whole pebble bed decreases gradually with the increase in aspect ratios, as shown in Figure 6b,c and Figure 7b. The fixed-wall effect in the local packing structures of the rectangular pebble beds will be discussed in detail in Section 3.3.
Furthermore, a pebble bed can be treated as a randomly packed granular material. These disordered granular systems always form stable packing structures when unperturbed. However, in the presence of external interferences, such as taping, vibrating, or shear, they relax and become a complex-in-nature fluid [63]. Therefore, by referring to the flow dynamics in the rectangular tube, the equivalent hydraulic diameter De of the rectangular tube was calculated to reveal the effect of aspect ratio changes in the cross-section of the rectangular tube on the packing performance of the pebble bed. It should be noted that the equivalent hydraulic diameter here is for a rectangular tube and not a pebble bed. Thus, the De of the rectangular tube is determined by the formula De = 4A/C = 4A/(2Lx + 2Ly) = 2(Lx× Ly)/(Lx + Ly). The calculated De of the rectangular tube is plotted in Figure 7c.
Figure 7 shows that when the cross-sectional area is fixed, the De of the rectangular tubes decreases gradually with the increase in the aspect ratio α of the rectangular tubes, which might be the reason that the γavg of the rectangular pebble bed decreases gradually with the increase in aspect ratio α. Such as, the γavg also increases with the increase in the ratios of cylinder diameter to pebble diameter for the cylindrical pebble beds [8] and the ratios of the side length to pebble diameter for the square pebble beds [7,8], respectively. Similarly, Figure 7d shows the variation in the γavg of the pebble bed with the De of the rectangular tubes with the different cross-sectional areas. The results demonstrate that the γavg of the rectangular pebble bed shows a rapid increase trend with the increase in the De of the rectangular tubes, which further explains the main reason why the γavg of the pebble bed decreases with the increase in the aspect ratio, as shown in Figure 5, Figure 6 and Figure 7. In other words, the De of the rectangular tube gradually decreases with the increase in the aspect ratio α, which leads to the decrease in the γavg of the rectangular pebble beds.

3.3. Local Packing Fraction Distribution

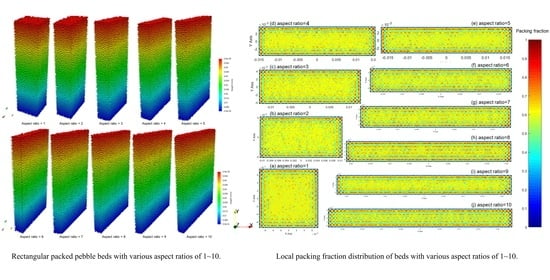
3.3.1. Effect of the Aspect Ratio of Rectangular Tube

To reveal the effects of the fixed wall and aspect ratio on the packing structures, the local packing fraction (γlocal) was calculated based on the line-averaged method. The detailed calculation method can refer to the literature [30,46]. Taking a rectangular pebble bed with a cross-sectional area of 225 d2 as an example, the γlocal is shown in Figure 8. It is demonstrated that both the aspect ratio and fixed wall significantly influence the pebble packing in rectangular tubes. As the aspect ratio α increases, the influence of the fixed wall on the local packing structure becomes more and more significant. For instance, a relatively uniform γlocal is observed in the inner region of the rectangular pebble bed when the aspect ratio equals 1. The layered distribution of γlocal is limited in the region of 4–5 d close to the tube wall. When the aspect ratio increases to 3, only a tiny part of the γlocal reaches a stable value in a narrow range at the middle of the pebble bed. When the aspect ratio α increases to 10, the γlocal in the entire pebble bed is affected by the fixed wall. For example, along the direction parallel to the x-axis (longer edge), the γlocal presents a layered distribution with five high local packing fraction layers. This is predominantly because the length of the shorter edge of the rectangular tube decreases as the aspect ratio α increases. When the side length of the shorter edge is less than 10 d, the wall effect affects the entire rectangular pebble bed. As the length of the shorter edge is further reduced, the influence of the wall effect on the γlocal will become more and more significant.
In the corner areas of the pebble beds, the γlocal is significantly affected by aspect ratio α and the fixed wall. When the aspect ratio is 1, the pebble-packing structure is affected by two mutually perpendicular walls. Several spot-like areas with high γlocal can be observed near the apex points or corners of the rectangle, essentially due to the regular packing of the pebble under the influence of the two mutually perpendicular fixed walls. With the aspect ratio increase, since the shorter edge length is further reduced, the pebble packing in the corner region will be affected more by the fixed walls. It can lead to a more regular packing structure and a more apparent spot-like distribution of the γlocal close to the corner regions.
Further, the pebble center distribution was plotted in Figure 9 by projecting the pebble center on the x-y plane to comprehensively reveal the influences of the wall effect and the aspect ratio. Each blue dot represents the pebble center. The black lines indicate the fixed sidewalls. Figure 9 clearly shows the layered distribution characteristics of the pebble packing in the area close to the fixed sidewalls. In the corner zones, the pebble center distribution shows the characteristic of a grid intersection. With the increase in aspect ratio, the grid-like distribution of pebble centers becomes more and more marked close to the corners and shorter edges, which is due to the influence of the wall effect and is consistent with the distribution of the γlocal in Figure 8.
In addition, the γaxi of the rectangular pebble beds with different aspect ratios α were also computed to reveal the effects of the fixed wall and the aspect ratio on the packing structures. The γaxi of rectangular pebble beds with a cross-sectional area of 225 d2 and aspect ratios of 1–10 are displayed in Figure 10, respectively. The effect of the fixed tube wall and the aspect ratio on the γaxi distribution can be observed clearly. It can be seen from Figure 10a that with the increase in aspect ratio, γaxi along the x-axis oscillates near the wall, and the proportion of the stable packing fraction in the middle zone of the bed increases gradually. This is mainly because the fixed-wall effect in a packed pebble bed is always limited in the range of 4–5 d close to a fixed wall in a randomly packed pebble bed [34], which causes γaxi to oscillate markedly only in the zone of 4–5 d close to the wall. These several peaks of the γaxi near the fixed wall correspond to the layered distributed regions of high local packing fractions, as shown in Figure 8, and the layered sphere packing characteristics in Figure 9. When the distance to the fixed wall increases to larger than 5 d, a stable packing fraction can be obtained. As the aspect ratio α of the rectangular tube increases, the longer edge length along the x-axis gradually increases, so the stable region of the γaxi gradually increases. On the contrary, Figure 10b reveals that the percentage of the stable region of the γaxi along the y-axis gradually decreases as the aspect ratio α of the pebble bed increases. The main reason is that with the increase in the aspect ratio α, the length of the side edge along the y-axis gradually decreases, resulting in the gradual reduction in the stable region of the γaxi along the y-axis.

3.3.2. Effect of the Cross-Sectional Area of Rectangular Tube

For the pebble bed in the rectangular tubes with different cross-sectional areas, the γlocal in the pebble bed with various cross-sectional areas and a fixed aspect ratio of 5 in the x-y plane is shown in Figure 11. It is revealed that the cross-sectional areas of the rectangular tubes have a pronounced effect on the distribution of γlocal, especially the pebble bed in the tubes with a smaller cross-sectional area. For instance, when the cross-sectional area is 100 d2, there are several spot-like regions with high γlocal at the two ends of the rectangular bed along the x-axis. In contrast, in the inner middle region of the pebble bed along the x-axis, the high local packing fraction exhibits a layered distribution. There are five layers when the cross-sectional area is 100 d2. This is mainly because the edge lengths along the x-axis and y-axis are 22.36 d and 4.47 d, respectively. The inner regions of the container can only be filled with about 4.47 layered pebbles. The pebble packing is affected by three fixed sidewalls.
In addition, as can be seen from Figure 11, with the increase in the cross-sectional areas of the rectangular tubes, the influence of the wall effect on the packing characteristics (packing fraction, pebble center distribution) gradually weakens. A uniform distribution area of the packing fraction appears in the inner region of the rectangular pebble bed, which corresponds to the uniformly random pebble-packing state, as illustrated by the uniformly distributed region of the pebble center in Figure 12.
To reveal the influences of the wall effect and cross-sectional area on packing structure, the γaxi of the pebble beds in the rectangular tubes have also been calculated. Figure 13 shows the γaxi along the x-axis and y-axis in the rectangular pebble beds with aspect ratios of 5, respectively. The results show that γaxi oscillates considerably close to the fixed walls due to the influence of the wall effect. As the distances to the fixed walls increase, the amplitude of γaxi gradually decays. A stable value can be obtained in the inner bulk region of the rectangular pebble bed. Additionally, with the increase in cross-sectional area, the proportion of the wall-affected region of γaxi gradually decreases. A stable γaxi can be achieved in a broader region in the pebble bed.
Along the x-axis, with the increase in the cross-sectional area and aspect ratio of the rectangular tubes, the percentage of the wall-affected zone of the γaxi of the pebble bed gradually decreases. This is mainly because as the cross-sectional area and the aspect ratio increase, the length of the longer edge along the x-axis direction gradually increases. However, the absolute value of the fixed-wall-affected region is always limited to 4–5 d close to the fixed wall. On the contrary, in the direction along the y-axis, the percentage of the stable zone of γaxi gradually increases as the cross-sectional area increases. It gradually decreases with the increase in the aspect ratio α. The main reason is that the shorter edge length along the y-axis gradually increases with the cross-sectional area of the rectangular tubes. However, it gradually decreases with the increase in the aspect ratio, which results in the percentage of the stable region of γaxi along the y-axis gradually decreasing.

3.4. Coordination Number Distribution

3.4.1. Average Coordination Number

The coordination number (CN) is closely related to the packing fraction and contact force chain. The coordination number is the number of surrounding pebbles in contact with the pebble under consideration. Figure 14 shows the average coordination number (CNavg) of the rectangular pebble beds with different cross-sectional areas and aspect ratios. When the cross-sectional area is fixed, CNavg gradually declines with the increase in the aspect ratio, as shown in Figure 14a. The decline rate of CNavg of a pebble bed with a relatively small cross-sectional area is significantly higher than that of a pebble bed with a relatively large cross-sectional area. This is predominantly because the CNavg is closely related to the packing structure. Additionally, due to the influence of the wall effect, the pebbles in direct contact with and close to the fixed walls have relatively small coordination numbers. As the aspect ratio increases, the wall-affected region’s proportion gradually grows, resulting in a reduction in the CNavg.
In addition, Figure 14b shows the CNavg of the rectangular pebble beds with various pebble-bed scales in terms of the cross-sectional area. The results show that the CNavg gradually increases as the pebble-bed scale increases. When the cross-sectional area is less than 900 d2, CNavg increases rapidly as the cross-sectional area increases. When the cross-sectional area is larger than 900 d2, CNavg gradually reaches a stable value. Similarly, Figure 14c shows the CNavg as dependent on the De of the rectangular duct. With the increase in the De, the CNavg inside the rectangular pebble bed gradually increases and stabilizes when the De is larger than 30 d, which is consistent with the variation in the γavg in Figure 7d. This is also mainly because the pebbles in contact with and near the walls have a relatively small coordination number and lower packing fraction due to the fixed-wall effect. As the cross-sectional area increases, the proportion of the fixed-wall-affected region gradually decreases. As a result, both the CNavg and the γavg of the pebble bed increase gradually. In addition, a positive correlation between the CNavg and γavg was found, as shown in Figure 14d. The γavg increases with the increase in the CNavg of the rectangular pebble bed. Through curve fitting, the relationship between the average packing fraction and the average coordination number can be obtained as follows:
γ x = − 0.0676   x 2 + 0.8463   x − 2.0257 ,     4.75 < x < 6.125 ,
where x is the CNavg.

3.4.2. Coordination Number Distribution

Figure 15 shows the probability distribution of the coordination numbers in the rectangular beds with different aspect ratios and cross-sectional areas. The coordination number is distributed in the range of 1–11. The coordination numbers with the highest probability in most rectangular pebble beds are 5 or 6. With the increase in the aspect ratio, the coordination numbers with the highest probability gradually decrease. On the contrary, the probability of a low coordination number gradually increases. For example, when the cross-sectional area is 100 d2, the coordination number with the highest probability is 5. As the aspect ratio gradually increases, the probability distribution curve of the CN shifts to the left. That is, the probability of the CN being less than five is gradually increasing, while the probability of the CN being larger than five is gradually decreasing. When the cross-sectional area is 225 d2, the highest probability coordination number decreases from 6 to 5 as the aspect ratio increases from 1 to 10.
In addition, with the further increase in the cross-sectional area of the pebble bed, the coordination number with the highest probability stabilizes at 6. When the cross-sectional area is greater than 400 d2, the coordination number with the highest probability is always equal to 6. The differences in the probability distribution curves of the CN become smaller and smaller and gradually coincide. This is mainly because as the cross-sectional area increases, the proportion of pebbles in contact with the fixed walls gradually decreases, and the influence of the wall effect becomes smaller and smaller, resulting in the CN distribution of the pebble bed gradually stabilizing.
Figure 16 shows the probability distribution of the CN in the rectangular pebble beds with different cross-sectional areas at fixed aspect ratios of 1, 4, 7, and 10. It can be seen from the figure that the change in the cross-sectional area has a significant impact on the probability distribution of the CN. When the aspect ratio is fixed, the most probable coordination number increases from 5 to 6 as the cross-sectional area increases. The probability of a low coordination number less than five gradually decreases, and the probability of a high coordination number larger than six gradually increases. The probability distribution curves of the CN shift to the right, demonstrating that the CNavg gradually increases with the increase in the cross-sectional area. The results are consistent with the conclusion in Figure 15 and prove that the packing fraction and packing density gradually increase with the increase in the cross-sectional area.

3.5. Radial Distribution Function

Radial distribution function (RDF) is a parameter to reveal the inner packing structure of granular material by the inter-pebble radial correlations therein, defined as the probability of finding one pebble center at a certain distance (the distance is always normalized by the pebble diameter from a given reference pebble center, determined as g r = Δ N r 4 π r 2 Δ r ρ o , where Δ N r is the number of pebble centers situated in the distance between r + Δr from the reference pebble center). ρ o is the average pebble number density in the bed. The RDFs of the whole pebble beds are the average RDFs of all similar pebbles. r is the normalized radial distance.
The RDFs of the rectangular pebble beds with different cross-sectional areas and aspect ratios are plotted in Figure 17 and Figure 18. The common characteristics of the RDFs of mono-sized pebble beds can be observed. Namely, the RDFs of mono-sized random packed pebble beds show the first sharp peaks at distance 1, which is caused by the pebbles in direct contact around the reference pebble. The split-second peaks at distances of 3 and 2 agree well with the results in Refs. [31,64,65].
In addition, it can be seen from Figure 17 that the aspect ratio of the rectangular container has a more significant effect on the RDFs of the pebble bed. As the aspect ratio increases, the values of the RDF decrease gradually. This is mainly because the bulk packing density of the pebble bed gradually decreases with the increase in the aspect ratio. The contact between pebbles and the surrounding pebbles gradually decreases, which can be reflected in the change of the average coordination number of the pebble bed in Figure 14a. With the increase in the pebble-bed scale in terms of the cross-sectional area of the pebble bed, however, the influence of the aspect ratio variation on the RDF values gradually decreases. The RDFs curves gradually overlap.
Further, Figure 18 reveals that the pebble-bed scale also significantly affects the RDFs of the pebble bed with fixed aspect ratios. As the cross-sectional area of the pebble bed increases, the RDF value gradually increases. This variation trend is more significant when far from the reference pebble center, such as the RDF values when the radial distance is greater than 4.5. That is to say, the change in the aspect ratio and the cross-sectional area of the rectangular container has little influence on the distribution characteristics in the short range of the RDFs of the whole pebble bed. For example, the first, second, and third peaks all appear at the radial distances of 1, 3 , and 2, which are common features of the RDF of the mono-sized pebble bed.
However, the variation in the aspect ratio and the cross-sectional area greatly influence the RDF values of the pebble bed. Figure 19 shows the RDFs’ first peak value and balance value. Both the first peak value and the asymptotic value gradually decrease with increasing aspect ratio. As the cross-sectional area of the pebble bed increases, the first RDF peak value gradually decreases, while the RDF asymptotic value gradually increases. This is mainly because the first peak value is due to the contribution of the pebbles in direct contact with the reference pebbles. When the cross-sectional area of the pebble bed is relatively small, the pebbles near the wall are more regularly packed due to the influence of the sidewall effect. So, the first RDF peak value is larger than that of the pebble bed with a larger cross-sectional area. The RDFs’ asymptotic value reflects the pebble bed’s overall characteristics. With the increase in the cross-sectional area of the pebble bed, the influence of the wall effect gradually decreases, and the proportion of randomly and uniformly packed pebbles inside the pebble bed gradually increases, with the RDF asymptotic value gradually increasing. When the wall effect is excluded entirely, the RDF asymptotic value of the whole pebble bed gradually approaches 1 when the radial distance is relatively long.

4. Conclusions

The packing characteristics of rectangular pebble beds packed with mono-sized pebbles were investigated by the DEM modeling method during our packing experiment. The effects of the aspect ratios of the rectangular container and the pebble-bed scales, in terms of cross-sectional area, and of the rectangular pebble bed on the packing characteristics (such as average packing fraction, local packing fraction distribution, coordination number, radial distribution function) were analyzed in detail. The results obtained in this work reveal that the aspect ratio and the bed scale in terms of the cross-sectional area significantly influence the packing characteristics of a rectangular mono-sized pebble bed. As the aspect ratio of the rectangular container increases, the average packing fraction and the average coordination number gradually decrease. As the cross-sectional area of the rectangular container increases, both the average packing fraction and the average coordination number increase gradually. Furthermore, an apparent wall effect on the axial and local packing fractions can be observed close to the fixed walls. With the increase in the aspect ratios, the wall effect becomes more and more evident. However, as the cross-sectional area increases, the proportion of the wall-affected region gradually decreases. In addition, the cross-sectional area and the aspect ratio have little effect on the distribution characteristics of RDFs but have a significant effect on the RDF values of the pebble bed. With the increase in the aspect ratio, the first peak value and the asymptotic value of RDFs gradually decrease. As the cross-sectional area increases, the first RDF peak value gradually decreases while the RDF asymptotic value gradually increases.
The results and conclusion in this work will provide a reference for the design optimization of the tritium breeder blankets of nuclear fusion reactors, as well as an analysis of heat and mass transfer in the microchannel pebble-bed catalytic reactor. For instance, the packing fraction of pebble beds can be used for the neutron analysis of the tritium breeding blanket. Porosity and coordination number can be used to evaluate the heat- and mass-transfer processes of the micro-channel pebble-bed catalytic reactors, the tritium breeder pebble-bed in a fusion blanket, and so forth. Research on heat-transfer behaviors will be conducted in the future.

Author Contributions

Conceptualization, B.G., J.Y., L.W. and Y.F.; methodology, B.G., H.C., L.W. and Y.F.; software, B.G. and H.C.; validation, B.G. and H.C.; formal analysis, B.G.; investigation, B.G.; data curation, B.G.; writing—original draft preparation, B.G.; writing—review and editing, B.G., H.C., J.Y., L.W., Y.F. and X.W.; visualization, B.G. and H.C.; supervision, Y.F. and X.W.; project administration, X.W.; funding acquisition, Y.F. and X.W. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the National Key Research and Development Program of China under Grant No. 2022YFE03210100, 2017YFE0300602; the National Natural Science Foundation of China under Grant No. 11905047; and the Natural Science Foundation of Sichuan, China, under grant number 2022NSFSC1216.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data are available from the corresponding author upon reasonable requests.

Acknowledgments

The authors acknowledge the technical support of the HPC Platform, Southwestern Institute of Physics.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Mederos, F.S.; Ancheyta, J.; Chen, J. Review on criteria to ensure ideal behaviors in trickle-bed reactors. Appl. Catal. A-Gen. 2009, 355, 1–19. [Google Scholar] [CrossRef]
  2. Jiang, S.; Tu, J.; Yang, X.; Gui, N. A review of pebble flow study for pebble bed high temperature gas cooled reactor. Exp. Comput. Multiph. Flow 2019, 1, 159–176. [Google Scholar] [CrossRef] [Green Version]
  3. Gui, N.; Huang, X.; Yang, X.; Tu, J.; Jiang, S. HTR-PM-based 3D pebble flow simulation on the effects of base angle, recirculation mode and coefficient of friction. Ann. Nucl. Energy 2020, 143, 107442. [Google Scholar] [CrossRef]
  4. Wu, M.; Gui, N.; Wu, H.; Yang, X.; Tu, J.; Jiang, S. Effects of density difference and loading ratio on pebble flow in a three-dimensional two-region-designed pebble bed. Ann. Nucl. Energy 2019, 133, 924–936. [Google Scholar] [CrossRef]
  5. Wang, X. Preliminary Design and Tritium Assessment of CFETR HCCB TBB, Paper No. O1B.5. In In Proceedings of the 12th International Conference on Tritium Science & Technology, Busan, Korea, 22–26 April 2019. [Google Scholar]
  6. Wu, X.; Liao, H.; Wang, X.; He, K.; Wang, S.; Cao, Q.; Zhou, B.; Hu, Z.; Li, X.; Feng, K. Design optimization and analysis of CN HCCB TBM-set. Fusion Eng. Des. 2018, 136, 839–846. [Google Scholar] [CrossRef]
  7. Gong, B.; Feng, Y.; Liao, H.; Liu, Y.; Wang, X.; Feng, K. Discrete element modeling of pebble bed packing structures for HCCB TBM. Fusion Eng. Des. 2017, 121, 256–264. [Google Scholar] [CrossRef]
  8. Gong, B.; Feng, Y.; Liao, H.; Wu, X.; Wang, S.; Wang, X.; Feng, K. Numerical investigation of the pebble bed structures for HCCB TBM. Fusion Eng. Des. 2018, 136, 1444–1451. [Google Scholar] [CrossRef]
  9. Kawamura, Y.; Tanigawa, H.; Hirose, T.; Gwon, H.; Nakajima, M.; Takemura, M.; Nakata, M.; Ishioka, M.; Yoshino, S.; Murakami, H.; et al. Status of water cooled ceramic breeder blanket development. Fusion Eng. Des. 2018, 136, 1550–1556. [Google Scholar] [CrossRef]
  10. Lei, M.; Xu, S.; Wang, J.; Song, Y.; Liu, S.; Lu, K.; Xu, K.; Pei, K. Preliminary assessment on safety performance of updated HCCB blanket module for CFETR. Fusion Eng. Des. 2018, 131, 77–83. [Google Scholar] [CrossRef]
  11. Wang, J.; Lei, M.; Yang, H.; Xu, S.; Xu, K.; Yin, Z.; Li, C.; Zhao, P.; Song, Y. Study on the packing characteristics of a special “J” shape ceramic packed pebble bed based on discrete element modeling. Powder Technol. 2021, 379, 362–372. [Google Scholar] [CrossRef]
  12. Fouda, Y.M.; Bayly, A.E. A DEM study of powder spreading in additive layer manufacturing. Granul. Matter 2020, 22, 10. [Google Scholar] [CrossRef] [Green Version]
  13. Wei, H.; Ge, Y.; Li, M.; Li, Y.; Saxén, H.; He, Z.; Yu, Y. DEM study of the porosity distribution of pellet sandpile formed by ternary size particles. Powder Technol. 2020, 360, 1337–1347. [Google Scholar] [CrossRef]
  14. Ghodki, B.M.; Patel, M.; Namdeo, R.; Carpenter, G. Calibration of discrete element model parameters: Soybeans. Comput. Part. Mech. 2019, 6, 3–10. [Google Scholar] [CrossRef]
  15. Jian, F.; Narendran, R.B.; Jayas, D.S. Segregation in stored grain bulks: Kinematics, dynamics, mechanisms, and minimization—A review. J. Stored Prod. Res. 2019, 81, 11–21. [Google Scholar] [CrossRef]
  16. Singh, H.; Saini, R.; Saini, J. A review on packed bed solar energy storage systems. Renew. Sustain. Energy Rev. 2010, 14, 1059–1069. [Google Scholar] [CrossRef]
  17. Guo, Z.; Sun, Z.; Zhang, N.; Ding, M. Influence of confining wall on pressure drop and particle-to-fluid heat transfer in packed beds with small D/d ratios under high Reynolds number. Chem. Eng. Sci. 2019, 209, 115200. [Google Scholar] [CrossRef]
  18. Wongkham, J.; Wen, T.; Lu, B.; Cui, L.; Xu, J.; Liu, X. Particle-resolved simulation of randomly packed pebble beds with a novel fluid-solid coupling method. Fusion Eng. Des. 2020, 161, 111953. [Google Scholar] [CrossRef]
  19. Zhao, Z.; Feng, K.; Feng, Y. Theoretical calculation and analysis modeling for the effective thermal conductivity of Li4SiO4 pebble bed. Fusion Eng. Des. 2010, 85, 1975–1980. [Google Scholar] [CrossRef]
  20. Chen, L.; Wang, C.; Moscardini, M.; Kamlah, M.; Liu, S. A DEM-based heat transfer model for the evaluation of effective thermal conductivity of packed beds filled with stagnant fluid: Thermal contact theory and numerical simulation. Int. J. Heat. Mass. Tran. 2019, 132, 331–346. [Google Scholar] [CrossRef]
  21. Kim, S.G.; Addad, Y.; Liu, M.; Lee, J.I.; Lee, Y. Computational investigation into heat transfer coefficients of randomly packed pebbles in flowing FLiBe. Inter. J. Heat Mass Transf. 2019, 145, 118769. [Google Scholar] [CrossRef]
  22. Sohn, D.; Lee, Y.; Ahn, M.-Y.; Park, Y.-H.; Cho, S. Numerical prediction of packing behavior and thermal conductivity of pebble beds according to pebble size distributions and friction coefficients. Fusion Eng. Des. 2018, 137, 182–190. [Google Scholar] [CrossRef]
  23. Mandal, D.; Sathiyamoorthy, D.; Vinjamur, M. Void fraction and effective thermal conductivity of binary particulate bed. Fusion Eng. Des. 2013, 88, 216–225. [Google Scholar] [CrossRef]
  24. Ying, A.; Reimann, J.; Boccaccini, L.; Enoeda, M.; Kamlah, M.; Knitter, R.; Gan, Y.; van der Laan, J.G.; Magielsen, L.; Di Maio, P.; et al. Status of ceramic breeder pebble bed thermo-mechanics R&D and impact on breeder material mechanical strength. Fusion Eng. Des. 2021, 87, 1130–1137. [Google Scholar]
  25. Zhou, W.; Xu, K.; Ma, G.; Yang, L.; Chang, X. Effects of particle size ratio on the macro- and microscopic behaviors of binary mixtures at the maximum packing efficiency state. Granum. Matter 2016, 18, 81. [Google Scholar] [CrossRef]
  26. Annabattula, R.; Gan, Y.; Kamlah, M. Mechanics of binary and polydisperse spherical pebble assembly. Fusion Eng. Des. 2012, 87, 853–858. [Google Scholar] [CrossRef]
  27. Donne, M.D.; Goraieb, A.; Piazza, G.; Scaffidi-Argentina, F. Experimental investigations on the thermal and mechanical behaviour of a binary beryllium pebble bed. Fusion Eng. Des. 2000, 49–50, 521–528. [Google Scholar] [CrossRef]
  28. van Antwerpen, W.; Toit, C.; Rousseau, P. A review of correlations to model the packing structure and effective thermal conductivity in packed beds of mono-sized spherical particles. Nucl. Eng. Des. 2010, 240, 1803–1818. [Google Scholar] [CrossRef]
  29. von Seckendorff, J.; Hinrichsen, O. Review on the structure of random packed-beds. Can. J. Chem. Eng. 2021, 99, S703–S733. [Google Scholar] [CrossRef]
  30. Feng, Y.; Gong, B.; Cheng, H.; Luo, X.; Wang, L.; Wang, X. Effects of bed dimension, friction coefficient and pebble size distribution on the packing structures of the pebble bed for solid tritium breeder blanket. Fusion Eng. Des. 2021, 163, 112156. [Google Scholar] [CrossRef]
  31. Feng, Y.; Gong, B.; Cheng, H.; Wang, L.; Wang, X. Effects of fixed wall and pebble size ratio on packing properties and contact force distribution in binary-sized pebble mixed beds at the maximum packing efficiency state. Powder Technol. 2021, 390, 504–520. [Google Scholar] [CrossRef]
  32. Gong, B.; Cheng, H.; Feng, Y.; Luo, X.; Wang, L.; Wang, X. Effect of pebble size distribution and wall effect on inner packing structure and contact force distribution in tritium breeder pebble bed. Energies 2021, 14, 449. [Google Scholar] [CrossRef]
  33. Gong, B.; Feng, Y.; Yu, G.; Liao, H.; Wang, X.; Feng, K. Experimental investigation of the effect of particle size on the effective thermal properties of particle beds. J. Eng. Thermophys. 2019, 40, 1151–1159. [Google Scholar]
  34. Reimann, J.; Vicente, J.; Ferrero, C.; Rack, A.; Gan, Y. 3D tomography analysis of the packing structure of spherical particles in slender prismatic containers. Int. J. Mater. Res. 2020, 111, 65–77. [Google Scholar] [CrossRef]
  35. Reimann, J.; Vicente, J.; Brun, E.; Ferrero, C.; Gan, Y.; Rack, A. X-ray tomography investigations of monosized sphere packing structures in cylindrical containers. Powder Technol. 2017, 318, 471–483. [Google Scholar] [CrossRef]
  36. Liu, Y.; Yu, Z.; Yang, J.; Wassgren, C.; Curtis, J.S.; Guo, Y. Discrete Element Method Investigation of Binary Granular Flows with Different Particle Shapes. Energies 2020, 13, 1841. [Google Scholar] [CrossRef] [Green Version]
  37. Yuan, Y.; Liu, L.; Zhuang, Y.; Jin, W.; Li, S. Coupling effects of particle size and shape on improving the density of disordered polydisperse packings. Phys. Rev. E 2018, 98, 042903. [Google Scholar] [CrossRef]
  38. Wang, J.; Lei, M.; Yang, H.; Xu, K.; Xu, S.; Zhao, P.; Song, Y. Effects of coefficient of friction and coefficient of restitution on static packing characteristics of polydisperse spherical pebble bed. Particuology 2021, 57, 1–9. [Google Scholar] [CrossRef]
  39. du Toit, C.G. Radial variation in porosity in annular packed beds. Nucl. Eng. Des. 2008, 238, 3073–3079. [Google Scholar] [CrossRef]
  40. Ren, C.; Yang, X.; Sun, Y. Porous Structure Analysis of the Packed Beds in a High-Temperature Reactor Pebble Bed Modules Heat Transfer Test Facility. Chin. Phys. Lett. 2013, 30, 022801. [Google Scholar] [CrossRef]
  41. Wang, J.; Lei, M.; Xu, S.; Yang, H.; Zhao, P.; Xu, K.; Song, Y. DEM simulation of mechanical behavior in one-dimensional compression of crushable ceramic pebble bed. Fusion Eng. Des. 2021, 168, 112606. [Google Scholar] [CrossRef]
  42. Reimann, J.; Brun, E.; Ferrero, C.; Vicente, J. Pebble bed structures in the vicinity of concave and convex walls. Fusion Eng. Des. 2015, 98–99, 1855–1858. [Google Scholar] [CrossRef]
  43. Buchlin, J.; Riethmuller, M.; Ginoux, J. A fluorescence method for the measurement of the local voidage in random packed beds. Chem. Eng. Sci. 1977, 32, 1116–1119. [Google Scholar] [CrossRef]
  44. Beavers, G.S.; Sparrow, E.M.; Rodenz, D.E. Influence of Bed Size on the Flow Characteristics and Porosity of Randomly Packed Beds of Spheres. J. Appl. Mech. 1973, 40, 655–660. [Google Scholar] [CrossRef]
  45. Desu, R.; Moorthy, A.; Annabattula, R. DEM simulation of packing mono-sized pebbles into prismatic containers through different filling strategies. Fusion Eng. Des. 2018, 127, 259–266. [Google Scholar] [CrossRef]
  46. Hamzah, A.B.; Ookawara, S.; Yoshikawa, S.; Matsumoto, H. Numerical study on porosity distribution and hydrodynamics of packed bed in narrow square channels. Chem. Eng. Process. 2020, 151, 107905. [Google Scholar] [CrossRef]
  47. Wang, S.; Wang, S.; Chen, H. Numerical influence analysis of the packing structure on ceramic breeder pebble beds. Fusion Eng. Des. 2019, 140, 41–47. [Google Scholar] [CrossRef]
  48. Taguchi, I.; Kurashige, M.; Imai, K. Effects of Cubic Container’s Wall or Floor on Random Packing Structures of Spherical Particles. JSME Int. J. 2006, 49, 265–272. [Google Scholar] [CrossRef] [Green Version]
  49. Zobel, N.; Eppinger, T.; Behrendt, F.; Kraume, M. Influence of the wall structure on the void fraction distribution in packed beds. Chem. Eng. Sci. 2012, 71, 212–219. [Google Scholar] [CrossRef]
  50. Jaggannagari, S.R.; Desu, R.K.; Reimann, J.; Gan, Y.; Moscardini, M.; Annabattula, R.K. DEM simulations of vibrated sphere packings in slender prismatic containers. Powder Technol. 2021, 393, 31–59. [Google Scholar] [CrossRef]
  51. Oğuz, E.C.; Marechal, M.; Ramiro-Manzano, F.; Rodriguez, I.; Messina, R.; Meseguer, F.J.; Löwen, H. Packing Confined Hard Spheres Denser with Adaptive Prism Phases. Phys. Rev. Lett. 2012, 109, 218301. [Google Scholar] [CrossRef] [Green Version]
  52. Pistocchini, L.; Garone, S.; Motta, M. Porosity and pressure drop in packed beds of spheres between narrow parallel walls. Chem. Eng. J. 2016, 284, 802–811. [Google Scholar] [CrossRef]
  53. Romkes, S.; Dautzenberg, F.; Bleek, C.V.D.; Calis, H. CFD modelling and experimental validation of particle-to-fluid mass and heat transfer in a packed bed at very low channel to particle diameter ratio. Chem. Eng. J. 2003, 96, 3–13. [Google Scholar] [CrossRef]
  54. Bauer, T.; Haase, S. Comparison of structured trickle-bed and monolithic reactors in Pd-catalyzed hydrogenation of alpha-methylstyrene. Chem. Eng. J. 2011, 169, 263–269. [Google Scholar] [CrossRef]
  55. Cundall, P.A.; Strack, O.D.L. A discrete numerical model for granular assemblies. Géotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
  56. Ding, W.; Chen, R.; Tian, W.; Qiu, S.; Su, G. Numerical investigation of dynamic characteristics of debris bed formation based on CFD-DEM method. Ann. Nucl. Energy 2023, 180, 109492. [Google Scholar] [CrossRef]
  57. Ding, W.; Xiao, X.; Cai, Q.; Chen, R.; Guo, K.; Tian, W.; Qiu, S.; Su, G. Numerical investigation of fluid–solid interaction during debris bed formation based on MPS-DEM. Ann. Nucl. Energy 2022, 175, 109244. [Google Scholar] [CrossRef]
  58. Chen, R.; Guo, K.; Zhang, Y.; Tian, W.; Qiu, S.; Su, G.H. Numerical analysis of the granular flow and heat transfer in the ADS granular spallation target. Nucl. Eng. Des. 2018, 330, 59–71. [Google Scholar] [CrossRef]
  59. Guo, K.; Chen, R.; Li, Y.; Qiu, S.; Su, G. Numerical investigation of the fluid-solid mixture flow using the FOCUS code. Prog. Nucl. Energy 2017, 97, 197–213. [Google Scholar] [CrossRef] [Green Version]
  60. Wu, Z.; Wu, Y.; Tang, S.; Liu, D.; Qiu, S.; Su, G.; Tian, W. DEM-CFD simulation of helium flow characteristics in randomly packed bed for fusion reactors. Prog. Nucl. Energy 2018, 109, 29–37. [Google Scholar] [CrossRef]
  61. LIGGGHTS(R)-PUBLIC Documentation, Version 3. X. Available online: http://www.liggghts.com (accessed on 2 November 2022).
  62. Kloss, C.; Goniva, C.; Hager, A.; Amberger, S.; Pirker, S. Models, algorithms and validation for opensource DEM and CFD-DEM. Prog. Comput. Fluid Dyn. Int. J. 2012, 12, 140–152. [Google Scholar] [CrossRef]
  63. Kou, B.; Cao, Y.; Li, J.; Xia, C.; Li, Z.; Dong, H.; Zhang, A.; Zhang, J.; Kob, W.; Wang, Y. Granular materials flow like complex fluids. Nature 2017, 551, 360–363. [Google Scholar] [CrossRef] [Green Version]
  64. Yang, R.Y.; Zou, R.P.; Yu, A.B. Computer simulation of the packing of fine particles. Phys. Rev. E 2000, 62, 3900–3908. [Google Scholar] [CrossRef]
  65. Hopkins, A.B.; Stillinger, F.H.; Torquato, S. Disordered strictly jammed binary sphere packings attain an anomalously large range of densities. Phys. Rev. E 2013, 88, 022205. [Google Scholar] [CrossRef]
Energies 16 00570 g001 550
Figure 1. Filling process of the pebbles packed in rectangular containers.
Figure 1. Filling process of the pebbles packed in rectangular containers.
Energies 16 00570 g001
Energies 16 00570 g002 550
Figure 2. Comparison of the γavg of the pebble beds in square tubes.
Figure 2. Comparison of the γavg of the pebble beds in square tubes.
Energies 16 00570 g002
Energies 16 00570 g003 550
Figure 3. Rectangular pebble beds with aspect ratios of 1–10 and cross-sectional area of 225 d2.
Figure 3. Rectangular pebble beds with aspect ratios of 1–10 and cross-sectional area of 225 d2.
Energies 16 00570 g003
Energies 16 00570 g004 550
Figure 4. Rectangular pebble beds with an aspect ratio of 5 and cross-sectional areas of 100 d2–1600 d2.
Figure 4. Rectangular pebble beds with an aspect ratio of 5 and cross-sectional areas of 100 d2–1600 d2.
Energies 16 00570 g004
Energies 16 00570 g005 550
Figure 5. Average packing fraction of the rectangular packed pebble beds (a) as a function of the aspect ratios and (b) as a function of the cross-sectional areas of the pebble beds.
Figure 5. Average packing fraction of the rectangular packed pebble beds (a) as a function of the aspect ratios and (b) as a function of the cross-sectional areas of the pebble beds.
Energies 16 00570 g005
Energies 16 00570 g006 550
Figure 6. Average packing fraction of the rectangular packed pebble beds with various bed dimensions: (a) 3D views, (b) projected to the Lx-γavg plane, (c) projected to the Ly-γavg plane, (d) projected to the Lx-Ly plane (bottom plane) (Color online).
Figure 6. Average packing fraction of the rectangular packed pebble beds with various bed dimensions: (a) 3D views, (b) projected to the Lx-γavg plane, (c) projected to the Ly-γavg plane, (d) projected to the Lx-Ly plane (bottom plane) (Color online).
Energies 16 00570 g006
Energies 16 00570 g007 550
Figure 7. Average packing fraction of the rectangular packed pebble beds as a function of (a,b) the cross-sectional perimeter of the container; (c,d) the equivalent diameter of the container.
Figure 7. Average packing fraction of the rectangular packed pebble beds as a function of (a,b) the cross-sectional perimeter of the container; (c,d) the equivalent diameter of the container.
Energies 16 00570 g007
Energies 16 00570 g008 550
Figure 8. Local packing fraction distribution in the x-y planes of the rectangular pebble beds with a fixed cross-sectional area of 225 d2 and various aspect ratios of (a) 1, (b) 2, (c) 3, (d) 4, (e) 5, (f) 6, (g) 7, (h) 8, (i) 9, (j) 10 (Color online).
Figure 8. Local packing fraction distribution in the x-y planes of the rectangular pebble beds with a fixed cross-sectional area of 225 d2 and various aspect ratios of (a) 1, (b) 2, (c) 3, (d) 4, (e) 5, (f) 6, (g) 7, (h) 8, (i) 9, (j) 10 (Color online).
Energies 16 00570 g008
Energies 16 00570 g009 550
Figure 9. Pebble center distribution in the x-y planes of the rectangular pebble beds with a fixed cross-sectional area of 225 d2 and various aspect ratios of (a) 1, (b) 2, (c) 3, (d) 4, (e) 5, (f) 6, (g) 7, (h) 8, (i) 9, (j) 10 (Color online).
Figure 9. Pebble center distribution in the x-y planes of the rectangular pebble beds with a fixed cross-sectional area of 225 d2 and various aspect ratios of (a) 1, (b) 2, (c) 3, (d) 4, (e) 5, (f) 6, (g) 7, (h) 8, (i) 9, (j) 10 (Color online).
Energies 16 00570 g009
Energies 16 00570 g010 550
Figure 10. Axial packing fraction variations along (a) x-axis (longer edge) and (b) y-axis (shorter edge) in pebble beds with various aspect ratios of 1–10 and a fixed cross-sectional area of 225 d2 (Color online).
Figure 10. Axial packing fraction variations along (a) x-axis (longer edge) and (b) y-axis (shorter edge) in pebble beds with various aspect ratios of 1–10 and a fixed cross-sectional area of 225 d2 (Color online).
Energies 16 00570 g010
Energies 16 00570 g011 550
Figure 11. Local packing fraction distribution in the x-y planes of the rectangular pebble beds with a fixed aspect ratio of 5 and various cross-sectional areas of (a) 100 d2, (b) 225 d2, (c) 400 d2, (d) 900 d2, (e) 1600 d2 (Color online).
Figure 11. Local packing fraction distribution in the x-y planes of the rectangular pebble beds with a fixed aspect ratio of 5 and various cross-sectional areas of (a) 100 d2, (b) 225 d2, (c) 400 d2, (d) 900 d2, (e) 1600 d2 (Color online).
Energies 16 00570 g011
Energies 16 00570 g012 550
Figure 12. Pebble center distribution in the x–y plane of the rectangular pebble beds with a fixed aspect ratio of 5 and various cross-sectional areas of (a) 100 d2, (b) 225 d2, (c) 400 d2, (d) 900 d2, (e) 1600 d2.
Figure 12. Pebble center distribution in the x–y plane of the rectangular pebble beds with a fixed aspect ratio of 5 and various cross-sectional areas of (a) 100 d2, (b) 225 d2, (c) 400 d2, (d) 900 d2, (e) 1600 d2.
Energies 16 00570 g012
Energies 16 00570 g013 550
Figure 13. Axial packing fraction variations along the (a) x-axis (longer edge) and (b) y-axis (shorter edge) in pebble beds with a fixed aspect ratio of 5 and various cross-sectional areas of 100 d2–1600 d2 (Color online).
Figure 13. Axial packing fraction variations along the (a) x-axis (longer edge) and (b) y-axis (shorter edge) in pebble beds with a fixed aspect ratio of 5 and various cross-sectional areas of 100 d2–1600 d2 (Color online).
Energies 16 00570 g013
Energies 16 00570 g014 550
Figure 14. Average coordination number of the rectangular pebble bed: (a) variation as aspect ratio, (b) variation as cross-sectional area, (c) variation as De, (d) relationship between the CNavg and the γavg of the rectangular pebble beds.
Figure 14. Average coordination number of the rectangular pebble bed: (a) variation as aspect ratio, (b) variation as cross-sectional area, (c) variation as De, (d) relationship between the CNavg and the γavg of the rectangular pebble beds.
Energies 16 00570 g014
Energies 16 00570 g015 550
Figure 15. Coordination number distribution of the rectangular packed pebble beds with cross-sectional areas of (a) 100 d2, (b) 225 d2, (c) 400 d2, (d) 900 d2, (e) 1600 d2.
Figure 15. Coordination number distribution of the rectangular packed pebble beds with cross-sectional areas of (a) 100 d2, (b) 225 d2, (c) 400 d2, (d) 900 d2, (e) 1600 d2.
Energies 16 00570 g015
Energies 16 00570 g016 550
Figure 16. Effect of the cross-sectional area on the coordination number distribution of the rectangular pebble beds: (a) aspect ratio = 1, (b) aspect ratio = 4, (c) aspect ratio = 7, (d) aspect ratio = 10.
Figure 16. Effect of the cross-sectional area on the coordination number distribution of the rectangular pebble beds: (a) aspect ratio = 1, (b) aspect ratio = 4, (c) aspect ratio = 7, (d) aspect ratio = 10.
Energies 16 00570 g016
Energies 16 00570 g017 550
Figure 17. RDFs of the pebble beds with different aspect ratios α of 1–10 and cross-sectional areas of (a) 100 d2, (b) 400 d2, (c) 900 d2, (d) 1600 d2.
Figure 17. RDFs of the pebble beds with different aspect ratios α of 1–10 and cross-sectional areas of (a) 100 d2, (b) 400 d2, (c) 900 d2, (d) 1600 d2.
Energies 16 00570 g017
Energies 16 00570 g018 550
Figure 18. RDFs of the pebble beds with different cross-sectional bed areas of 100 d2–1600 d2 and aspect ratios of (a) α = 1, (b) α = 4, (c) α = 7, (d) α = 10.
Figure 18. RDFs of the pebble beds with different cross-sectional bed areas of 100 d2–1600 d2 and aspect ratios of (a) α = 1, (b) α = 4, (c) α = 7, (d) α = 10.
Energies 16 00570 g018
Energies 16 00570 g019 550
Figure 19. First peak value and asymptotic value of the RDFs of the rectangular pebble beds depend on (a,b) aspect ratios and (c,d) cross-sectional areas.
Figure 19. First peak value and asymptotic value of the RDFs of the rectangular pebble beds depend on (a,b) aspect ratios and (c,d) cross-sectional areas.
Energies 16 00570 g019
Table
Table 1. Parameters of pebbles used in DEM simulation.
Table 1. Parameters of pebbles used in DEM simulation.
ParametersValues
Young’s modulus (GPa)90
Poisson ratio0.24
Density (g/cm3)2.323
Restitution coefficient0.9
Static friction coefficient for pebble–pebble0.1
Static friction coefficient for pebble–wall0.1
Pebble diameter, d (mm)1.0
Height of pebble bed (mm)~ 60
Table
Table 2. Rectangular pebble-bed dimension used in the DEM simulations.
Table 2. Rectangular pebble-bed dimension used in the DEM simulations.
Scs = Lx × Ly100 d2225 d2400 d2900 d21600 d2
α = Lx/LyLx/LyLx/LyLx/LyLx/LyLx/Ly
110.00/10.0015.00/15.0020.00/20.0030.00/30.0040.00/40.00
214.14/7.0721.21/10.6128.28/14.1442.43/21.2156.57/28.28
317.32/5.7725.98/8.6634.64/11.5551.96/17.3269.28/23.09
420.00/5.0030.00/7.5040.00/10.0060.00/15.0080.00/20.00
522.36/4.4733.54/6.7144.72/8.9467.08/13.4289.44/17.89
624.49/4.0836.74/6.1248.99/8.1673.48/12.2597.98/16.33
726.46/3.7839.69/5.6752.92/7.5679.37/11.34105.83/15.12
828.28/3.5442.43/5.3056.57/7.0784.85/10.61113.14/14.14
930.00/3.3345.00/5.0060.00/6.6790.00/10.00120.00/13.33
1031.62/3.1647.43/4.7463.25/6.3294.87/9.49126.49/12.65
Table
Table 3. Experimental results of γavg of square packed pebble bed with different aspect ratios.
Table 3. Experimental results of γavg of square packed pebble bed with different aspect ratios.
Scale Ratios (Lx/d)Experimental Results
123Mean Value ± Std Dev
10.3720.59380.58990.58910.5909 ± 0.0025
15.5580.60530.60450.60530.6050 ± 0.0005
22.3640.61650.61760.61660.6169 ± 0.0006
26.2800.62150.62310.61880.6211 ± 0.0022
29.7490.62290.62490.62590.6246 ± 0.0015
33.5460.62460.62460.62510.6248 ± 0.0003
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Gong, B.; Cheng, H.; Yan, J.; Wang, L.; Feng, Y.; Wang, X. Effects of the Aspect Ratio and Cross-Sectional Area of Rectangular Tubes on Packing Characteristics of Mono-Sized Pebble Beds. Energies 2023, 16, 570. https://doi.org/10.3390/en16010570

AMA Style

Gong B, Cheng H, Yan J, Wang L, Feng Y, Wang X. Effects of the Aspect Ratio and Cross-Sectional Area of Rectangular Tubes on Packing Characteristics of Mono-Sized Pebble Beds. Energies. 2023; 16(1):570. https://doi.org/10.3390/en16010570

Chicago/Turabian Style

Gong, Baoping, Hao Cheng, Juemin Yan, Long Wang, Yongjin Feng, and Xiaoyu Wang. 2023. "Effects of the Aspect Ratio and Cross-Sectional Area of Rectangular Tubes on Packing Characteristics of Mono-Sized Pebble Beds" Energies 16, no. 1: 570. https://doi.org/10.3390/en16010570

APA Style

Gong, B., Cheng, H., Yan, J., Wang, L., Feng, Y., & Wang, X. (2023). Effects of the Aspect Ratio and Cross-Sectional Area of Rectangular Tubes on Packing Characteristics of Mono-Sized Pebble Beds. Energies, 16(1), 570. https://doi.org/10.3390/en16010570

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop