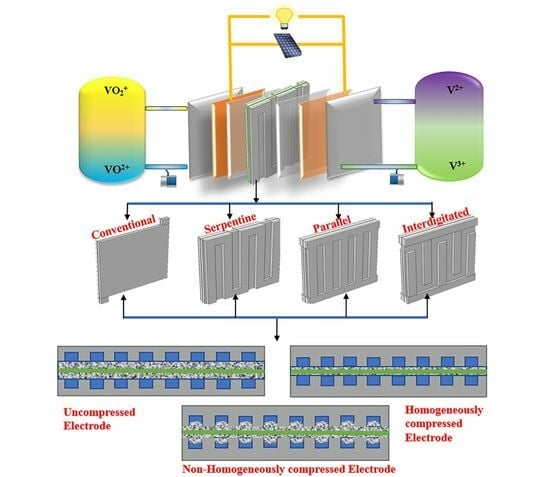
Hydrodynamic and Electrochemical Analysis of Compression and Flow Field Designs in Vanadium Redox Flow Batteries
Abstract
:1. Introduction
2. Model Development
2.1. Model Outline and Methodology
2.2. Model Assumptions
- The dilute solution is approximated using the principles of dilute solution theory.
- The flow is assumed to be single phase, specifically laminar and incompressible, since the majority of the liquid involved is water.
- The electrodes and membrane are considered to be isotropic (having uniform properties in all directions) and homogeneous (having uniform composition throughout).
- The system is assumed to be isothermal, meaning that there are no temperature variations, and no side reactions occur (such as the O2 and H2 gas evolution at the anode and cathode).
- Charged species are transported through the system via convection, migration, and diffusion.
- It is assumed that the reactant or charged ions do not leak through the cell’s outer surfaces.
- With the exception of protons, the membrane is impermeable/impervious to all other ions resulting from the reaction.
- The model accounts for the first dissociation of H+ ions but does not consider the second dissociation, as it is assumed to be consumed by the concentration of sulfate.
- The effect of gravity is neglected.
2.3. Governing Equations
2.3.1. Fluid Flow and Mass Transport
2.3.2. Electrochemical Reactions
Reaction Kinetics
Electrolyte
Membrane
Current Collector
- Activation overpotential (Eact): this overpotential arises from the electrochemical reactions occurring at the porous electrode.
- Concentration overpotential (Econ): this overpotential is a result of concentration changes within the battery.
- Ohmic overpotential (Eohm): this overpotential arises from the internal resistance of the battery.
2.4. Boundary Conditions
2.5. Numerical Method and Parameters
3. Results and Discussion
3.1. Grid Convergence Study
3.2. Model Validation
3.3. Effect of Flow Fields and Electrode Compression on Velocity and Pressure Drop
Velocity Profile
3.4. Influence of Electrode Compression on Cell Voltage
3.5. Influence of Flow Fields on Electrolyte Potential
3.6. Impact of Flow Fields on Overpotential Distribution
3.7. Impact of Flow Fields and Compression on Current Density Distribution
3.8. Influence of Compression in Flow Fields on Power Density
4. Conclusions
- The predicted cell performance of the non-homogeneously compressed electrode (a realistic operating condition) lies between the uncompressed and homogeneously compressed electrodes within the specified range of current density for all the flow field configurations considered in this study.
- It is observed that the Interdigitated flow field has displayed the best performance with the lowest charging potential and the highest discharging potential among all flow fields under all the three compression scenarios.
- Implementing cross flow in the flow field allows for an increased influx of reactants into the rib region, thereby enhancing overall mass transport within the battery.
- Near the corner of the rib, non-uniform current density distribution may give rise to hot spots during battery operation, potentially affecting performance and durability.
- It is observed that the non-homogeneous case study accurately predicts real cell performance and reveals notable variances in anticipated cell performance.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbol | |
| A | Specific surface area (m3/m2) |
| Concentration of each species (mol/m3) | |
| Di | Diffusion coefficient of each species (m2/s) |
| Di,eff | Effective diffusion coefficient of each species (m2/s) |
| df | Fibre diameter (m) |
| d | Depth of intrusion |
| E0 | Reference potential for the electrode reaction (V) |
| Equilibrium potential, negative electrode (V) | |
| Equilibrium potential, positive electrode (V) | |
| Reference potential, negative electrode (V) | |
| Reference potential, positive electrode (V) | |
| Donnan potential | |
| Reversible voltage (V) | |
| Cell voltage (V) | |
| Activation overpotential (V) | |
| Ohmic overpotential (V) | |
| Concentration overpotential (V) | |
| F | Faraday’s constant (96,485 C/mol) |
| Transfer current density (A/m2) | |
| Exchange current density (A/m2) | |
| Ionic current in the electrolyte (A/m2) | |
| Electronic current in the electrode (A/m2) | |
| K | Permeability of porous electrode (m2) |
| Kck | Kozeny–Carman constant |
| k | Rate constant (m/s) |
| Ni | Molar flux of species (mol/m2.s) |
| Pressure (Pa) | |
| Q | Mass source |
| R | Molar gas constant (8.31 J/(mol·K)) |
| SOC | State of charge |
| t | Thickness of electrode (m) |
| T | Cell temperature (K) |
| Species mobility (s·mol/kg) | |
| Velocity of ions in membrane (m/s) | |
| Local flow velocity vector (m/s) | |
| Valence of each species | |
| Greek | |
| ƞ | Overpotential (V) |
| Electrode potential (V) | |
| Electrolyte potential (V) | |
| Density (Kg/m3) | |
| Effective conductivity (S/cm) | |
| Viscosity (m2/s) | |
| Electrode porosity | |
| Transfer coefficient, negative electrode | |
| Overpotential, negative electrode (V) | |
| Subscript | |
| i | V2+, V3+, VO2+, VO2+, H+, HSO4− |
| 0 | Initial value |
| c | Compressed condition |
| Mem | Membrane property |
| Ref | Reference |
| Elec | Electrode property |
| Neg | Negative electrode |
| Pos | Positive electrode |
References
- Skyllas-Kazacos, M.; Rychcik, M.; Robins, R.G.; Fane, A.G.; Green, M.A. New All-Vanadium Redox Flow Cell. J. Electrochem. Soc. 1986, 133, 1057–1058. [Google Scholar] [CrossRef]
- Iwakiri, I.; Antunes, T.; Almeida, H.; Sousa, P.; Figueira, R.B. Redox Flow Batteries: Materials, Design and Prospects. Energies 2021, 14, 5643. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, H.; Li, X.; Zhang, J. Redox Flow Batteries; Zhang, H., Li, X., Zhang, J., Eds.; CRC Press: Boca Raton, FL, USA, 2017; Volume 2, ISBN 9781315152684. [Google Scholar]
- Aramendia, I.; Fernandez-Gamiz, U.; Martinez-San-Vicente, A.; Zulueta, E.; Lopez-Guede, J.M. Vanadium Redox Flow Batteries: A Review Oriented to Fluid-Dynamic Optimization. Energies 2020, 14, 176. [Google Scholar] [CrossRef]
- Lee, J.; Kim, J.; Park, H. Numerical Simulation of the Power-Based Efficiency in Vanadium Redox Flow Battery with Different Serpentine Channel Size. Int. J. Hydrogen Energy 2019, 44, 29483–29492. [Google Scholar] [CrossRef]
- Oh, K.; Won, S.; Ju, H. Numerical Study of the Effects of Carbon Felt Electrode Compression in All-Vanadium Redox Flow Batteries. Electrochim. Acta 2015, 181, 13–23. [Google Scholar] [CrossRef]
- Chang, T.C.; Zhang, J.P.; Fuh, Y.K. Electrical, Mechanical and Morphological Properties of Compressed Carbon Felt Electrodes in Vanadium Redox Flow Battery. J. Power Sources 2014, 245, 66–75. [Google Scholar] [CrossRef]
- Kumar, S.; Jayanti, S. Effect of Electrode Intrusion on Pressure Drop and Electrochemical Performance of an All-Vanadium Redox Flow Battery. J. Power Sources 2017, 360, 548–558. [Google Scholar] [CrossRef]
- Duan, Z.N.; Qu, Z.G.; Wang, Q.; Wang, J.J. Structural Modification of Vanadium Redox Flow Battery with High Electrochemical Corrosion Resistance. Appl. Energy 2019, 250, 1632–1640. [Google Scholar] [CrossRef]
- Bromberger, K.; Kaunert, J.; Smolinka, T. A Model for All-Vanadium Redox Flow Batteries: Introducing Electrode-Compression Effects on Voltage Losses and Hydraulics. Energy Technol. 2014, 2, 64–76. [Google Scholar] [CrossRef]
- Gundlapalli, R.; Jayanti, S. Effect of Electrode Compression and Operating Parameters on the Performance of Large Vanadium Redox Flow Battery Cells. J. Power Sources 2019, 427, 231–242. [Google Scholar] [CrossRef]
- Su, Z.Y.; Liu, C.T.; Chang, H.P.; Li, C.H.; Huang, K.J.; Sui, P.C. A Numerical Investigation of the Effects of Compression Force on PEM Fuel Cell Performance. J. Power Sources 2008, 183, 182–192. [Google Scholar] [CrossRef]
- Wang, Q.; Qu, Z.G.; Jiang, Z.Y.; Yang, W.W. Numerical Study on Vanadium Redox Flow Battery Performance with Non-Uniformly Compressed Electrode and Serpentine Flow Field. Appl. Energy 2018, 220, 106–116. [Google Scholar] [CrossRef]
- Park, S.K.; Shim, J.; Yang, J.H.; Jin, C.S.; Lee, B.S.; Lee, Y.S.; Shin, K.H.; Jeon, J.D. The Influence of Compressed Carbon Felt Electrodes on the Performance of a Vanadium Redox Flow Battery. Electrochim. Acta 2014, 116, 447–452. [Google Scholar] [CrossRef]
- You, D.; Zhang, H.; Chen, J. A Simple Model for the Vanadium Redox Battery. Electrochim. Acta 2009, 54, 6827–6836. [Google Scholar] [CrossRef]
- Xu, Q.; Zhao, T.S.; Leung, P.K. Numerical Investigations of Flow Field Designs for Vanadium Redox Flow Batteries. Appl. Energy 2013, 105, 47–56. [Google Scholar] [CrossRef]
- Yin, C.; Gao, Y.; Guo, S.; Tang, H. A Coupled Three Dimensional Model of Vanadium Redox Flow Battery for Flow Field Designs. Energy 2014, 74, 886–895. [Google Scholar] [CrossRef]
- Messaggi, M.; Canzi, P.; Mereu, R.; Baricci, A.; Inzoli, F.; Casalegno, A.; Zago, M. Analysis of Flow Field Design on Vanadium Redox Flow Battery Performance: Development of 3D Computational Fluid Dynamic Model and Experimental Validation. Appl. Energy 2018, 228, 1057–1070. [Google Scholar] [CrossRef]
- Ertugrul, T.Y.; Daugherty, M.C.; Houser, J.R.; Aaron, D.S.; Mench, M.M. Computational and Experimental Study of Convection in a Vanadium Redox Flow Battery Strip Cell Architecture. Energies 2020, 13, 4767. [Google Scholar] [CrossRef]
- Chang, C.-H.; Chou, H.-W.; Hsu, N.-Y.; Chen, Y.-S. Development of Integrally Molded Bipolar Plates for All-Vanadium Redox Flow Batteries. Energies 2016, 9, 350. [Google Scholar] [CrossRef]
- Wei, L.; Guo, Z.X.; Sun, J.; Fan, X.Z.; Wu, M.C.; Xu, J.B.; Zhao, T.S. A Convection-Enhanced Flow Field for Aqueous Redox Flow Batteries. Int. J. Heat Mass Transf. 2021, 179, 121747. [Google Scholar] [CrossRef]
- Pan, L.; Sun, J.; Qi, H.; Han, M.; Chen, L.; Xu, J.; Wei, L.; Zhao, T. Along-Flow-Path Gradient Flow Field Enabling Uniform Distributions of Reactants for Redox Flow Batteries. J. Power Sources 2023, 570, 233012. [Google Scholar] [CrossRef]
- Jyothi Latha, T.; Jayanti, S. Ex-Situ Experimental Studies on Serpentine Flow Field Design for Redox Flow Battery Systems. J. Power Sources 2014, 248, 140–146. [Google Scholar] [CrossRef]
- Hsieh, C.; Tsai, P.; Hsu, N.; Chen, Y. Effect of Compression Ratio of Graphite Felts on the Performance of an All-Vanadium Redox Flow Battery. Energies 2019, 12, 313. [Google Scholar] [CrossRef]
- Maurya, S.; Nguyen, P.T.; Kim, Y.S.; Kang, Q.; Mukundan, R. Effect of Flow Field Geometry on Operating Current Density, Capacity and Performance of Vanadium Redox Flow Battery. J. Power Sources 2018, 404, 20–27. [Google Scholar] [CrossRef]
- Ma, X.; Zhang, H.; Xing, F. A Three-Dimensional Model for Negative Half Cell of the Vanadium Redox Flow Battery. Electrochim. Acta 2011, 58, 238–246. [Google Scholar] [CrossRef]
























| Compression Type | Flow Field Configuration | |||
|---|---|---|---|---|
| Conventional | Serpentine | Parallel | Interdigitated | |
| Uncompressed | √ | √ | √ | √ |
| Homogeneously compressed | √ | √ | √ | √ |
| Non-homogeneously compressed | * | √ | √ | √ |
| Term | Positive Electrode | Negative Electrode |
|---|---|---|
| , | - | /F |
| , | - | −/F |
| , | /F | - |
| , | −/F | - |
| , | −2/F | - |
| Electrode | Reaction | Oxidation State of Vanadium | Ionic Species in the Electrolyte |
|---|---|---|---|
| Negative | (charging) | (III) | H+, , , V3+, V2+ |
| (discharging) | (II) | ||
| Positive | (charging) | (IV) | VO2+, H+, , , VO2+, VO2+ |
| (discharging) | (V) |
| Boundary Condition Description | Condition |
|---|---|
| Velocity at the inlet and pressure at the outlet channel (Neumann condition) given for conservation of momentum. | |
| Flux condition for the porous electrode’s potential distribution along the electrode/current collector contact surface. Zero flux condition for all other surfaces of the electrode. | |
| Flux condition for electrolyte’s potential distribution along electrode/membrane contact surface. Insulation for other parts of the electrode. | |
| The expression for concentration of reactant species at any SOC in the inflow of inlet channel of both the electrodes. Concentration of vanadium ions at inlet are constant for given SOC. | |
| Diffusive fluxes are set to zero at the outlet of outflow channel (fully developed flow). | |
| There is no flux across all other boundaries of electrode and channel (set to wall condition). | |
| Current density in the membrane and electrolyte are equal. | |
| From Faraday’s law, proton flux is proportional to current. | |
| The relationship between the potentials and the concentrations is given by: |
| Zone | Properties | Type | ||
|---|---|---|---|---|
| Uncompressed | Non-Homogeneously Compressed | Homogeneously Compressed | ||
| Electrode under Rib | Porosity | 0.91 | 0.57 | 0.57 |
| Permeability (m2) | 6.733 × 10−9 | 2.935 × 10−11 | 2.935 × 10−11 | |
| Electrode under Channel | Porosity | 0.91 | 0.66 | 0.57 |
| Permeability (m2) | 6.733 × 10−9 | 7.43 × 10−11 | 2.935 × 10−11 | |
| Parameters | Values | Unit |
|---|---|---|
| V2+ diffusion coefficient | 2.4 × 10−10 | [m2.s−1] |
| V3+ diffusion coefficient | 2.4 × 10−10 | [m2.s−1] |
| VO2+ diffusion coefficient | 3.9 × 10−10 | [m2.s−1] |
| VO2+ diffusion coefficient | 3.9 × 10−10 | [m2.s−1] |
| H+ diffusion coefficient | 9.312 × 10−9 | [m2.s−1] |
| SO42− diffusion coefficient | 1.065 × 10−9 | [m2.s−1] |
| HSO4− diffusion coefficient | 1.33 × 10−9 | [m2.s−1] |
| Electrode conductivity | 500 | [S.m−1] |
| Electrode porosity | 0.91 | - |
| Electrode specific area | 1.62 × 104 | [m2.m−3] |
| Standard potential, positive reaction | 1.004 | [V] |
| Rate constant, positive reaction | 6.8 × 10−7 | [m.s−1] |
| Transfer coefficient, positive reaction | 0.55 | - |
| Standard potential, negative reaction | −0.255 | [V] |
| Dynamic viscosity | 4.928 × 10−3 | [Pa.s] |
| Rate constant, negative reaction | 1.7 × 10−7 | [m.s−1] |
| Transfer coefficient, negative reaction | 0.45 | |
| Dissociation constant | 0.25 | |
| HSO4− dissociation rate constant | 1 × 104 | [mol.m−3 s] |
| Membrane proton concentration | 1990 | [mol.m−3] |
| Membrane conductivity | 10 | [S.m−1] |
| V2+ initial concentration | 1280 | [mol.m−3] |
| V3+ initial concentration | 320 | [mol.m−3] |
| VO2+ initial concentration | 320 | [mol.m−3] |
| VO2+ initial concentration | 1280 | [mol.m−3] |
| H+ initial concentration, negative electrode | 4000 | [mol.m−3] |
| H+ initial concentration, positive electrode | 4000 | [mol.m−3] |
| HSO4− initial concentration, negative electrode | 4500 | [mol.m−3] |
| HSO4− initial concentration, positive electrode | 4500 | [mol.m−3] |
| Density | 1354 | [kg.m−3] |
| Flow rate | 40 | [mL.min−1] |
| Outlet pressure | 1 | Atm |
| Average current density | 60 | [mA.cm−2] |
| Cell temperature | 293.15 | [K] |
| SOC | 0.8 | - |
| Cell height | 0.05 | [m] |
| Cell depth | 0.05 | [m] |
| Electrode thickness | 0.003 | [m] |
| Membrane thickness | 0.0002 | [m] |
| Flow field thickness | 0.002 | [m] |
| Flow field width | 0.0053 | [m] |
| Compression Condition | Flow Field | Average Charging Voltage | Average Discharging Voltage |
|---|---|---|---|
| Uncompressed electrode | Conventional | 1.4044 | 1.2857 |
| Parallel | 1.3941 | 1.2956 | |
| Serpentine | 1.3801 | 1.3106 | |
| Interdigitated | 1.3647 | 1.3231 | |
| Non-homogeneously compressed electrode | Parallel | 1.393 | 1.3039 |
| Serpentine | 1.3867 | 1.3136 | |
| Interdigitated | 1.3777 | 1.3224 | |
| Compressed electrode | Conventional | 1.4392 | 1.2486 |
| Parallel | 1.4120 | 1.2728 | |
| Serpentine | 1.4006 | 1.2932 | |
| Interdigitated | 1.3922 | 1.3019 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saha, S.; Maniam, K.K.; Paul, S.; Patnaikuni, V.S. Hydrodynamic and Electrochemical Analysis of Compression and Flow Field Designs in Vanadium Redox Flow Batteries. Energies 2023, 16, 6311. https://doi.org/10.3390/en16176311
Saha S, Maniam KK, Paul S, Patnaikuni VS. Hydrodynamic and Electrochemical Analysis of Compression and Flow Field Designs in Vanadium Redox Flow Batteries. Energies. 2023; 16(17):6311. https://doi.org/10.3390/en16176311
Chicago/Turabian StyleSaha, Snigdha, Kranthi Kumar Maniam, Shiladitya Paul, and Venkata Suresh Patnaikuni. 2023. "Hydrodynamic and Electrochemical Analysis of Compression and Flow Field Designs in Vanadium Redox Flow Batteries" Energies 16, no. 17: 6311. https://doi.org/10.3390/en16176311
APA StyleSaha, S., Maniam, K. K., Paul, S., & Patnaikuni, V. S. (2023). Hydrodynamic and Electrochemical Analysis of Compression and Flow Field Designs in Vanadium Redox Flow Batteries. Energies, 16(17), 6311. https://doi.org/10.3390/en16176311