Load-Following Operation of Small Modular Reactors under Unit Commitment Planning with Various Photovoltaic System Conditions

Abstract

Globally, renewable energies are indispensable resources on account of RE100 and the Paris Agreement. The most developed renewable energies are photovoltaics (PV) and wind energy, and they are continuously expanding. This study aims to optimize and analyze the nuclear power plant (NPP) load-following operation in various PV conditions in a metropolitan region. With theoretically estimated power demand and PV power, a mixed-integer problem (MIP) with ramping cycle constraint (RCC) was constructed for a safe load-following operation and simulated through duck curves under various NPP load-following regions (the extreme, normal, and safe regions). The simulation showed two major results for NPP load-following. Technically, RCC successfully controlled the NPP ramp cycle and was assured to be an optimization tool for NPP operation. Numerically, NPP load-following alleviated PV intermittency to almost 50%, 30%, and 15% depending on the load-following region. However, these effects were restricted when the PV capacity rate was high, especially when it exceeded 60%. Thus, PV system capacity is recommended to be 63% of the maximum power demand in the metropolitan region with NPP load-following, and larger PV systems need more flexibility.

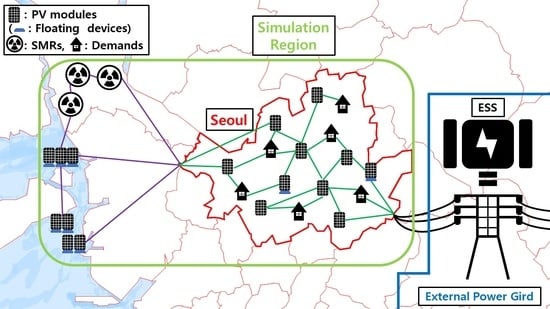
1. Introduction

The concept of the duck curve was first introduced in the California Independent System Operator (CAISO). The demand power curve reflected by renewable energies, which are noncontrollable, looks like a duck, so it is called the duck curve or power netload [1]. The power netload is increasingly important, since there is rapid power change arising from the intermittency of renewable energies. Currently, the global renewable energy power portion has just passed over 10% [2] and a power valley problem has been encountered.

The major component of renewable energy is the photovoltaic (PV) system. The PV power density is increasing year by year [3]. The PV system is intermittent because it generates power only in the daytime and is also critically influenced by the weather. There are many types of PV systems other than the conventional land PV system, such as floating PV (FPV) and marine PV (MPV) systems. FPV systems have additional advantages, such as installation surface limitations and a cooling effect [4]. Therefore, their capacity is continually increasing [5]. MPV systems, one of the FPV systems, are economically comparable with other offshore renewable energies, with high space availability [6]. Due to FPV’s huge potential, FPV systems play a key role in clean energy as they could avoid conflicts with other industries and generate more power than land PV [7].

Many studies have been conducted to increase the power density of PV systems. Currently, tunnel oxide passivated contact (TOPCon) is becoming a major technology to raise cell efficiency and power [8]. The high-density modules, such as the bifacial modules, are mounted on the FPV system to increase power since the bifacial FPV module can generate more power than the mono-facial FPV module, especially in the morning and evening [9]. The bifacial FPV system with east–west configuration generates more power than the south configuration because it makes it possible to install more PV modules per area, while it diminishes the heat loss coefficient as well [10,11]. Many studies have been conducted on increasing the power density of PV systems. However, the duck curve deepens as the PV power density increases, and more power grid flexibility is needed.

Non-dispatchable generators such as nuclear power plants (NPPs) need to be operated flexibly since renewable energy intermittency has been increased and dispatchable generators are not readily flexible due to economic reasons [12]. NPP load-following is one of the solutions to cope with these challenges. As France generates their electricity mostly with nuclear energy, the daily fluctuation of nuclear power is typically 5~10%, and sometimes more than 20% [13]. Germany, Belgium, Finland Switzerland, and Hungary also operate loads based on their own needs [14]. Additionally, the small modular reactor (SMR) plays the key role in load-following because of its own modularity [15]. SMRs that cogenerate hydrogen have been evaluated economically, and alkaline water electrolysis has been identified as the most profitable process for hydrogen cogeneration [16].

The NPP load-following model is being continuously studied. The mechanical Shim control strategy was applied to CPR1000 with a typical load-following scenario, the “12-3-6-3”, and the feasibility of the load-following was demonstrated [17]. Functional variable universe fuzzy PID control and the nonlinear controller can be utilized at different power levels to operate the proper load-following [18,19]. As these models deal with real NPP physical properties, there is no risk of NPP operation, and a compact NPP operation is possible. Particularly, one model utilized the balance of the plant system of CPR1000 and described very compact NPP parameter responses during load-following [17]. An aggregative model with a triangle membership function has been adapted and resulted in better precision load-following in view of coolant temperatures with less equations than the previous study [18]. A non-linear controller with 100 MWe PWR was used and described with influences depending on the load-following method (reactor-following and turbine-following) in view of the reactivity margin [19]. However, these models are hardly used in the power grid operation because of their large scale and complexity. It is hard for the system operators (SO) to check NPP parameters one-by-one.

The Unit Commitment (UC) plan is the representative tool to handle the power grid problem [20]. Compared to previous works [17,18,19], the UC plan decides NPP operations roughly but efficiently. Based on the “12-3-6-3” scenario, NPP with wind generation can be modeled with the optimization problem [21]. The models in [22,23] consider NPP as having very compact constraints, such as the flexibility constraint and the xenon-poisoning constraint. However, the typical “12-3-6-3” scenario has a weak point that is not suitable for the duck curve, and a refined “12-3-6-3” scenario for renewable energies is needed. This paper suggests a numerical analysis of the refined “12-3-6-3” scenario for PV systems.

In consideration of the NPP load-following operation, the ramping cycle (RC) is also crucial since it has a direct connection to the lifespan of the NPP. The RC is one cycle of NPP power when the power output first ramps down to the minimum from the initial level, and then returns to the initial level. The RC is designed to limit the load cycle with respect to the minimum power [13]. In general, the RC is designed for 2 times per day, 5 times per week, and 200 times per year. This limit is a natural result because NPP ramping typically results in pellet-clad mechanical interaction or xenon-poisoning [12,13,24].

In this paper, the NPP load-following scenario under a metropolitan power grid with a new optimization constraint, the ramping cycle constraint (RCC), is proposed. The simulation model is based on three types of NPP state variables describing the NPP operation with a nuclear flexibility constraint [22]. The nuclear flexibility constraint is used differently according to the NPP minimum power [23]. Finally, this paper shows the necessity of a refined “12-3-6-3” transition and the load-smoothing effect of NPP load-following in a metropolitan region.

The remainder of this paper is organized as follows. In Section 2, the process of collecting data, particularly power demand and PV power data, is described. In Section 3, the mathematical model composed of the UC plan and RCC is presented. In Section 4, the results of simulations in terms of RCC and load variability are described. Lastly, Section 5 provides an analysis of the proposed NPP load-following model and potential avenues for future works.

2. Data Acquisition

The data, including the power demand and PV power density, are essential in simulations. The power demand was assessed from the electricity usage of Seoul in 2021 and the relative power consumption coefficient of South Korea.

Table 1. Electricity consumption by use in 2021 in metropolitan Seoul [25].

Category	Use	Power Consumption (MWh)	Use	Power Consumption (MWh)
Dwelling	Dwelling	14,656,127	-	-
Service	General service	27,499,011	Public service	3,575,378
Industry (Manufacture)	Clothes, Fur	310,226	Transport devices	19,758
	Food	229,770	Electric devices	19,253
	Printing media	204,727	Agriculture, Fishery	19,189
	Other machinery	136,043	Vehicles	16,930
	Textile goods	108,992	Medicine	16,638
	Other products	107,280	Drinks	15,592
	Electronic, Mobile	62,799	Primary metals	12,425
	Metal processing	51,333	Wooden	4201
	Plastic	49,867	Furniture	3520
	Optical instrument	43,783	Briquette, Oil	3193
	Chemistry	42,368	Mining	1902
	Pulp, Paper	37,773	Industry machine	1343
	Non-metal	24,756	Cigarette	88
	Leather, Bag	21,502

lists the electricity usage of Seoul in 2021 [25]. The total electricity usage was 47,295,807 MWh. The dwelling usage was about 31% of the total electricity usage, while the service usage was about 66%, and the industry usage was the remaining 3%.

The relative power consumption coefficient provides the hourly average deviation of the power consumption, and the coefficients are calculated by Equations (1)–(3) [26]:

$$A_{i,t}=\frac{\sum _{k=1}^{M}H{P}_{i,k,t}}{M}$$

(1)

$$B_i=\frac{\sum _{t=1}^{24}{A}_{i,t}}{24}$$

(2)

$$C_{i,t}=\frac{A_{i,t}}{B_i}$$

(3)

where $i$ is the usage, $k$ is the day, and $M$ is the number of days in a month. $H{P}_{i,k,t}$ is the hourly power consumption in a day by use. $A_{i,t}$ is the daily average power consumption by hour and use. Then, $B_i$ is the hourly average power consumption by use. Finally, the relative power consumption coefficient, $C_{i,t}$, is calculated by dividing $A_t$ with $B$. If the coefficient is less than one, the power consumption is lower than the average power consumption. If the coefficient is greater than one, the power consumption is greater than the average power consumption.

Figure 1 shows the hourly average relative power consumption coefficient for the categories listed in Table 1. The dwelling coefficient was at its maximum in the evening, at 1.36, and at its minimum at dawn, at 0.73. The service and industry coefficients reached their peak values in the daytime, 1.36 and 1.28, respectively, although they exhibited different trends in the daytime. The hourly power demand, which is expressed by Equation (4), was obtained by multiplying the relative power consumption coefficient and the hourly average power consumption, as:

$$D_t=\sum _i{C}_{i,t}\times \frac{A{P}_i}{8760}$$

(4)

where $D_t$ is the hourly power demand, $C_{i,t}$ is the relative power consumption coefficient by usage, and $A{P}_i$ is the annual electricity consumption by usage. To obtain the hourly average power consumption, the annual electricity consumption was divided by 8760. The hourly power demand per month is shown in Figure 2a. The virtual electricity demand of Seoul had a huge gap of almost 3300 MW between the daytime and the nighttime demand. As Seoul is a downtown area, there is low electricity usage at night, so it is reasonable that a large gap in demand was observed.

A simple PV power prediction model expressed in (5) was used to predict the PV power. Many precise prediction models using either the regression analysis or artificial intelligence exist. The authors of [27] present various regression models, and the mean absolute percent error of those models is almost 6%. The authors of [28] present the short-term PV prediction based on a recurrent neural network, and its maximum accuracy is 99.1% (normalized mean absolute error). They required the various environmental hourly data, such as the relative humidity, wind speed, and ambient temperature, in common, which are hard to obtain without sensors.

$${PV}_t=P_R\times \frac{POA}{1000\left[\mathrm{W}/{\mathrm{m}}^2\right]}\times \left\{1+b\left(T_m-25\left[℃\right]\right)\right\}$$

(5)

where $P{V}_t$ is the hourly PV power, $POA$ is the plane of array irradiation, $P_R$ is the rated PV power, and $b$ is the temperature coefficient tested in standard test condition (STC, Solar Irradiance of 1000 (W/m²), module temperature of 25 $\mathrm{℃}$, and air mass of 1.5). Information about the test module used in the study is listed in

Table 2. Information about the PV modules used in the simulation.

Type of Module	${\mathit{P}}_{\mathit{R}}$ (Wp)	$\mathit{b}$$(\%/\mathbf{℃}$)
Si-Mono (Solar Park LCHD G1 series)	430	−0.42

.

The $POA$ was calculated by the geometric radiation model [29]. The solar constant, longitude, latitude, slope, and azimuth angle were 1367 W/m², 126° E, 37° N, 30°, and 0°, respectively. Extraterrestrial radiation was calculated first, then the effect of atmosphere in clear sky was applied with the direct and diffuse radiation models [30,31]. Figure 2b shows the $POA$ of clear sky in Seoul.

The module temperature, $T_m$, was calculated by the simple energy balance model [32]. This model needs various parameters, such as the heat exchange coefficient, STC module efficiency, temperature coefficient, absorption coefficient, transmittance of module cover, solar irradiation, and the hourly ambient temperature. Except for the value of the ambient temperature, the values of the other parameters were obtained from [32,33]. The hourly ambient temperature was calculated by the synthesizing sequence model using the monthly average minimum, maximum, and mean ambient temperatures in Seoul in 2021 [34,35]. Figure 2c shows the result of the module temperature calculation. Finally, the output of Equation (5) is presented in Figure 2d.

A simulation was conducted with various PV capacities. The PV capacity was set from 10% to 90% (10% interval) of the maximum power demand per month. It was assumed that the PV system always has the same power generation pattern regardless of PV system properties. Thus, PV system power could be calculated by the linear multiplication of $P{V}_t$ and the power netload is calculated by (6), as:

$${ND}_t=D_t-R\times \frac{P{V}_t}{430\left[Wp\right]}$$

(6)

where $N{D}_t$ is the hourly power netload and $R$ is the PV system capacity. Figure 3 shows the partial results of Equation (6).

3. Mathematical Model Simulation

The UC plan is a rough schedule of generation units based on power demand prediction, formulated as a mixed-integer problem (MIP). The integer variables are particularly useful as they can easily represent the state of the generated unit, which is either ON or OFF. An efficient NPP model could be obtained from a literature [22]. Three state variables (ON, OFF, STABLE) make NPP ensure the minimum stable time by constructing dimensional optimization constraints. In this paper, Reference [22] was used as the base model, and RCC for the safe NPP load-following scenario was added to it. The simulation location is the downtown area of Seoul, where many PV systems are already installed. NPP and the energy storage system (ESS) were considered as the power source to evaluate the effect of NPP load-following through simulation. The ESS is considered as an external power grid in this study. The ESS has limitless capacity and takes charge of the residual of the power netload. Thus, the objective function of MIP is maximizing the NPP power for NPP economics.

3.1. Simulation of the Base Model

Simulations were run by MATLAB 2022b and its Optimization toolbox. The MIP nomenclatures used in [22] were easily distinguishable from the original feature. Equations (7) to (11) show the basic constraints of the NPP. However, some of these constraints differed from the original ones.

$$PMI{N}_{d,j}\le p_{t,j}\le PMA{X}_j$$

(7)

$$p_{t-1,j}-p_{t,j}\le R{D}_j\times R{d}_{t,j}-\delta \times U{p}_{t,j}$$

(8)

$$p_{t,j}-p_{t-1,j}\le {RU}_j\times {Up}_{t,j}-\delta \times {Rd}_{t,j}$$

(9)

$$R{d}_{t,j}+U{p}_{t,j}+S{t}_{t,j}==1$$

(10)

$$\left(U{p}_{t,j}-U{p}_{t-1,j}\right)\times PMINSTABL{E}_{d,j}\le {\sum }_{tt=t-PMINSTABL{E}_{d,j}}^{t-1}(S{t}_{t,j}+U{p}_{t,j})$$

(11)

The nuclear power is limited from $PMI{N}_{d,j}$ to $PMA{X}_j$, as seen in (7). The operative reserve was not considered. Equations (8) and (9) demonstrate ramping of nuclear power, which are limited by $R{D}_j$ and $R{U}_j$. The auxiliary constant, $\delta$, exists to distinguish $St$ states ($p_{t-1,j}=p_{t,j}$). Equation (10) represents the complementary constraint in state variables $Rd$, $Up$, and $St$. Equation (11) represents the flexibility constraint after down-ramping to handle xenon-poisoning.

$$\left({Rd}_{t,j}-{Rd}_{t-1,j}\right)\times PMAXSTABL{E}_{d,j}\le {\sum }_{tt=t-PMAXSTABL{E}_{d,j}}^{t-1}(S{t}_{t,j}+{Rd}_{t,j})$$

(12)

$${\sum }_j{p}_{t,j}+ESS==N{D}_t$$

(13)

$${\sum }_j{p}_{t,j}\le L{D}_t$$

(14)

In this study, additional constraints on the NPP load were imposed, as shown in Equations (12)–(14). Equation (12) outlines the flexibility constraint after up-ramping to handle xenon-poisoning, and Equation (11) is the opposite. Similar to the down-ramping, up-ramping of the NPP also induces xenon-poisoning and requires stabilization time after up-ramping [36]. Equation (13) represents the power balance constraint equation. The other generation units are considered as $ESS$ in this paper. Equation (14) represents the load-following constraint and $L{D}_t$ is the hourly load-following scenario.

$$L{D}_t=N{D}_t-\min \left(N{D}_t\right)+{PMIN}_{d,j}$$

(15)

Load-following reduces the risk of sudden ramping of the baseload plant and the load variability. $N{D}_t$ is the power netload, and the load-following scenario is performed using these values. $L{D}_t$ must be bigger than $PMI{N}_{d,j}$, as expressed in Equation (15). Some examples of the load-following scenarios are “12-3-6-3” and “(2-10)-2-(10-18)-2” [21]. Figure 4 shows schematics of load-following scenarios. The upper plot shows the “12-3-6-3” scenario, where NPP operates at minimum power for 12 h during the night, ramps up for 3 h, operates at maximum power for 6 h during the day, and then ramps down for 3 h.

The lower plot of Figure 4 shows a more flexible NPP operation, which is “(2-10)-2-(10-18)-2”. Although the fundamental structure of the scenario is the same as the upper plot, NPP ramps faster and the stable time after ramping is not fixed. This is depicted by the dotted line. However, faster ramping critically impacts the NPP lifespan. Additionally, the stable time is proportional to the size of the power ramping at once, and it is dependent. Both scenarios were used to model the general power demand without renewable energies. Therefore, a refined load-following scenario is needed.

3.2. Ramping Cycle Constraint

In this paper, a new constraint was added, RCC. The NPP was designed to limit the RC regarding the minimum power. The RCC is based on “per day”, as expressed in Equations (16)–(19):

$$\left(U{p}_{t,j}-S{t}_{t,j}\right)-\left(U{p}_{t-1,j}-S{t}_{t-1,j}\right)-1\le RU{S}_{t,j}$$

(16)

$$RU{S}_{t,j}\le U{p}_{t,j}$$

(17)

$$RU{S}_{t,j}\le {St}_{t-1,j}$$

(18)

$$\sum _{t}RU{S}_{t,j}\le R{C}_j$$

(19)

Equation (16) is used to detect the starting point of ramping-up. $RU{S}_{t,j}$ is a binary variable and becomes 1 when NPP ramp-up starts.

Table 3. All the numbers of cases in Equation (16).

Index	$\mathit{U}{\mathit{p}}_{\mathit{t},\mathit{j}}$	$\mathit{S}{\mathit{t}}_{\mathit{t},\mathit{j}}$	Index	$\mathit{U}{\mathit{p}}_{\mathit{t}-1,\mathit{j}}$	$\mathit{S}{\mathit{t}}_{\mathit{t}-1,\mathit{j}}$
①	1	0	④	1	0
②	0	1	⑤	0	1
③	0	0	⑥	0	0

shows all cases described by Equation (16). Not all state variables can be 1 because of Equation (10). Due to Equations (11) and (12), state variables $Up$ and $Rd$ do not exist continuously. The ramping-up starting point is detected by matching “①–⑤”. As a result of Equation (16), the left side of the equation has the following discrete values: 1 in case “①–⑤”, 0 in cases “①–⑥” and “③–⑤”, –1 in cases “①–④”, “②–⑤”, and “③–⑥”, –2 in cases “②–⑥” and “③–④”, and –3 in case “②–④”. The value of $RU{S}_{t,j}$ is set to 1 at the ramping-up starting point but it must be restricted at the other points by the inequality sign, as expressed in Equations (17) and (18). In other cases, either $U{p}_{t,j}$ or $S{t}_{t-1,j}$ is 0. All $RU{S}_{t,j}$ except for “①–⑤” are 0. The total ramping-up start point is limited by Equation (19). $R{C}_j$ represents the daily load cycle of the $j^{th}$ NPP, which is equivalent to “one cycle per day”.

Equations (20)–(23) were used to detect the ramping-down start point:

$$\left({Rd}_{t,j}-S{t}_{t,j}\right)-\left({Rd}_{t-1,j}-S{t}_{t-1,j}\right)-1\le RD{S}_{t,j}$$

(20)

$$RD{S}_{t,j}\le {Rd}_{t,j}$$

(21)

$$RD{S}_{t,j}\le {St}_{t-1,j}$$

(22)

$$\sum _{t}RD{S}_{t,j}\le R{C}_j$$

(23)

where $RD{S}_{t,j}$ is the binary variable and detects the ramping-down start point. Since there must be an end if there is a beginning, the end point detection is not necessary.

4. Results

In this section, the netload deviation of residual power is evaluated, and the effectiveness of the reactor in load-following is analyzed. Two types of simulations were conducted, the RCC and SMR simulations. The specific simulation settings are listed in

Table 4. Values used in the simulations.

Constant	Value	Reference
$P_r$ (MW)	$335,1000$	-
$PMIN$ (MW)	$0.2\times P_r$, $0.5\times P_r$, $0.7\times P_r$	[13]
$PMAX$ (MW)	$P_r$	-
$\delta$ (-)	0.0001	[22]
$RD$ (MW/min)	$0.005\times P_r$	[13]
$RU$ (MW/min)	$0.005\times P_r$	[13]
$PMINSTABLE$ (hour)	$6,3,1$	[22,23]
$PMAXSTABLE$ (hour)	$1$	[22]
$RC$ (cycle/day)	$1$	[13]

. $P_r$ is the NPP rated power and it was set as 1000 MW in the RCC simulation and 355 MW in the SMR simulation. $PMI{N}_{d,j}$ was divided into three parts: the safe following region (70% of $P_r$), the normal following region (50% of $P_r$), and the extreme following region (20% of $P_r$). $R{D}_j$ and $R{U}_j$ are the NPP ramping rates per minute and were set to 0.5% of $P_r$ for secure NPP operation [13]. $PMINSTABLE$ had three values regarding the xenon-poisoning constraint for the realistic simulation [23].

4.1. RCC Simulation

RCC simulation was conducted with two 1000 MW NPPs to determine the impact of the RCC. Consequently, RCC effectively controlled the RC, as shown in Figure 5. $LD$ in Figure 5 is the load-following constraint. Figure 5a is the result of the simulation without the RCC in the normal following region. NPP #1 and #2 have two ramping start points to follow $LD$, a ramping-up start point and a ramping-down start point. In Figure 5a, the total NPP power was to be 40,747 MWh, which was 7253 MWh lower than that of the baseload. Figure 5b is the result of the simulation with the RCC, and the total NPP power was set to be 39,158 MWh, which was 8842 MWh lower than the baseload. The RC was limited by RCC and had only one start point. Although, the RCC reduced the NPP operation power by almost 1000 MW in this case, and the safe NPP load-following was possible.

4.2. SMR Simulation

SMR simulation, used to evaluate the NPP load-following effect, is composed of two stages: the load-following stage and the load-variability stage. An SMR of 335 MW was chosen in this simulation since it is reasonable to build such SMR in metropolitan regions because of its simplicity and enhanced safety [37]. The total SMR capacity is limited to 30% of the maximum power netload since the Korean government restricted the NPP generation rate to 30%. In the load-following stage, the transition of “12-3-6-3”, depending on PV system capacity by analyzing one 335 MW SMR simulation, was described. In the load-variability stage, the SMR simulation in power netload was applied to verify how NPP load-following affects the metropolitan region.

4.2.1. The Load-Following Stage

There was a significant change in the NPP load-following scenario with the PV system. Figure 6 shows the average result of the extreme following region regrading PV capacity. Each subfigure has two plots, the upper is the top view and the lower is the entire view. The color in plots shows the SMR power: yellow means 335 MW (maximum), blue means 67 MW (minimum), and purple shows the ramping region. Figure 6a shows the typical “12-3-6-3” scenario with ramping starting at 0 and 6 o’clock. With an increase in the PV capacity, the blue region moves from night to daytime, as can be seen in Figure 6b,c. Finally, the blue region settles down at 8 to 13 o’clock, which is the time when PV power is generated, as can be seen in Figure 6d.

The average ramping region (purple), depending on PV capacity, is organized in

Table 5. Average ramping region hours.

PV	Extreme Following Region		Normal Following Region		Safe Following Region
	Ramping-Down (h)	Ramping-Up (h)	Ramping-Down (h)	Ramping-Up (h)	Ramping-Down (h)	Ramping-Up (h)
10%	23.334	7.209	1.084	7.042	2.875	6.333
20%	23.292	8.709	1.021	7.167	2.875	6.646
30%	23.334	9.750	1.230	8.021	2.855	6.750
40%	23.229	10.688	1.250	10.042	2.855	7.980
50%	23.500	11.938	2.729	11.833	4.063	11.021
60%	2.104	14.625	5.792	14.188	7.709	13.813
70%	4.479	15.083	7.688	14.604	10.229	13.958
80%	5.521	15.375	9.563	14.875	11.271	14.042
90%	6.688	15.792	9.875	14.958	11.396	14.042

. “Ramping-down” and “ramping-up” are the average durations of the ramping-down and ramping-up regions, respectively. The average duration of the ramping-up region hour showed a similar trend regardless of load-following regions, increasing from 7 to 15 o’clock. In contrast, the average duration of the ramping-down region exhibited different trends in each following region owing to Equation (11). Sharp ramp-up and ramp-down changes were observed between 50% and 60% when the duck curve intensity was aligned with the lowest point of the power netload, an almost three-hour transition. Under a high PV system capacity, a revised “12-3-6-3” transition is needed for appropriate NPP load-following.

4.2.2. The Load-Variability Stage

Figure 7 shows the absolute deviation of the SMR, baseload operation, and load-following operation. The baseload operation requires continuously generating the maximum power of SMR. The deviation was calculated by subtracting the residual netload with the mean residual netload. The residual netload was also calculated by subtracting the power netload with the total SMR power. The upper plot of Figure 7 is a result for the baseload operation, and the plot below is a result for the load-following. At a low PV capacity, a high deviation was concentrated in the afternoon and at dawn, and successfully mitigated by SMR load-following, as can be seen in Figure 7a. When the PV capacity was increased, a high deviation was only concentrated in the afternoon, but it deepened owing to the PV and was weakly mitigated, as can be seen in Figure 7b,c. Under a high PV capacity, the high deviation appeared in the daytime and was hardly mitigated, especially in the afternoon, as can be seen in Figure 7d.

Table 6. Statistical analysis chart of the deviation.

PV	Baseload (MW)		Load-Following (MW)
			Extreme Following Region		Normal Following Region		Safe Following Region
	Max	Mean	Max	Mean	Max	Mean	Max	Mean
10%	1979	946	1269	451	1561	694	1680	833
20%	1885	835	1357	377	1658	581	1781	721
30%	1993	750	1438	358	1752	529	1882	645
40%	2153	737	1521	351	1889	514	2029	635
50%	2313	783	1544	367	1985	519	2165	650
60%	2473	860	1824	456	2102	621	2320	752
70%	2633	952	1893	581	2263	770	2467	890
80%	2793	1054	2556	723	2525	894	2671	1000
90%	2953	1166	3122	835	2727	1008	2863	1114

shows the numerical analysis of load variability. “Max” is the observed maximum deviation and “Mean” is the observed mean deviation. The value of Max indicates a peak-shaving effect [38]. The more the NPP operation region deepens, the more the peak-shaving effect appeared; however, it worsened with the increase of PV capacity.

Figure 8a shows the relative ratio of Max based on the baseload. A small relative ratio is indicative of a superior peak-shaving effect. The deterioration first appeared at 20%, when the duck curve started to deepen, and then at 72%, 88%, and 94% depending on the following regions. Superior deteriorations appeared after a 60% PV capacity rate. The relative ratios reached their maximum values, along with an increase of PV capacity, at 106%, 92%, and 97%.

The Mean tendency had a valley, unlike the Max tendency. The Mean decreased by 40% and increased after 50%, as shown in Table 6. Figure 8b shows the relative ratio of Mean based on the baseload. When the relative ratio is small, it shows a superior load-smoothing effect. Good load-smoothing effects were maintained until the PV capacity rate reached 60%. Similar to the Max, the Mean exhibited deteriorations after 60% PV capacity. Maximum values for the relative ratios were achieved, along with an increase of PV capacity, at 72%, 86%, and 96%. By assuming that deterioration started as 3% above the Mean relative ratio at a 10% PV capacity rate, we could determine the PV capacity rates where the load-following effects are still effective depending on the load-following region using a linear approximation. These rates were: 57.7%, 65.2%, and 66.1%. Consequently, SMR load-following experienced a limitation after a 63% (mean value) PV capacity rate in the downtown region.

5. Conclusions

In this study, SMR modeling with the RCC in the UC plan was proposed and the effect of SMR load-following under various duck curves in the metropolitan region of Seoul was analyzed. The 335 MWe SMRs were considered in this study, but other sizes of SMRs (100~500 MWe) could also be sufficiently considered with the suggested model. Different simulations for multiple purposes can be run by increasing the size of RC or by changing the equality constraint under conditions where renewable energy is utilized. Under “one per day”, the transition of the NPP typical load-following scenario was observed as “12-3-6-3”. The simulation results presented the necessity of a time shift from dawn to daytime in the “12-3-6-3” scenario depending on the size of the PV system.

Additionally, the peak-shaving and load-smoothing effects of SMR load-following in the downtown region were evaluated. SMR alleviated the deviation of power netload by almost 50%, 30%, and 15%, in proportion to the size of the load-following regions. However, these effects started to deteriorate after the PV capacity rate of 60%. Load-smoothing effects were diminished to halves under higher capacity rates of the PV systems. Consequently, the NPP and SMR should mitigate the impact of PV peak power by shifting the “12-3-6-3” scenario time. These mitigations worked sufficiently until the size of the PV system reached 60% of the maximum power demand. Thus, it is recommended that the size of the PV system in a metropolitan region would be able to meet 60% of the maximum power demand. If it is expected to meet a higher power demand, other considerations are needed.

However, there were some supplement points in the simulation. Owing to the auxiliary constant, $\delta$, the simulation had an undesirable ramping outcome. In Figure 5b, NPP #2 had an unintended longer ramp-up state. Furthermore, the simulation was assessed under an urban area, where the power demand had a huge gap, and the duck curve was weak. The typical “12-3-6-3” scenario reached its limit more quickly than in the proposed simulation when the general power demand had proper rates of power usage.

In future studies, the economic analysis of NPP and SMR load-following will be considered to determine their economic feasibility, as they have a large construction cost and a low power cost. Not only PV, but also wind power and other major renewable sources such as floating PV and marine PV, will be considered for a realistic SMR power plan. Although floating and marine PV are more affected by environmental factors than rooftop or land PV, especially owing to waves and powerful wind, this problem could be solved by designing floating bifacial PV with different installation azimuths [10]. In addition, the floating PV is suitable for metropolitan regions, which have low effective land availability [5]. With systemic methods, power demand–supply program research with floating PV will be considered to raise the stability of the power gird. The results of such research would inform the design of PV systems in downtown regions where there is insufficient land to install PV systems.

NPPs and SMRs are needed in the transitional power plant because of its lower power cost and carbon emissions compared to other power plants. In addition, the intermittency of renewable energies causes severe risks to the power grid system operator and the NPP baseload operation. In the near future, SMR could be connected with high-efficiency PV systems with high power density modules, such as bifacial and shingled structures made of TOPCON cells. The system would then be combined with different installation sites, such as floating and marine environments, and in the building for BIPV. Finally, this study could contribute to the optimal power planning of system operators to stabilize the power grid as a soft landing for the complete RE100.