Classification and Clustering of Electricity Demand Patterns in Industrial Parks
Abstract
:1. Introduction
2. System Architecture
- Historical Data: the database storing the consumption data by quarter-hours, including calendar information for each sample such as day, month, year, workability and day of the week.
- Data Pre-Processing: to clean the database (removing erroneous samples or interpolating, when possible, missing data) and accommodate the format to the input of the following examples (e.g., aggregating quarter-hour samples in hourly values).
- Outlier Detection: An implementation of the Principal Component Analysis (PCA) method to identify and remove erroneous data (produced for instance due to monitoring hardware malfunctions), discriminating them from proper data which shows abnormal values (such as a bank holiday, which normally presents an abnormal load curve).
- SOM + CLUSTERING: represents the combined application of SOM and k-means.
- Graphic Output: its main task is to send the information of the results given by the previous stage, to be displayed graphically.

2.1. Self-Organizing Map

2.2. Clustering
2.3. Combination of Algorithms
3. Case of Study
3.1. Research Data and Test Scenario

3.2. Configuration of Self-Organizing Map
- ▪
- Random: for each component xi, the values are distributed uniformly in the range of [min(xi),max(xi)].
- ▪
- Linear: eigenvalues and eigenvectors of the training data are calculated and then the map started along the largest eigenvectors of mdim, where mdim is the dimension of the network map.
- ▪
- Month (January = 1, February = 2…, November = 11, December = 12).
- ▪
- Day of the week (Sunday = 0, Monday = 1,…, Friday = 5, Saturday = 6).
- ▪
- Workability: holiday 1 and working day 2.
- ▪
- 24 values of hourly electricity consumption, representing the daily load curve.
3.3. Configuration of k-Means Algorithm
4. Results
4.1. Classification with Self-Organizing Map
- First, the clusters are shown in Figure 4 separated according the workability of the days. The left part of the image shows how non-working days were clustered, and the right part presents how working days were clustered.
- Figure 5 shows how the days of the different months were clustered. It is easy to see that January, February and March activate similar neurons; April, May, June and July also form a group of similar activations, as September, October and November do; August and December are both of them isolated. This makes sense, as seasons are roughly outlined, together with summer holidays (August) and Christmas (December). Electricity demand is seasonally dependent, as shown by Hernández et al. [27].
- Figure 6 presents how the different days of the week were clustered, resulting in four different patterns of activation: Mondays have their own activation pattern; Tuesday, Wednesday, Thursday and Friday have similar activation patterns; Saturdays and Sundays have again their own differentiated activation patterns.
- Finally, Figure 7 presents a combined analysis of clusters by day of the week and workability. All holidays are clustered around neurons similar to those of Sunday, except Wednesdays and Thursdays.




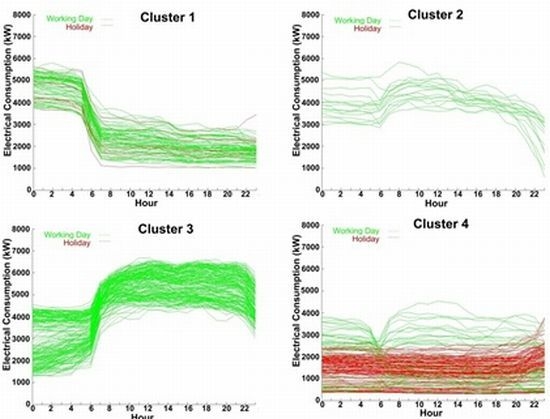
4.2. Clustering with k-Means

4.3. Decision Algorithm


| Number of cluster | Day of the week | Month | Workability | Average consumption (kW) |
|---|---|---|---|---|
| Cluster 1 | Saturday | Indifferent | Working Day | 4000 < Consumption |
| Saturday | Holiday | |||
| Cluster 2 | Indifferent | Indifferent | Working Day | 4000 |
| Cluster 3 | Tuesday | Not August | Working Day | 4000 < Consumption < 6000 |
| Wednesday | ||||
| Thursday | ||||
| Friday | ||||
| Cluster 4 | Monday | Indifferent | Working Day | 1500 < Consumption < 4500 |
| Tuesday | August | |||
| Wednesday | ||||
| Thursday | ||||
| Friday | ||||
| Cluster 5 | Monday | Indifferent | Holiday | Consumption < 4000 |
| Tuesday | ||||
| Wednesday | ||||
| Thursday | ||||
| Friday | ||||
| Saturday | ||||
| Sunday | ||||
| Saturday | Indifferent | Working Day | Consumption < 4000 |
5. Conclusions and Future Works
Acknowledgements
References
- Optimagrid: The Project Aims to Define, Design, Develop and Implement Intelligent Control Systems of Energy That Facilitate the Management Real-Time of a Microgrid. Available online: http://www.optimagrid.eu/ (accessed on 20 February 2012).
- Hingorani, N.G. Introducing custom power. IEEE Spectr. 1995, 32, 41–48. [Google Scholar] [CrossRef]
- Liserre, M.; Sauter, T.; Hung, J.Y. Future energy systems: Integrating renewable energy resources into smart power grid through industrial electronics. IEEE Ind. Electron. Mag. 2010, 4, 18–37. [Google Scholar] [CrossRef]
- Halpin, S.M.; Smith, J.W.; Litton, C.A. Designing industrial systems with a weak utility supply. IEEE Ind. Electron. Mag. 2001, 7, 63–70. [Google Scholar] [CrossRef]
- Xinghuo, Y.; Cecati, C.; Dillon, T.; Simoes, M.G. The new frontier of smart grids. IEEE Ind. Electron. Mag. 2011, 5, 49–63. [Google Scholar]
- Santacana, E.; Rackliffe, G.; Tang, L.; Feng, X. Getting smart. IEEE Power Energy Mag. 2010, 8, 41–48. [Google Scholar] [CrossRef]
- Park, J.-I. A smart factory operation method for a smart grid. In Proceedings of the 2010 40th International Conference on Computers and Industrial Engineering (CIE), Awaji City, Japan, 25–28 July 2010.
- Zareipoor, H.; Cañizares, C.A.; Bhattacharga, K. Economic impact of electricity market price forecasting errors: A demand-side analysis. IEEE Tran. Power Syst. 2010, 25, 254–262. [Google Scholar] [CrossRef]
- Vaccaro, A.; Popou, M.; Villacci, D.; Terzija, V. An integrated framework for smart microgrids modelling, monitoring, control, communication, and verification. Proc. IEEE 2011, 99, 119–132. [Google Scholar] [CrossRef]
- García, J.L.; Blasco, J.A.; del Brío, M.B.; Dominguez, J.A.; Barquillas, J.; Ramirez, I.J.; Medrano, N.J. Short-term electric power load-forecasting using artificial neural networks. Part I: Self-organizing networks for classification of day types. In Proceedings of the Fourteenth IASTED International Conference Modelling, Identification and Control, Igls, Austria, 20–22 February 1995; IASTED (International Association of Science and Technology for Development): Alberta, Canada, 1995; pp. 218–222. [Google Scholar]
- García, J.L.; Blasco, J.A.; del Brío, M.B.; Dominguez, J.A.; Barquillas, J.; Ramirez, I.J.; Medrano, N.J. Short-term electric load-forecasting using ANN. Part II: Multilayer perception for hourly electric-demand forecasting. In Proceedings of the Fourteenth IASTED International Conference Modelling, Identification and Control, Igls, Austria, 20–22 February 1995; IASTED (International Association of Science and Technology for Development): Alberta, Canada, 1995; pp. 223–227. [Google Scholar]
- Marín, F.J.; García-Lagos, F.; Joya, G.; Sandoval, F. Global model for short-term load forecasting using artificial neural networks. IEE Proc Gener. Transmi. Distrib. 2002, 149, 121–125. [Google Scholar] [CrossRef]
- Mori, H.; Itagaki, T. A precondition technique with reconstruction of data similarity based classification for short-term load forecasting. In Proceedings of 2004 IEEE Power Engineering Society General Meeting, Denver, CO, USA, 6–10 June 2004.
- Carpinteiro, O.A.S.; Reis, A.J.R. A SOM-based hierarchical model to short-term load forecasting. In Proceedings of 2005 IEEE Russia Power Tech, St. Petersburg, Russia, 27–30 June 2005.
- Wang, Z.Y. Development case-based reasoning system for short-term load forecasting. In Proceedings of 2006 IEEE Russia Power Engineering Society General Meeting, Montreal, Canada, 18–22 June 2006.
- George, T.J.; Hatziargyriou, N.D.; Dialynas, E.N. Two-stage pattern recognition of load curves for classification of electricity customers. IEEE Trans. Power Syst. 2007, 22, 1120–1128. [Google Scholar] [CrossRef]
- Chicco, G.; Napoli, R.; Piglione, F.; Postolache, P.; Scutariu, M.; Toader, C. Load pattern-based classification of electricity customers. IEEE Trans. Power Syst. 2004, 19, 1232–1239. [Google Scholar] [CrossRef]
- Kohonen, T. The Self-organizing Map. Proc. IEEE 1990, 78, 1464–1480. [Google Scholar] [CrossRef]
- Kohonen, T. Self-organized formation of topologically correct feature maps. Biol. Cybern. 1982, 43, 59–69. [Google Scholar] [CrossRef]
- Kohonen, T. Analysis of a simple self-organizing process. Biol. Cybern. 1982, 44, 135–140. [Google Scholar] [CrossRef]
- Kohonen, T. The neural phonetic typewriter. IEEE Comput. Mag. 1988, 21, 11–22. [Google Scholar] [CrossRef]
- MacQueen, J.B. Some methods for classification and analysis of multivariate observations. In Proceedings of the 5th Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, CA, USA, 18–21 July 1967; University of California Press: Berkeley, CA, USA, 1967; pp. 281–297. [Google Scholar]
- Vesanto, J.; Alhoniemi, E. Clustering of the self-organizing map. IEEE Trans. Neural Netw. 2000, 11, 586–600. [Google Scholar] [CrossRef] [PubMed]
- López, M.; Valero, S.; Senabre, C.; Aparicio, J. A SOM neural network approach to load forecasting. Meteorological and time frame influence. In Proceedings of the 2011 International Conference on Power Engineering and Electrical Drivers, Málaga, Spain, 11–13 May 2011.
- Hsu, Y.-Y.; Yang, C.-C. Design of artificial neural networks for short-term load forecasting. Part I: Self-organising feature maps for day type identification. IEE Proc. C Gener. Transm. Distrib. 1991, 138, 407–413. [Google Scholar]
- Davies, D.L.; Bouldin, D.W. A cluster separation measure. IEEE Trans. Pattern Anal. Mach. Intell. 1979, PAMI-1, 224–227. [Google Scholar]
- Hernández, L.; Baladrón, C.; Aguiar, J.M.; Calavia, L.; Carro, B.; Sánchez-Esguevillas, A.; Cook, D.J.; Chinarro, D.; Gómez, J. A study of the relationship between weather variables and electric power demand inside a smart grid/smart world framework. Sensors 2012, 12, 11571–11591. [Google Scholar] [CrossRef]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Hernández, L.; Baladrón, C.; Aguiar, J.M.; Carro, B.; Sánchez-Esguevillas, A. Classification and Clustering of Electricity Demand Patterns in Industrial Parks. Energies 2012, 5, 5215-5228. https://doi.org/10.3390/en5125215
Hernández L, Baladrón C, Aguiar JM, Carro B, Sánchez-Esguevillas A. Classification and Clustering of Electricity Demand Patterns in Industrial Parks. Energies. 2012; 5(12):5215-5228. https://doi.org/10.3390/en5125215
Chicago/Turabian StyleHernández, Luis, Carlos Baladrón, Javier M. Aguiar, Belén Carro, and Antonio Sánchez-Esguevillas. 2012. "Classification and Clustering of Electricity Demand Patterns in Industrial Parks" Energies 5, no. 12: 5215-5228. https://doi.org/10.3390/en5125215
APA StyleHernández, L., Baladrón, C., Aguiar, J. M., Carro, B., & Sánchez-Esguevillas, A. (2012). Classification and Clustering of Electricity Demand Patterns in Industrial Parks. Energies, 5(12), 5215-5228. https://doi.org/10.3390/en5125215