System Design and Analysis of a Directly Air-Assisted Turbocharged SI Engine with Camshaft Driven Valves

Abstract

The availability of compressed air in combination with downsizing and turbocharging is a promising approach to improve the fuel economy and the driveability of internal combustion engines. The compressed air is used to boost and start the engine. It is generated during deceleration phases by running the engine as a piston compressor. In this paper, a camshaft-driven valve is considered for the control of the air exchange between the tank and the combustion chamber. Such a valve system is cost-effective and robust. Each pneumatic engine mode is realized by a separate cam. The air mass transfer in each mode is analyzed. Special attention is paid to the tank pressure dependence. The air demand in the boost mode is found to increase with the tank pressure. However, the dependence on the tank pressure is small in the most relevant operating region. The air demand of the pneumatic start shows a piecewise continuous dependence on the tank pressure. Finally, a tank sizing method is proposed which uses a quasi-static simulation. It is applied to a compact class vehicle, for which a tank volume of less than 10 L is sufficient. A further reduction of the tank volume is limited by the specifications imposed on the pneumatic start.

1. Introduction

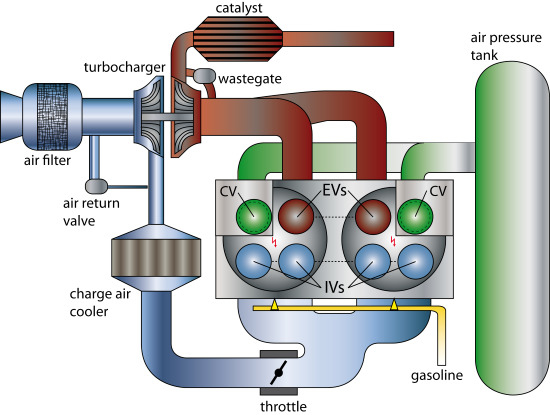
The use of compressed air to reduce the fuel consumption and improve the driveability of internal combustion engines has been extensively investigated for many years [1,2,3,4,5]. In a directly air-assisted engine, an additional air tank is directly connected to the combustion chamber. The air exchange is controlled with a designated valve, called charge valve (CV). A schematic of the resulting engine system is depicted in Figure 1.

Figure 1. Schematic of the directly air-assisted turbocharged SI engine: intake valve (IV), exhaust valve (EV) (Figure taken from [6]).

Figure 1. Schematic of the directly air-assisted turbocharged SI engine: intake valve (IV), exhaust valve (EV) (Figure taken from [6]).

The hybrid pneumatic engine (HPE) presented in [7] is one type of a directly air-assisted engine. Its architecture enables new engine modes. In the pneumatic start mode, compressed air is injected during the expansion stroke to start the engine. In [8] start times of less than 350 ms were reported, which is fast enough for stop-start applications. Thus, idling losses can be avoided. In the pneumatic motor mode, compressed air is also injected during the expansion stroke to drive the vehicle with compressed air only. In the boost mode, compressed air is injected during the compression stroke. The torque and the exhaust enthalpy are increased immediately. This mode is particularly useful for turbocharged (TC) engines because the turbo lag can be eliminated. The compressed air required to enable the modes described previously is generated during the vehicle deceleration, when the engine is operated as a piston compressor. In the so-called pump mode, the CV is opened towards the end of the compression stroke.

As described in [9], the common assumption initially was that all engine valves had to be fully variable. The authors of [10] proposed to only have a fully variable CV in order to reduce costs and complexity. With this configuration, fuel savings of 31% were achieved on the New European Drive Cycle (NEDC) [11]. Downsizing enabled by the boost mode contributed 25%, while the contributions of the stop/start capability and of the pneumatic motor mode each amounted to 3%.

A further reduction of costs and complexity can be achieved if a camshaft-driven CV is used as proposed in [6]. Each mode is then realized by a separate cam. A cam-shifting architecture as presented in [12] is used to change among the various cams. Consequently, the CV profile, which is defined by the opening instant, the closing instant, the valve lift, is fixed in each mode and needs to be carefully chosen. Cam design methodologies have been proposed for the boost mode [6] and the pneumatic start mode [13]. They cope with the various constraints, such as a lower limit for the tank pressure to prevent the flow of air–fuel mixture to the tank.

The limited variability of the camshaft driven-valve has an impact on the torque control. In the boost mode, the torque can be controlled by the ignition angle [14] by retarding the ignition angle if the amount of air–fuel mixture in the cylinder is too high. In the pump mode, the friction brakes are used to control the torque if the desired deceleration is larger than the power absorption of the pump mode. In the pneumatic start, the driver does not demand a particular torque, but wants to reach the idling speed as fast as possible. Hence, a precise torque control is not necessary. Finally, in the pneumatic motor mode, the torque is controlled by the valve timing [15]. This requirement cannot be fulfilled with a fixed cam profile.

In this paper, the behavior of a 0.75 L directly air-assisted TC spark-ignited (SI) engine is studied on an aggressive version of the NEDC. The boost, the start and the pump mode are realized with separate cams, while the motor mode is omitted. A cam-shifting architecture is used to change among these modes. The engine considered in this paper is equal to the one used in [6]. Its most important parameters are listed in Table 1. The goal is to find the minimum tank volume. For this purpose, the well-known quasi-static simulation (QSS) [16] technique is applied to a Nissan Micra. The QSS is extended with the tank pressure dynamics, which are

$$p_t(k+1)=p_t\left(k\right)+\frac{R_a·{\vartheta }_t}{V_t}·m_{a,t}({\omega }_e\left(k\right),p_{me}\left(k\right),p_t\left(k\right))$$

(1)

where $R_a$ is the gas constant of air; ${\vartheta }_t$ is the tank temperature; $V_t$ is the tank volume; ${\omega }_e$ is the engine speed; $p_{me}$ is the desired mean effective pressure; and $m_{a,t}$ is the air mass transferred to or from the tank. The variable k indicates the time instant. The terms torque and mean effective pressure are used interchangeably in this paper.

Table 1. Engine data.

Parameter	Symbol	Value	Parameter	Value
engine type		gasoline SI	stroke	66 mm
rated power		61 kW at 6000 rpm	bore	85 mm
rated torque		131 Nm at 3000 rpm	connecting rod	115 mm
displacement	$V_d$	0.75 L	compression ratio	$9.0$
CV diameter	$d_{CV}$	19 mm	no. of cylinders	2, parallel twin

Table 1. Engine data.

Parameter	Symbol	Value	Parameter	Value
engine type		gasoline SI	stroke	66 mm
rated power		61 kW at 6000 rpm	bore	85 mm
rated torque		131 Nm at 3000 rpm	connecting rod	115 mm
displacement	$V_d$	0.75 L	compression ratio	$9.0$
CV diameter	$d_{CV}$	19 mm	no. of cylinders	2, parallel twin

The paper is structured as follows. In Section 2, the air masses transferred in each mode $m_{a,t}$ are investigated. Special attention is paid to the tank pressure dependence. Section 3 discusses the settings of the QSS in order to determine the minimum tank volume. In Section 4, results are presented for the minimum tank size. Furthermore, the sensitivities of the results to the initial tank pressure, the tank size and the gear-shifting strategy are evaluated.

2. Air Mass Transfer of Pneumatic Modes

The air mass transferred in each mode mainly depends on the tank pressure and the engine speed, which both vary during the operation of the engine. In this section a brief summary of the engine modes considered is given. On the one hand, preexisting results are discussed. On the other hand, new results are presented, namely the pressure dependence of the air mass transferred in the boost mode, in the start mode as well as in the pump mode, all with camshaft-driven valves.

2.1. Boost Mode

The boost mode is used primarily to improve the driveability of turbocharged engines by compensating the turbo lag. In [6] it is proposed to size and design the CV according to a desired torque response, i.e., a nominal torque step has to be achieved in a desired time. Furthermore, a lower limit for the tank pressure ${\tilde{p}}_{t,b}$ exists, which should not be underrun to prevent the flow of air–fuel mixture to the tank. Another important finding is that the air mass transferred to the cylinder per valve activation $m_{CV}$ is proportional to the tank pressure and inversely proportional to the engine speed

$$m_{CV}={\mu }_{CV,p}·\frac{p_t}{{\omega }_e}={\mu }_{CV}·\frac{1}{{\omega }_e}$$

(2)

where ${\mu }_{CV,p}$ is a constant that depends on the timing and diameter of the CV. The variable ${\mu }_{CV}$ denotes the CV mass flow. It depends on the tank pressure.

Since the camshaft-driven CV does not allow for a precise dosing of the injected amount of air, the ignition timing is used to control the torque. If there is too much air–fuel mixture in the cylinder, the ignition timing is delayed, which reduces the torque. More details on the torque control can be found in [14].

In [14], the air demand for the entire turbo lag compensation $m_{a,b}$ is presented for various engine speeds and torque requests. The tank pressure was held constant at ${\tilde{p}}_{t,b}$. The resulting nominal air demand ${\tilde{m}}_{a,b}=m_{a,b}\left({\tilde{p}}_{t,b}\right)$ is depicted in the left-hand plot of Figure 2. These results were obtained with a mean value model of the engine system [17]. The CV was sized such that a torque step from partial load to full load can be realized in less than 1 second, which requires a CV mass flow of ${\mu }_{CV,des}=34.9g/s$. In the CV design process appropriate values for ${\mu }_{CV,p}$ and ${\tilde{p}}_{t,b}$ can be found. However, their choice is generally not unique since they are related as follows:

$${\mu }_{CV,des}={\mu }_{CV,p}·{\tilde{p}}_{t,b}$$

(3)

Hence, a desired value of the CV mass flow can be realized by various combinations of ${\mu }_{CV,p}$ and ${\tilde{p}}_{t,b}$. In Equations (4,5) two combinations are listed which are relevant for this paper. Note that for these combinations, the valve timing and diameter are different since the values of ${\mu }_{CV,p}$ differ.

$$\begin{array}{ccc}\hfill {\tilde{p}}_{t,b}=6bar& \to & {\mu }_{CV,p}=5.82g/sbar\hfill \end{array}$$

(4)

$$\begin{array}{ccc}\hfill {\tilde{p}}_{t,b}=10bar& \to & {\mu }_{CV,p}=3.49g/sbar\hfill \end{array}$$

(5)

For the following discussions, the values of Equation (4) are used.

During the operation of the engine, the tank pressure varies. According to Equation (2), the air mass transferred per cycle increases with the tank pressure. The higher CV mass per cycle leads to a faster TC acceleration and thus to a shorter boost time. The right-hand plots in Figure 2 show the resulting air demand for tank pressures higher than ${\tilde{p}}_{t,b}$. The same control strategy is applied as in [14]. The upper plot shows the air mass used as a function of the tank pressure. The lower plot shows the ratio of the air mass used $m_{a,b}$ and the nominal air mass ${\tilde{m}}_{a,b}$ as a function of the ratio of the tank pressure and the lower limit of the tank pressure ${\tilde{p}}_{t,b}$. Several conclusions can be drawn:

• The boost air mass increases with an increasing tank pressure. The influence of the increased boost mass thus is higher than the reduction in the boost time. However, the relative increase in the boost mass is smaller than the relative increase in the tank pressure. The sensitivity, which is defined as

  $$S_p=\frac{m_{a,b}(p_t,{\omega }_e)-{\tilde{m}}_{a,b}\left({\omega }_e\right)}{{\tilde{m}}_{a,b}\left({\omega }_e\right)}·\frac{{\tilde{p}}_{t,b}}{p_t-{\tilde{p}}_{t,b}}$$

  (6)

  is thus smaller than 1;
• At low engine speeds, where the boost mode is used predominantly, the sensitivity $S_p$ is low, e.g., for an increase in tank pressure of 100%, only 20% more air is required at an engine speed of 2000 rpm. The relative increase in the boost mass is larger at high engine speeds. However, the absolute value is rather low;
• The dependence on the desired torque value is low.

Thus, the air mass used for boosting is a function of the engine speed, the desired torque and the tank pressure,

$$m_{a,b}=f({\omega }_e,p_{me},p_t)$$

(7)

Figure 2. (a) Nominal air demand ${\tilde{m}}_{a,b}$ in the boost mode for a turbo lag compensation to various torques at various engine speeds with $p_t={\tilde{p}}_{t,b}$; and (b) air demand $m_{a,b}$ for various tank pressures: Dashed: $p_{me}=13\mathrm{bar}$. Thin solid: $p_{me}=15\mathrm{bar}$. Thick solid: $p_{me}=17\mathrm{bar}$. CV size used ${\mu }_{CV,p}=5.82\mathrm{g}/\mathrm{sbar}$.

Figure 2. (a) Nominal air demand ${\tilde{m}}_{a,b}$ in the boost mode for a turbo lag compensation to various torques at various engine speeds with $p_t={\tilde{p}}_{t,b}$; and (b) air demand $m_{a,b}$ for various tank pressures: Dashed: $p_{me}=13\mathrm{bar}$. Thin solid: $p_{me}=15\mathrm{bar}$. Thick solid: $p_{me}=17\mathrm{bar}$. CV size used ${\mu }_{CV,p}=5.82\mathrm{g}/\mathrm{sbar}$.

2.2. Pneumatic Start Mode

Engines starting faster than 350 ms can be realized with the pneumatic start mode. Hence, this mode can be used as a stop/start system and to eliminate the idling consumption. As shown in [13], the cam profile of the start mode is also sized according to a performance criterion, such as to reach an engine speed of 1200 rpm in 350 ms. There is also a lower limit for the tank pressure ${\tilde{p}}_{t,s}$, which should not be underrun in order to fulfill the desired start performance.

In this section, the start performance is analyzed with respect to the air demand $m_{a,s}$ and the start duration $t_s$ for various tank pressures $p_t\ge {\tilde{p}}_{t,s}$. The optimal CV design presented in [13] is used, i.e., ${\tilde{p}}_{t,s}=10\mathrm{bar}$. Figure 3 shows the results for various tank pressures. The first plot shows the total amount of air used $m_{a,s}$ and the number of power strokes $N_{ps}$ required to reach the desired engine speed. The second plot shows the time duration $t_s$ until the desired engine speed is reached. These results were obtained with the process model described in [13].

The amount of air used to start the engine is calculated as the integral of the air mass flow through the CV. The same air consumption is thus required if a large mass flow is present for a short time or if a small mass flow occurs for a longer time duration. For instance, the air consumptions for $p_t=9.3\mathrm{bar}$ and $p_t=12\mathrm{bar}$ are equal. However, the start times are different.

A higher tank pressure leads to a higher air mass flow. The torque exerted is larger, which leads to a shorter start time $t_s$. The total amount of air used for an engine start $m_{a,s}$ is a piecewise continuous function of the tank pressure. The steps occur when the number of power strokes $N_{ps}$ changes. For an equal number of power strokes the amount of air required increases as the tank pressure increases mainly because the valve cannot be closed when the desired engine speed is reached.

Figure 3. Air consumption $m_{a,s}$, number of power strokes $N_{ps}$ and start time $t_s$ of the pneumatic start at various tank pressures.

Figure 3. Air consumption $m_{a,s}$, number of power strokes $N_{ps}$ and start time $t_s$ of the pneumatic start at various tank pressures.

The start time is also a piecewise continuous function of the tank pressure. However, it strictly decreases as the tank pressure increases. For tank pressures lower than 10 bar, the start lasts longer than 350 ms and thus does not fulfill the performance goal. However, a start is still possible.

The air demand of the pneumatic start is thus a function of the tank pressure,

$$m_{a,s}=f\left(p_t\right)$$

(8)

2.3. Pneumatic Pump Mode

To enable the boost mode and pneumatic engine starts, compressed air has to be available. To avoid a negative impact on the fuel consumption, the energy required for the air compression should not stem from the combustion. During the vehicle deceleration, the braking energy can be used to compress air. In the pump mode, the engine is operated as an air compressor. Since the valve timing cannot be altered, the torque absorbed by the engine cannot be controlled. It is thus a function of the tank pressure, the engine speed, and the CV design chosen.

In this section, the pump mode characteristics are discussed first. Special attention is paid to the engine speed and the tank pressure dependencies. Then, the influence of the CV timing is analyzed. Finally, a design approach is presented.

2.3.1. Characteristics

To study the characteristics of the pump mode realized with a fixed cam profile, a process model of the engine is used. Figure 4 shows the air mass transferred per cycle ${\overline{m}}_{a,p}$ and the average mass flow from the cylinder to the tank ${\dot{m}}_{a,p}$ for a fixed CV timing. The average mass flow ${\dot{m}}_{a,p}$ is calculated as follows:

$${\dot{m}}_{a,p}={\overline{m}}_{a,p}·\frac{{\omega }_e}{4·\pi }$$

(9)

Figure 4. Pump mode performance. (a) Air mass transferred per cycle from cylinder to tank; and (b) mean air mass flow from cylinder to tank.

Figure 4. Pump mode performance. (a) Air mass transferred per cycle from cylinder to tank; and (b) mean air mass flow from cylinder to tank.

The main effects which determine the air mass transferred per cycle for a constant tank pressure are the duration of the CV being open and the cylinder filling at intake valve closing. For low engine speeds, the duration is rather long. However, the cylinder filling is rather poor due to late intake valve closing of the engine considered ($66{}^{\circ }$ crank angle after bottom dead center). As the engine speed increases, the better filling performance first leads to an increased mass transfer to the tank. Eventually, the reduced opening duration becomes the dominant effect, and the air mass transferred is reduced. The value of ${\overline{m}}_{a,p}$ decreases with an increasing tank pressure since it takes longer until the cylinder pressure reaches the tank pressure level. Hence, the time duration with a high enough cylinder pressure is shorter. Consequently, at a low tank pressure and a low engine speed, the air mass transferred per cycle is maximal because of the long duration with a large pressure difference.

However, the mean air mass flow to the tank is maximal at a low tank pressure and a high engine speed. The lower air mass per cycle is overcompensated by the higher number of air transfers per time.

These relations generally hold. The tank-filling performance is best at low tank pressures and high engine speeds. Thus, it is always advantageous to operate the pump mode at a high engine speed. The gear selection during the deceleration where the pump mode is operated could potentially be used to improve the tank-filling performance. Thus, if a vehicle is equipped with an automatic or semi-automatic gear box, these characteristics should be included in the gear box control to promote operating points with a high filling performance, e.g., early downshift during deceleration.

Therefore, the air transfer in the pump mode is a function of the engine speed and the tank pressure,

$${\dot{m}}_{a,p}=f({\omega }_e,p_t)$$

(10)

2.3.2. Influence of the Valve Opening

Apart from the engine speed and the tank pressure, the pump performance depends on the valve timing. Figure 5 shows the performance for a CV that opens later than the one shown in Figure 4. The performance is better at high tank pressures and worse at higher engine speeds. This design is advantageous if the tank pressure level during the engine operation is rather high.

Figure 5. Pump mode performance for a later CV opening than in Figure 4. (a) Air mass transferred per cycle from cylinder to tank; and (b) mean air mass flow from cylinder to tank.

Figure 5. Pump mode performance for a later CV opening than in Figure 4. (a) Air mass transferred per cycle from cylinder to tank; and (b) mean air mass flow from cylinder to tank.

2.3.3. Cam Design Methodology

As seen in the previous section, the valve timing substantially influences the pump performance. The operating conditions, i.e., tank pressure and engine speed, vary substantially during the engine operation. As opposed to a variable CV, the timings of the camshaft driven CV cannot be altered during the operation. The challenge is to find good values for the CV timing which perform well under various operating conditions. In this section a method for the derivation of the CV timing is proposed.

The goal of the method is to find values for the CV timing, i.e., the opening instant of the CV ${\varphi }_{CVO,p}$ and the closing instant ${\varphi }_{CVC,p}$ of the CV, respectively. The CV acceleration is assumed to be as high as possible.

In order to determine the CV timing the air transfer is evaluated at several operating points. Each operating point is characterized by a tank pressure and an engine speed. The optimal CV timings maximize the weighted sum of the air masses transferred in n operating points ${\Omega }_i=\{{\omega }_{e,i},p_{t,i}\}\in \Omega ={\mathbb{R}}^{n\times 2,+}$, that is

$$\{{\varphi }_{CVO,p}^{*},{\varphi }_{CVC,p}^{*}\}=\text{argmax}\sum _{i=1}^n{w}_i·{\dot{m}}_{a,p}({\Omega }_i,{\varphi }_{CVO,p},{\varphi }_{CVC,p})$$

(11)

where $w_i\ge 0$ is the weighting factor of the operating point i. It can be used to penalize specific operating points or operating regions. The weighting factor can be chosen as a function of the tank pressure and/or of the engine speed since they both vary during the operation. It is reasonable to penalize tank pressures more strongly that are close to the lower limits of the boost and the start mode because there a good filling performance is desirable. The optimization problem can be solved with a numerical optimization method.

The n operating points in Ω should be selected reasonably, i.e., by considering the requirements of the boost and the start modes, such as lower limits of the tank pressure, and by considering the operating points which most frequently occur on a drive cycle.

3. System Design Method

Now that the characteristics of all pneumatic engine modes are known, the tank size can be determined. For the derivation of the minimum tank size a QSS is performed to find the tank pressure trajectory on a drive cycle. As shown in Equation (1) the tank pressure results from the various masses transferred to and from the tank. The tank is assumed to be iso-thermal.

The mode selection is crucial for the determination of the tank pressure trajectory. In [11] the mode selection of the HPE was effected based on the solution of an optimal control problem. The optimization was necessary because for certain driving conditions the torque could have been provided by either the combustion mode or the pneumatic motor mode. Since the pneumatic motor mode is omitted in the air-assisted TC SI engines, this degree of freedom is no longer available. Thus, an optimization is no longer necessary.

For the engine considered, the activation criteria of the pump and the start mode are trivial, i.e., to pump when the kinetic energy loss is larger than the work necessary to compress air and to start the engine after it was stopped, respectively. The boost mode activation criterion is more challenging. It is discussed in this section.

Given that all criteria are known, the tank pressure trajectory can be calculated for a given tank volume $V_t$. The minimum tank pressure of the resulting tank pressure trajectory should be larger than or equal to the lower limit of the tank pressure ${\tilde{p}}_t$. Furthermore, a charge-sustaining solution is desirable, i.e., the tank pressure at the end of the drive cycle is larger than or equal to the initial tank pressure, which is equal to $p_t\left(0\right)=12\mathrm{bar}$. The minimum tank volume ${\tilde{V}}_t$ is the smallest tank volume which fulfills both conditions. It can be found by a nonlinear optimization method. Alternatively, the feasibility of a given tank size can be evaluated.

3.1. Boost Mode Activation

As opposed to a naturally aspirated engine, due to the turbo lag, a TC SI engine cannot perform every change in operating point within the typical sample time of a QSS $T_s=1\mathrm{s}$.

One option to formulate the activation criterion is a list of conditions which have to be fulfilled, e.g.

$$\begin{array}{cc}\hfill p_{me}\left(k\right)-p_{me}(k-n)& >\Delta p_{me,thr}(.)\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill p_{me}\left(k\right)& >p_{me,thr}(.)\hfill \end{array}$$

(13)

where $k\ge n\ge 1$. In this formulation, the boost mode is activated if the torque change is larger than a threshold value $\Delta p_{me,thr}(.)$ and the desired torque is larger than a threshold value $p_{me,thr}(.)$ (which is typically in the turbocharged region). The list of conditions can be extended arbitrarily with conditions on the engine speed, the turbocharger speed, etc. Furthermore, the threshold values can either be constants or functions, e.g., of the engine speed.

Instead of the mean effective pressure, the accelerator signal $u_{th}$ can be used to determine the activation of the boost mode. The accelerator signal is better suited because it contains information about the driver’s intention. Analogously, the activation criterion can be formulated as a list of conditions on the accelerator signal.

Alternatively, by means of a dynamic engine model, a formulation of the turbo lag suitable for QSS can be derived. The boost mode is thus activated if the operating point requested at time step k cannot be reached without boosting,

$$p_{me}\left(k\right)\ge p_{me,max}({\omega }_e\left(k\right),p_{me}(k-1),{\omega }_e(k-1))$$

(14)

where $p_{me,max}$ denotes the highest torque that can be reached in the sample time $T_s$ without boosting.

For the derivations in this paper, the list of conditions on the mean effective pressure is used with the following parameterization: $\Delta p_{me,thr}=5\mathrm{bar}$, $p_{me,thr}=12\mathrm{bar}$, and $n=1$.

For the evaluation of the air demand in the boost mode [see Equation (7)] the maximum torque value of the upcoming 3 s is used

$$p_{me,b}\left(k\right)=\underset{i\in [k,k+3s/T_s]}{max}{p}_{me}\left(i\right)$$

(15)

3.2. Drive Cycle

Apart from the activation criterion, the drive cycle considered influences the tank size, e.g., the number of starts or the number of boosts. Drive cycles developed for the determination of the fuel consumption generally are not suitable for the tank sizing. The velocity trajectories of most of them, e.g., NEDC, Worldwide Harmonized Light Duty Test Procedure, Federal Test Procedure (FTP), are too gradual to require boosting. For the tank size evaluation, a designated drive cycle needs be used, e.g., a drive cycle that captures the most aggressive driving that may be desired with the vehicle considered. For a worst case analysis, the drive cycle should contain many boosts at low engine speeds and many engine starts.

The drive cycle chosen in this paper is an aggressive version of the NEDC, called the aNEDC. The vehicle acceleration on the aNEDC is three times higher than in the regular NEDC. The gears are selected in accordance with the regular version, i.e., shifting occurs at the same vehicle speed. Figure 6 shows the speed and gear profiles of both drive cycles.

Figure 6. Comparison of velocity $v_v$ and gear trajectories of the NEDC and the aNEDC on the last part of the ECE and on the EUDC.

Figure 6. Comparison of velocity $v_v$ and gear trajectories of the NEDC and the aNEDC on the last part of the ECE and on the EUDC.

3.3. Vehicle and Engine Data

In this paper, a Nissan Micra is considered in the QSS. The corresponding vehicle data is listed in Table 2. The longitudinal vehicle dynamics used to determine the engine speed and the mean effective pressure are described in the appendix.

As mentioned in the introduction of this paper, a 0.75 L TC SI engine is used. It replaces the standard 1.24 L naturally aspirated engine. Both engines have approximately the same rated power. In [11], a fuel-saving potential of $28\%$ was validated by experiments on the FTP for this replacement. The pneumatic motor mode was not used.

Table 2. Vehicle data: Nissan Micra.

Parameter	Symbol	Value	Parameter	Symbol	Value
vehicle base mass	$m_v$	$1150\mathrm{kg}$	final gear ratio	${\gamma }_{fg}$	$4.07$
wheel radius	$r_w$	$0.2851\mathrm{m}$	1st gear ratio	$\gamma \left(1\right)$	$3.73$
rolling friction coeff.	$c_{r,0}$	$0.0076$	2nd gear ratio	$\gamma \left(2\right)$	$2.15$
rolling friction coeff.	$c_{r,1}$	$5.1·{10}^{-6}\mathrm{s}/\mathrm{m}$	3rd gear ratio	$\gamma \left(3\right)$	$1.39$
air resistance	$A_f·c_d$	$0.8575{\mathrm{m}}^2$	4th gear ratio	$\gamma \left(4\right)$	$1.03$
			5th gear ratio	$\gamma \left(5\right)$	$0.82$

Table 2. Vehicle data: Nissan Micra.

Parameter	Symbol	Value	Parameter	Symbol	Value
vehicle base mass	$m_v$	$1150\mathrm{kg}$	final gear ratio	${\gamma }_{fg}$	$4.07$
wheel radius	$r_w$	$0.2851\mathrm{m}$	1st gear ratio	$\gamma \left(1\right)$	$3.73$
rolling friction coeff.	$c_{r,0}$	$0.0076$	2nd gear ratio	$\gamma \left(2\right)$	$2.15$
rolling friction coeff.	$c_{r,1}$	$5.1·{10}^{-6}\mathrm{s}/\mathrm{m}$	3rd gear ratio	$\gamma \left(3\right)$	$1.39$
air resistance	$A_f·c_d$	$0.8575{\mathrm{m}}^2$	4th gear ratio	$\gamma \left(4\right)$	$1.03$
			5th gear ratio	$\gamma \left(5\right)$	$0.82$

3.4. Mode Specifications

In the previous section, control-oriented models of the engine modes were presented. Both the boost and the start mode were shown to require a lower limit of the tank pressure. The lower limit of the system is equal to

$${\tilde{p}}_t=max({\tilde{p}}_{t,b},{\tilde{p}}_{t,s})={\tilde{p}}_{t,s}=10\mathrm{bar}$$

(16)

Hence, for the boost mode, the design values given in Equation (5) are used. For the start mode, the values of the air mass demand shown in Figure 3 is used.

The valve timings of the pump mode are found by solving Equation (11) for the operating point $\Omega =\{2000\mathrm{rpm},10\mathrm{bar}\}$. This engine speed occurs most frequently during the deceleration phases on the aNEDC. The air transfer map resulting from the optimal valve timing is equal to the one shown in Figure 5. The air mass transferred per time step in a QSS is equal to $m_{a,p}={\dot{m}}_{a,p}·T_s$, where $T_s$ is the sample time.

4. Simulation Results and Discussion

The minimum air tank volume is found to be ${\tilde{V}}_t=9.25L$. Figure 7 shows the resulting trajectories of the torque, the engine speed and the tank pressure. It can be seen that boosting generally is necessary when shifting up or during accelerations in high gears. The tank volume is limited by the lower limit of the tank pressure. At the beginning of the drive cycle, two starts and one boost demand air. However, the recuperation potential of the first deceleration is limited. Therefore, at $t=127\mathrm{s}$ the tank pressure is equal to the lower limit.

Figure 7. Mean effective pressure $p_{me}$, engine speed ${\omega }_e$ and tank pressure $p_t$ trajectories on the aNEDC drive cycle. The black dots indicate boosts.

Figure 7. Mean effective pressure $p_{me}$, engine speed ${\omega }_e$ and tank pressure $p_t$ trajectories on the aNEDC drive cycle. The black dots indicate boosts.

At the end of the drive cycle, the tank pressure is higher by 2.4 bar than at the beginning. Hence, the solution is charge sustaining. The net increase in air-stored $\Delta M_{a,t}$ amounts to 25 g. The specifications on the pneumatic start mode thus represent a lower boundary on the tank volume because of the high value of ${\tilde{p}}_t$.

Table 3 lists the values of the cumulative air masses transferred in each mode $M_{a,l}$ with $l=\{b,s,p\}$. The drive cycle chosen requires 18 boosts and has 13 engine starts. More air is used for starting than for boosting. In the pump mode 253 g of air is charged during $t_p=135\mathrm{s}$.

Table 3. Cumulative air masses transferred in each mode on the aNEDC for the minimum tank size.

$M_{a,b}$	$M_{a,s}$	$M_{a,p}$	$\Delta M_{a,t}$	# boosts	# starts	$t_p$
101 g	127 g	253 g	25 g	18	13	135 s

Table 3. Cumulative air masses transferred in each mode on the aNEDC for the minimum tank size.

$M_{a,b}$	$M_{a,s}$	$M_{a,p}$	$\Delta M_{a,t}$	# boosts	# starts	$t_p$
101 g	127 g	253 g	25 g	18	13	135 s

4.1. Dependence on the Initial Tank Pressure

If the initial tank pressure is close to the lower limit of the tank pressure, a large tank volume is necessary to avoid a pressure drop below ${\tilde{p}}_t$ during the first engine start. At a large initial tank pressure the tank volume can be much smaller. Figure 8 shows the relation between the initial tank pressure and the minimum tank size. Thus, an initial tank pressure should be selected which is in the middle between the minimum (= 10 bar) and the maximum (= 15.5 bar) tank pressures.

Figure 8. Minimum tank volume ${\tilde{V}}_t$ as a function of the initial tank pressure $p_t\left(0\right)$.

Figure 8. Minimum tank volume ${\tilde{V}}_t$ as a function of the initial tank pressure $p_t\left(0\right)$.

4.2. Influence of the Tank Size

Besides the air mass transferred to and from the tank, the tank pressure trajectory is influenced by the tank size [see Equation (1)]. In this section, the results of a small and a large tank are compared. For that purpose, a QSS is performed for $V_t={\tilde{V}}_t=9.25\mathrm{L}$ and $V_t=18.5\mathrm{L}$. Figure 9 shows the resulting tank pressure trajectories. It is noticeable that the amplitude of the pressure oscillations is smaller for a large tank volume. This observation is in line with the relation given in Equation (1) which suggests that the addition or the removal of a defined amount of air leads to a smaller change in the tank pressure if the tank volume is large.

Figure 9. Tank pressure trajectories for two different tank volumes.

Figure 9. Tank pressure trajectories for two different tank volumes.

Table 4 lists the total amount of air transferred in each mode. Boosting requires the same amount of air with both tank sizes due to its low dependence on the tank pressure. With the larger tank, starting requires slightly less air since the tank pressure at the engine start is lower. However, in the pump mode 3% more air is transferred to the larger tank. On the one hand, this increase is due to the longer duration with pumping (+8 s). On the other hand, it is a result of the better filling performance which is due to the lower tank pressure level. For a small tank, due to the lower tank pressure, the filling performance at the beginning of a deceleration phase is usually better than the one with a large tank. However, as a result of the small tank, the tank pressure increases faster, which leads to a decrease of the filling efficiency below the one achieved with a large tank. Furthermore, the instant at which no more air can be transferred is reached earlier with a smaller tank. Thus, the filling duration with a small tank tends to be shorter.

Table 4. Cumulative air masses transferred in each mode on the aNEDC for two different tank sizes.

Tank volume	$M_{a,b}$	$M_{a,s}$	$M_{a,p}$	$\Delta M_{a,t}$	$t_p$
$V_t=9.25\mathrm{L}$	101 g	127 g	253 g	25 g	135 s
$V_t=18.5\mathrm{L}$	101 g	125 g	261 g	35 g	143 s
	$+0.0\%$	$-1.6\%$	$+3.2\%$	$+40.0\%$	$+5.9\%$

Table 4. Cumulative air masses transferred in each mode on the aNEDC for two different tank sizes.

Tank volume	$M_{a,b}$	$M_{a,s}$	$M_{a,p}$	$\Delta M_{a,t}$	$t_p$
$V_t=9.25\mathrm{L}$	101 g	127 g	253 g	25 g	135 s
$V_t=18.5\mathrm{L}$	101 g	125 g	261 g	35 g	143 s
	$+0.0\%$	$-1.6\%$	$+3.2\%$	$+40.0\%$	$+5.9\%$

Finally, the increase of the air mass $\Delta M_{a,t}$ over the complete cycle for the large tank is $40\%$ higher than for the small tank. Besides the increased air mass at the end of the drive cycle, the safety margin, i.e., the distance of the tank pressure trajectory to ${\tilde{p}}_t$, is considerably larger with a larger tank. Hence, the system design is more robust to errors in the assumptions and to disturbances.

4.3. Influence of the Gear-Shifting Strategy

Aside from its dependence on the tank pressure, the filling performance is also influenced by the engine speed. In general, the performance is better at high engine speeds. Therefore, the system behavior is analyzed for an alternative gear profile. In this profile, during the deceleration phases, the gear is one smaller than in the standard profile, which leads to higher engine speeds. Figure 10 shows the gear and engine speed trajectories of the two gear profiles.

Figure 10. Gear number and engine speed ${\omega }_e$ for the gear profiles considered on representative sections of the aNEDC.

Figure 10. Gear number and engine speed ${\omega }_e$ for the gear profiles considered on representative sections of the aNEDC.

The left-hand plot of Figure 11 shows the resulting tank pressure trajectories. The right-hand plot shows the air masses consumed during the various engine starts. Table 5 lists the values of the air masses transferred. As a result of the downshift, the average engine speed in the pump mode ${\overline{\omega }}_{e,p}$ is substantially higher with the alternative profile. More air is thus transferred per time step, but the total amount of air transferred is smaller because the pump time is lower. The reduction of the pump time is due to the fact that the torque available after downshifting is often too small to enable the pump mode.

Figure 11. (a) Tank pressure trajectories for the gear profiles considered on the entire drive cycle and (b) air mass consumption of the various engine starts. $V_t=9.25\mathrm{L}$.

Figure 11. (a) Tank pressure trajectories for the gear profiles considered on the entire drive cycle and (b) air mass consumption of the various engine starts. $V_t=9.25\mathrm{L}$.

Table 5. Cumulative air masses transferred in each mode on the aNEDC for various gear profiles.

Gear profile	$M_{a,b}$	$M_{a,s}$	$M_{a,p}$	$\Delta M_{a,t}$	$t_p$	${\overline{\omega }}_{e,p}$
standard	101 g	127 g	253 g	25 g	135 s	2000 rpm
alternative	102 g	107 g	239 g	30 g	117 s	2700 rpm
	$+1\%$	$-16\%$	$-6\%$	$+20\%$	$-13\%$

Table 5. Cumulative air masses transferred in each mode on the aNEDC for various gear profiles.

Gear profile	$M_{a,b}$	$M_{a,s}$	$M_{a,p}$	$\Delta M_{a,t}$	$t_p$	${\overline{\omega }}_{e,p}$
standard	101 g	127 g	253 g	25 g	135 s	2000 rpm
alternative	102 g	107 g	239 g	30 g	117 s	2700 rpm
	$+1\%$	$-16\%$	$-6\%$	$+20\%$	$-13\%$

Furthermore, the air demand for the engine starts is substantially smaller. The tank pressure is often high enough to allow for an engine start with only two power strokes. The right-hand plot in Figure 11 shows the air consumption of the various engine starts. Clearly, the air consumption with the alternative profile is generally lower.

The amount of air used for boosting is barely influenced, which is due to the low dependence of the air mass used on the tank pressure as mentioned in Section 2.1.

In conclusion, downshifting during the deceleration phase is advantageous since the tank pressure level is increased and more air is stored at the end of the drive cycle. However, the higher engine speeds have an impact on the driving comfort.

5. Conclusions

By using a camshaft-driven charge valve, the additional system costs and complexity are reduced in comparison to an HPE with fully variable valves. In-cylinder boosting, as well as pneumatic engine starts, can still be realized while the pneumatic motor mode is omitted. In the boost mode, the air demand increases with the tank pressure. However, the ratio of the relative increase in air and the relative increase of the tank pressure is smaller than 1. Particularly for low engine speeds, where boosting is primarily applied, the sensitivity to the tank pressure is low. The start mode shows a piecewise continuous dependence on the tank pressure. The discontinuity results from the number of power strokes required to reach the desired engine speed. For each piecewise section, the air demand increases with the tank pressure. The pump performance is strongly influenced by the opening instant of the charge valve. An early opening is favorable if the tank pressure level is low. A late opening is preferred if the lower limit on the tank pressure is high.

By means of a quasi-static simulation, which was extended by the tank pressure dynamics, the minimum tank volume was determined for a compact class vehicle. A tank volume of less than 10 L was found to be sufficient. The tank volume is mainly influenced by the performance specifications of the pneumatic start. If a slower start were acceptable, the tank size could be reduced.

Additional investigations have shown that the system is strongly coupled. Downshifting during the deceleration phases was found to increase the tank pressure level. Furthermore, the amount of air stored in the tank at the end of the drive cycle can be increased. However, the determination of the optimal gear profile is not straightforward. The nonlinear dependence of the start air demand on the tank pressure poses a major challenge. As a next step, the optimal gear profile should be determined with a model-based optimization.