Assessing Tolerance-Based Robust Short-Term Load Forecasting in Buildings
Abstract
:1. Introduction
- Weatherproofing, insulation and automatic HVAC (heating, ventilation, and air conditioning).
- Energy re-utilisation (as in co- or tri-generation).
- Use of renewable energy sources and energy storage systems.
- Demand response controllers attached to the HVAC and other loads.
- New Pattern: Some days show a different consumption pattern due to reasons of diverse nature (e.g., long weekends, sport events, election polls, strikes, etc.). In the end, the load of these days consists of a new day-type on its own (see Section 3 for more details) and it should be removed from the learning set or classified beforehand.
- Scaled Pattern: On the other hand, some days follow profiles similar to those from existing day-types but scaled down or up. Again, these changes can be due to diverse causes (e.g., sudden weather changes, long weekends, special events, works, etc.). The load in these days does not consist of a new day-type but can be just an extreme statistical fluctuation or simply represent an underline change in the building (such as new equipment) that may be extended along the time. In the first case, there should be no action, but in the second one, the learning window should be restarted.
2. Related Work
3. Adaptive STLF in Buildings
3.1. Overall Methodology

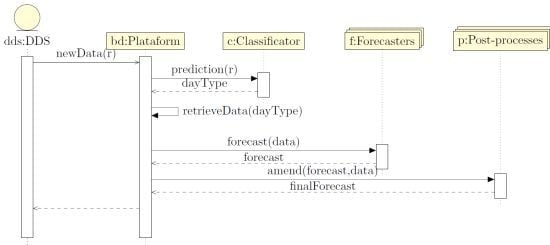
- Data Distribution Service (DDS): A meter sends a new measure to the Platform through the DDS bus. This measure is stored to then be used to issue a forecast.
- Classificator: In this step, the Platform sends the new data to the Classificator and queries it for the prediction of the day-type for the next day. In previous works [30], we have compared several clustering techniques with the use of the local work calendar. Our results conclude that the best option is to use the work calendar if it is available. Hence, buildings may present different number of day-types. Specifically, in our tests, there are buildings presenting:
- -
- -
- -
- Four day-types: (Weekday, Saturdays, Sundays and Bank Holidays) such as . This building shows a special behaviour in Bank Holidays. In Figure 5 can be seen an example of this behaviour.
- Forecasters: In the next step, the Platform sends the data of the previous days of the same day-type to the Forecasters. They will adjust the model parameters and then issue a forecast. Note that we have a different model for every day-type, and therefore we must re-train the model for every day.

- Post-processes: Finally, in this stage the Platform sends the forecasts issued by the forecasters to the post-processes in order to improve the results. Examples post-process are:
- -
- Bias Correction: some models produce forecast that are systematically biased. We can measure that bias and compensate it. In [10] we have assessed the performance of this post-process.
- -
- Model Selection: some models issue a more reliable forecast at certain hours or day-types than others. In [13], we presented a comparison of different strategies to select the best model in every moment.
- -



3.2. Proposed Post-Process Methods
- Learning Window Re-Initialization: In this case, we reboot the learning windows in order to avoid anomalies of the scaled pattern type (i.e., we completely delete the data in the dataset and replace it with the newest value). Since the learning windows are very short (just three days in this test, see [10,13] for a broad comparison in this matter) and the models used are sufficiently robust to tailor this degenerated training set, we are able to issue a new forecast in this situation. Moreover, the forecast produced is the obvious one, just the values observed the previous day (i.e., acts like a Random Walk Model), so this adjustment quickly adapts to changes in the dataset.
- Skipping Anomalies: In this case we avoid introducing the new pattern in the training data in order to avoid anomalies of the new pattern type.
3.3. Forecasting Models
3.3.1. Time Series Model
3.3.2. Support Vector Machines Model
4. Datasets
| Building | HVAC | Number of day-types | Expected MAPE (%) |
|---|---|---|---|
| NO | 3 | 6.01 | |
| NO | 3 | 8.22 | |
| YES | 3 | 13.60 | |
| YES | 3 | 8.74 | |
| NO | 3 | 5.89 | |
| YES | 4 | 7.22 | |
| Partially | 3 | 4.82 | |
| NO | 3 | 5.95 | |
| N/A | 2 | 4.98 | |
| N/A | 2 | 3.74 |
| Region | Expected MAPE (%) | MAPE from Operator (%) |
|---|---|---|
| 5.87 | 1.08 | |
| 9.20 | N/A | |
| 7.45 | 5.02 | |
| 6.95 | 1.64 | |
| 2.04 | 3.57 |
4.1. Buildings
4.1.1. University of Deusto
4.1.2. Ashrae competition
4.1.3. Casaccia Research Centre
4.2. Regions
- : the Spanish TSO [37], from January 2007 until October 2011.
- : the Pennsylvania, Jersey, and Maryland Interconnection (PJM) [38], more accurately from the Allegheny Power (AP) zone, from November 2008 until December 2010.
- and : the New York Independent System Operator (NYISO) [39], more accurately from the NYC and NORTH substations. The former contains data from February 2005 until October 2011, the latter from June 2001 to October 2011.
- : from the Eastern Slovakian TSO (Eunite competition dataset [40]), from January 1997 to December 1998.

4.3. Test-Bed and Validation Measurements
5. Experimental Results

| Datasets | 5 | 10 | 15 | 20 | 25 | 30 | 40 | |
|---|---|---|---|---|---|---|---|---|
| 6.42 | 6.08 | 6.05 | 6.03 | 6.05 | 6.1 | 0 | 6.1 | |
| 13.1 | 12.79 | 12.52 | 12.61 | 12.51 | 12.34 | 12.35 | 12.48 | |
| 13.1 | 12.65 | 12.19 | 12.1 | 12.16 | 11.97 | 11.95 | 12.33 | |
| 13.31 | 13.02 | 12.85 | 12.91 | 12.89 | 13.02 | 12.88 | 12.86 | |
| 10.59 | 10.23 | 9.86 | 9.77 | 9.85 | 9.95 | 9.95 | 9.95 | |
| 11.68 | 11.53 | 11.48 | 11.57 | 11.51 | 11.7 | 11.96 | 12.04 | |
| 11.91 | 11.41 | 11.18 | 11.14 | 11.47 | 11.07 | 11.07 | 11.07 | |
| 11.5 | 11.18 | 10.79 | 10.49 | 10.49 | 10.49 | 0 | 10.64 | |
| 12.11 | 11.97 | 11.69 | 11.14 | 11.1 | 11.1 | 11.1 | 11.24 | |
| 4.8 | 4.63 | 4.63 | 4.65 | 4.65 | 4.65 | 0 | 4.66 | |
| 7.23 | 7.26 | 7.25 | 7.23 | 7.21 | 7.2 | 7.19 | 7.19 | |
| 6.21 | 6.34 | 6.38 | 6.39 | 6.39 | 6.39 | 0 | 6.37 | |
| 2.82 | 2.8 | 2.8 | 2.8 | 2.8 | 2.8 | 2.8 | 2.77 | |
| 3.71 | 3.63 | 3.63 | 3.62 | 3.62 | 0 | 0 | 3.62 | |
| 5.54 | 5.86 | 5.94 | 5.93 | 5.93 | 5.93 | 0 | 5.93 |
| Datasets | 5 | 10 | 15 | 20 | 25 | 30 | 40 | |
|---|---|---|---|---|---|---|---|---|
| 7.14 | 6.68 | 6.64 | 6.64 | 6.72 | 6.82 | 0 | 6.38 | |
| 13.68 | 13.56 | 13.34 | 13.44 | 13.31 | 13.05 | 13.09 | 12.99 | |
| 13.19 | 12.37 | 12.41 | 12.65 | 13.26 | 12.36 | 12.36 | 12.74 | |
| 13.33 | 13.29 | 13.23 | 13.48 | 13.8 | 14.06 | 13.59 | 13.72 | |
| 10.97 | 10.82 | 10.73 | 10.37 | 10.8 | 10.85 | 10.85 | 10.62 | |
| 13.84 | 13.42 | 13.61 | 13.51 | 13.78 | 14.67 | 14.73 | 13.29 | |
| 12 | 11.47 | 11.22 | 10.91 | 11.66 | 10.88 | 10.78 | 10.45 | |
| 11.87 | 11.52 | 11.06 | 10.89 | 10.84 | 11.24 | 0 | 11.24 | |
| 11.91 | 11.84 | 11.88 | 11.3 | 11.26 | 11.26 | 0 | 11.74 | |
| 5 | 4.62 | 4.64 | 4.73 | 4.73 | 4.73 | 0 | 4.8 | |
| 7.49 | 7.95 | 7.88 | 7.91 | 7.87 | 7.81 | 7.8 | 7.78 | |
| 6.14 | 6.22 | 6.3 | 6.32 | 6.32 | 6.33 | 6.33 | 6.31 | |
| 2.92 | 2.91 | 2.91 | 2.91 | 2.92 | 2.92 | 2.92 | 2.88 | |
| 3.88 | 3.84 | 3.83 | 3.83 | 3.84 | 0 | 0 | 3.79 | |
| 5.73 | 6.69 | 6.75 | 6.74 | 6.74 | 6.74 | 0 | 6.75 |
| Datasets | AR | SVM | ||||
|---|---|---|---|---|---|---|
| k | Post-process | Normal | k | Post-process | Normal | |
| 20 | 5.74 | 9.04 | – | – | – | |
| 30 | 24.53 | 25.91 | – | – | – | |
| 40 | 12.81 | 22.86 | 30 | 18.87 | 27.68 | |
| – | – | – | 15 | 15.69 | 16.59 | |
| 20 | 5.54 | 7.92 | 20 | 8.06 | 12.7 | |
| 15 | 10.96 | 12.52 | – | – | – | |
| 20 | 9.7 | 11.29 | 25 | 10.52 | 17.83 | |
| 25 | 8.01 | 11 | 25 | 7.97 | 18.04 | |
| 10 | 8.83 | 9.08 | 10 | 7.93 | 9.51 | |
| 5 | 6.68 | 7.07 | 5 | 7.1 | 7.59 | |
| 5 | 6.18 | 6.71 | 5 | 6.28 | 7.76 | |
6. Conclusions
Acknowledgements
- ENERGOS CEN2009-1048 project (funded by Spanish CENIT R&D Programme);
- ITEA2 NEMO&CODED IDI-20110864 and IMPONET TSI-020400-2010-0103 projects (funded by Spanish Industry, Tourism and Commerce Ministry).
References
- Feinberg, E.; Genethliou, D. Load Forecasting. In Applied Mathematics for Restructured Electric Power Systems: Optimization, Control, and Computational Intelligence; Springer: Berlin, Germany, 2005; pp. 269–285. [Google Scholar]
- Hinojosa, V.; Hoese, A. Short-term load forecasting using fuzzy inductive reasoning and evolutionary algorithms. IEEE Trans. Power Syst. 2010, 25, 565–574. [Google Scholar] [CrossRef]
- Kyriakides, E.; Polycarpou, M. Short term electric load forecasting: A tutorial. Stud. Comput. Intell. 2009, 35, 391–418. [Google Scholar]
- Alfares, H.; Nazeeruddin, M. Electric load forecasting: Literature survey and classification of methods. Int. J. Syst. Sci. 2002, 33, 23–34. [Google Scholar] [CrossRef]
- Yang, H.; Huang, C. A new short-term load forecasting approach using self-organizing fuzzy ARMAX models. IEEE Trans. Power Syst. 1998, 13, 217–225. [Google Scholar] [CrossRef]
- Jain, A.; Satish, B. Clustering Based Short Term Load Forecasting Using Support Vector Machines. In Proceedings of the IEEE PowerTech Conference 2009, Bucharest, Romania, 28 June–2 July 2009; pp. 1–8.
- Lin, S.; Lee, Z.; Chen, S.; Tseng, T. Parameter determination of support vector machine and feature selection using simulated annealing approach. Appl. Soft Comput. 2008, 8, 1505–1512. [Google Scholar] [CrossRef]
- González, P.; Zamarreño, J. Prediction of hourly energy consumption in buildings based on a feedback artificial neural network. Energy Build. 2005, 37, 595–601. [Google Scholar] [CrossRef]
- Chakhchoukh, Y.; Panciatici, P.; Mili, L. New Robust Method Applied to Short-Term Load Forecasting. In Proceedings of the IEEE PowerTech Conference 2009, Bucharest, Romania, 28 June–2 July 2009; pp. 1–6.
- Fernández, I.; Borges, C.; Penya, Y. Efficient Building Load Forecasting. In Proceedings of the 16th IEEE International Conference on Emerging Technologies and Factory Automation (ETFA), Toulouse, France, 5–9 September 2011; pp. 1–8.
- Hibon, M.; Evgeniou, T. To combine or not to combine: Selecting among forecasts and their combinations. Int. J. Forecast. 2004, 21, 15–24. [Google Scholar] [CrossRef]
- Clemen, R. Combining forecasts: A review and annotated bibliography. Int. J. Forecast. 1989, 5, 559–583. [Google Scholar] [CrossRef]
- Borges, C.; Penya, Y.; Fernández, I. Optimal Combined Short-Term Building Load Forecasting. In Proceedings of the 2011 IEEE PES Innovative Smart Grid Technologies Asia, Perth, Australia, 13–16 November 2011; pp. 1–7.
- Dong, B.; Cao, C.; Lee, S. Applying support vector machines to predict building energy consumption in tropical region. Energy Build. 2005, 37, 545–553. [Google Scholar] [CrossRef]
- MacKay, D. Bayesian non-linear modelling for the prediction competition. ASHRAE Trans. 1994, 100, 1053–1062. [Google Scholar]
- Darbellay, G.; Slama, M. Forecasting the short-term demand for electricity—Do neural networks stand a better chance? Int. J. Forecast. 2000, 16, 71–83. [Google Scholar] [CrossRef]
- Soares, L.; Souza, L. Forecasting electricity demand using generalized long memory. Int. J. Forecast. 2006, 22, 17–28. [Google Scholar] [CrossRef]
- Wu, C.H.; Tzeng, G.H.; Lin, R.H. A novel hybrid genetic algorithm for kernel function and parameter optimization in support vector regression. Expert Syst. Appl. 2009, 36, 4725–4735. [Google Scholar] [CrossRef]
- Ismail, Z.; Jamaluddin, F. Time series regression model for forecasting Malaysian electricity load demand. Asian J. Math. Stat. 2008, 1, 139–149. [Google Scholar] [CrossRef]
- Ferreira, V.; Pinto-Alves-da Silva, A. Automatic Kernel Based Models for Short Term Load Forecasting. In Proceedings of the 15th International Conference on Intelligent System Applications to Power Systems (ISAP), Curitiba, Brazil, 8–12 November 2009; pp. 1–6.
- De Menezes, L.M.; Bunn, D.W.; Taylor, J.W. Review of guidelines for the use of combined forecasts. Eur. J. Oper. Res. 2000, 120, 10–204. [Google Scholar] [CrossRef]
- Scott-Armstrong, J. Combining forecasts: The end of the beginning or the beginning of the end. Int. J. Forecast. 1989, 5, 585–588. [Google Scholar] [CrossRef]
- Prudencio, R.; Ludermir, T. Using Machine Learning Techniques to Combine Forecasting Methods. In Proceedings of the 17th Australian Joint Conference on Advances in Artificial Intelligence, Cairns, Australia, 4–6 December 2004; pp. 1122–1127.
- Song, K.B.; Baek, Y.S.; Hong, D.H. Short-term load forecasting for the holidays using fuzzy linear regression method. IEEE Trans. Power Syst. 2005, 20, 96–101. [Google Scholar] [CrossRef]
- Jin, Y.X.; Su, J. Similarity Clustering and Combination Load Forecasting Techniques Considering the Meteorological Factors. In Proceedings of the 6th World Scientific and Engineering Academy and Society (WSEAS) International Conference on Instrumentation, Measurement, Circuits and Systems, Hangzhou, China, 15–17 April 2007; pp. 115–119.
- Cortez, P.; Rocha, M.; Neves, J. A Meta-Genetic Algorithm for Time Series Forecasting. In Proceedings of Workshop on Artificial Intelligence Techniques for Financial Time Series Analysis (AIFTSA-01), 10th Portuguese Conference on Artificial Intelligence (EPIA’01), Porto, Portugal, 17–20 December 2001; pp. 21–31.
- Wang, X.; Smith-Miles, K.; Hyndman, R. Rule induction for forecasting method selection: Meta-learning the characteristics of univariate time series. Neurocomputing 2009, 72, 2581–2594. [Google Scholar] [CrossRef]
- Chakhchoukh, Y.; Panciatici, P.; Bondon, P.; Mili, L. Robust Short-Term Load Forecasting Using Projection Statistics. In Proceedings of 3rd IEEE International Workshop on the Computational Advances in Multi-Sensor Adaptive Processing (CAMSAP), Aruba Island, Dutch Antilles, 13–16 December 2009; pp. 45–48.
- Penya, Y.K.; Nieves, J.C.; Espinoza, A.; Borges, C.E.; Peña, A.; Ortega, M. Distributed semantic architecture for smart grids. Energies 2012, 5, 4824–4843. [Google Scholar] [CrossRef]
- Penya, Y.; Borges, C.; Agote, D.; Fernandez, I. Short-Term Load Forecasting in Air-Conditioned Non-Residential Buildings. In Proceedings of the 20th IEEE International Symposium on Industrial Electronics (ISIE), Gdansk, Poland, 27–30 June 2011; pp. 1359–1364.
- Hsu, C.W.; Chang, C.C.; Lin, C.J. A Practical Guide to Support Vector Classification. 2010. Available online: http://www.csie.ntu.edu.tw/~cjlin/papers/guide/guide.pdf (accessed on 19 December 2012).
- Borges, C.; Penya, Y.; Fernández, I. Evaluating combined load forecasting in large power systems and smart grids. IEEE Trans. Ind. Inform. 2012. [Google Scholar] [CrossRef]
- Cristianini, N.; Shawe-Taylor, J. An Introduction to Support Vector Machines: And Other Kernel-Based Learning Methods, 1st ed.; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- International Electrotechnical Commission. IEC60870: Telecontrol Equipment and Systems-Part 5: Transmission Protocols-Section 102: Companion Standard for the Transmission of Integrated Totals in Electric Power Systems; IEC: Geneva, Switzerland, 1996. [Google Scholar]
- Kreider, J.; Haberl, J. Predicting hourly building energy usage: The great energy predictor shootout–Overview and discussion of results. ASHRAE Trans. 1994, 100, 1104–1118. [Google Scholar]
- Felice, M.D. Load, Weather and Occupancy Data for C59 ENEA Building. Available online: http://www.matteodefelice.name/research/resources/ (accessed on 21 December 2012).
- Cancelo, J.; Espasa, A.; Grafe, R. Forecasting the electricity load from one day to one week ahead for the Spanish system operator. Int. J. Forecast. 2008, 24, 588–602. [Google Scholar] [CrossRef]
- PJM Interconnection System Operator. Day-Ahead Scheduling Manual. Aviable online: http://www.pjm.com/sitecore%20modules/web/~/media/training/core-curriculum/ip-gen-201/gen-201-scheduling-process.ashx (accessed on 29 March 2013).
- New York Independent System Operator. Day-Ahead Scheduling Manual. Aviable online: http://www.nyiso.com/public/webdocs/markets_operations/documents/Manuals_and_Guides/Manuals/Operations/dayahd_schd_mnl.pdf (accessed on 29 March 2013).
- Eunite Competition Comite. Electricity Load Forecast using Inteligent Adaptative Technology. 2001. Available online: http://neuron.tuke.sk/competition/instructions.php (accessed on 19 April 2011).
- Arlot, S.; Celisse, A. A survey of cross-validation procedures for model selection. Stat. Surv. 2010, 4, 40–79. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Koehler, A.B. Another look at measures of forecast accuracy. Int. J. Forecast. 2006, 22, 679–688. [Google Scholar] [CrossRef]
- Chang, C.C.; Lin, C.J. LIBSVM: A library for support vector machines. ACM Trans. Intell. Syst. Technol. 2011, 2, 1–27. Available online: http://www.csie.ntu.edu.tw/~cjlin/libsvm (accessed on 29 March 2013). [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Borges, C.E.; Penya, Y.K.; Fernández, I.; Prieto, J.; Bretos, O. Assessing Tolerance-Based Robust Short-Term Load Forecasting in Buildings. Energies 2013, 6, 2110-2129. https://doi.org/10.3390/en6042110
Borges CE, Penya YK, Fernández I, Prieto J, Bretos O. Assessing Tolerance-Based Robust Short-Term Load Forecasting in Buildings. Energies. 2013; 6(4):2110-2129. https://doi.org/10.3390/en6042110
Chicago/Turabian StyleBorges, Cruz E., Yoseba K. Penya, Iván Fernández, Juan Prieto, and Oscar Bretos. 2013. "Assessing Tolerance-Based Robust Short-Term Load Forecasting in Buildings" Energies 6, no. 4: 2110-2129. https://doi.org/10.3390/en6042110
APA StyleBorges, C. E., Penya, Y. K., Fernández, I., Prieto, J., & Bretos, O. (2013). Assessing Tolerance-Based Robust Short-Term Load Forecasting in Buildings. Energies, 6(4), 2110-2129. https://doi.org/10.3390/en6042110