Next Article in Journal
Comparative Study of Dynamic Programming and Pontryagin’s Minimum Principle on Energy Management for a Parallel Hybrid Electric Vehicle
Previous Article in Journal
Energy Management and Smart Grids
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Energies
Volume 6
Issue 4
10.3390/en6042291
energies-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Effect of Burnable Absorbers on Inert Matrix Fuel Performance and Transuranic Burnup in a Low Power Density Light-Water Reactor

by
Geoff Recktenwald
and
Mark Deinert
*
Department of Mechanical Engineering, The University of Texas at Austin, 1 University Station C2200, Austin, TX 78715-0162, USA
*
Author to whom correspondence should be addressed.
Energies 2013, 6(4), 2291-2304; https://doi.org/10.3390/en6042291
Submission received: 21 January 2013 / Revised: 20 March 2013 / Accepted: 4 April 2013 / Published: 22 April 2013
Browse Figures
Versions Notes

Abstract

:
Zirconium dioxide has received particular attention as a fuel matrix because of its ability to form a solid solution with transuranic elements, natural radiation stability and desirable mechanical properties. However, zirconium dioxide has a lower coefficient of thermal conductivity than uranium dioxide and this presents an obstacle to the deployment of these fuels in commercial reactors. Here we show that axial doping of a zirconium dioxide based fuel with erbium reduces power peaking and fuel temperature. Full core simulations of a modified AP1000 core were done using MCNPX 2.7.0. The inert matrix fuel contained 15 w/o transuranics at its beginning of life and constituted 28% of the assemblies in the core. Axial doping reduced power peaking at startup by more than ~23% in the axial direction and reduced the peak to average power within the core from 1.80 to 1.44. The core was able to remain critical between refueling while running at a simulated 2000 MWth on an 18 month refueling cycle. The results show that the reactor would maintain negative core average reactivity and void coefficients during operation. This type of fuel cycle would reduce the overall production of transuranics in a pressurized water reactor by 86%.

Graphical Abstract

1. Introduction

The environmental and geopolitical problems that are associated with nuclear power stem in part from the accumulation of the transuranics Am, Cm, Np and Pu in used nuclear fuel [1]. By limiting the production of these four elements many of the concerns that surround the future development of nuclear energy would be significantly reduced. This fact has been known within the nuclear engineering community for decades, and several methods for transmuting these transuranics into more benign forms have been proposed [2,3,4,5,6]. At present, the only option for recycling any of the transuranics is to use commercial reprocessing [7,8] mix plutonium and uranium oxides to produce a mixed oxide fuel that can be used in a conventional reactor. However, due to neutron capture in the uranium, these fuels also produce transuranics while in the reactor, and are only somewhat effective at limiting their production [5,9].
An alternative to mixed oxide recycle is to entrain the transuranics in a uranium free matrix. The thorium fuel cycle is an example of this. Here energy comes from the fission of 233U which is bred in by neutron capture in the thorium. However, 233U poses a significant proliferation risk and in practice 238U would be added to the fuel to dilute it [3,10]. However, the presence of uranium in fuel again results in the production of the transuranics that one is trying to get rid of. Another option that has been explored is to blend the transuranics into a zirconium dioxide matrix, Figure 1.
Energies 06 02291 g001 1024
Figure 1. The inert matrix fuel cycle. Spent fuel from a conventional light-water reactor would be reprocessed and the transuranics Am, Cm, Np and Pu stripped, and blended with a uranium free matrix. The resulting fuel would be placed back into the light-water reactor. Because it contains no uranium, the inert matrix fuel form allows for the consumption of transuranic waste without any additional production. The inert matrix fuel would also reduce the overall amount of uranium in the core. The percentage of the core that is uranium dioxide (UOX) or inert matrix fuel (IMF) is a design parameter.
Figure 1. The inert matrix fuel cycle. Spent fuel from a conventional light-water reactor would be reprocessed and the transuranics Am, Cm, Np and Pu stripped, and blended with a uranium free matrix. The resulting fuel would be placed back into the light-water reactor. Because it contains no uranium, the inert matrix fuel form allows for the consumption of transuranic waste without any additional production. The inert matrix fuel would also reduce the overall amount of uranium in the core. The percentage of the core that is uranium dioxide (UOX) or inert matrix fuel (IMF) is a design parameter.
Energies 06 02291 g001
Fuels such as these were originally proposed for burning down stockpiles of weapons plutonium [11,12], but can also be for efficient transmutation in light-water reactors [5,9]. The lack of uranium in the fuel allows for theconsumption of transuranics without any additional production, hence the term “inert”. Because of its mechanical properties and radiation hardness, zirconium dioxide based fuel has received considerable attention in the past decade and have gone through initial testing at high flux test facilities with good results [4,13,14,15,16,17,18].
The energy produced by nuclear fuel is expressed in terms of “burnup” which has units of MWd/kgIHM, where IMH is the initial heavy metal present in the fuel when it is loaded into the reactor. Since the transuranics represent the only heavy metal in an inert matrix fuel, all of this energy would come from their consumption. Previous work has shown that a burnup of 750 MWd/kgIHM, which corresponds to ~80% transuranic consumption, may present a practical limit for zirconium dioxide based fuel [19,20]. However, achieving this level of burnup in a real reactor would require a relatively high transuranic content in the fresh fuel if the reactor were to remain critical between loadings and recycle its own transuranics. Unfortunately, high transuranic content can result in a high power density. This presents a particular problem for a zirconium dioxide based fuel because of the material’s low coefficient of thermal conductivity [21,22].
Past work with uranium dioxide fuels has shown that burnable absorbers can be used to reduce power and temperature. Common methods for doing this include the addition of gadolinium and erbium oxides to the fuel or the use of a thin zirconium boride coating (e.g. [23,24]) and these poisons are often referred to as ‘integral burnable absorbers’ because they are integral to the fuel. In the current contribution we show that burnable absorbers can be used with zirconium dioxide based fuel to help keep the reactor, and the fuel, within licensable limits.

2. Methods

2.1. Overview

We consider a modified AP1000 [25] pressurized water reactor with both inert matrix and uranium dioxide fuels in assemblies in 8 × 8 square lattices. The uranium assemblies help to maintain criticality between refuelings while the inert matrix fuels are used to burn the transuranics present in the spent uranium fuel. Full core simulations were done using MCNPX 2.7.0 [26], a Monte Carlo radiation transport code, to determine the pin and assembly power profiles. The change in isotopic composition was determined using the CINDER90 burn card and verified with an in-house collision probability code [26]. The results of the Monte Carlo simulations were coupled to a steady state thermal transport model to compute peak fuel and cladding temperatures using thermal resistances for the materials and the coolant [27]. These temperatures were then fed back into MCNPX to capture thermal effects on reactor performance. The simulated reactor core had a power of 2000MWth and ran on a standard 18 month refueling schedule that would be encountered with current generation light-water reactors.

2.2. Monte Carlo Simulations and Fuel Composition

The uranium dioxide fuel was enriched to 5% 235U, burned to 42 MWd/kgIHM, and run through the core in three campaigns so that 1/3 would be removed and replaced at refueling every 18 months. Once removed, the fuel was allowed to cool for a simulated 5 years. The resulting transuranic vector was used as an input for the formulation of the simulated inert matrix fuel, which had 15w/o transuranics at its beginning of life in the core. The inert matrix fuel was run in seven campaigns, so that 1/7 was removed every 18 months. The total residence time for the inert matrix assemblies was 10.5 years and 4.5 years for the uranium dioxide assemblies. Table 1 gives the reactor parameters used in the Monte Carlo simulations with Figure 2 showing a 1/8 cross sectional view of the core and the layout of the uranium and inert matrix assemblies.
Table
Table 1. Fuel assembly parameters.
Table 1. Fuel assembly parameters.
ParameterValue
Fuel pin radius0.396cm
Pin pitch1.3 cm
Pin height426.7 cm
Cladding thickness0.05 cm
CladdingZircalloy
Gap thickness0.02 cm
Lattice size8 pin × 8 pin
Number of fuel pins per assembly60
Number of guide tubes per assembly4
Active Core diameter325 cm
Uranium fuel density11g/cm3
Inert matrix fuel density5.75 g/cm3 (doped)
Pressure vessel inner diameter401.6 cm
Pressure vessel thickness20 cm
Energies 06 02291 g002 1024
Figure 2. Fuel assembly configuration. (left) Schematic of an 8 × 8 fuel assembly with 60 fuel pins and 4 guide tubes; (right) The assembly layout of the reactor was designed with 8-fold symmetry. Here the Ux and Ix represent the xth campaigns of uranium fuel and inert matrix fuel assemblies. A center assembly is left empty (moderator region). Each fuel assembly is 8 × 8 with 4 control rod guide tubes and 60 fuel pins.
Figure 2. Fuel assembly configuration. (left) Schematic of an 8 × 8 fuel assembly with 60 fuel pins and 4 guide tubes; (right) The assembly layout of the reactor was designed with 8-fold symmetry. Here the Ux and Ix represent the xth campaigns of uranium fuel and inert matrix fuel assemblies. A center assembly is left empty (moderator region). Each fuel assembly is 8 × 8 with 4 control rod guide tubes and 60 fuel pins.
Energies 06 02291 g002
Uranium dioxide fuel pins were doped axially with boron oxide and the inert matrix pins with erbium oxide. In each case the pins were divided into five axial regions, Figure 3. The concentration of boron and erbium was varied in these regions to reduce power peaking. The concentration of boron in regions 1 and 5 was 0 w/o, in regions 2 and 4 it was 2.55 × 10−4 w/o, and in region 3 it was 3.27 × 10−4 w/o boron respectively. The concentration of erbium in the same regions was 0 w/o, 1.70 × 10−2 w/o, and 2.18 × 10−2 w/o respectively. These concentrations follow the method outlined in [23]. Table 3 shows the resulting composition of the uranium and inert matrix fuels at beginning of life. Natural boron and erbium were used.
Energies 06 02291 g003 1024
Figure 3. Axial distribution of burnable absorber in fuel. The uranium dioxide fuel was doped with boron and the inert matrix fuel with erbium oxide, both of which absorb neutrons and reduce the power output of the pin. Over time, both the born and the erbium burn out.
Figure 3. Axial distribution of burnable absorber in fuel. The uranium dioxide fuel was doped with boron and the inert matrix fuel with erbium oxide, both of which absorb neutrons and reduce the power output of the pin. Over time, both the born and the erbium burn out.
Energies 06 02291 g003
In all simulations the composition of the uranium and inert matrix fuels were equilibrated to reflect the isotopes that would be encountered in a real reactor containing fuel at various degrees of burnup. This was done by iterating on the fuel composition until the end of life fuel composition in campaign j was identical to the beginning of life composition in campaign j + 1 fuel for each fuel form and age of fuel, Equation (1):
MaterialVectorCampaign = j + 1(t) = MaterialVectorCampaign = j(t + ΔtCampaign)
The fraction of the core that is comprised of inert matrix fuel was chosen under the constraint that the core reactivity remain > 1 between refueling, and that the reactor can recycle the transuranics from its own spent uranium fuel [19]. The simulated cores have 712, 8 × 8 assemblies, where 516 are uranium dioxide fuel. This is equivalent to a 178 assembly core of 16 × 16 assemblies. Additional details on the reactor geometry and equilibrated composition of the fuel can be found in the supplemental information.

2.3. Thermal Transport

The peak fuel and outer cladding temperatures were determined using a steady state thermal transport model:
Energies 06 02291 i001
where q’ is the linear power density of the fuel W/m; ∆T is the temperature difference between two points; and R is the respective resistance. The linear power density was determined using the MCNPX simulations. The temperature of the moderator along a coolant channel was determined using Newton’s law of cooling and the temperature dependent heat capacity of water. It was assumed that the power density of the fuel varied only axially, not radially. Table 2 gives the thermal transport parameters that were assumed for the uranium and zirconium dioxide as well as the cladding, gap and coolant. Additional details on the equations used in computing the temperature of the fuel and moderator can be found in the supplemental information.
Table
Table 2. Thermal transport parameters.
Table 2. Thermal transport parameters.
PropertyLocationValueReference
Thermal conductivityUranium dioxide fuel2.9 W/m-K[28], SI
Inert matrix fuel1.8 W/m-K[29], SI
Cladding20.0 W/m-K[27]
Convective heat transfer coefficientAir gap5,679 W/m2-K[27]
Moderator16,600 W/m2-KSI
Coolant flow ratePer channel0.384 kg/sec*
TemperatureInlet550 K*
Notes: * These values are consistent with existing pressurized water reactors and were chosen to keep the simulated reactor within operational limits; SI is supplemental information.
Figure 4 shows the average linear power density immediately at startup after refueling, both with and without the addition of burnable absorber along with the axial temperature profile for the hottest uranium and inert matrix fuel pins.

2.4. Reactivity Coefficients

The reactivity coefficients were computed using static calculations in MCNPX 2.7.0 at various times during the simulated 18 month burnup cycle. The fuel, moderator, and void coefficients of reactivity were computed at the full core and assembly level using reactor simulations of the full core. We used makxs [26] to create a higher resolution MCNPX library with temperature dependent cross sections built in 10 K intervals from 300 K to 610 K and in 50 K intervals from 650 K to 2500 K.
The coefficient of thermal reactivity for the fuel was computed by perturbing the temperature of the fuel in the reactor by ±50 K. The coefficients were computed using [30]:
Energies 06 02291 i002
Energies 06 02291 g004 1024
Figure 4. Effect of burnable absorber. The axial power profile and temperatures are shown at startup for the beginning of life uranium and hottest inert matrix fuel assemblies. Axial grading reduces the power peaking by more than 5% and lowers the inert matrix fuel maximum temperature by 200 K.
Figure 4. Effect of burnable absorber. The axial power profile and temperatures are shown at startup for the beginning of life uranium and hottest inert matrix fuel assemblies. Axial grading reduces the power peaking by more than 5% and lowers the inert matrix fuel maximum temperature by 200 K.
Energies 06 02291 g004
Fuel reactivity coefficients for all of the fuel assemblies (uranium dioxide and inert matrix) were found to be negative both at startup and at the end of cycle before shutting down for refueling. Plots of the reactivity coefficients can be found in the supplemental information.
The core average moderator coefficient of reactivity was computed by modeling the full core for a range of core average moderator temperatures. The moderator density was updated to match saturated liquid water tables at a pressure of 155 bar. The coefficients were computed using [30]:
Energies 06 02291 i003
Figure 5 shows the core averaged moderator coefficients as a function of the temperature of the moderator at the beginning and end of the campaign. The core average void coefficients were computed using [30]:
Energies 06 02291 i004
Here x is the core average void fraction, and is computed by decreasing the fluid density uniformly within the core. Figure 6 shows the core average void coefficients of reactivity for a set of void percentages at the beginning and end of the campaign. At zero void, the beginning of cycle and end of cycle void reactivity coefficients were found to be −1.67 × 10−3 (1/K) and −1.58 × 10−3 (1/K), respectively.
Assembly level reactivity coefficients have been computed and are included in the supplemental material. The errors bars on Figure 5 and Figure 6 were generated from ten simulations, each done with different initial seeds. The error bars then indicate the range about the mean value.
Energies 06 02291 g005 1024
Figure 5. Moderator Thermal Reactivity Coefficients. The reactivity coefficients of the moderator are shown for a range of temperatures at the beginning and end of campaign. The reactor coefficients at the beginning and end of campaign are −3.77 × 10−4 ± 6.9 × 10−6 (1/K) and −3.27 × 10−4 ± 6.1 × 10−6 (1/K) respectively.
Figure 5. Moderator Thermal Reactivity Coefficients. The reactivity coefficients of the moderator are shown for a range of temperatures at the beginning and end of campaign. The reactor coefficients at the beginning and end of campaign are −3.77 × 10−4 ± 6.9 × 10−6 (1/K) and −3.27 × 10−4 ± 6.1 × 10−6 (1/K) respectively.
Energies 06 02291 g005
Energies 06 02291 g006 1024
Figure 6. Void Reactivity Coefficients. The reactivity coefficient of a moderator void is shown for a range of core averaged voids. At 10% void fraction the reactivity coefficients at the beginning and end of campaign are −0.00185 ± 1.3 × 10−5 (1/K) and −0.00179 ± 1.1 × 10−5 (1/K) respectively.
Figure 6. Void Reactivity Coefficients. The reactivity coefficient of a moderator void is shown for a range of core averaged voids. At 10% void fraction the reactivity coefficients at the beginning and end of campaign are −0.00185 ± 1.3 × 10−5 (1/K) and −0.00179 ± 1.1 × 10−5 (1/K) respectively.
Energies 06 02291 g006

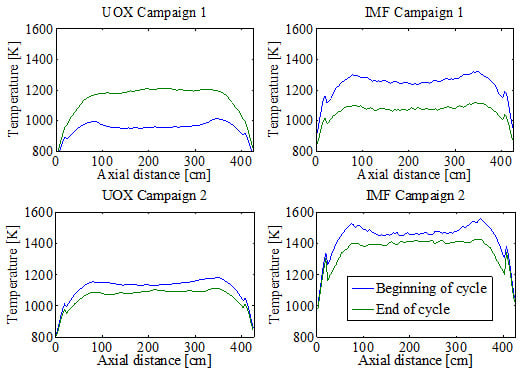
3. Results and Discussion

Figure 7 and Figure 8 show the power and thermal profiles for the hottest uranium and inert matrix fuel elements with and without doping. The temperature profiles in Figure 4 and Figure 8 differ because the data in Figure 8 correspond to shortly after startup when the xenon and samarium fission products (which absorb neutrons) have come to secular equilibrium. The data in Figure 4 are from directly after startup and the xenon and samarium have not built up.
Energies 06 02291 g007 1024
Figure 7. Axial power profile. The linear power of the hottest 4 assemblies are shown at the beginning and end of cycle.
Figure 7. Axial power profile. The linear power of the hottest 4 assemblies are shown at the beginning and end of cycle.
Energies 06 02291 g007
Energies 06 02291 g008 1024
Figure 8. Axial temperature profile. The axial temperatures of the four assemblies in Figure 7 at the beginning and end of cycle.
Figure 8. Axial temperature profile. The axial temperatures of the four assemblies in Figure 7 at the beginning and end of cycle.
Energies 06 02291 g008
The hottest fuel assemblies are those in the second campaigns since the doping has largely burned out by this point. As can be seen, the use of an integral burnable absorber significantly flattens the power and thermal profiles in both the uranium and inert matrix fuels. Peak linear power density in the inert matrix fuel was reduced by 23% with a 15% decrease in peak temperature. While zirconium dioxide has a melting point of ~2715 °C, in pile testing has shown that fission gas release from zirconium dioxide fuels increases significantly with elevated temperatures [15,31], but at the temperatures shown it would be more comparable to uranium dioxide fuels.
The addition of the integral burnable poisons has the beneficial effect of significantly flattening the radial power distribution as well. Figure 9 shows a cross sectional view of the average linear power density in the core at the assembly level at the beginning of cycle, end of cycle, and the average over an 18 month period between refueling. As can be seen in Figure 9d, there is a significant change in the linear power density between the hottest and coolest assemblies which is attributable to the high degree of transuranic burnout in the inert matrix fuels. Figure 10 shows the time dependent linear power density in each campaign and more detail is included in the supplemental material. As can be seen, most of the power is derived from the uranium assemblies and the first three campaigns of inert matrix fuel. The last four inert matrix fuel campaigns act as net neutron absorbers.
Energies 06 02291 g009 1024
Figure 9. Radial core power profile. The power distribution within the core assemblies is shown for the (a) end of campaign; (b) beginning of campaign; (c) minimum values and (d) maximum values.
Figure 9. Radial core power profile. The power distribution within the core assemblies is shown for the (a) end of campaign; (b) beginning of campaign; (c) minimum values and (d) maximum values.
Energies 06 02291 g009
Energies 06 02291 g010 1024
Figure 10. Assembly level power. The power from each assembly within the core changes over the course of the campaign.
Figure 10. Assembly level power. The power from each assembly within the core changes over the course of the campaign.
Energies 06 02291 g010
A requirement for a licensable reactor in the US is that it maintain negative core average moderator and void reactivity coefficients [30]. Figure 5 and Figure 6 showed the core average moderator and void reactivity coefficients immediately after starting up and immediately before shutting down to refuel. Importantly, these coefficients remain negative between refuelings. It should be pointed out that while the assembly level reactivity coefficients are negative for the fuel, they are not uniformly negative for the moderator and void at the assembly level. Additional details on reactivity coefficients at the assembly level are included in the supplemental material.
A remarkable feature of the results presented here is the high degree of burnup that is achieved in the inert matrix fuel by the time it is removed from the core. The inert matrix fuel experienced a burnup of ~780 MWd/kgIHM, which corresponds to an 84% burnout of the transuranics. Noteably, the only heavy metal in an inert matrix fuel comes from the transuranics and this degree of burnup would be equivalent to burning a uranium dioxide fuel to ~60 MWd/kgIHM. Despite this, the core maintains a Keff > 1.008 in between refuelings, Figure 11, and the 8 × 8 fuel assemblies play an important role here. The small assemblies allow for a more even distribution of the low reactivity fuel assemblies (late stage inert matrix fuel) and a reduction in the power variations across an assembly. Additionally, the inert matrix assemblies have a fixed composition at the beginning of their life in the core. Ideally the transuranic content of the beginning of life inert matrix fuel assemblies will exactly match the transuranic content of the end of life uranium assemblies. This is impossible since the reactor has an integer number of assemblies. However, for a fixed core size, reducing the size of the assemblies will increase the total number of assemblies and allow for a closer match.
The cost for the high transuranic depletion is a reduction in core operating power. The simulations discussed here were done with a nominal reactor power of 2000 MWth, which is two thirds of that for a conventional AP1000. Operation at a higher power would cause an earlier depletion of the uranium driver assemblies and the simulated reactor would not be able to operate on an 18 month cycle. The power could be increased to a more conventional value if the uranium fuel were enriched beyond 5% or if the refueling schedule were increased to a higher frequency than once every 18 months. Both possibilities will be the subject of future work.
Energies 06 02291 g011 1024
Figure 11. Reactor Criticality. The reactor criticality must be above 1 at the end of the campaign. This figure shows the drop in Keff over the campaign. For these simulations Keff = 1.008 ± 0.001 at end of cycle.
Figure 11. Reactor Criticality. The reactor criticality must be above 1 at the end of the campaign. This figure shows the drop in Keff over the campaign. For these simulations Keff = 1.008 ± 0.001 at end of cycle.
Energies 06 02291 g011

4. Conclusions

In the present study we show that integral burnable absorbers can be used in a mixed core running both inert matrix and uranium dioxide fuels to keep the fuel temperatures, and reactivity coefficients, within allowable limits. Erbium oxide was used with the inert matrix fuel and integral boron oxide with the uranium fuel. The integral burnable absorbers were shown to reduce axial power peaking by more than 23% and to reduce the peak to average power within the core from 1.80 to 1.44. By the end of its life in the core the inert matrix fuel acts as a neutron absorber with 84% of its initial transuranic inventory depleted. Importantly, the simulated core remains critical between refueling while running at a simulated power of 2000 MWth.
The axial thermal and power profiles in the fuel can be reduced to acceptable levels with the use of an integral burnable absorber and this has the additional benefit of flattening the core power profiles. Importantly, the simulations show that the reactivity coefficients in the various fuel types are all negative and that the core average moderator and void coefficient are negative as well, which are requirements for a commercial power reactor in the US. The results demonstrate that inert matrix fuels could be used in conventional pressurized water reactors to achieve significant reductions in the overall production transuranics.

Acknowledgements

This work was supported by Department of Energy NEUP contract 00128532. Special thanks to the staff at the Texas Advanced Computing Center (TACC) at The University of Texas at Austin and to Andrew Osborne for suggestions and discussions.

References

  1. Von Hippel, F.N. Energy—Plutonium and reprocessing of spent nuclear fuel. Science 2001, 293, 2397–2398. [Google Scholar] [CrossRef] [PubMed]
  2. Richter, B.; Hoffman, D.C.; Mtingwa, S.K.; Omberg, R.P.; Pillon, S.; Rempe, J.L. Report of Advanced Nuclear Transformation Technology Subcommittee of the Nuclear Energy Research Advisory Committee; Technical Reprot; Department of Energy: Washington, DC, USA, 2004.
  3. Herring, J.S.; MacDonald, P.E.; Weaver, K.D. Thorium-based transmuter fuels for light water reactors. Nucl. Technol. 2004, 147, 84–101. [Google Scholar]
  4. Kasemeyer, U.; Hellwig, C.; Lebenhaft, J.; Chawla, R. Comparison of various partial light water reactor core loadings with inert matrix and mixed-oxide fuel. J. Nucl. Mater. 2003, 319, 142–153. [Google Scholar] [CrossRef]
  5. Schneider, E.A.; Deinert, M.R.; Cady, K.B. Burnup simulations and spent fuel characteristics of ZrO2 based inert matrix fuels. J. Nucl. Mater. 2007, 361, 41–51. [Google Scholar] [CrossRef]
  6. Tulenko, J.S.; Wang, J.; Acosta, C. The Optimum Plutonium Inert Matrix Fuel Form for Reactor-Based Plutonium Disposition. In Proceedings of the ANES/SENA 2004 Symposium, American Nuclear Society, Miami Beach, FL, USA, 3–6 October 2004.
  7. Recktenwald, G.R.; Deinert, M.R. A cost probability analysis of reprocessing spent nuclear fuel in the us. Energy Econ. 2012, 34, 1873–1881. [Google Scholar] [CrossRef]
  8. Schneider, E.A.; Deinert, M.R.; Cady, B. The cost impact of delaying the us spent nuclear fuel reprocessing facility. Energy Econ. 2009, 31, 627–634. [Google Scholar] [CrossRef]
  9. Schneider, E.A.; Deinert, M.R.; Cady, K.B. Burnup Simulations of an Inert Matrix Fuel Using a Two Region, Multi-Group Reactor Physics Model, the Physics of Advanced Fuel Cycles. In Proceedings of PHYSOR 2006, Vancouver, BC, Canada, 10–14 September 2006.
  10. Herring, J.S.; MacDonald, P.E.; Weaver, K.D.; Kullberg, C. Low cost, proliferation resistant, uranium-thorium dioxide fuels for light water reactors. Nucl. Eng. Des. 2001, 203, 65–85. [Google Scholar] [CrossRef]
  11. Lombardi, C.; Cerrai, E. Buring Weapon-Grade in Ad Hoc Designed Reactors? In Proceedings of International Symposium on Conversion of Nuclear Warheads for Peaceful Purposes, Rome, Italy, 15–17 June 1992.
  12. Lombardi, C.; Mazzola, A. Exploiting the plutonium stockpiles in pwrs by using inert matrix fuel. Ann. Nucl. Energy 1996, 23, 1117–1126. [Google Scholar] [CrossRef]
  13. Degueldre, C.; Hellwig, C. Study of a zirconia based inert matrix fuel under irradiation. J. Nucl. Mater. 2003, 320, 96–105. [Google Scholar] [CrossRef]
  14. Hellwig, C.; Kasemeyer, U. Inert matrix fuel performance during the first two irradiation cycles in a test reactor: Comparison with modeling results. J. Nucl. Mater. 2003, 319, 87–94. [Google Scholar] [CrossRef]
  15. Hellwig, C.; Kasemeyer, U.; Ledergerber, G.; Lee, B.H.; Lee, Y.W.; Chawla, R. Interpretation of experimental results from moderate-power in-pile testing of a pu-er-zr-oxide inert matrix fuel. Ann. Nucl. Energy 2003, 30, 287–299. [Google Scholar] [CrossRef]
  16. Hellwig, C.; Pouchon, M.; Restani, R.; Ingold, F.; Bart, G. Fabrication and microstructure characterization of inert matrix fuel based on yttria stabilized zirconia. Ann. Nucl. Energy 2005, 340, 163–170. [Google Scholar]
  17. Kamel, N.; Ait-Amar, H.; Taouinet, M.; Benazzouz, C.; Kamel, Z.; Fodil-Cherif, H.; Telmoune, S.; Slimani, R.; Zahri, A.; Sahel, D. Comparative study of simulated zirconia inert matrix fuel stabilized with yttrium, lanthanum or praseodymium: Synthesis and leaching tests. Prog. Nucl. Energy 2006, 48, 70–84. [Google Scholar] [CrossRef]
  18. Kasemeyer, U.; Paratte, J.M.; Grimm, P.; Chawla, R. Comparison of pressurized water reactor core characteristics for 100% plutonium-containing loadings. Nucl. Technol. 1998, 122, 52–63. [Google Scholar]
  19. Recktenwald, G.; Deinert, M.R. Actinide transmutation using with deep burn in an inert matrix fuel. Trans. Am. Nucl. Soc. 2010, 102, 145–146. [Google Scholar]
  20. Schneider, E.A.; Deinert, M.R. A Practical Limit for Actinide Transmutation in Intert Matrix Fuels. In Proceedings of the International Conference on the Physics of Reactors 2008 PHYSOR, Interlaken, Switzerland, 14–19 September 2008.
  21. Medvedev, P.G.; Frank, S.M.; O’Holleran, T.P.; Meyer, M.K. Dual phase MgO-ZrO2 ceramics for use in lwr inert matrix fuel. J. Nucl. Mater. 2005, 342, 48–62. [Google Scholar] [CrossRef]
  22. Sobolev, V.; Lemehov, S. Modelling heat capacity, thermal expansion, and thermal conductivity of dioxide components of inert matrix fuel. J. Nucl. Mater. 2006, 352, 300–308. [Google Scholar] [CrossRef]
  23. Segrev, M. Use of axially graded burnable boron for hot-spot temperature reduction in a pressurized water reactor core. J. Nucl. Mater. 2000, 135, 280–287. [Google Scholar]
  24. O’Leary, P.M.; Pitts, M.L. Effects of Burnable Absorbers on PWR Spent Nuclear Fuel. In Proceedings of Waste Management 2001 Conference, Tucson, AZ, USA, 25 Febuary–1 March 2001.
  25. The Westinghouse AP1000 Advanced Nuclear Plant; Westinghouse Electric Company LLC: Butler, PA, USA, 2003; p. 17.
  26. Pelowitz, D.B.; Durkee, J.W.; Elson, J.S.; Fensin, M.L.; James, M.R.; Johns, R.C.; McKinney, G.W.; Mashnik, S.G.; Wasters, L.S.; Wilcox, T.A.; et al. Mcnpx User's Manual Version 2.7.0; LA-CP-11-00438; Los Alamos National Laboratory: Los Alamos, NM, USA, 2011. [Google Scholar]
  27. Lamarsh, J.R. Introduction to Nuclear Engineering, 3rd ed.; Prentice-Hall: Upper Saddle River, NJ, USA, 2001. [Google Scholar]
  28. Popov, S.G.; Carbajo, J.J.; Ivanov, V.K.; Yoder, G.L. Thermophysical Properties of Inert Matrix Fuels for Actinide Transmutation; Technical Report ORNL/TM-2000/351; Oak Ridge National Laboratory: Oak Ridge, TN, USA, 2000. [Google Scholar]
  29. Ronochi, C.; Ottaviani, J.P.; Degueldre, C.; Calabrese, R. Thermophysical properties of inert matrix fuels for actinide transmutation. J. Mater. Res. 2003, 320, 54–65. [Google Scholar]
  30. Power Plant Engineering Course Manual; United States Nuclear Regulatory Commission Technical Training Center: Washington, DC, USA, 1995. Available online: http://pbadupws.nrc.gov/docs/ML0230/ML023020604.pdf (accessed on 19 April 2013).
  31. Hellwig, C.; Streit, M.; Blair, P.; Tverberg, T.; Klaassen, F.C.; Schram, R.P.C.; Vettraino, F.; Yamashita, T. Inert matrix fuel behavior in test irradiations. J. Nucl. Mater. 2006, 352, 291–299. [Google Scholar] [CrossRef]

Share and Cite

MDPI and ACS Style

Recktenwald, G.; Deinert, M. Effect of Burnable Absorbers on Inert Matrix Fuel Performance and Transuranic Burnup in a Low Power Density Light-Water Reactor. Energies 2013, 6, 2291-2304. https://doi.org/10.3390/en6042291

AMA Style

Recktenwald G, Deinert M. Effect of Burnable Absorbers on Inert Matrix Fuel Performance and Transuranic Burnup in a Low Power Density Light-Water Reactor. Energies. 2013; 6(4):2291-2304. https://doi.org/10.3390/en6042291

Chicago/Turabian Style

Recktenwald, Geoff, and Mark Deinert. 2013. "Effect of Burnable Absorbers on Inert Matrix Fuel Performance and Transuranic Burnup in a Low Power Density Light-Water Reactor" Energies 6, no. 4: 2291-2304. https://doi.org/10.3390/en6042291

APA Style

Recktenwald, G., & Deinert, M. (2013). Effect of Burnable Absorbers on Inert Matrix Fuel Performance and Transuranic Burnup in a Low Power Density Light-Water Reactor. Energies, 6(4), 2291-2304. https://doi.org/10.3390/en6042291

Article Metrics

Back to TopTop