Comparison and Impact of Waste Heat Recovery Technologies on Passenger Car Fuel Consumption in a Normalized Driving Cycle
Abstract
:1. Introduction

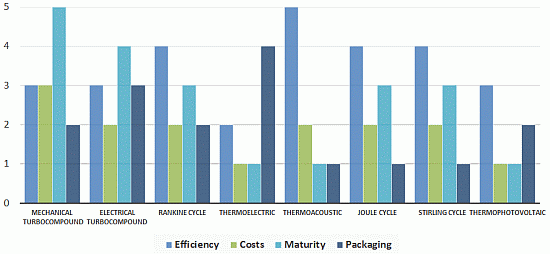
2. Waste Heat Recovery Technologies: Complete State of the Art


3. Modeling of Various Waste Heat Recovery Technologies
3.1. Rankine Cycle


3.2. Thermoelectricity

3.3. Turbocompound
4. Simulations of the Various Waste Heat Recovery Technologies
4.1. Simulation Parameters

| Additional parameters | Rankine cycle | Thermoelectricity | Turbocompound |
|---|---|---|---|
| Additional weight (kg) | 20 | 10 | 10 |
| Converter efficiency (%) | 90 | – | 90 |
4.2. Simulation Results



5. Conclusions
Author Contributions
Nomenclature
Symbols
| Boiling number | – | |
| Constant | – | |
| Minimum capacitive flow rate | J/s.K | |
| Constant pressure specific heat capacity | J/kg.K | |
| Hydraulic diameter | M | |
| Specific enthalpy | J/kg.K | |
| Heat transfer coefficient | W/m²K | |
| Thermal conductivity | W/mK | |
| Mass flow rate | Kg/s | |
| Number of transfer units | – | |
| Prandtl number | – | |
| Heat transfer rate | W | |
| Thermal resistance | m2K/W | |
| Reynolds number | – | |
| Temperature | K | |
| Power | W | |
| Mean figure of merit | – |
Subscripts
| 1P | One phase |
| 2P | Two phases |
| Cold | Cold side |
| Coolant | Coolant side |
| Ex | Exhaust |
| Gas | Gas side |
| Hot | Hot side |
| Is | Isentropic |
| Pp | Pump |
| Su | Supply |
| wf | Working fluid side |
Greek letters
| Heat capacity ratio | – | |
| Effectiveness | – | |
| Efficiency | – | |
| Capacitive mass flow rate ratio | – |
Conflicts of Interest
References
- Daccord, R.; Melis, J.; Kientz, T.; Darmedru, A.; Pireyre, R.; Brisseau, N.; Fonteneau, E. Exhaust heat recovery with rankine piston expander. In Proceedings of ICE Powertrain Electrification & Energy Recovery, Rueil-Malmaison, France, 28 May 2013.
- Mexico Light-Duty Vehicle CO2 and Fuel Economy Standards; International Council On Clean Transportation: Berlin, Germany, 2012.
- Borgne, G.L. Le Véhicule 2L/100km: Un Grand Programme D'avenir Mobilisateur; Ateliers de la filière automobile: Paris, France, 2013. (In French) [Google Scholar]
- Chammas, R.E.; Clodic, D. Combined cycle for hybrid vehicles. In Proceedings of SAE World Congress, Detroit, MI, USA, 11–14 April 2005.
- Conklin, J.C.; Szybist, J.P. A highly efficient six-stroke internal combustion engine cycle with water injection for in-cylinder exhaust heat recovery. Engery 2010, 35, 1658–1664. [Google Scholar]
- Endo, T.; Kawajiri, S.; Kojima, Y.; Takahashi, K.; Baba, T.; Ibaraki, S.; Takahashi, T.; Shinohara, M. Study on maximizing exergy in automotive engines. SAE Technical Paper 2007. [Google Scholar] [CrossRef]
- Gardner, D.L.; Howard, C.Q. Waste-heat-driven thermoacoustic engine and refrigerator. In Proceedings of Acoustics 2009, Adelaide, Australia, 23–25 November 2009.
- Fu, J.; Liu, J.; Yang, Y.; Ren, C.; Zhu, G. A new apporach for exhaust energy recovery of internal combustion engine: Steam turbocharging. Appli. Therm. Eng. 2013, 52, 150–159. [Google Scholar] [CrossRef]
- Sirot, F. Les moteurs à cycles asymétriques, une approche énergétique efficiente en phase avec les nouveaux enjeux technico-économiques: Cas du moteur 5 temps SWG. In Proceedings of Utilisation rationnelle de l'énergie et environnement, Paris, France, 26 March 2013. (In French)
- Douglas-self. The Kitson-Still Steam-Diesel Locomotive. Available online: http://www.douglas-self.com/MUSEUM/LOCOLOCO/kitson/kitsonst.htm (accessed on 6 March 2012).
- Toom, R. Waste heat regeneration systems for internal combustion engines. In Proceedings of Global Powertrain Congress, Berlin, Germany, 18 June 2007.
- Patel, P.S.; Doyle, E.F. Compounding the truck diesel engine with an organic rankine cycle system. In Proceedings of Automotive Engineering Congress and Exposition, Detroit, MI, USA, 23–27 February 1976.
- Oomori, H.; Ogino, S. Waste heat recovery of passenger car using a combination of rankine bottoming cycle and evaporative engine cooling system. SAE Technical Paper 1993. [Google Scholar] [CrossRef]
- Freymann, R.; Strobl, W.; Oblieglo, A. The turbosteamer: A system introducing the principle of cogeneration in automotive applications. MTZ Worldw. 2008, 69, 20–27. [Google Scholar]
- Freymann, R.; Ringler, J.; Seifert, M.; Hörst, T. The second generation turbosteamer. MTZ Worldw. 2012, 73, 18–23. [Google Scholar] [CrossRef]
- Leduc, P.; Smague, P. Rankine system for heat recovery: An interesting way to reduce fuel consumption. Ing. L'automob. 2013, 826, 34–39. [Google Scholar]
- Dyer, L.H. Internal Combustion Engine. U.S. Patent 1,339,176, 5 April 1920. [Google Scholar]
- Birkholtz, U.; Grob, E.; Stohrer, U.; Voss, K.; Gruden, D.O.; Wurster, W. Conversion of waste exhaust heat in automobile using FeSi2 thermoelements. In Proceedings of 7th IEEE International Conference on Thermoelectric Energy Conversion, Arlington, VA, USA, 16–18 March 1988.
- Takanose, E.; Tamakoshi, H. The development of thermolectric generator for passenger car. In Proceedings of 12th IEEE International Conference on Thermoelectrics, Yokohama, Japan, 9–11 November 1993.
- Ikoma, K.; Munekiyo, M.; Furuya, K.; Kobayashi, M.; Izumi, T. Thermoelectric Module and Generator for Gasoline Engin Vehicles. In Proceedings of 17th IEEE International Conference on Thermoelectrics, Nagoya, Japan, 24–28 May 1998.
- Ikoma, K.; Munekiyo, M.; Furuya, K.; Kobayashi, M.; Izumi, T. Thermoelectric generator for gasoline engine vehicles using Bi2Te3 modules. J. Jpn Inst. Met. 1999, 63, 1475–1478. [Google Scholar]
- Bass, J.C.; Elsner, N.B.; Leavitt, F.A. Performance of the 1 kw thermoelectric generator for diesel engines. In Proceedings of 13th International Conference on Thermoelectrics, Kansas City, MO, USA, 30 August–1 September 1995.
- Engines, W.A. Facts about the Wright Turbocompound. Available online: http://www.enginehistory.org/Wright/TC%20Facts.pdf (accessed on 10 March 2014).
- Hetting, C.; Tunberg, A. Le camion Scania—Un routier centenaire. Scania World 2002. Available online: http://toolkitstatic.scania.com/scaniaworld/archive/pdf/ScaniaWorld_fr.pdf (accessed on 14 August 2014). (In French).
- Greszler, A. Diesel Turbo-Compound Technology. In Proceedings of DEER Confrerence, Dearborn, MI, USA, 4–7 August 2008.
- Nicolino, J.-F. Récupération D'énergie par Tubocompound: Applications à la Compétition Automobile et à la Série. In Proceedings of Utilisation rationnelle de l'énergie et environnement, Paris, France, 3 April 2012. (In French)
- TIGERS. Available online: http://www.cpowert.com/Products/TIGERS (accessed on 16 December 2013).
- Romagnoli, A.; Bin-Mamat, A.; Martinez-Botas, R. Design and development of a Low Pressure Turbine (LPT) for Turbocompounding Applications Using RICARDO WAVE. In Proceedings of Ricardo Software User Conference and Workshops, Ludwigsburg, Germany, 9–10 April 2013.
- Vuk, C.T. Turbo compounding: A technology who’s time has come. In Proceedings of DEER Conference, Chicago, IL, USA, 21–25 August 2005.
- Petach, M.; Tward, E.; Backhaus, S. Design of A High Efficiency Power Source (HEPS) Based on Thermoacoustic Technology; NASA: Los Alamos, NM, USA, 2004. [Google Scholar]
- Backhaus, S.; Swift, G.W. A thermoacoustic-Stirling heat engine: Detailed study. J. Acoust. Soc. Am. 2000, 107, 3148–3166. [Google Scholar] [CrossRef] [PubMed]
- Wu, Z.; Man, M.; Luo, E.; Dai, W.; Zhou, Y. Experimental investigation of a 500 W traveling-wave thermoacoustic electricity generator. Chin. Sci. Bull. 2011, 56, 1975–1977. [Google Scholar]
- Struzyna, R.; Span, R.; Eifler, W. Utilization of waste heat through thermodynamic cycles. In Proceedings of 20th Aachen colloquium Automobile and engine technology, Aachen, Germany, 10–12 October 2011.
- Patterson, D.J.; Kruiswyk, R.W. An engine system approach to exhaust waste heat recovery. In Proceedings of DEER Conference, Detroit, MI, USA, 13–16 August 2007.
- Morrison, O.; Seal, M.; West, E.; Connelly, W. Use of a thermophotovoltaic generator in a hybrid electric vehicle. In Proceedings of Thermophotovoltaic Generation of Electricity: Fourth NREL Conference, Denver, CO, USA, 11–14 October 1999.
- Bernhart, W. Trends in ICE-Technologies. In Proceedings of Automotive Megatrends, Dearborn, MI, USA, 19–20 March 2013.
- Baker, H.; Cornwell, R.; Koehler, E.; Patterson, J. Review of low carbon technologies for heavy goods vehicles—Annex 1. Available online: http://www.ukpia.com/Libraries/Download/Review-of-Low-Carbon-Technologies-for-HGVs.sflb.ashx (accessed on 11 August 2014).
- Pattison, N. Automotive world megatrends. In Proceedings of Automotive Megatrends, Brussels, Belgium, 12–13 November 2013.
- Fairbanks, J.W. Automotive thermoelectric generators and HVAC. In Proceedings of DEEE Conference, Dearborn, MI, USA, 16–19 October 2012.
- Seal, M. Quiet, Clean, Multi-Fueled, Multi-Kilowatt Thermophotovoltaic Generator; Western Washington University: Bellingham, WA, USA, 2000. [Google Scholar]
- Hsieh, Y.Y.; Lin, T.F. Evaporation heat transfer and pressure drop of refrigerant R-410A flow in a vertical plate heat exchanger. J. Heat Transf. 2003, 125, 852–857. [Google Scholar] [CrossRef]
- Lemort, V.; Quoilin, S.; Cuevas, C.; Lebrun, J. Testing and modeling a scroll expander integrated into an organic Rankine cycle. Appli. Therm. Eng. 2009, 29, 3094–3102. [Google Scholar]
- Legros, A.; Guillaume, L.; Diny, M.; Zaidi, H.; Lemort, V. Experimental investigations of the valorization of the exhaust waste heat of a gasoline engine based on a rankine cycle. In Presented at FISITA World Automotive Congress, Maastricht, The Netherlands, 3 June 2014.
- Pettersson, F. Simulation of a Turbo Charged Spark Ignited Engine. Master Thesis, Linköpings Universitet, Linköping, Sweden, 2000. [Google Scholar]
- Pacejka, H. Tire and Vehicle Dynamics; Butterworth-Heinemann: Oxford, UK, 2012. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Legros, A.; Guillaume, L.; Diny, M.; Zaïdi, H.; Lemort, V. Comparison and Impact of Waste Heat Recovery Technologies on Passenger Car Fuel Consumption in a Normalized Driving Cycle. Energies 2014, 7, 5273-5290. https://doi.org/10.3390/en7085273
Legros A, Guillaume L, Diny M, Zaïdi H, Lemort V. Comparison and Impact of Waste Heat Recovery Technologies on Passenger Car Fuel Consumption in a Normalized Driving Cycle. Energies. 2014; 7(8):5273-5290. https://doi.org/10.3390/en7085273
Chicago/Turabian StyleLegros, Arnaud, Ludovic Guillaume, Mouad Diny, Hamid Zaïdi, and Vincent Lemort. 2014. "Comparison and Impact of Waste Heat Recovery Technologies on Passenger Car Fuel Consumption in a Normalized Driving Cycle" Energies 7, no. 8: 5273-5290. https://doi.org/10.3390/en7085273
APA StyleLegros, A., Guillaume, L., Diny, M., Zaïdi, H., & Lemort, V. (2014). Comparison and Impact of Waste Heat Recovery Technologies on Passenger Car Fuel Consumption in a Normalized Driving Cycle. Energies, 7(8), 5273-5290. https://doi.org/10.3390/en7085273