Multiagent-Based Distributed Load Shedding for Islanded Microgrids
Abstract
:1. Introduction
2. Multiagent-Based Distributed Load Shedding
2.1. Distributed Information Processing Method
2.2. Local Evaluation of the Comprehensive Weight

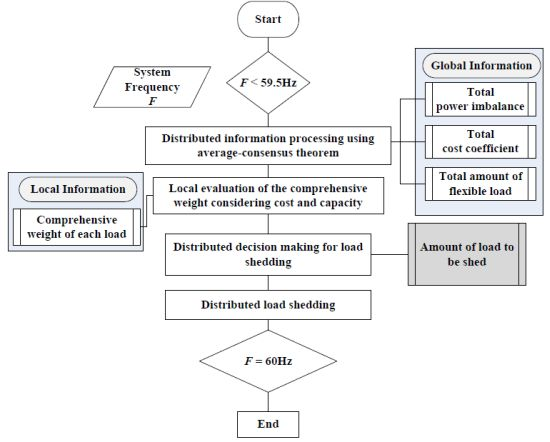
2.3. Flowchart of the Proposed Multiagent-Based Distributed Load Shedding
- Detect power imbalance and collect operation and control data;
- Exchange data with neighbors for distributed information processing;
- Discover the global information including the active total power imbalance PIB as in Equation (13) the total cost coefficient as in Equation (10) and the total amount of flexible loads as in Equation (11);
- Make local evaluation of the cost index as in Equation (10), the capacity index as in Equation (11) and comprehensive weight as in Equation (12).
3. Case Studies

3.1. Case A: Overload
| Load Number | Case A | |||
|---|---|---|---|---|
| χi | CFLi/kW | εi1 | εi2 | |
| 1 | 0.1 | 1 | 0.3 | 0.7 |
| 2 | 0.3 | 2 | 0.3 | 0.7 |
| 3 | 0.4 | 3 | 0.3 | 0.7 |
| 4 | 0.9 | 7 | 0.3 | 0.7 |
| 5 | 0.6 | 5 | 0.3 | 0.7 |
| Load Number | Parameters of loads in Case B | |||
|---|---|---|---|---|
| χi | CFLi/kW | εi1 | εi2 | |
| 1 | 0.1 | 1 | 0.6 | 0.4 |
| 2 | 0.3 | 2 | 0.6 | 0.4 |
| 3 | 0.4 | 3 | 0.6 | 0.4 |
| 4 | 0.9 | 7 | 0.6 | 0.4 |
| 5 | 0.6 | 5 | 0.6 | 0.4 |
| 6 | 0.5 | 4 | 0.6 | 0.4 |


3.2. Case B: New Load Plugs in Operation

4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ahn, C.; Peng, H. Decentralized and real-time power dispatch control for an islanded microgrid supported by distributed power sources. Energies 2013, 6, 6439–6454. [Google Scholar] [CrossRef]
- Peças, L.J.A.; Moreira, C.L.; Madureira, A.G. Defining control strategies for microgrids islanded operation. IEEE Trans. Power Syst. 2006, 2, 916–924. [Google Scholar]
- Lasseter, R.H. Microgrids and distributed generation. J Energy Eng 2007, 3, 144–149. [Google Scholar] [CrossRef]
- Kim, J.Y.; Jeon, J.H.; Kim, S.K.; Cho, C.; Park, J.H.; Kim, H.M.; Nam, K.Y. Cooperative control strategy of energy storage system and microsources for stabilizing the microgrid during islanded operation. IEEE Trans. Power Electron. 2010, 12, 3037–3048. [Google Scholar]
- Giroletti, M.; Farina, M.; Scattolini, R. A hybrid frequency/power based method for industrial load shedding. Int. J. Electr. Power Energy Syst. 2012, 1, 194–200. [Google Scholar] [CrossRef]
- Lukas, S.; Ignacio, E.; Luis, R. A method for the design of UFLS schemes of small isolated power systems. IEEE Trans. Power Syst. 2012, 2, 951–958. [Google Scholar]
- Terzija, V.V. Adaptive underfrequency load shedding based on the magnitude of the disturbance estimation. IEEE Trans. Power Syst. 2006, 3, 1260–1266. [Google Scholar] [CrossRef]
- Seyedi, H.; Sanaye-Pasand, M. New centralized adaptive load-shedding algorithms to mitigate power system blackouts. IET Gen. Transm. Distrib. 2009, 1, 99–114. [Google Scholar] [CrossRef]
- Hamid, B.; Abderrahmane, O.; Nadir, G.; Farid, M.; Nikos, E.M. A new approach applied to adaptive centralized load shedding scheme. In Proceedings of the 8th WSEAS International Coference on Circuits, Systems, Electronics, Control and Signal Processing (CSECS’09), Puerto De La Cruz, Tenerife, Canary Islands, Spain, 14–16 December, 2009; pp. 28–33.
- Otomega, B.; Glavic, M.; Cutsem, T.V. Distributed under voltage load shedding. IEEE Trans. Power Syst. 2007, 4, 2283–2284. [Google Scholar] [CrossRef]
- Kim, H.M.; Kinoshita, T.; Shin, M.C. A multiagent system for autonomous operation of islanded microgrids based on a power market environment. Energies 2010, 3, 1972–1990. [Google Scholar] [CrossRef]
- Xiao, Z.; Li, T.; Huang, M.; Shi, J.; Yang, J.; Yu, J.; Wu, W. Hierarchical MAS based control strategy for microgrid. Energies 2010, 3, 1622–1638. [Google Scholar] [CrossRef]
- Yoo, C.H.; Chung, I.Y.; Lee, H.J.; Hong, S.S. Intelligent control of battery energy storage for multi-agent based microgrid energy management. Energies 2013, 6, 4956–4979. [Google Scholar] [CrossRef]
- Kim, H.M.; Lim, Y.; Kinoshita, T. An intelligent multiagent system for autonomous microgrid operation. Energies 2012, 5, 3347–3362. [Google Scholar] [CrossRef]
- Xu, Y.; Liu, W. Novel multiagent based load restoration algorithm for microgrids. IEEE Trans. Smart Grid 2011, 1, 152–161. [Google Scholar] [CrossRef]
- Lim, Y.; Kim, H.M.; Kinoshita, T. Distributed load-shedding system for agent-based autonomous microgrid operations. Energies 2014, 7, 385–401. [Google Scholar] [CrossRef]
- Fahrioglu, M.; Fernando, L.; Alvarado. Designing incentive compatible contracts for effective demand management. IEEE Trans. Power Syst. 2000, 4, 1255–1260. [Google Scholar]
- Fahrioglu, M.; Alvarado Fernando, L. Using utility information to calibrate customer demand management behavior models. IEEE Trans. Power Syst. 2001, 2, 317–322. [Google Scholar] [CrossRef]
- Lasseter, R.H. Certs Microgrid. In Proceedings of the IEEE International Conference on System of Systems Engineering, San Antonio, TX, USA, 16–18 April 2007.
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Wu, X.; Jiang, P.; Lu, J. Multiagent-Based Distributed Load Shedding for Islanded Microgrids. Energies 2014, 7, 6050-6062. https://doi.org/10.3390/en7096050
Wu X, Jiang P, Lu J. Multiagent-Based Distributed Load Shedding for Islanded Microgrids. Energies. 2014; 7(9):6050-6062. https://doi.org/10.3390/en7096050
Chicago/Turabian StyleWu, Xi, Ping Jiang, and Jing Lu. 2014. "Multiagent-Based Distributed Load Shedding for Islanded Microgrids" Energies 7, no. 9: 6050-6062. https://doi.org/10.3390/en7096050
APA StyleWu, X., Jiang, P., & Lu, J. (2014). Multiagent-Based Distributed Load Shedding for Islanded Microgrids. Energies, 7(9), 6050-6062. https://doi.org/10.3390/en7096050