Fault Current Characteristics of the DFIG under Asymmetrical Fault Conditions
Abstract
:1. Introduction
2. Doubly-Fed Induction Generator (DFIG) Equations in Space Vector Notation

3. Dynamic Behavior of the Rotor Current
3.1. Modeling of the Rotor-Side Converter (RSC)

3.2. Range of the Crossover Frequency and Phase Margin
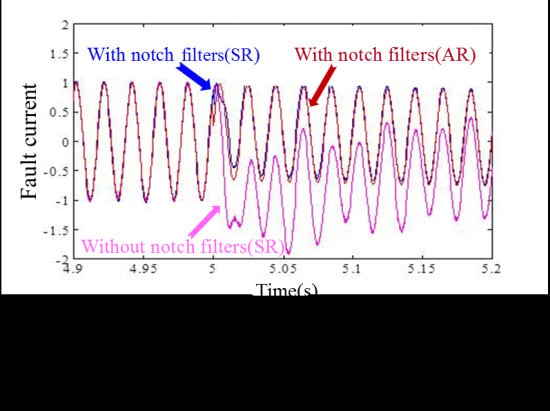
3.3. Transient Characteristics of Rotor-Side Converter (RSC)


4. Dynamic Performance of Stator Flux Linkage
5. Fault Current Characteristics of the Doubly-Fed Induction Generator (DFIG)
6. Simulation Study
6.1. Heading Steady-state Reference Signals of Rotor Current
6.2. Simulation Analysis

6.2.1. Stator Flux Linkage

6.2.2. Rotor Current and Stator Current




7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
Appendix B
References
- Muller, S.; Deicke, M.; de Doncker, R.W. Doubly fed induction generator systems for wind turbines. IEEE Ind. Appl. Mag. 2002, 8, 26–33. [Google Scholar] [CrossRef]
- Iwanski, G.; Koczara, W. DFIG-based power generation system with UPS function for variable-speed applications. IEEE Trans. Ind. Electron. 2008, 55, 3047–3054. [Google Scholar] [CrossRef]
- Jauch, C.; Matevosyan, J.; Ackermann, T.; Bolik, S. International comparison of requirements for connection of wind turbines to power systems. Wind Energy 2005, 8, 295–306. [Google Scholar] [CrossRef]
- The grid Code 3. Available online: http//www.nationalgrid.com/uk/Electricity/Codes/gridcode (accessed on 1 January 2006).
- Transmission Code 2007—Network and System Rules of the German Transmission System Operators. Available online: https://www.bdew.de/ (accessed on 1 August 2007).
- Technical Rule for Connecting Wind Farm to Power System; Technical Report for Inspection and Quarantine of the People’s Republic of China: Beijing, China, 2011.
- Howard, D.F.; Habetler, T.G.; Harley, R.G. Improved sequence network model of wind turbine generators for short-circuit studies. IEEE Trans. Energy Convers. 2012, 27, 968–977. [Google Scholar] [CrossRef]
- Morren, J.; de Haan, S.W.H. Ridethrough of wind turbines with doubly-fed induction generator during a voltage dip. IEEE Trans. Energy Convers. 2005, 20, 435–441. [Google Scholar] [CrossRef]
- Lopez, J.; Sanchis, P.; Roboam, X.; Marroyo, L. Dynamic behavior of the doubly-fed induction generator during three-phase voltage dips. IEEE Trans. Energy Convers. 2007, 22, 709–717. [Google Scholar] [CrossRef]
- Morren, J.; de Haan, S.W. Short-circuit current of wind turbines with doubly fed induction generator. IEEE Trans. Energy Convers. 2007, 22, 174–180. [Google Scholar] [CrossRef]
- Pannell, G.; Atkinson, D.J.; Zahawi, B. Analytical study of grid-fault response of wind turbine doubly fed induction generator. IEEE Trans. Energy Convers. 2010, 25, 1081–1091. [Google Scholar] [CrossRef]
- Zhang, L.H.; Cai, X.; Guo, J.H. Dynamic response of DFIG fault currents under constant AC exitation condition. In Proceedings of the 2009 Asia-Pacific Power Energy Engineering Conference (APPEEC), Wuhan, China, 27–31 March 2009; pp. 1–4.
- Wu, Z.R.; Wang, G.; Li, H.F.; Gao, X. Equivalent Model for Calculating Short Circuit Current of Doubly Fed Wind Generator under Uninterrupted Excitation. In Proceedings of the 2011 Power Energy Engineering Conference (APPEEC), Wuhan, China, 25–28 March 2011; pp. 1–4.
- Kong, X.; Zhang, Z.; Yin, X. Study of Fault Current Characteristics of the DFIG Considering Dynamic Response of the RSC. IEEE Trans. Energy Convers. 2014, 29, 278–287. [Google Scholar]
- Ouyang, J.; Xiong, X. Dynamic behavior of the excitation circuit of a doubly-fed induction generator under a symmetrical voltage drop. Renew. Energy 2014, 71, 629–638. [Google Scholar] [CrossRef]
- Timbus, V.; Ciobotaru, M.; Teodorescu, R.; Blaabjerg, F. Adaptive Resonant Controller for Grid-Connected Converters in Distributed Power Genaration Systems. In Proceedings of the Twenty-First Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Dallas, TX, USA, 26–30 March 2006; pp. 1601–1606.
- Nian, H.; Song, Y.; Zhou, P.; He, Y. Improved direct power control of a wind turbine driven doubly fed induction generator during transient grid voltage unbalance. IEEE Trans. Energy Convers. 2011, 26, 976–986. [Google Scholar] [CrossRef]
- Yazdani, D.; Bakhshai, A.; Joos, G. A Real-Time Sequence Components Decomposition for Transient Analysis in Grid-Connected Distributed Generation Systems. In Proceedings of the IEEE International Symposium on Industrial Electronics (ISIE), Cambridge, UK, 30 June–2 July 2008; pp. 1651–1656.
- Leonhard, W. Control of Electrical Drives; Springer-Verlag: Berlin, Germany, 1995. [Google Scholar]
- Marques, G.D.; Sousa, D.M. Understanding the doubly fed induction generator during voltage dips. IEEE Trans. Energy Convers. 2012, 27, 421–461. [Google Scholar] [CrossRef]
- Hopfensperger, B.; Atkinson, D.J. Stator-flux-oriented control of a doubly-fed induction machine with and without position encoder. IEE Proc. Electr. Power Appl. 2000, 147, 241–250. [Google Scholar] [CrossRef]
- Wang, L.; Zhu, H.; Yang, Z. Tuning Method for PI Controllers of PMSM Driving System. Trans. China Electrotech. Soc. 2014, 5, 104–117. [Google Scholar]
- Lopez, J.; Gubia, E.; Olea, E.; Ruiz, J.; Marroyo, L. Ride through of wind turbines with doubly fed induction generator under symmetrical voltage dips. IEEE Trans. Ind. Electron. 2009, 56, 4246–4254. [Google Scholar] [CrossRef]
- Liu, Q.H.; He, Y.K.; Zhang, J.H. Operation control and modeling simulation of AC-excited variable-speed constant-frequency wind power generator. Proc. CSEE 2006, 26, 43–50. [Google Scholar]
- Jia, J.C.; Liu, J.; Zhang, Y.G. Dynamic characteristics of stator flux of doubly-fed induction generator during grid voltage fault. Proc. CSEE 2011, 31, 90–96. [Google Scholar]
- Lie, X.; Yi, W. Dynamic modeling and control of DFIG based wind turbines under unbalanced network conditions. IEEE Trans. Power Syst. 2007, 22, 314–323. [Google Scholar]
- Hu, J. Investigation on the Ride-Through Operation of DFIG-based Wind Power Generation Systems during Grid Fault-Basic Theory and Key Technology. Ph.D. Thesis, Zhejiang University, Hangzhou, China, 2009. [Google Scholar]
- Zheng, Z.; Yang, G.; Geng, H. Coordinated control of a doubly-fed induction generator-based wind farm and a static synchronous compensator for low voltage ride-through grid code compliance during asymmetrical grid faults. Energies 2013, 6, 4660–4681. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, Q.; Xu, H.; Guo, Q.; Sun, H. Fast coordinated control of DIFG wind turbine generators for low and high voltage ride-through. Energies 2014, 7, 4140–4156. [Google Scholar] [CrossRef] [Green Version]
- Wu, Z.; Zhu, C.; Hu, M. Improved control strategy for DIFG wind turbines for low voltage ride through. Energies 2013, 6, 1181–1197. [Google Scholar] [CrossRef]
- Yao, J.; Li, H.; Liao, Y.; Chen, Z. An improved control strategy of limiting the dc-link voltage fluctuation for a doubly fed induction wind generator. IEEE Trans. Power Electron. 2008, 23, 1205–1213. [Google Scholar]
- Papadimitriou, C.N.; Vovos, N.A. Transient response improvement of microgrids exploiting the inertia of a Doubly-Fed Induction Generator (DFIG). Energies 2010, 3, 1049–1066. [Google Scholar] [CrossRef]
- Arribas, J.R.; Rodríguez, A.F.; Muñoz, Á.H.; Nicolás, C.V. Low voltage ride-through in DFIG wind generators by controlling the rotor current without crowbars. Energies 2014, 7, 498–519. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, F.; Zhang, Z.; Yin, X. Fault Current Characteristics of the DFIG under Asymmetrical Fault Conditions. Energies 2015, 8, 10971-10992. https://doi.org/10.3390/en81010971
Xiao F, Zhang Z, Yin X. Fault Current Characteristics of the DFIG under Asymmetrical Fault Conditions. Energies. 2015; 8(10):10971-10992. https://doi.org/10.3390/en81010971
Chicago/Turabian StyleXiao, Fan, Zhe Zhang, and Xianggen Yin. 2015. "Fault Current Characteristics of the DFIG under Asymmetrical Fault Conditions" Energies 8, no. 10: 10971-10992. https://doi.org/10.3390/en81010971
APA StyleXiao, F., Zhang, Z., & Yin, X. (2015). Fault Current Characteristics of the DFIG under Asymmetrical Fault Conditions. Energies, 8(10), 10971-10992. https://doi.org/10.3390/en81010971