Comparison of Wind Energy Generation Using the Maximum Entropy Principle and the Weibull Distribution Function

Abstract

Proper knowledge of the wind characteristics of a site is of fundamental importance in estimating wind energy output from a selected wind turbine. The present paper focuses on assessing the suitability and accuracy of the fitted distribution function to the measured wind speed data for Baburband site in Sindh Pakistan. Comparison is made between the wind power densities obtained using the fitted functions based on Maximum Entropy Principle (MEP) and Weibull distribution. In case of MEP-based function a system of (N+1) non-linear equations containing (N+1) Lagrange multipliers is defined as probability density function. The maximum entropy probability density functions is calculated for 3–9 low order moments obtained from measured wind speed data. The annual actual wind power density (P_A) is found to be 309.25 W/m² while the Weibull based wind power density (P_W) is 297.25 W/m². The MEP-based density for orders 5, 7, 8 and 9 (P_E) is 309.21 W/m², whereas for order 6 it is 309.43 W/m². To validate the MEP-based function, the results are compared with the Weibull function and the measured data. Kolmogorov–Smirnov test is performed between the cdf of the measured wind data and the fitted distribution function (Q₉₅ = 0.01457 > Q = 10⁻⁴). The test confirms the suitability of MEP-based function for modeling measured wind speed data and for the estimation of wind energy output from a wind turbine. R² test is also performed giving analogous behavior of the fitted MEP-based pdf to the actual wind speed data (R² ~ 0.9). The annual energy extracted using the chosen wind turbine based on Weibull function is P_W = 2.54 GWh and that obtained using MEP-based function is P_E = 2.57–2.67 GWh depending on the order of moments.

1. Introduction

The exponentially growing needs of energy and degradation of environmental conditions are some of the important factors behind the promotion of renewable and clean sources of energy into the energy mix on national and localized power grids. These renewable sources of energy include wind, solar photovoltaic, solar thermal, geothermal, biomass, and tidal to name the main ones. Of these sources, the wind energy has been commercially developed, accepted, and available for small to very large grid connected applications. The cumulative global wind power installed capacity reached 432,419 MW at the end of 2015 compared to 17,400 MW in year 2000, an increase of about 2485.2% in 16 years period. Compared to 2014 the cumulative installed capacity increased by 17% from 369,695 MW in 2014 to 432,419 MW in 2015 [1]. It has been established that power of the wind is worth deploying in all parts of the world and Pakistan in particular. For successful and profitable development, the understanding of wind speed variation and its availability for power production is critical. Wind is highly fluctuating meteorological parameters with time and location and hence need to be understood well. The present study aims at analyzing the wind speed data using Maximum Entropy Principle (MEP) and compares it with Weibull distribution function for wind power production at a selected site.

MEP is a widely used technique in various applications ranging from statistical and quantum mechanics to decision theory financial modelling. The MEP concept was presented by Jaynes [2,3] such that for any given available information about the distribution, an approach is established for finding the least informative probability distribution. MEP is based on a procedure that provides a link between Shannon’s information theory [4] and statistical mechanics. The underlying approach is to construct a probability distribution that agrees with the given distribution having a particular set of quantities of the system background investigation. The procedure is based on the idea that among all the infinite number of distributions compatible with data distribution, a distribution which maintains the largest degree of uncertainty is the one which must be selected. In order to express uncertainty in a distribution, Shannon’s entropy [4] is used. Shannon’s entropy as a measure of uncertainty is maximized to obtain the probability distribution function. As an example of this principle, maximum entropy probability distribution function for a random variable (wind speed) is determined by setting up first few low order moments as constraints on the given data distribution.

The Maximum Entropy Principle and Minimum Cross Entropy [2,3,4,5,6,7] are used to calculate distribution function. Liu and Chang [8] used probability density function with the maximum entropy and stated that wind regimes have two humps. The maximum entropy distributions outperformed the Weibull function, irrespective of wind speed or power density analyzed. Wu [9] calculated maximum entropy densities for employee income distributions and compared it with the conventional income distributions. In renewable wind energy sector, Li et al. [10,11] used MEP to estimate wind energy potential as an alternative to the Weibull distribution function and proposed a theoretical method of calculating the probability density function for wind speed data distribution. These studies utilized the idea of conservation of wind’s mass that is mass of wind molecules in motion, momentum, and energy to construct family of distributions derived from maximum entropy principle by employing a pre-exponential term. The above studies formulated distribution functions for diurnal, monthly, seasonal and yearly wind speed variations.

Rehman et al. [12] used Weibull distribution to represent the wind speed data and found an excellent fit between the measured values and the two parameters based model. Bagiorgas et al. [13] conducted wind power potential assessment for seven locations in the Aegean Sea (Greece) using the Weibull distribution and obtained close agreement between the measured and modeled values. In another study Bagiorgas et al. [14] four different methods to model the measured wind speed data and estimated most energy carrying wind speed were compared. Sulaiman et al. [15] examined the measured wind speed data in Oman using the Weibull function and the Kolmogorove Smirnov test and reported the goodness of fit considering 1% and 5% of confidence level. Rehman et al. [16] studied the wind characteristics using two parameter Weibull distributions.

Ramírez and Carta [17] investigated the hourly wind speed data recorded at weather stations located in the Canarian Archipelago and constructed a probability distribution function based on maximum entropy principle (MEP). The study concluded that a MEP-based function constrained by three low order moments presents a lower relative error in estimation of wind power density as compared to the power density estimated using the Weibull distribution function. Zhou et al. [18] presented a comprehensive analysis of wind speed from five sites in North Dakota (USA) using MEP. The study in addition to MEP-based distribution also included Weibull, Rayleigh, Gamma, Lognormal, inverse Gaussian distributions. The study concluded that MEP-based distribution is more flexible as compared to other distribution functions. Zhang et al. [19] investigated the wind speed data recorded using intertidal anemometer tower located at Rudong in the East China Sea. The recorded wind speed data was fitted to the Weibull function and a probability function using MEP. The study revealed that probability density function based on MEP performed well in fitting the wind speed data.

The present study is devoted to the determination of monthly and yearly maximum entropy probability density function for Baburband, Sindh Pakistan. A comparison with the conventional empirical Weibull distribution function is also made and the suitability of the MEP-based function is discussed for the investigated site.

2. Materials and Methods

The present study utilized wind speed data measured at 80 m above ground level over a period of one year at a wind resource assessment site at Baburband in Pakistan during 2010. The study modeled the measured wind speed data using Weibull and MEP-based functions to estimate the wind power density and the energy yield using a wind turbine of 1000 kW rated power. The obtained modeled results are evaluated using different statistical tests. The mathematical procedure and equations used in this paper are provided in Section 2.1, Section 2.2, Section 2.3, Section 2.4, Section 2.5, Section 2.6 and Section 2.7.

2.1. Maximum Entropy Method

The method is based on the determination of a continuous function of a random variable f(v) by iteratively maximizing the entropy subject to first few low order moment constraints obtained from the given wind speed data. The function so obtained is known as maximum entropy probability (MEP) density function which models the given wind speed data. The Shannon’s entropy of the probability density function f(v) is given by the following integral equation:

$$H=-{\displaystyle \underset{a}{\overset{b}{\int }}f(v)\ln f(v)dv}$$

(1)

Subject to the given constraints, Shannon’s entropy given in Equation (1) is maximized as follows:

$${\displaystyle \underset{a}{\overset{b}{\int }}f(v)dv=1}$$

(2)

and:

$$E\left\{{\psi }_n(v)\right\}={\displaystyle \underset{a}{\overset{b}{\int }}{\psi }_n(v)f(v)dv}={\mu }_n\hspace{1em}n=0,\mathrm{...},N$$

(3)

where N is the number of constraints imposed on the physical system, μ_n are the N moments constraints obtained from the given data, with μ₀ = 1, ψ₀(v) = 1. ψ_n(v), n = 0, ...., N, are N known functions. Jaynes [2,3] argued that most likely probability density function f(v) is one which maximizes Shannon’s Entropy, subject to given constraints. Using Lagrange’s method the most likely distribution function in the presence of constraints which solves the problem is given by:

$$f(v)=\exp \left[-{\displaystyle \sum _{n=0}^N{\lambda }_n{\psi }_n(v)}\right]$$

(4)

where λ_n (=λ₀, ...., λ_N) are (N + 1) Lagrange multipliers and are determined by solving (N + 1) non-linear equations, given as:

$$L_n(\lambda )={\displaystyle \int {\psi }_n(v)\exp \left[-{\displaystyle \sum _{n=0}^N{\lambda }_n{\psi }_n(v)}\right]dv={\mu }_n\hspace{1em}n=0,\mathrm{...},N}$$

(5)

The distribution function given by Equation (4) is a set of known function having an appropriate value of N and ψ_n(v), n = 0, .... N. ψ_n(v) is taken as some function of power of v or a function of logarithm of v, see refs. [20,21,22,23]. In the present study it is taken as ψ_n(v) = vⁿ.

In order to determine Lagrange multipliers given in Equation (4), (N + 1) non-linear equations given in Equation (5) are solved. The Newton method is used to solve these equation which consists of expanding L_n(v) in terms of Taylor’s series around initial guess values of Lagrange multiplier (λ°). The higher order terms of Taylor’s series are neglected and the resulting equation is iteratively solved to obtain Lagrange multipliers. Using these Lagrange multipliers the probability density function, f(v), is obtained for the given wind speed data. The Taylor’s series expansion of L_n(v) with initial guess values and neglecting higher order terms, the resulting linear equation is given as:

$$L_n(\lambda )\cong L_n({\lambda }^0)+{(\lambda -{\lambda }^0)}^t{\left[\nabla L_n(\lambda )\right]}_{\lambda ={\lambda }^0}={\mu }_n\hspace{1em}n=0,\mathrm{....},N$$

(6)

Let the vectors δ and g are defined as follows:

$$\delta =\lambda -{\lambda }^0$$

(7)

and:

$$g={[{\mu }_0-L_0({\lambda }^0),\mathrm{.......},{\mu }_N-L_N({\lambda }^0)]}^t$$

(8)

The matrix L is given as follows:

$$L=\left[l_{nk}\right]={\left[\frac{\partial L_n(\lambda )}{\partial {\lambda }_k}\right]}_{\lambda ={\lambda }^0}\hspace{1em}n,k=0,\mathrm{....}N$$

(9)

Equation (6) becomes:

$$L\delta =g$$

(10)

The system given in Equation (10) is solved for δ and new value of Langrage multiplier, λ, is obtained as $\lambda ={\lambda }^0+\delta$. Matrix L is symmetric and is given as follows:

$$l_{nk}=l_{kn}=-{\displaystyle \int {\psi }_n(v){\psi }_k(v)\exp \left[-{\displaystyle \sum _{n=0}^N{\lambda }_n{\psi }_n(v)}\right]}dv\hspace{1em}n,k=0,\mathrm{....},N$$

(11)

Equation (11) is iteratively solved and in each iteration N (N − 1)/2 integrals of the form given in Equation (11) are solved. The iterations are continued until δ becomes negligible.

2.2. Weibull Distribution Function and Goodness-of-Fit Tests

In this paper a comparison is made between the theoretically calculated maximum entropy probability density function and the estimated probability density function using the Weibull distribution function [24,25,26,27]. The goodness-of-fit tests for the maximum entropy cumulative distribution function with the cumulative distribution of the measured wind speed data are also performed. The test is performed using R², RMSE and Kolmogorov–Smirnov tests [24]. R² test is performed using the following expression:

$$R^2=\frac{{\displaystyle \sum _{i=1}^n{\left(y_i-z_m\right)}^2-{\displaystyle \sum _{i=1}^n{\left(y_{ic}-y_i\right)}^2}}}{{\displaystyle \sum _{i=1}^n{\left(y_i-z_m\right)}^2}}$$

(12)

and RMSE test is given by:

$$RMSE={\left[\frac{1}{n}{\displaystyle \sum _{i=1}^n{\left(y_i-y_{ic}\right)}^2}\right]}^{1/2}$$

(13)

Kolmogorov–Smirnov test is based on the comparison between cdf of the assumed theoretical function fitted to the actual data and empirical function of the actual data distribution. The logic of the test is as follows: if the maximum vertical deviation of cdf of the assumed function and of empirical function is small, then the assumed cdf is correct. The Kolmogorov-Smirnov test statistics Q is obtained using the following equation:

Q = max[F(v) − G(v)]

(14)

where F(v) is the cumulative distribution function of the assumed theoretical/statistical function and G(v) is a cumulative distribution function evaluated by using either observed or generated wind speed data. The critical value Kolmogorov–Smirnov test for identical sample sizes at 95% confidence level is determined by;

$$Q_{95}=\frac{1.36}{\sqrt{n}}$$

(15)

where n is the total number of data points. If the Q value is greater than the critical value, Q₉₅, this implies that there is a disagreement between the assumed function and the recorded time series data under a given confidence level.

2.3. Wind Power Density Based on Weibull Function and MEP

The wind power density (P_F) for the investigated site is obtained using the given probability density function f(v) as a fit function given in Equation (4) for MEP-based function or for Weibull function [24,25,26,27] using the following integral formula:

$$P_F=\frac{1}{2}{\displaystyle \int {\rho }_a{v}^{3}f(v)dv}$$

(16)

where the probability distribution function f(v) is the Weibull function or MEP-based function, v is the wind speed and ${\rho }_a$ is the air density. Accordingly, Weibull and MEP-based wind power densities are denoted by P_W and P_E, respectively. Furthermore, multiplying Equation (16) by time duration gives wind energy density based on fitted distribution function as E_W for Weibull and E_E for MEP-based function.

A wind turbine converts the mechanical energy of motion of air molecules into electrical energy. In an ideal wind turbine, the generated power increases with increasing wind speed from wind turbine cut-in-speed (v_cin) to rated (v_r) value. At wind speed above rated value till cut-off (v_co), the generated power remains constant and is known as rated power (P_r). Rated power is determined using the following equation;

$$P_r=\frac{1}{2}{\rho }_a\hspace{0.17em}A\hspace{0.17em}{v}_r^3$$

(17)

where A is the intercept area of the rotor of an ideal wind turbine. The turbine stops working at wind speeds above cut-off value of the turbine. Therefore, the total wind energy extracted (E_TI) by a wind turbine is given by;

$$E_{TI}=T{\displaystyle \underset{0}{\overset{\infty }{\int }}P(v)f(v)dv}$$

(18)

$$E_{TI}=T\left({\displaystyle \underset{V_{cin}}{\overset{V_r}{\int }}P(v)f(v)dv}+{\displaystyle \underset{V_r}{\overset{V_{co}}{\int }}{P}_{r}f(v)dv}\right)$$

(19)

P(v) is given by:

$$P(v)=\frac{1}{2}{\rho }_a\hspace{0.17em}A\hspace{0.17em}{v}^3$$

(20)

where T is the time duration for which the wind energy is extracted (e.g., T is 8760 h over the year), P(v) is the power of the wind flowing at a speed v through the blades of a turbine having a swept area A and P_r is the constant rated power produced by an ideal wind turbine, (see Equation (17)). Substituting for P_r and P(v) from Equations (17) and (20), Equation (19) becomes:

$$E_{TI}=\frac{1}{2}{\rho }_{a}AT\left({\displaystyle \underset{v_{cin}}{\overset{v_r}{\int }}{v}^{3}f(v)dv}+v_r^3{\displaystyle \underset{v_r}{\overset{v_{co}}{\int }}f(v)dv}\right)$$

(21)

where f(v) is the distribution function for wind speeds. Using Weibull function in Equation (21), gives:

$$E_{WTI}=\frac{1}{2}{\rho }_{a}AT\left({\displaystyle \underset{v_{cin}}{\overset{v_r}{\int }}{v}^3\frac{k}{c}{\left(\frac{v}{c}\right)}^{k-1}\exp \left(-{\left(\frac{v}{c}\right)}^k\right)dv}+v_r^3{\displaystyle \underset{v_r}{\overset{v_{co}}{\int }}\frac{k}{c}{\left(\frac{v}{c}\right)}^{k-1}\exp \left(-{\left(\frac{v}{c}\right)}^k\right)dv}\right)$$

(22)

and using MEP based distribution function from Equation (4) in Equation (21) gives:

$$E_{ETI}=\frac{1}{2}{\rho }_{a}AT\left({\displaystyle \underset{v_{cin}}{\overset{v_r}{\int }}{v}^3\exp \left(-{\displaystyle \sum _{n=0}^N{\lambda }_n{\psi }_n(v)}\right)dv}+v_r^3{\displaystyle \underset{v_r}{\overset{v_{co}}{\int }}\exp \left(-{\displaystyle \sum _{n=0}^N{\lambda }_n{\psi }_n(v)}\right)dv}\right)$$

(23)

The integrals in Equations (22) and (23) are complex and cannot be solved using analytical techniques. Therefore numerical methods are used to solve these integrals using a 64 point Gauss-Legendre procedure iteratively.

2.4. Wind Energy Extracted by a Wind Turbine

The wind stream interacts with the rotor blades of a wind turbine and the energy contained is converted into the rotational energy of the turbine rotor. Such a wind interaction leads to a reduction in wind speed. The power produced by a wind turbine increases for wind speeds lying between cut-in and rated values of the turbine whereas for wind speeds lying between rated and cut-off values of the turbine, the power output is 100% at maximum efficiency. The actual power (P_AT) generated depends on the performance curve of a turbine and is expressed by the following equation:

$$P_{AT}=\{\begin{array}{ll}0& v<v_{cin}\\ P_C{P}_r& v_{cin}\le v<v_r\\ P_r& v_r\le v<v_{co}\\ 0& v\ge v_{co}\end{array}$$

(24)

where P_C is the selected mathematical function fitted to the performance curve of a wind turbine. A sigmoid function is used to fit the performance curve of the selected wind turbine. The Boltzmann-Sigmoid function is given by:

$$P_C=\frac{A_1-A_2}{1+e^{(x-x_0)/dx}}+A_2$$

(25)

where A₁ and A₂ are initial and final values, x₀ is the point of inflection and dx is the width, determined using the wind turbine power curve data.

The Weibull function is a theoretical distribution function, discussed elsewhere [13], as the function of a continuous variable and here it is taken as a function of wind speed v, denoted by f(v). Whereas f(v) is taken as MEP-based function in Equation (4). The actual wind energy output (E_TA) from the selected wind turbine can be determined using Weibull or MEP-based function in conjunction with Equations (19), (20) and (24). The actual wind energy output, is obtained by multiplying P_AT(v) with the probability distribution of wind speeds f(v) and by integrating over the possible wind speed range lying in the domain of the wind turbine performance curve:

$$E_{TA}=T{\displaystyle \underset{v_{cin}}{\overset{v_{co}}{\int }}{P}_{AT}(v)f(v)dv}=T{P}_r{\displaystyle \underset{v_{cin}}{\overset{v_r}{\int }}{P}_{C}f(v)dv}+T{P}_r{\displaystyle \underset{v_r}{\overset{v_{co}}{\int }}f(v)dv}$$

(26)

In case of Weibull function Equation (26) becomes:

$$E_{WTA}=T{P}_r{\displaystyle \underset{v_{cin}}{\overset{v_r}{\int }}{P}_C\frac{k}{c}{\left(\frac{v}{c}\right)}^{k-1}\exp \left(-{\left(\frac{v}{c}\right)}^k\right)dv}+T{P}_r{\displaystyle \underset{v_r}{\overset{v_{co}}{\int }}\frac{k}{c}{\left(\frac{v}{c}\right)}^{k-1}\exp \left(-{\left(\frac{v}{c}\right)}^k\right)dv}$$

(27)

and in case of MEP based function Equation (26) becomes:

$$E_{ETA}=T{P}_r{\displaystyle \underset{v_{cin}}{\overset{v_r}{\int }}{P}_C\exp \left(-{\displaystyle \sum _{n=0}^N{\lambda }_n{\psi }_n(v)}\right)dv}+T{P}_r{\displaystyle \underset{v_r}{\overset{v_{co}}{\int }}\exp \left(-{\displaystyle \sum _{n=0}^N{\lambda }_n{\psi }_n(v)}\right)dv}$$

(28)

The integrals appearing in Equations (27) and (28) are complex and are determined numerically by a 64 point Gauss-Legendre procedure.

2.5. Wind Turbine Efficiency, ε

The efficiency of a turbine, ε, is evaluated by taking a ratio between the total wind energy extracted from a turbine and energy generated by an ideal wind turbine. Mathematically, this is expressed as follows:

$$\epsilon =\frac{E_{TA}}{E_{TI}}$$

(29)

Equations (22), (23) and (27)–(29) suggest that the efficiency of a turbine is not only a function of the performance curve of a turbine but is also depends on the wind speed data. In 1926, Betz [28] discovered a law which puts a limit on the maximum amount of energy that can be extracted from wind. Assuming transmission losses are negligible, the maximum power extracted from wind should not exceed 59% of the available power in the wind.

2.6. Capacity Factor, C_F

The productivity of a wind turbine can also be assessed by a turbine characteristic known as capacity factor. It is evaluated by taking a ratio of the total power produced by a wind turbine in specific time duration to the generated power of the turbine when operating at full 100% output for the same duration of time. Operating at 100% output power of a turbine during the time duration T, the rated wind energy is given by:

$$E_{Tr}=T{P}_r$$

(30)

Capacity factor is obtained by dividing the actual wind energy produced using Equation (26) by rated wind energy as follows:

$$C_F=\frac{E_{TA}}{E_{Tr}}={\displaystyle \underset{v_{cin}}{\overset{v_r}{\int }}{P}_{C}f(v)dv+{\displaystyle \underset{v_r}{\overset{v_{co}}{\int }}f(v)dv}}$$

(31)

where P_C and f(v) are power curve function and probability distribution functions, respectively.

2.7. Availability Factor, A_F

The availability factor, A_F, measures the percentage of time the turbine remains operational, which in turn depends on the turbine and wind characteristics. The availability factor A_F is the probability that wind speed lies between cut-in and cut-off wind speed values of the turbine, P(v_cin ≤ v < v_co) and is determined by the following integral:

$$A_F={\displaystyle \underset{v_{cin}}{\overset{v_{co}}{\int }}f(v)dv}$$

(32)

As the cut-in wind speed decreases and cut-off and mean wind speed increase, the availability factor increases. A turbine having a high availability factor value implies that for most of the time, the turbine is working partially, i.e., is working at less than its full capacity. Therefore in addition to the wind speed availability, the productivity of the turbine also dependents on capacity factor and turbine efficiency.

3. Results and Discussion

Wind speed data for Baburband was acquired from AEDB Government of Pakistan [29]. The site and wind speed data specifications are given in

Table 1. Site and wind speed data specification.

Location	Characteristic	Value
Baburband	Latitude	25°07′36.08″N
	Longitude	67°38′06.89″N
	Mast Height	80 m
	Recording Time Interval	10 min averaged
	# of wind speed data points	51,000

.

The analysis is performed on time-series wind speed data collected in 10 min time interval for a period of one year (2010). The wind speed data was recorded using three-cup shaped anemometer in the range 0 to 30 m/s with a threshold of 0.00345 m/s and has a resolution of 0.056 m/s. The Baburband site is located northeast of Karachi, Pakistan on the Super Highway. Monthly and yearly descriptive statistics of the measured data are given in

Table 2. Monthly and yearly descriptive statistics of the recorded wind speed data for Baburband wind masts, at 80 m height for the year 2010.

Month	Data Points	Mean Vavg (m/s)	Range (m/s)	σ (m/s)	K	S	PA (W/m2)	CV %	C.I. (95.0%)
January	744	5.52	12.08	2.45	−0.75	0.18	165.33	44.42	0.18
February	672	5.53	11.62	2.61	−0.59	0.43	177.25	47.23	0.20
March	744	5.82	12.38	2.40	−0.33	0.43	185.61	41.23	0.17
April	720	7.51	13.05	2.79	−0.72	0.04	366.95	37.23	0.20
May	744	9.59	15.80	3.12	−0.06	0.43	719.91	32.56	0.22
June	720	9.53	14.18	2.58	−0.34	0.05	647.84	27.07	0.19
July	744	7.73	17.17	3.28	0.32	0.70	451.21	42.44	0.24
August	696	6.84	13.56	3.04	−0.66	0.24	316.56	44.51	0.23
September	720	5.98	10.20	2.07	−0.58	−0.04	177.42	34.65	0.15
October	744	4.95	8.80	1.79	−0.66	0.11	104.01	36.19	0.13
November	719	5.61	12.94	2.66	−0.67	0.41	185.45	47.39	0.19
December	744	5.98	12.68	2.59	−0.74	0.10	205.57	43.43	0.19
Yearly	8711	6.72	18.20	3.04	0.10	0.53	309.25	45.29	0.06

. The monthly mean wind speed varied between a minimum of 4.95 m/s in October to a maximum of 9.59 m/s in May with an increasing trend from January to May and then a decreasing trend towards the end of the year see column 3 of Table 2. At 80 m height, the overall average wind speed of 6.72 m/s was observed with standard deviation of 3.04 m/s, confidence interval (C.I.) of 0.06 and a confidence level (C.L.) of 95.0% (see Table 2). The wind power density at 80 m varied between 104.01 W/m² and 719.91 W/m² corresponding to October and May, as observed from the data shown in column 8 of Table 2. Wind power density followed almost the same trend like monthly mean wind speed over the year. However, the coefficient of variations (CV) of 45.29% is observed for the total number of data points. This implies that 55% of wind speed data points fall in a C.I. window of 0.06 around mean wind speed in the whole 12 months period on the average. Furthermore, the measured wind speed distribution is positively skewed (S = 0.53). This implies that larger number of wind speed data points is located to the right of the mean wind speed.

Using hourly averaged wind speed data, monthly and overall Weibull and Maximum Entropy probability and cumulative functions (pdf and cdf) are determined. The Weibull shape and scale parameters are estimated using Modified Maximum Likelihood Method (MMLM) and are summarized in

Table 3. Monthly and Yearly Wind Characteristics for Baburband at 80 m height using modified maximum likelihood method (MMLM) for 2010.

Month	Hours	k	C (m/s)	Vm (m/s)	Vmp (m/s)	PW (W/m2)	R2	RMSE	χ2
January	742	2.40	6.16	5.41	4.92	160.71	0.99	2.95 × 10−3	8.73 × 10−6
February	670	2.32	6.43	5.64	5.05	187.51	0.99	3.23 × 10−3	1.05 × 10−5
March	742	2.37	6.16	5.40	4.89	161.69	0.99	2.59 × 10−3	6.71 × 10−6
April	718	2.88	8.30	7.33	7.16	353.66	0.99	3.01 × 10−3	9.06 × 10−6
May	742	3.04	10.17	8.99	8.91	634.96	0.99	1.61 × 10−3	2.59 × 10−6
June	718	4.17	10.70	9.63	10.02	678.78	0.99	2.83 × 10−3	8.02 × 10−6
July	742	2.45	8.62	7.57	6.96	433.45	0.99	1.94 × 10−3	3.77 × 10−6
August	694	2.24	7.34	6.44	5.64	286.19	0.99	3.40 × 10−3	1.15 × 10−5
September	718	3.01	6.29	5.57	5.51	150.98	0.99	1.65 × 10−3	2.72 × 10−6
October	742	2.66	5.11	4.50	4.28	86.16	0.98	5.05 × 10−3	2.56 × 10−5
November	717	2.35	6.57	5.77	5.19	198.18	0.99	3.12 × 10−3	9.72 × 10−6
December	742	2.67	7.15	6.29	6.00	234.80	0.99	3.98 × 10−3	1.59 × 10−5
Yearly	8710	2.32	7.5	6.58	5.87	297.25	0.995	1.19 × 10−3	1.41 × 10−6

. No definite trend was observed in case of shape parameter; however, the scale parameter followed the monthly mean wind speed trend. The Weibull Mean wind speed or maximum energy carrying wind speed (V_m) varied from a minimum of 4.50 m/s in October to 9.63 m/s in June as given in column 5 of Table 3. This simply meant that in the month of June the maximum energy carrying wind speed was 9.63 m/s while in the month of October it was 4.50 m/s. On the other hand, the most probable wind speed (V_mp) in column 6 of Table 3 varied between 4.28 m/s and 10.02 m/s in the months of October and June; respectively. Here it can be said that in the month of June the most probable occurring wind speed was 10.02 m/s while 4.28 m/s in the month of October.

The wind power density (P_W) estimated using Weibull parameters is given in column 7 of Table 3. In general P_W values are found to be lower than P_A given in Table 2 above. In order to compare the P_W with P_A linear correlations are obtained by plotting the scatter diagrams, shown in Figure 1 and coefficient of determination values (R²) are determined for each month and the entire data set and are listed in column 8 of Table 3. Almost in all the months the R² values are found to be around 0.99 while RMSE and χ² of approximately 1 × 10⁻³ and 1 × 10⁻⁶, respectively. The magnitudes of these performance parameters indicate that the modeled and measured wind speed based wind power densities are in close agreement.

Maximum entropy density functions at low order moments 3, 4, 5, 6, 7, 8 and 9 were determined for monthly and overall periods and are summarized in

Table 4. Monthly comparison of actual wind power densities (P_A) with Weibull power densities (P_W) (Table 2) and power densities based on MEP-based function for orders 3–9 (P_E).

Order	January PA = 165.33 W/m2		February PA = 177.25 W/m2		March PA = 185.61 W/m2
	R2	PE (W/m2)	R2	PE (W/m2)	R2	PE (W/m2)
3	0.975	165.6	0.973	175.3	0.972	182.9
4	0.976	165.3	0.959	177.2	0.961	185.3
5	0.982	165.3	0.955	177.2	0.960	184.8
6	0.983	165.5	0.955	177.2	0.962	184.8
7	0.984	165.3	0.9554	177.2	0.961	184.8
8	0.984	165.3	0.9544	177.2	0.961	184.8
9	0.8614	224.64	0.9544	178.2	0.962	184.8
Order	April PA = 366.95 W/m2		May PA = 719.91 W/m2		June PA = 647.84 W/m2
	R2	PE (W/m2)	R2	PE (W/m2)	R2	PE (W/m2)
3	0.977	366.9	0.974	715.4	0.973	646.0
4	0.977	366.7	0.965	719.9	0.973	646.6
5	0.982	366.7	0.963	719.9	0.970	646.6
6	0.980	366.7	0.956	719.9	0.968	646.6
7	0.983	366.7	0.953	719.9	0.977	646.6
8	0.983	366.7	0.966	719.9	0.971	646.5
9	0.983	366.7			0.894	271.1
Order	July PA = 451.21 W/m2		August PA = 316.56 W/m2		September PA = 177.42 W/m2
	R2	PE (W/m2)	R2	PE (W/m2)	R2	PE (W/m2)
3	0.973	442.0	0.976	316.7	0.975	178.1
4	0.951	450.8	0.976	316.6	0.975	177.4
5	0.951	450.7	0.977	316.6	0.976	177.4
6	0.951	450.7	0.977	317.1	0.976	177.4
7	0.947	450.7	0.977	316.6	0.981	177.4
8	0.948	455.6	0.978	316.6	0.543	1475.6
9	0.430	624.0	0.978	316.6	0.881	1573.6
Order	October PA = 104.01 W/m2		November PA = 185.45 W/m2		December PA = 205.57 W/m2
	R2	PE (W/m2)	R2	PE (W/m2)	R2	PE (W/m2)
3	0.974	104.05	0.971	184.55	0.975	207.26
4	0.975	103.95	0.965	186.52	0.981	205.53
5	0.979	103.95	0.956	185.40	0.984	205.53
6	0.977	103.95	0.959	185.49	0.985	208.28
7	0.978	104.19	0.958	185.40	0.986	205.53
8	0.981	103.95	0.956	185.40	0.985	205.54
9	0.564		0.967	214.57	0.984	205.53

and

Table 5. Comparison of actual wind power densities (P_A) with Weibull power densities (P_W) and power densities based on MEP-based function for orders 3–9 (P_E).

Order	January
	PA = 309.25 W/m2
	PW = 297.25 W/m2
	R2	PE (W/m2)
3	0.974	304.7
4	0.962	308.2
5	0.962	309.2
6	0.966	309.4
7	0.968	309.2
8	0.968	309.2
9	0.968	309.2

, respectively. The wind power density values (P_E) obtained using lower order moments are in close agreement with each other. In most of the months the coefficient of determination values R² are found to be around 0.9 for all the monthly analysis and also for entire data set. The scatter diagrams between the P_A and P_E values for low order moments 5, 6, 7, and 8 along with the best fit linear line are shown in Figure 2a–d obtained using the entire data set. The goodness-of-fit test for maximum entropy function is performed using Kolmogorov–Smirnov (KS) test between the wind power density values (P_A and P_E) obtained using measured data and the maximum entropy density function. The test results indicate the acceptance of null hypothesis, as the critical value Q₉₅ = 0.01457 (for complete data set over the year with n = 8711 wind speed data points) calculated using Equation (15) is greater than KS test statistics Q = 0.643, calculated using Equation (14). Also in case of monthly analysis the critical value Q₉₅ = 0.04987 (for monthly data sets each of n = 744 wind speed data points) is greater than KS test statistics Q on monthly bases ranging from 7.5 × 10⁻⁴ to 8.3 × 10⁻⁴.

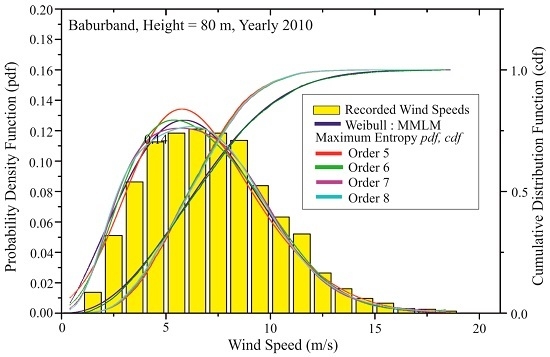
Figure 3 shows the histogram of measured wind speed data and overall probability plots of Weibull and maximum entropy functions for all four orders. A close look of probability plots for detailed analysis of wind speed data on monthly bases indicated that in general a better correlation is observed between the histograms and MEP-based functions compared to the Weibull function for all months. Furthermore, for majority of months all four orders showed a good agreement between measured data and the fitted function. Specifically, orders 5, 6 and 7 showed a better reliability of fit of MEP-based function to the measured wind speed data compared to orders 3, 4, 8 and 9. In case of a complete one year data set the correlation of Weibull and MEP based function with the histogram is comparable and is due to the fact that in case of a complete wind speed data set, the number of data points is much larger.

The wind power density values P_E (Table 4 and Table 5) are in close agreement with P_A values (column 8, Table 2) obtained using measured wind speed data compared to P_W values (column 7, Table 3) calculated using Weibull distribution function. For example in the month of May P_E is 719.88 W/m² while P_A and P_W values are 719.91 and 634.96 W/m², respectively. It is evident that P_E value is almost the same as P_A while P_W is way far from P_A. Similar type of comparisons is found for rest of the monthly and yearly values of wind power densities from two methods see Table 4 and Table 5.

Figure 4 shows that the wind power density values computed using Weibull functions are a bit different than the actual wind power density values for each month while those estimated using MEP-based function are comparable with actual power density values. This further proves that MEP-based function is more reliable for the estimation of the measured wind speed data distribution and subsequently the power density values. Although the authors have carried out a detailed analysis of measured wind speed data on monthly bases and have checked for the reliability of fit for the MEP-based function to the actual wind speed data distribution on all orders used (3, 4, 5, 6, 7, 8 and 9) but have found that there is a considerable deviation in the fit function above order 7. This may be attributed to the fact that on a monthly basis the data sample size is smaller compared to the entire year data set. The situation further aggravates as power densities are calculated for higher orders and becomes more pronounced for order 9 which show unrealistic values for some months.

In order to compute the energy generated by the chosen turbine, the continuous probability distribution of wind speed using Weibull and MEP-based function are integrated with the power characteristic curve of the turbine. The energy yield is calculated using NEG Micon NM60/250–1000 kW wind turbine. The technical specifications along with the wind power curve data are given in

Table 6. Selected wind turbine technical specifications.

NEG-Micon NM60/1000		Wind Turbine Power Curve Data
Turbine Specifications		Wind Speed (m/s)	Power (kW)	Wind Speed (m/s)	Power (kW)
Company	NEG Micon	2	0.00	12	873.70
Cut-in wind speed	3–4 m/s	3	1.70	13	954.40
Cut-out wind speed	20 m/s	4	36.70	14	1020.40
Rated wind speed	14 m/s	5	84.00	15	1037.80
Rated Power	1000 kW	6	142.20	16	1041.50
Rotor Diameter	60 m	7	263.00	17	1029.50
Swept area	2827.43 m2	8	399.20	18	1009.00
Tower Heights	50, 70, 80 a m m	9	540.70	19	988.60
No. of Blades	3	10	662.60	20	955.00
Grid Connection	50 Hz	11	761.30

^a Height used in this work.

. The power curve of the selected wind turbine is fitted to the Boltzmann Sigmoid function shown in Figure 5. Fitted parameters for the turbine using Boltzmann Sigmoid function (see Equation (25)) are A₁ = −0.06473, A₂ = 1.07611_, X₀ = 8.8478, d_x = 2.03981. In order to determine a relationship between energy available in the wind and the energy that is converted by a wind turbine, three interconnected factors related to wind turbine needs to be investigated. These factors i.e., wind turbine efficiency (ε), availability (Σ_F) and capacity factor (C_F), in conjunction with wind characteristics, characterize a wind turbine for the location under investigation.

The energy density (E_W), ideal wind energy (E_WTI), and actual wind energy (E_WTA) values calculated for each month and complete one year data set using Weibull function are summarized in

Table 7. Weibull wind energy estimation based on MMLM for Baburband at 80 m height for 2010.

Month	EW (kWh/m2)	EWTI (kWh)	EWTA (kWh)	ΣF (%)	ε (%)	Cp (%)
January	119,570.17	338,538.23	133,671.34	83.73	39.48	17.97
February	126,004.33	356,125.92	136,966.71	84.37	38.46	20.38
March	120,300.69	340,492.35	134,028.67	83.41	39.36	18.01
April	254,637.57	717,545.00	257,736.72	94.80	35.92	35.80
May	472,412.90	1,251,908.65	388,613.59	97.53	31.04	52.23
June	488,719.84	1,359,625.29	431,122.17	99.50	31.71	59.88
July	322,487.22	866,365.85	286,102.82	92.72	33.02	38.45
August	212,927.21	589,000.09	208,599.29	87.40	35.42	28.04
September	108,707.77	308,487.45	127,164.50	89.84	41.22	17.66
October	64,100.39	179,714.58	72,592.27	78.47	40.39	9.76
November	142,686.24	403,235.97	154,256.92	85.32	38.25	21.42
December	174,688.36	495,761.61	190,471.04	90.62	38.42	25.60
Yearly	2,589,341.21	7,180,159.69	2,543,819.30	88.69	35.43	29.20

. The corresponding values of availability factor, wind turbine efficiency, and the capacity factor are also included in this table. Table 7 summarizes the ideal wind energy (E_ETI), and actual wind energy (E_ETA) values calculated using MEP-based function for each month at orders 5 and 6 and for a complete one year data set for all four orders 5, 6, 7 and 8. In case of an ideal wind turbine with zero losses the available wind energy can be extracted completely. The energy density values estimated based on an ideal wind turbine are much larger than the values calculated using an actual wind turbine which depends upon the turbine performance curve operating between cut-in and cut-off wind speeds. As seen from the data given in Table 7 and

Table 8. Wind energy estimation using MEP-based function for Baburband at 80 m height for 2010.

Month	Order	PE (W/m2)	EETI (kWh)	EETA (kWh)	ΣF (%)	ε (%)	Cp (%)
January	5	165.33	345,779.85	140,325.93	82.60	40.58	18.86
February	5	177.19	356,632.30	136,124.74	82.69	38.17	20.26
March	5	184.81	393,864.22	153,697.09	88.74	39.02	20.66
April	5	366.71	764,513.71	272,350.77	95.03	35.62	37.83
May	6	719.88	1,365,916.96	421,387.76	99.74	30.85	56.64
June	6	646.56	1,292,576.75	414,454.94	99.10	32.06	57.56
July	5	450.66	905,567.28	291,349.70	96.43	32.17	39.16
August	5	316.56	697,281.38	241,927.65	89.66	34.70	32.52
September	5	177.35	364,861.16	151,408.45	91.22	41.50	21.03
October	5	103.95	218,130.97	90,157.89	84.56	41.33	12.12
November	5	185.40	375,076.48	145,948.15	81.90	38.91	20.27
December	5	205.53	431,017.39	171,457.92	85.00	39.78	23.05
Overall	5	309.25	7,370,569.89	2,576,830.62	90.14	34.96	29.58
	6	309.47	7,771,954.69	2,678,741.32	91.07	34.47	30.75
	7	309.25	7,334,653.69	2,588,934.37	89.73	35.30	29.72
	8	309.25	7,532,837.34	2,628,381.17	90.00	34.89	30.17

, the values of E_WTI and E_ETI are integral multiple of E_WTA and E_ETA values.

Furthermore, the data given in Table 7 and Table 8 suggests that the actual wind energy produced by a turbine in the month of May and June is higher than in the month of October, but the turbine efficiency for these months for both generating functions lay in the range of 30.85% and 32.06% which is less than the efficiency value in the month of October (40.39% and 41.33%). This apparent conflict between output power and efficiency can be explained by taking into consideration the availability and capacity factors. The availability factor for the months of May and June for both generating function was 97.53% and 99.74% which is much higher than that in the month of October i.e., 78.47% and 84.56%. At the same time the productivity of wind turbine or the capacity factor for May and June for both generating functions was 52.23% and 59.88% which is also higher than that of October i.e., 9.76% and 12.12%. Therefore in order to determine optimum energy output of a turbine and effectiveness of a potential site, all three turbine characteristics must be taken into account. The estimated efficiency values for all months and for the complete year data set are in conformity with the Betz limit.

In the light of above discussion, MEP-based function gives more realistic estimates of wind energy as compared to Weibull based function. Using MEP-based function, the highest estimate of wind energy using the chosen wind turbine is found to be 421,387.76 kWh (see column 5, Table 8) in the month of May and 90,157.89 kWh which is lowest in the month of October.

4. Conclusions

In this paper the Weibull distribution function and MEP-based functions are fitted to the recorded wind speed data at the Baburband wind site for the year 2010 on a monthly basis. In case of the Weibull function, MMLM is used to estimate the Weibull k and c parameters, whereas in the case of the MEP-based function seven fit orders are used, i.e., orders 3 to 9 for monthly wind speed data and for the entire data. A detailed study of the monthly wind speed data revealed that orders 5, 6 and 7 show good correlation with the measured wind speed data distribution as compared to orders 8 and 9. Additionally for the complete one year data set, MEP-based function using orders 5, 6, 7, 8 and 9 and Weibull function showed good correlation with the recorded wind speed data distribution.

Similarly, for monthly data sets it is observed that using the MEP-based function higher wind energy values were obtained for the fitted turbine as compared to Weibull-based function. However, the estimated values were realistic for orders 5, 6 and 7 for monthly data, whereas at higher orders the estimated values were significantly different compared with the measured values.

The application of the MEP-based function depends on the solution of the set of highly nonlinear equations (see Equation (5)). Furthermore, the presence of exponential and pre-exponential terms in equation leads to additional difficulties in the numerical solution of the problem. Additionally, calculated wind power density value is weighted by a pre-exponential term (see Equations (4), (5) and (16)), which for higher powers diverges and gives unrealistic value. A good fit of a theoretical distribution function to the measured wind speed data requires a good fit of the data as well as a good representation of wind power densities. In this present paper, while applying the MEP-based function to the measured wind speed data, the authors have employed moment orders from ranging from 1 to 9. In the present case MEP-based function with orders 1 and 2 completely failed to fit with the measured data and are not included in the analysis. The results obtained by applying MEP-based function with orders 3 to 9 for measured monthly and yearly wind data are shown in Table 4 and Table 5. A criterion for accepting a good fit distribution is set based on the maximum value of the evaluated coefficient of determination (R²-test) and additionally, the closest agreement of the calculated and actual power densities (P_W and P_A). Based on this criterion, it is observed that for majority of months the application MEP-based function at order 3 performed poorly both in terms of wind speed data (R²-test results) and wind power density see Table 4. The application of MEP-based function for the months of January, June, July, September and October using orders 9, 9, 9, 8, and 9, respectively, the R²-test values are in the range ~0.4–~0.8. For these cases the fitted distribution is said to be not reliable. Except for these months, the R²-test values at orders 4 to 9 are identical to the first decimal place (~0.9). In majority of months the application MEP-based function at order 7, the wind speed and wind power density representations are consistent with the behavior of the measured wind speed data. In general, moment orders 5 to 7 for the application of MEP-based function are suitable in terms of wind speed and power density, see Table 4. In case of measured wind speed data over entire year, since the statistically standard deviation decreases as $1/\sqrt{N}$, where N is the number of wind speed data points, the R²-test results are almost identical (see Table 4) for all orders namely 3 to 9. However, the wind power density representation at orders 3 and 4 are not in good agreement with the measured wind power density. Nevertheless, based on the same criteria the application of MEP based function at order 7 show consistency of the wind speed and wind power density representations with the measured wind speed data.

Although monthly and yearly R²-test result values are higher for the Weibull function as compared to the MEP-based function, for practical wind speed situations where calm spells or zero wind speeds exist at any site, the Weibull distribution always gives a zero value for pdf and fails to predict zero wind speed. Contrary to this using the MEP-based function, the pdf is consistent in predicting zero or calm wind speeds at any site. A complete and reliable fit of the measured wind speed data distribution would result in a reliable estimation of wind power density of a site under study, thereby giving reliable estimates of wind energy extracted using a wind turbine.