Shielding Effectiveness Simulation of Small Perforated Shielding Enclosures Using FEM

Abstract

Numerical simulation of shielding effectiveness (SE) of a perforated shielding enclosure is carried out, using the finite element method (FEM). Possibilities of model definitions and differences between 2D and 3D models are discussed. An important part of any simulation is verification of the model results—here the simulation result are verified in terms of convergence of the model in dependence on the degrees of freedom (DOF) and by measurements. The experimental method is based on measurement of electric field inside the enclosure using an electric field probe with small dimensions is described in the paper. Solution of an illustrative example of SE by FEM is shown and simulation results are verified by experiments.

1. Introduction

Nowadays, electronic devices contain a lot of highly energized parts, including processors, field-programmable gate arrays (FPGAs), power supplies and high-speed communications buses. But all these parts work on relatively low voltage levels and, therefore, they may often become victims of electromagnetic interference. One of its sources is high-speed data transmission. For these reasons, there exist many standards and recommendations concerning electromagnetically compatible environments. One part of electronic devices supporting a good level of EMC is electromagnetic shielding. Electromagnetic shielding mostly consists of shielding enclosures, gaskets, and ventilation structures. The shielding effectiveness (SE) is the term describing the quality of the shielding. There exist standards for SE measurement of shielding enclosures, but these standards do not respect the current trend—reduction of the device dimensions. For example, the IEEE standard for measuring the effectiveness of electromagnetic shielding enclosures [1] describes the measurement procedure for any enclosure having a smallest linear dimension greater or equal to 2.0 m. The question is, how to measure SE of such enclosures; the dimension of the measuring antenna depends on the wavelength and this antenna must be placed inside the shielding enclosures. If this is not possible, numerical or analytical methods can be used for determining SE. Analytical methods for SE calculation of the shielding enclosures with aperture are described in [2,3]. The numerical methods are well usable here, because it is easy to change geometry of the model. There are many suitable methods, including finite element method (FEM), method of moments (MoM), finite difference time domain method (FDTD) and others derived from them. Many papers can be found that deal with SE modelling—very interesting ones are [4,5,6,7]. This paper starts from previous articles [8,9,10] that are related to the problem of SE simulation.

1.1. Shielding effectiveness

The shielding effectiveness for electric and magnetic field is defined as the ratio (expressed in decibels) between the absolute value of electric field E₁ (or magnetic field H₁) at a point in space without the shielding and the absolute value of electric field E₂ (or magnetic field H₂) at the same point in space with the shielding [1]:

$${\mathrm{SE}}_{\mathrm{E}}=20\cdot \log \frac{\left|E_1\right|}{\left|E_2\right|}\begin{array}{}\end{array}\begin{array}{l}\left[\mathrm{dB}\right],\hfill \end{array}$$

(1)

$${\mathrm{SE}}_{\mathrm{H}}=20\cdot \log \frac{\left|H_1\right|}{\left|H_2\right|}\begin{array}{}\end{array}\begin{array}{c}\left[\mathrm{dB}\right]\end{array}$$

(2)

These definitions are applicable for theoretical calculations and for situation where dimensions of the measuring antenna are negligible compared with the dimensions of the measured shielding enclosure. In real measurement cases, however, the measuring antenna does not have negligible dimensions and the measured values depend on the location of the antenna inside the enclosure. This problem is caused by the cavity resonances of the enclosure that decrease the SE.

Similar problems exist for simulations—there it is necessary to use the definition where the field is integrated through the whole cavity of the enclosure. The global shielding effectiveness (GSEs) for an electric/magnetic field is defined by [11]:

$${\mathrm{GSE}}_{\mathrm{E}}=20\cdot \log \frac{{\displaystyle {\int }_V{E}_1\mathrm{d}V}}{{\displaystyle {\int }_V{E}_2}\mathrm{d}V}\begin{array}{}\end{array}\begin{array}{c}\left[\mathrm{dB}\right],\end{array}$$

(3)

$${\mathrm{GSE}}_{\mathrm{H}}=20\cdot \log \frac{{\displaystyle {\int }_V{H}_1\mathrm{d}V}}{{\displaystyle {\int }_V{H}_2\mathrm{d}V}}\begin{array}{}\end{array}\begin{array}{c}\left[\mathrm{dB}\right]\end{array}$$

(4)

Numerous factors decrease the SE of enclosures. There exist two most important factors: the first one is the cavity resonance of the box and the second one are the presence of apertures in the enclosure. The cavity resonance frequencies f_r are given by the formula [12]:

$$f_{\mathrm{r}}=\frac{1}{2\sqrt{\mathsf{\mu }\mathsf{\epsilon }}}\sqrt{{\left(\frac{m}{a}\right)}^2+{\left(\frac{n}{b}\right)}^2+{\left(\frac{p}{c}\right)}^2}\begin{array}{}\end{array}\begin{array}{c}\left[\mathrm{Hz}\right]\end{array}$$

(5)

where μ and ε represent the material parameters—permeability and permittivity of the cavity, a, b and c are the dimensions of the cavity (inside dimensions of the enclosure) and indexes m, n and p correspond to the resonance mode. The influence of the cavity resonances on SE is not easy to determine, because the influence of the field strength inside the cavity on the resonance depends on the quality factor Q of the resonator, which is often unknown.

Apertures in the enclosures have also a significant effect on the SE. The theoretical SE of a circular aperture with diameter r placed in a perfect shielding plate is [13]:

$${\mathrm{SE}}_{\mathrm{ap}}=20\cdot \log \frac{\mathsf{\lambda }}{2\mathsf{\pi }\cdot \mathrm{r}}\begin{array}{}\end{array}\begin{array}{c}\left[\mathrm{dB}\right]\end{array}$$

(6)

and the SE for structure with n apertures (where the distance between apertures is less than a half-wavelength) is given by [13]:

$${\mathrm{SE}}_{\mathrm{n}-\mathrm{ap}}=20\cdot \log \frac{\mathsf{\lambda }}{2\mathsf{\pi }\cdot \mathrm{r}\cdot \sqrt{n}}\begin{array}{}\end{array}\begin{array}{c}\left[\mathrm{dB}\right]\end{array}$$

(7)

One of the ways for obtaining a high SE of the shielding enclosure is using cable glands, shielded air vent panels (honeycomb structures), and shielding gaskets.

1.2. Definitions of Numerical Models

The most important numerical methods for SE simulation are the finite element method, finite difference time domain method, method of moments, and their modifications. The general geometries of the models are similar for all these methods, but the definitions—initial and boundary conditions, distribution of mesh—could be different. The model consists of a free space surrounding the excitation source and geometry of the shielding enclosure (see Figure 1). Of course, from the definition of the SE, there is necessary to calculate two models—one with the enclosure and one without it (only with the observation area of the same dimensions as the internal dimension of the enclosure).

The setting of correct boundary conditions of the model is necessary for obtaining correct results. For example, the model boundary is usually modeled as a perfect magnetic ($n\times H=0$) or electric ($n\times E=0$) conductor, but a better choice is to use perfectly matched layer (PML), where the transition of the source signal is improved. The boundary of the box should be modeled as a perfect electric conductor (PEC), when the material of the box is made from a highly conducting material. The definition of the source depends on the method used, and for FEM it is possible to use a source of electric or magnetic field.

The SE simulations can be solved in two or three dimensions. For a 2D simulation, it is necessary to compute two models represented by two slices of the enclosure. Two sets of results from 2D simulations exhibit results comparable with a 3D simulation. The main difference is in the solution time, the 3D simulation requires much longer time. On the other side, 2D FEM models can be calculated by a solver with hp-adaptivity of the mesh, which provides very accurate results [8].

2. 3D Finite Element Method (FEM) Numerical Model

For finite element analysis in the frequency domain, the governing wave equation can be written as:

$$\nabla \times \frac{1}{{\mathsf{\mu }}_{\mathrm{r}}}\left(\nabla \times E\right)=k_0^2\left({\mathsf{\epsilon }}_{\mathrm{r}}-\frac{j\mathsf{\sigma }}{{\mathsf{\omega }\mathsf{\epsilon }}_0}\right)E$$

(8)

where μ_r represents the relative permeability, ε_r stands for the relative permittivity, σ is electric conductivity, ε₀ represents the vacuum permittivity, and k₀ is the wave number of free space defined by the equation:

$$k_0=\mathsf{\omega }\sqrt{{\mathsf{\epsilon }}_0{\mathsf{\mu }}_0}=\frac{\mathsf{\omega }}{c}$$

(9)

The source is modeled as an electric point dipole, the vector of electric current dipole moment being $P=\left[0;0;1\right]$ $\mathrm{m}\cdot \mathrm{A}$.

The shielding box is approximated by a PEC, where:

$$n\times E=0$$

(10)

For the analysis of fringing fields, a sphere of air was added around the model that is overlaid with a perfectly matched layer (PML). PML absorbs all radiated waves with small reflections by stretching the virtual domains into the complex plane using the following coordinate transform for the general space variable t:

$$t\prime ={\left(\frac{t}{{\Delta }_{\mathrm{w}}}\right)}^n\left(1-i\right)\mathsf{\lambda }F$$

(11)

where Δ_w is the width of the PML region, n represents the PML order, λ is the frequency, and F denotes the scaling factor. The imaginary unit i satisfies the equation i² = − 1.

3. Illustrative Example

A rectangular prism shielding enclosure was used for this illustrative example of SE simulation. Its dimensions are 291 mm × 277 mm × 243 mm and the thickness of its wall is 1 mm. The circular aperture of 10 mm diameter is placed in the center of the area 277 mm × 243 mm (see Figure 2a). The cavity dimensions are 289 mm × 275 mm × 241 mm.

Figure 2b represents a spherical area of the FEM model. There are visible four regions, the first of them representing the PMLs (on the model boundary) followed by a free space (surrounding enclosure). Inside the free space region there are placed the excitation source and shielding enclosure. The model represents the worst case; radiation from the source impacts the wall with the aperture. All parts were computed using Equations (8)–(11) by the software COMSOL Multiphysics.

The FE mesh is shown in Figure 3. The size of the mesh was chosen with respect to the accuracy of the model—its important parts (shielding enclosure, free space area) were meshed more densely, while for PMLs we used sparser mesh. Five layers were used for modeling PMLs.

The model was solved in the frequency domain. The simulation started at 500 MHz and ended at 2500 MHz. The frequency step—with respect to the computation time—was chosen 2.5 MHz. Overall, 800 simulation runs were carried out.

Important part of the simulation is verification of the result accuracy. Computing of the total electric energy inside the model is one possibility to check the solution accuracy:

$${\mathrm{w}}_{\mathrm{e}}=\frac{{\mathrm{W}}_{\mathrm{e}}}{\mathrm{V}}\begin{array}{c}\begin{array}{}\end{array}\end{array}\begin{array}{c}{[\mathrm{J}/\mathrm{m}}^3]\end{array}$$

(12)

where V represents the whole volume of the model and energy W_e is calculated from the expression:

$${\mathrm{W}}_{\mathrm{e}}={\displaystyle \underset{V}{\int }\frac{1}{2}ED \mathrm{d}V}={\displaystyle \underset{V}{\int }\frac{1}{2}{\mathsf{\epsilon }}_0{E}^2 \mathrm{d}V\begin{array}{c}\begin{array}{}\end{array}\end{array}\begin{array}{c}\left[\mathrm{J}\right]\end{array}}$$

(13)

The accuracy of the solution is good if the total electric energy does not change with the number of the degrees of freedom (DOFs). For the same number of DOFs, the accuracy will be better for lower frequencies; much more DOF must be used for high frequencies. Figure 4 shows the dependences of total electric energies on the number of DOFs of the model. There are three dependences corresponding to frequencies 500 MHz, 1500 MHz and 2500 MHz. The accuracy of the result at 500 MHz is obviously good. Different situation occurs with frequency 1500 MHz; the good accuracy of result begins at 1.15 million of DOFs. The worst situation is at frequency 2500 MHz—the total electric energy of the model is changing and the accuracy of the result cannot be guaranteed. A model with more DOF must be solved for high frequencies. The solution of such a model with a high number of DOF, however, requires longer calculation time and higher demands on hardware.

Examples of simulation results are shown in Figure 5 and Figure 6. These figures represent distributions of electric fields in the model at frequencies 752.5 MHz and 1172.5 MHz. The frequency 752.5 MHz responds to the lowest resonance mode of the cavity (theoretically at frequency 752.94 MHz). Figure 5 represents a sectional view of the model. There can be seen its slices in the x-y plane and z-x plane, respectively.

There are visible minima and maxima of electric field inside the cavity; if the field is changing in any direction, it responds to resonance mode 1 (or higher) in the same direction. One change from minimum to maximum and again back to minimum (or inverse) represents one index of the resonance mode. No change of electric field responds to zero resonance mode indexes. The first resonance mode TE110 is at the frequency 752.5 MHz, (x-y-z axes, dimensions 289 mm × 275 mm × 241 mm). A 3D view of the same solution is shown in Figure 6.

Figure 7 shows the dependence of simulated GSE on frequency and theoretical SE of circular aperture placed in ideally shielding plate that is calculated from Equation (6). There are visible influences of cavity resonances on SE—drops on the GSE trace, which represent decreases of GSE. Each drop responds to one TE resonance mode of the cavity. Of course, no drops of SE occur in the theoretical dependence.

4. Measurement Methods

The shielding effectiveness is defined by Equations (1), (2) and the measurement methods are based on the following principle; there is measured electric (or magnetic) field at a point of the space with and without the shielding enclosure [14,15]. One measurement method with measuring antenna is shown in Figure 8.

There is no problem with shielding effectiveness measurement of large enclosures—there are standards for their measurement [1,16,17]. However, SE measurement methods are not unified [18]. On the other hand, shielding effectiveness measurement of small enclosures is quite problematic. The dimensions of the measurement antenna or electromagnetic field probe are not negligible—which depends on the wavelength—and this parameter is limiting factor for shielding effectiveness measurement of small enclosures, where it is necessary to place the measuring antenna inside the shielding enclosures. An antenna inside the enclosure represents another problem; the antenna represents filling of the cavity and it can influence the electromagnetic field inside it. The cavity filling influences space inside it and the resonance frequencies can be shifted.

The measurement should be performed in the far field region, where the characteristic impedance is conclusively defined; the theoretic distance is given by the expression:

$$r=\frac{\mathsf{\lambda }}{2\mathsf{\pi }}\begin{array}{}\end{array}\begin{array}{c}\left[\mathrm{m}\right]\end{array}$$

(14)

where r represents the transition between near and far fields and λ represents the wavelength.

In practice, the dimensions of the receiving antenna are often larger or comparable with the wavelength, and the distance between the near and far fields is defined by the Rayleigh criterion [19]:

$$r=\frac{2D^2}{\mathsf{\lambda }}\begin{array}{}\end{array}\begin{array}{c}\left[\mathrm{m}\right]\end{array}$$

(15)

where D represents the characteristic dimension of the receiving antenna.

5. Experimental Measurements

The experimental measurements were performed in the semi-anechoic chamber at the University of West Bohemia that is constructed for measurement at 3 m distance between the antenna and device under testing (DUT). This 3 m distance provides a uniform electromagnetic field in the frequency range from 26 MHz up to 18 GHz. The maximum value of electric field depends on the high-frequency power amplifier; for the 3 m distance we are able to produce 10 V/m in the frequency range from 80 MHz up to 3 GHz. Two types of HF power amplifiers are used: a FLH-200B (frequency range from 20 MHz to 1 GHz, maximum output power 200 W) and a FLG-30C (1–3 GHz, 30 W) and two types of antennas—BTA-M log periodic antenna (frequencies from 80 MHz to 2.5 GHz) and a BBHA 9120E horn antenna (500 MHz–6 GHz). For the measurement of electric field an ETS HI-6005 electric field probe was used.

The measurement method described in chapter Measurement Methods was used in this case, but the ETS HI-6005 electric field probe was replaced by a receiving antenna (see Figure 8). The BTA-M log periodic antenna radiates the power from amplifiers. The first measurement was performed without the shielding enclosure; the electric field strength was measured with the E-field probe. The second measurement was performed with the shielding enclosure; the E-field probe was inserted inside the box. The shielding effectiveness was calculated from measured values using Equation (1).

The frequency range of experimental measurement for the enclosure dimensions (Figure 2) is from 500 MHz to 2.5 GHz. The lowest frequency was set bellow the first cavity resonance of the enclosure. From the dimension of the cavity and Equation (5), the lowest cavity resonance frequency (and the first transversal electric mode TE110) is 752.94 MHz.

Figure 9 shows the experimental measurement in the semi-anechoic chamber. The shielding enclosure and optical cable from the electric field probe are visible in foreground (the paper box below the enclosure is the stand); the transmitting antenna and absorbers are visible in background. The optical cable was pulled through the cable gland representing a waveguide and the SE is not influenced by the next aperture in the shielding enclosure (the critical frequency of the waveguide is approximately 8.79 GHz).

6. Results Comparison

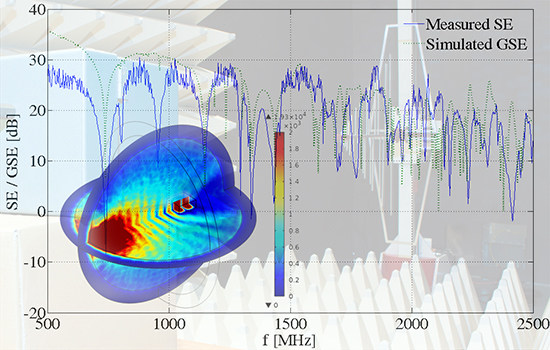
The simulated GSE dependence on frequency of the 3D model compared with the SE experimental measurement is shown in Figure 10. There is visible a good agreement of the resonance frequencies. These frequencies are possible to be calculated using Equation (5). Small differences between the calculated and measured (or simulated) frequencies are caused by the 2.5 MHz steps of measurement (or simulation).

The values of GSE are almost better than the measured values; it could be caused by using of the PEC boundary condition for the shielding enclosure.

The simulation results for frequencies higher 2 GHz are tentative, because the convergence of the model is not guaranteed (see Figure 4). The mean values are 23.39 dB for GSE and 23.59 dB for SE (the mean error being 0.2 dB).

The 2D model definitions are shown in Figure 11. The source representing an electric current dipole with current I₀ = 1 A is placed on the left. Absorbing boundary condition (ABC) was applied along the model boundary, which represents a free space surrounding model. The shielding box is approximated by a PEC.

The comparison between the 2D and 3D simulations of the GSE dependence on frequency is shown in Figure 12. The results from one 2D simulation are shown here, while other results of 2D simulations including results of the hp-adaptivity models were described in [8]. These results correspond with enclosure dimension 289 mm × 275 mm (it represents a slice of the 3D model in the z-axis). There are only TExx0 modes for 2D simulations; higher modes in the z-axis cannot be calculated. Another simulation (model which represents a y-axis slice of the 3D model) must be solved for determining of all TE modes.

7. Conclusions

This paper describes the problems with determining the shielding effectiveness of perforated shielding enclosures. General shielding effectiveness theory was defined for a perfect environment and conditions, but this theory does not correspond with real cases—these are influenced by dimensions of antennas (vs. spot observation points in general SE theory). For this reason a new definition called global shielding effectiveness (GSE) was established. Even when there exist standards for measurement of the SE, these are applicable only in certain cases, where large enclosures are examined, but these measurement methods are not applicable for very small enclosures having the smallest linear dimension smaller than 2.0 m.

Numerical methods can be helpful for determining of SE. There are lots of numerical methods (FEM, FDTD, MoM, etc.) which are used for SE calculations. The paper presents the FEM model of the perforated shielding enclosure, various definitions and geometries are discussed. The 3D model is supplemented with the complete set of results, while the 2D model only with a part of results. The disadvantage of 3D models is large hardware requirement and long solution time. 2D models are not time consuming. Also hp-adaptivity of FE mesh can be used for 2D models, in this case it is guaranteed the correctness of results (the convergence of the model from the mathematical viewpoint).

The verification of the numerical results using the total electric energy inside the model is an important part of the paper. The dependence of the total electric energy on DOF shows the solution accuracy; the model with more DOF must be solved for high frequencies (with the same accuracy as for low frequencies with a lower number of DOF). This solution, however, requires longer computational time and more powerful hardware. The simulation results were verified by measurements. Our measurement method uses a small electric field probe instead of receiving antenna, the dimensions of the probe correspond to a cube with 70 mm edge. The experimental measurement was performed in a semi-anechoic chamber and it was based on general SE theory (however, the dimensions of the electric field probe are not negligible—it is not a dot observation point). The probe dimensions allow SE measurement of a small shielding enclosure with dimensions of less than 2.0 m.

The miniaturization of electronic devices provides a space for SE numerical calculations—there are no possibilities for SE measurement (or very limited). The importance of numerical calculations for shielding effectiveness in the future, therefore, will grow. The future research will be focused on SE simulation and measurement of the complex perforated shielding enclosures, including ventilation structures or cable glands.