Next Article in Journal
Effect of Stand Density on Soil Organic Carbon Storage and Extracellular Enzymes Activity of Larch Plantation in Northeast China
Next Article in Special Issue
Ecological Adaptation of Two Dominant Conifer Species to Extreme Climate in the Tianshan Mountains
Previous Article in Journal
Physiology, Transcriptome and Root Exudates Analysis of Response to Aluminum Stress in Pinus massoniana
Previous Article in Special Issue
Differences in the Responses of Tree-Ring Stable Carbon Isotopes of L. sibirica and P. schrenkiana to Climate in the Eastern Tianshan Mountains
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Forests
Volume 14
Issue 7
10.3390/f14071411
forests-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Daily Climatic Data Better Explain the Radial Growth of Swiss Stone Pine (Pinus cembra L.) in High-Elevation Cliffs in the Carpathians

by
Katarzyna Izworska
1,2,*,
Tomasz Zielonka
1,
Paweł Matulewski
3 and
Elżbieta Muter
4
1
Institute of Biology and Earth Sciences, Pedagogical University of Cracow, Podchorążych 2, 30-084 Kraków, Poland
2
W. Szafer Institute of Botany, Polish Academy of Sciences, Lubicz 46, 31-512 Kraków, Poland
3
Institute of Geoecology and Geoinformation, Faculty of Geographical and Geological Sciences, Adam Mickiewicz University, B. Krygowskiego 10, 61-680 Poznań, Poland
4
Department of Forest Biodiversity, Faculty of Forestry, University of Agriculture in Krakow, 29 Listopada 46, 31-425 Kraków, Poland
*
Author to whom correspondence should be addressed.
Forests 2023, 14(7), 1411; https://doi.org/10.3390/f14071411
Submission received: 20 June 2023 / Revised: 7 July 2023 / Accepted: 8 July 2023 / Published: 11 July 2023
(This article belongs to the Special Issue Response of Tree Rings to Climate Change and Climate Extremes)
Browse Figures
Versions Notes

Abstract

:
Information about climate–growth relationships is crucial for predicting the potential climatic impact on tree species, especially those growing on the edges of their distribution range, for instance, in high-elevation forests. This study aimed to determine changes in the relationships between tree-ring widths and daily climatic data in high-elevation forests in the Western Carpathians over time. Climate–growth relationships were calculated to obtain the TRWI (tree-ring-width index) chronology (based on 104 trees) and day-wise aggregated data for temperature (mean, minimum, and maximum) and sums of precipitation. The radial growth of stone pine was mostly determined by the mean temperature in the period between mid-June (21st) and the beginning of July (4th) for the critical 14-day window width (r = 0.44). The negative influence of precipitation on the radial growth occurred in summer (r = −0.35) and overlapped with the period of the positive influence of temperature. Dendroclimatic studies based on daily data may define the exact periods (expressed in calendar days) that influence the radial growth of trees much better than the commonly used monthly means. This is particularly important in analysing the growth of trees at high elevations, where the climatic factor strongly limits radial growth.

Graphical Abstract

1. Introduction

Climate change is a phenomenon observed worldwide in recent times. It is related to increases in annual temperature and the distribution of precipitation [1,2,3]. Although we are still far from the Holocene climatic optimum, recent models predict further progress towards higher temperature and lower precipitation [4,5,6].
Thus, it is predicted that the distribution range of tree species will be changing parallel to climate change. The possible delays in tree responses will be minor or the range changes will be unable to keep up with climate change; therefore, the adaptation of species in accordance with environmental conditions will significantly worsen [7,8,9,10,11]. The frequency and intensity of extreme climatically induced events are also expected to change [4,12,13]. Climate change is widespread, affecting forests within a variety of geographical regions where warmth (e.g., in mountain or boreal ranges) or water availability (e.g., in arid and Mediterranean areas) are limiting environmental factors [13]. Trees on the edge of their distribution range are subjected to environmental stress, and their growth response to climate can reveal ecological thresholds beyond which they may not be able to persist. This information is critical for predicting the potential impacts of climate change on the distribution of tree species and the vitality of species populations.
Moreover, climate impacts on forests range from single extreme events with a difficult-to-predict time and location, to more obvious gradual changes. Therefore, it is necessary to conduct research on different spatial scales, from local to global, with the use of data of varying resolutions and species. Retrospective tree-ring-based studies are a useful tool for investigating how trees may adapt to forecasted changes [5,14,15,16]. A long-living organisms exposed to environmental variability, trees seem to be the best indicators of the reactions of living organisms to climate change [14,15]. This is especially important for trees growing on the edge of their distribution range, such as the north and upper timberlines.
High-elevation forests are the sentinels of change due to their location at the edges of their distribution range. They react quickly and strongly to environmental changes, including climate [17]. Extreme weather conditions are common in high-elevation ecosystems, due to the large amplitude of day–night and seasonal temperatures [17,18,19]. A low nutrient supply, as well as significant disruptions produced by gravity—rock and avalanche, snowfall and snow accumulation, and winds—contribute to the harsh environment of cliffs [17]. The Swiss stone pine (Pinus cembra L.) is a taxon with scattered populations (the Alps and Carpathian Mountains), exhibiting the finest adaptations for colonisation and growth in high-elevation cliffs [9,20,21,22,23,24]. Previous studies from the Alps [9,24,25,26] and Carpathian Mountains [20,27,28] have shown that the response of this species to climate changes is not stable over time.
The analysis of the relationship between radial growth and climate has typically been carried out using monthly meteorological data, e.g., [25,26,29,30]. Such data can provide a broader perspective on the long-term relationship between growth and climate, as it captures seasonal and annual fluctuations in environmental conditions. It is useful to identify general patterns and trends in growth responses to climate variables over time. However, it is important to consider the limitations of monthly data and its disadvantage to miss short-term climatic effects. Nevertheless, most of these studies have used the mean monthly climatic data when the months are artificially time-compressed [31,32,33]. Methodological improvements, access to gridded climate datasets and computing power to manage big databases have allowed for conducting more comprehensive studies with high-resolution data sets [16]. Daily climatic data offer a more detailed view of environmental conditions, which can help identify subtle effects of climate on tree growth that may be missed with monthly data. The daily resolution of climatic data detects the exact days of the year when temperature and precipitation significantly influence the radial growth of trees [32,33]. Overall, the use of daily climatic data can be valuable in analysing climate–growth relationships, but it requires careful consideration of advantages and disadvantages and the research question addressed.
This study aimed to enhance the precision and temporal resolution of the climate–growth correlation for Swiss stone pine in an extreme environment of highly elevated cliff forests. Specifically, we aimed to (1) examine climate–growth relationships using a daily response function, (2) determine the exact days of the year in which climatic parameters significantly affect growth, and (3) explore how the growth response to climate changes over time (throughout the last 90 years). It was hypothesised that the strength of the climate–growth relationship decreased in the warming climate over the last decades.

2. Materials and Methods

2.1. Study Area and Climate

The study site was located in the upper treeline ecotone in the Tatras (the Western Carpathian Mountains) (49°12′54.48″ N; 20°4′34.68″ E) (Figure 1). The Tatra Mountains, having classic alpine terrain and elevations of over 2600 m a.s.l., represent the highest and most rugged Carpathian mountain range [22,34]. The studied stone pines grow in high-elevation cliff forests on steep, granite slopes (ca. 70–80°) between the subalpine zone and dwarf pine scrub (Pinus mugo Turra) (ca. 1480 m a.s.l.). The study area was described in detail in the previous paper analysing the same tree samples [20]. It is a protected area of the Tatra National Park under a temperate-continental climate zone with significant differences between the daily maximum and minimum temperature and large amounts of precipitation [34]. The annual mean temperature of the sample site was 3.32 °C covering the period of 1921–2009, and the sum of annual precipitation was 1212 mm (Figure 2a,b).

2.2. Tree-Ring and Climatic Data

The increment cores were extracted at breast height (ca. 1.3 m) from stone pine trees growing in the study area with a Pressler borer. The cores were labelled, sanded, and then scanned at a 2400 DPI resolution. The ring widths were measured using the WinDendro software (https://www.regentinstruments.com/assets/windendro_about.html (accessed on 21 April 2023)). The accuracy of cross-dating was checked with COFECHA [36,37]. Time series that did not correlate with others were excluded to avoid potential errors in cross-dating. The diameter at breast height (DBH), height, and age of the studied trees as well as the tree-ring width (TRW) chronology characteristics were comprehensively described by Izworska et al. [20].
Daily climatic data: Temperature (mean, maximum, and minimum) and a sum of precipitation were obtained from the closest grid point for the study site (49°12′54.48″ N; 20°4′34.68″ E) from the E-OBS gridded climate dataset [38]. E-OBS version 25.0e (0.1-degree regular grid) covers the time from 1 January 1920 to now.

2.3. Analysis of Daily Climate–Growth Relationships

Climate–growth relationships were calculated using residual chronology (TRWI—tree-ring-width index) for the 1921–2009 period. To remove the age-related growth trends and competition effect, detrending was performed using the spline function (frequency response of 0.50 and cut off at 0.67 series length) in the ‘dplR’ (in R version 4.0.0) [39,40]. Statistics of the detrended chronology for the climate analysis (1921–2009), including interseries correlation (Rbar), expressed population signal (EPS), subsample signal strength (SSS) [41], and mean sensitivity (MS) [42], were calculated using the ‘dplR’ with the ‘rwi.stats’ functions [43].
Climate–growth relationships for the TRWI chronology and day-wise data for temperature (mean, maximum, and minimum) and the sum of precipitation during the 1921–2009 period, and the two subperiods of 1921–1965 and 1966–2009, were analysed. These subperiods were chosen as a comparable length (45 years and 44 years, respectively) series out of the 89-year climatic data to indicate possible changes in the growth reaction due to climate change over the last decades. We used the ‘daily_response()’ function from the ‘dendroTools’ [31,40]. The primary objective of the ‘daily_response()’ function was to examine changes over time in the relationships between tree rings and daily climatic data. The function used a moving window through daily data and aggregated data within each window by calculating its averages and then calculating statistical metrics (i.e., correlation coefficient). The moving window was based on the window width (number of days) and daily data within the position of the matrix [31]. The daily correlations were computed by taking into account all window widths ranging from 7 to 210 consecutive days from July of the previous year to September of the year of growth. To calculate partial correlations, a bootstrap procedure was applied within 1000 replicates.

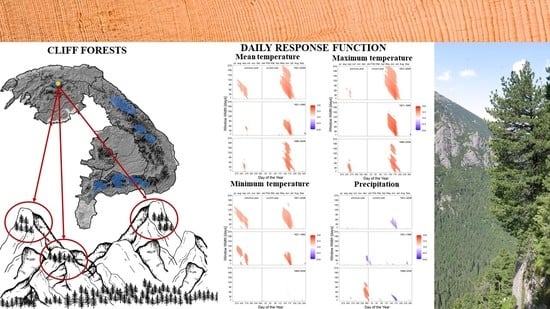
3. Results

3.1. Site-Specific Chronology

The TRWI chronology for the 1921–2009 period covered the available daily climatic data (Figure 3); the statistical parameters are provided in Table 1. The chronology shows the EPS value, as well as SSS exceeding the threshold of 0.85, indicating the strong climate signal in the site chronology and allowing us to conduct further climatic analyses [44,45]. The relatively low value of Rbar might be because our sampled trees were not a homogenous group with a large number of samples (104 trees). Alongside that, the trees were of different ages and growing in various microhabitats, reflecting individual growth conditions in the cliffs. Rbar values are usually higher in more homogenous groups/areas.

3.2. Climate–Growth Relationships

3.2.1. Mean Temperature

The highest positive significant correlation coefficient (r = 0.44) between the TRWI chronology and the mean temperature was found for the 14-day window width between 21 June and 4 July (DOY 172–185) during the year of growth (Figure 4). However, an important period with a high correlation (r > 0.40) was found for the window width range between 14 and 50 days, spanning mid-June to the beginning of August (DOY 168–222). Additionally, tree growth was positively influenced by the mean temperature of autumn the previous year (0.20 < r < 0.30), and an important period with relatively high correlation coefficients for this period spanned mid-September to the end of October (DOY 257–306; 39–46-day window width) (Figure 4).
In the first subperiod (1921–1965), the highest positive significant correlation coefficient (r = 0.51) between the TRWI chronology and the mean temperature was found for the 29-day window width between 21 June and 19 July (DOY 172–200) during the year of growth (Figure 4). The period with a high correlation (r > 0.40) was found for the window width range between 10 and 33 days and spanned the end of June to the end of July (DOY 172–211). Tree growth was positively influenced by the mean temperature of autumn the previous year (0.30 < r < 0.40), and an important period with relatively high correlation coefficients was found for the period spanning the end of September to mid-November (DOY 272–316; 35–43-day window width) (Figure 4).
In the second subperiod (1966–2009), the highest positive significant correlation coefficient (r = 0.44) between the TRWI chronology and the mean temperature was found for the 14-day window width between 20 June and 3 July (DOY 171–184) during the year of growth (Figure 4). The period with a high correlation (r > 0.40) was found for the window width range between 14 and 47 days and spanned mid-June to the beginning of August (DOY 168–218). Tree growth was positively influenced by the mean temperature of autumn the previous year (0.30 < r < 0.40), and an important period with relatively high correlation coefficients was found for the period spanning mid-September to the end of October (DOY 256–300; 23–43-day window width) (Figure 4).

3.2.2. Minimum Temperature

The highest positive significant correlation coefficient (r = 0.37) between the TRWI chronology and the minimum temperature was found for the 14-day window width between 21 June and 4 July (DOY 172–185) during the year of growth (Figure 5). However, an important period with a high correlation (r > 0.35) was found for the window width range between 14 and 38 days, spanning mid-June to the end of July (173–192). Additionally, tree growth was positively influenced by the minimum temperature at the end of summer and autumn the previous year (0.25 < r < 0.30). There were two important periods with relatively high correlation coefficients (r > 0.25), spanning the end of September to the end of October (DOY 267–302, 30–35-day window width) and mid-August to the first days of November (DOY 232–307; 64–70-day window width) (Figure 5).
In the first subperiod (1921–1965), the highest positive significant correlation coefficient (r = 0.49) between the TRWI chronology and the minimum temperature was found for the 13-day window width between 22 June and 4 July (DOY 173–185) during the year of growth (Figure 5). However, an important period with a high correlation (r > 0.45) was found for the window width range between 11 and 23 days, spanning the end of June to the end of July (DOY 171–202). There were two important periods with relatively high correlation coefficients (r > 0.33), spanning the end of September to mid-November (DOY 272–324, 7–50-day window width) and mid-August to mid-November (DOY 231–316; 73–83-day window width) (Figure 5).
No distinct impact of minimum temperature was observed in the second subperiod (1966–2009) during the year of growth and the previous year (Figure 5).

3.2.3. Maximum Temperature

The highest positive significant correlation coefficient (r = 0.48) between the TRWI chronology and the maximum temperature was found for the 38-day window width between 21 June and 28 July (DOY 172–209) during the year of growth (Figure 6). However, an important period with a high correlation (r > 0.44) was found for the window width range between 14 and 55 days, spanning mid-June to the beginning of September (DOY 160–250). Additionally, tree growth was positively influenced by the maximum temperature of autumn the previous year (0.20 < r < 0.26), and an important period with relatively high correlation coefficients was found for the period spanning mid-September and mid-November (DOY 256–315; 23–58-day window width) (Figure 6).
In the first subperiod (1921–1965), the highest positive significant correlation coefficient (r = 0.56) between the TRWI chronology and the maximum temperature was found for the 39-day window width between 21 June and 29 July (DOY 172–210) during the year of growth (Figure 6). However, an important period with a high correlation (r > 0.45) was found for the window width range between 15 and 45 days, spanning mid-June to the beginning of August (DOY 169–222). No significant impact of maximum temperature was observed in the first period of the previous year (Figure 6).
In the second subperiod (1966–2009), the highest positive significant correlation coefficient (r = 0.45) between the TRWI chronology and the maximum temperature was found for the 14-day window width between 20 June and 3 July (DOY 171–184) during the year of growth (Figure 6). However, an important period with a high correlation (r > 0.33) was found for the window width range between 11 and 55 days, spanning the end of June to mid-August (DOY 171–225). Additionally, tree growth was positively influenced by the maximum temperature of autumn the previous year (0.37 < r < 0.46), and an important period with relatively high correlation coefficients was found for the period spanning between mid-September and mid-October (DOY 255–292; 12–36-day window width) (Figure 6).

3.2.4. Precipitation

The strongest negative significant correlation coefficient (r = −0.35) between the TRWI chronology and the sum of precipitation was found for the 15-day window width between 19 June and 3 July (DOY 170–184) during the year of growth (Figure 7). An important period with a strong correlation coefficient (r < −0.33) was found for the window width range between 13 and 21 days, spanning mid-June to mid-July (DOY 169–192). No distinct impact of precipitation was observed in the previous year (Figure 7).
In the first subperiod (1921–1965), the strongest negative significant correlation coefficient (r = −0.38) between the TRWI chronology and the sum of precipitation was found for the 39-day window width at the turn of the year from 25 December to 2 February (DOY 360–33) (Figure 7). An important period with a strong correlation coefficient (r < −0.30) was found for the window width range between 27 and 54 days, spanning the end of December to mid-February (DOY 358–49) (Figure 7).
In the second subperiod (1966–2009), the strongest negative significant correlation coefficient (r = −0.53) between the TRWI chronology and the sum of precipitation was found for the 15-day window width in the period between 19 June and 3 July (DOY 170–184) during the year of growth (Figure 7). An important period with strong correlation coefficients (r < −0.40) was found for the window width range between 11 and 20 days, spanning mid-June to mid-July (DOY 168–194). Additionally, the period with significant correlation coefficients (r > 0.40) was found for the window width range between 52 and 63 days, spanning mid-December to the end of February (DOY 348–54) (Figure 7).

4. Discussion

This is the first study that analyses the potential of applying daily climatic variables to enhance the precision and temporal resolution of the climate–growth correlation for stone pine in the Western Carpathians. Most previous dendroclimatic studies about the growth of Pinus cembra were based on monthly climatic data. Papers about the radial growth of stone pine discuss higher altitudes of the Alps and Carpathians [20,24,25,26,27,28,46,47]. Only a few authors used daily data for the dendroclimatic study and mostly with reference to wood anatomy. Day-wise aggregated climatic data were used by Știrbu et al. [48] for the South-Western Carpathians and Carrer et al. [23] for the Eastern Alps to analyse xylem anatomical traits, maximum density (MXD), and the ring widths of stone pine.
From another perespective, summer temperature remains a key limiting factor of stone pine growth at higher elevations. Our analyses clearly show that the most important period for radial growth of stone pine is limited to two–three weeks in the second half of June and the first half of July, when the correlations between the ring widths and temperature are the strongest. By expanding the number of analysed days (the window width), significant reactions were found for the period between mid-June and the beginning of August (with a lower correlation coefficient). A similar pattern was found in the Alps and Carpathians, where the temperature from mid-June to the beginning of July was the most important factor for radial growth and explained by favourable conditions for the cell number and tangential cell-wall thickness. The radial cell-wall thickness was positively correlated with the temperature of a later period (from mid-July to the beginning of September) [23,48]. The lumen area was negatively correlated with the temperature from the end of June to the end of August [48]. The TRW analysed in this study was a parameter, which comprised all anatomical features; thus, the relationship between TRW and daily temperature data is not so strong. The changes in the growth–temperature relationship over time were more obvious when analysing the maximum and minimum daily temperatures. The minimum daily temperature, known as the night-time low, is probably the closest indicator limiting tree growth at high elevations [42]. The warmer day-time temperature cannot compensate for the cold nights, and what is more, the low minimum temperature in spring can delay the growing season [49]. The biggest difference between the subperiods of 1921–1965 and 1966–2009 was obvious for minimum temperatures. In the first period the minimum temperature of summer positively and significantly influenced the growth; while in the second subperiod, the minimum temperature lost its relevance. It is possible that the minimum temperature was greater than the threshold for affecting tree growth in the second subperiod.
The association between growth and the temperature of autumn the previous year is also well documented in the literature [25,46,50,51,52]. Our study allowed us to determine the period of importance more precisely. The most positive temperature occurred during the time between mid-September and mid-October of the previous year, but this interval expanded from the beginning of August to the beginning of November once the minimum temperature is taken into consideration. The crucial role of the autumn temperature results from the timing period was the bud set and the accumulation of reserves for building effective protection against winter frost, drought, or wind [18,53,54,55]. However, this pattern changed over time when considering shorter subperiods and the minimum and maximum temperatures. For example, this relationship disappeared for maximum temperatures in the years 1921–1965, which can be related to the cooler autumn during this period; however, it becomes clear in the second half of the 20th century when the maximum temperatures of autumn were higher. Our analysis did not reflect the temperature of the soil, which is crucial for the physiological activity of trees within their distribution limits (upper timberline), as soil retains heat for several days during unfavourable weather conditions, especially in autumn when trees enter dormancy [49,56].
Our research confirmed that summer precipitation had a negative influence on tree growth at high elevations [20,24,26]. In our study, this period of negative correlations almost completely overlaps with the days with the highest positive influence of the temperature and lasts between mid-June and the beginning of July. This relationship was not clear in the first half of the 20th century (1921–1965), which can be attributed to the lower precipitation during this time (Figure 2b). It is noteworthy that the radial growth of stone pine was influenced by winter precipitation from the preceding vegetation season during the shorter analysed periods. Additionally, the negative impact of winter precipitation on radial growth observed in the first subperiod (1921–1965) became positive in the second subperiod (1966–2009). The same trend was observed in the Alps [26,50]. This shift may be due to changes in precipitation patterns, possibly because of the amount and timing of precipitation having shifted. It is possible that warmer temperature during the dormant season with higher precipitation results in substantial snow depth, which can help prevent deep soil frost and mitigate the risk of damage caused by frost drought [17].
The general outcome of our study was that temperature became less important as a growth factor at high elevations in the Carpathians, which confirmed our hypothesis. The change in the temperature may potentially promote an upward shift of this species in the Tatra Mountains. Our study essentially validated the conclusions of Briffa et al. [57], Paulsen et al. [58], and Körner and Hoch [49]: The climate pattern fluctuates and reflects a threshold response. As the climate continues to warm, the treeline is also shifting upslope. One of the biggest challenges is to determine the rate and range at which local tree limits align with the warming climate [49]. As a result, trees that once grew within the treeline are now exposed to conditions that no longer resemble their boundary from the past. It means that stone pine in the Tatras has been growing in better climatic conditions over the last decades due to the shifting climatic treeline [59]. The warming climate opens space for the colonisation of higher elevations, and stone pine may benefit from these changes. As a zoochoric species dispersed by nutcracker (Nucifraga caryocatactes), stone pine can migrate upslope. This is especially important for the species due to their relatively small and fragmented, but stable, population with a significant degree of genetic variability in the Western Carpathians [22,60,61,62].

5. Conclusions

Our study showed that the temperature between mid-June and the beginning of July was a key factor for the growth Swiss stone pine in cliffs. The reaction of trees to climate was not stable over time. The changes in the growth–temperature relationship are the clearest with the minimum daily temperature. The negative influence of precipitation on growth almost completely overlaps in time with the highest positive influence of temperature (mid-June to beginning of July). Therefore, the potential migration of Pinus cembra to higher elevations is promoted by climate warming.
Dendroclimatic studies based on daily data define the periods (exact calendar days) that influence the radial growth of trees more precisely than monthly data. This is especially important in analysing the growth of trees at high elevations, where the vegetation season is short, and the climate factor strongly limits radial growth. Finally, the forest stands near the treeline are prone to climate change, and daily climatic data allow us to track these changes with a higher resolution.

Author Contributions

Conceptualization, K.I., T.Z. and E.M.; Data curation, K.I. and P.M.; Formal analysis, K.I.; Investigation, K.I., T.Z. and E.M.; Methodology, K.I. and E.M.; Resources, T.Z.; Visualization, K.I. and P.M.; Writing—original draft, K.I., T.Z. and E.M.; Writing—review and editing, K.I., T.Z. and E.M. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

Data will be made available on request.

Acknowledgments

We are grateful to Natalia Dubaj for help with fieldwork and laboratory assistance. We would like to thank the reviewers whose comments improved the paper.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Adler, C.; Wester, P.; Bhatt, I.D.; Huggel, C.; Insarov, G.; Morecroft, M.; Muccione, V.; Prakash, A.; Alcántara-Ayala, I.; Allen, S.K.; et al. Cross-Chapter Paper 5: Mountains. In Climate Change 2022: Impacts, Adaptation and Vulnerability. Contribution of Working Group II to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Pörtner, H.O., Roberts, D.C., Tignor, M., Poloczanska, E.S., Mintenbeck, K., Alegría, A., Craig, M., Langsdorf, S., Löschke, S., Möller, V., et al., Eds.; Cambridge University Press: Cambridge, NY, USA, 2022; pp. 2273–2318. [Google Scholar] [CrossRef]
  2. Esper, J.; Klippel, L.; Krusic, P.J.; Konter, O.; Raible, C.C.; Xoplaki, E.; Luterbacher, J.; Büntgen, U. Eastern Mediterranean summer temperatures since 730 CE from Mt. Smolikas tree-ring densities. Clim. Dyn. 2020, 54, 1367–1382. [Google Scholar] [CrossRef]
  3. Chen, D.; Rojas, M.; Samset, B.H.; Cobb, K.; Diongue Niang, A.; Edwards, P.; Emori, S.; Faria, S.H.; Hawkins, E.; Hope, P.; et al. Framing, Context, and Methods. In Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Masson-Delmotte, V., Zhai, P., Pirani, A., Connors, S.L., Péan, C., Berger, S., Caud, N., Chen, Y., Goldfarb, L., Gomis, M.I., et al., Eds.; Cambridge University Press: Cambridge, NY, USA, 2021; pp. 147–286. [Google Scholar] [CrossRef]
  4. Beniston, M.; Keller, F.; Koffi, B.; Goyette, S. Estimates of snow accumulation and volume in the Swiss Alps under changing climatic conditions. Theor. Appl. Climatol. 2003, 76, 125–140. [Google Scholar] [CrossRef] [Green Version]
  5. Frank, D.; Esper, J. Characterization and climate response patterns of a high-elevation, multi-species tree-ring network in the European Alps. Dendrochronologia 2005, 22, 107–121. [Google Scholar] [CrossRef]
  6. Zscheischler, J.; Westra, S.; van den Hurk, B.J.; Seneviratne, S.I.; Ward, P.J.; Pitman, A.; AghaKouchak, A.; Bresch, D.N.; Leonard, M.; Wahl, T.; et al. Future climate risk from compound events. Nat. Clim. Chang. 2018, 8, 469–477. [Google Scholar] [CrossRef]
  7. Babst, F.; Bouriaud, O.; Poulter, B.; Trouet, V.; Girardin, M.P.; Frank, D.C. Twentieth century redistribution in climatic drivers of global tree growth. Sci. Adv. 2019, 5, eaat4313. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  8. Camarero, J.J.; Linares, J.C.; Sangüesa-Barreda, G.; Sánchez-Salguero, R.; Gazol, A.; Navarro-Cerrillo, R.M.; Carreira, J.A. The multiple causes of forest decline in Spain: Drought, historical logging, competition and biotic stressors. In Dendroecology; Amoroso, M., Daniels, L., Baker, P., Camarero, J.J., Eds.; Springer: New York, NY, USA, 2017; pp. 307–323. [Google Scholar] [CrossRef]
  9. Casalegno, S.; Amatulli, G.; Camia, A.; Nelson, A.; Pekkarinen, A. Vulnerability of Pinus cembra L. in the Alps and the Carpathian Mountains under present and future climates. For. Ecol. Manag. 2010, 259, 750–761. [Google Scholar] [CrossRef]
  10. Dyderski, M.K.; Paź, S.; Frelich, L.E.; Jagodziński, A.M. How much does climate change threaten European forest tree species distributions? Glob. Chang. Biol. 2018, 24, 1150–1163. [Google Scholar] [CrossRef]
  11. Lindner, M.; Maroschek, M.; Netherer, S.; Kremer, A.; Barbati, A.; Garcia-Gonzalo, J.; Marchetti, M. Climate change impacts, adaptive capacity, and vulnerability of European forest ecosystems. For. Ecol. Manag. 2010, 259, 698–709. [Google Scholar] [CrossRef]
  12. Allen, C.D.; Macalady, A.K.; Chenchouni, H.; Bachelet, D.; McDowell, N.; Vennetier, M.; Kitzberger, T.; Rigling, A.; Breshears, D.D.; Hogg, E.H. (Ted); et al. A global overview of drought and heat-induced tree mortality reveals emerging climate change risks for forests. For. Ecol. Manag. 2010, 259, 660–684. [Google Scholar] [CrossRef] [Green Version]
  13. Spinoni, J.; Vogt, J.V.; Naumann, G.; Barbosa, P.; Dosio, A. Will drought events become more frequent and severe in Europe? Int. J. Climatol. 2018, 38, 1718–1736. [Google Scholar] [CrossRef] [Green Version]
  14. Schweingruber, F.H. Tree Rings and Environment: Dendroecology; Haupt-Verlag: Bern, Switzerland, 1996; p. 609. [Google Scholar]
  15. Speer, J.H. Fundamentals of Tree-Ring Research; University of Arizona Press: Tucson, AZ, USA, 2010; p. 368. [Google Scholar]
  16. Pearl, J.; Keck, J.; Tintor, W.; Siekacz, L.; Herrick, H.; Meko, D.; Pearson, C. New frontiers in tree-ring research. Holocene 2020, 30, 923–941. [Google Scholar] [CrossRef]
  17. Körner, C. Alpine Treelines: Functional Ecology of the Global High Elevation Tree Limits; Springer: Berlin/Heidelberg, Germany, 2012; p. 220. [Google Scholar]
  18. Tranquillini, W. Physiological ecology of the alpine timberline. In Ecological Study; Springer Nature: Berlin/Heidelberg, Germany; New York, NY, USA, 1979; Volume 31, pp. 1–137. [Google Scholar]
  19. Körner, C.; Paulsen, J.A. World-wide study of high altitude treeline temperatures. J. Biogeogr. 2004, 31, 713–732. [Google Scholar] [CrossRef]
  20. Izworska, K.; Muter, E.; Matulewski, P.; Zielonka, T. Tree rings as an ecological indicator of the reaction of Swiss stone pine (Pinus cembra L.) to climate change and disturbance regime in the extreme environment of cliff forests. Ecol. Indic. 2023, 148, 110102. [Google Scholar] [CrossRef]
  21. Tóth, E.G.; Tremblay, F.; Housset, J.M.; Bergeron, Y.; Carcaillet, C. Geographic isolation and climatic variability contribute to genetic differentiation in fragmented populations of the long-lived subalpine conifer Pinus cembra L. in the western Alps. BMC Evol. Biol. 2019, 19, 190. [Google Scholar] [CrossRef] [Green Version]
  22. Zięba, A.; Różański, W.; Bukowski, M.; Pałka, B.; Szwagrzyk, J. Distribution and habitat conditions of Pinus cembra forests in the Tatra Mountains. Dendrobiology 2019, 81, 86–96. [Google Scholar] [CrossRef] [Green Version]
  23. Carrer, M.; Unterholzner, L.; Castagneri, D. Wood anatomical traits highlight complex temperature influence on Pinus cembra at high elevation in the Eastern Alps. Int. J. Biometeorol. 2018, 62, 1745–1753. [Google Scholar] [CrossRef] [PubMed]
  24. Carrer, M.; Urbinati, C. Age-dependent tree-ring growth responses to climate in Larix decidua and Pinus cembra. Ecology 2004, 85, 730–740. [Google Scholar] [CrossRef]
  25. Oberhuber, W.; Kofler, W.; Pfeifer, K.; Seeber, A.; Gruber, A.; Wieser, G. Long-term changes in tree-ring–climate relationships at Mt. Patscherkofel (Tyrol, Austria) since the mid-1980s. Trees 2008, 22, 31–40. [Google Scholar] [CrossRef] [Green Version]
  26. Saulnier, M.; Edouard, J.L.; Corona, C.; Guibal, F. Climate/growth relationships in a Pinus cembra high-elevation network in the Southern French Alps. Ann. For. Sci. 2011, 68, 189–200. [Google Scholar] [CrossRef] [Green Version]
  27. Popa, I.; Nechita, C.; Hofgaard, A. Stand structure, recruitment and growth dynamics in mixed subalpine spruce and Swiss stone pine forests in the Eastern Carpathians. Sci. Total Environ. 2017, 598, 1050–1057. [Google Scholar] [CrossRef]
  28. Popa, I.; Kern, Z. Long-term summer temperature reconstruction inferred from tree-ring records from the Eastern Carpathians. Clim. Dyn. 2009, 32, 1107–1117. [Google Scholar] [CrossRef]
  29. Roibu, C.C.; Popa, I.; Kirchhefer, A.J.; Palaghianu, C. Growth responses to climate in a tree-ring network of European beech (Fagus sylvatica L.) from the eastern limit of its natural distribution area. Dendrochronologia 2017, 42, 104–116. [Google Scholar] [CrossRef]
  30. Rozas, V. Dendrochronology of pedunculate oak (Quercus robur L.) in an old-growth pollarded woodland in northern Spain: Tree-ring growth responses to climate. Ann. For. Sci. 2005, 62, 209–218. [Google Scholar] [CrossRef] [Green Version]
  31. Jevšenak, J.; Levanič, T. dendroTools: R package for studying linear and nonlinear responses between tree-rings and daily environmental data. Dendrochronologia 2018, 48, 32–39. [Google Scholar] [CrossRef] [Green Version]
  32. Jevšenak, J. Daily climate data reveal stronger climate-growth relationships for an extended European tree-ring network. Quat. Sci. Rev. 2019, 221, 105868. [Google Scholar] [CrossRef]
  33. Vaganov, E.A.; Hughes, M.K.; Shashkin, A.V. Growth dynamics of conifer tree rings: Images of past and future environments. In Ecological Study; Springer Nature: Berlin/Heidelberg, Germany; New York, NY, USA, 2006; Volume 183, p. 350. [Google Scholar]
  34. Niedzwiedz, T. Climate of the Tatra Mountains. Mt. Res. Dev. 1992, 12, 131–146. [Google Scholar] [CrossRef]
  35. Caudullo, G.; Welk, E.; San-Miguel-Ayanz, J. Chorological maps for the main European woody species. Data Brief 2017, 12, 662–666. [Google Scholar] [CrossRef] [PubMed]
  36. Grissino-Mayer, H.D. Evaluating crossdating accuracy: A manual and tutorial for the computer program COFECHA. Tree-Ring Res. 2001, 57, 5–21. Available online: http://hdl.handle.net/10150/251654 (accessed on 21 April 2023).
  37. Holmes, R.L. Computer-assisted quality control in tree-ring dating and measurement. Tree-Ring Bull. 1983, 43, 69–75. [Google Scholar]
  38. Cornes, R.C.; van der Schrier, G.; van den Besselaar, E.J.; Jones, P.D. An ensemble version of the E-OBS temperature and precipitation data sets. J. Geophys. Res. Atmos. 2018, 123, 9391–9409. [Google Scholar] [CrossRef] [Green Version]
  39. Bunn, A.G. Statistical and visual crossdating in R using the dplR library. Dendrochronologia 2010, 28, 251–258. [Google Scholar] [CrossRef]
  40. R Development Core Team. R: A Language and Environment for Statistical Computing. Available online: https://www.r-project.org (accessed on 21 April 2023).
  41. McCarroll, D.; Loader, N.J. Stable isotopes in tree rings. Quat. Sci. Rev. 2004, 23, 771–801. [Google Scholar] [CrossRef]
  42. Fritts, H.C. Tree Rings and Climate; Academic Press: London, UK, 1976; p. 582. [Google Scholar]
  43. Bunn, A.G. A dendrochronology program library in R (dplR). Dendrochronologia 2008, 26, 115–124. [Google Scholar] [CrossRef]
  44. Buras, A. A comment on the expressed population signal. Dendrochronologia 2017, 44, 130–132. [Google Scholar] [CrossRef]
  45. Wigley, T.M.L.; Briffa, K.R.; Jones, P.D. On the average value of correlated time series, with applications in dendroclimatology and hydrometeorology. J. Appl. Meteorol. Climatol. 1984, 23, 201–213. [Google Scholar] [CrossRef]
  46. Bednarz, Z. Relationship of Tree-Ring Widths in the Tatra Mountains to Variations in Monthly Temperature and Precipitation; Mitteilungen der Forstlichen Bundes-Versuchsanstalt: Wien, Austria, 1981; Volume 142, pp. 367–389. [Google Scholar]
  47. Büntgen, U.; Trnka, M.; Krusic, P.J.; Kyncl, T.; Kyncl, J.; Luterbacher, J.; Zorita, E.; Ljungqvist, F.C.; Auer, I.; Konter, O.; et al. Tree-ring amplification of the early nineteenth-century summer cooling in Central Europe. J. Clim. 2015, 28, 5272–5288. [Google Scholar] [CrossRef] [Green Version]
  48. Știrbu, M.I.; Roibu, C.C.; Carrer, M.; Mursa, A.; Unterholzner, L.; Prendin, A.L. Contrasting climate sensitivity of Pinus cembra tree-ring traits in the Carpathians. Front. Plant Sci. 2022, 13, 855003. [Google Scholar] [CrossRef]
  49. Körner, C.; Hoch, G. Not every high-latitude or high-elevation forest edge is a treeline. J. Biogeogr. 2023, 50, 838–845. [Google Scholar] [CrossRef]
  50. Carrer, M.; Nola, P.; Eduard, J.L.; Motta, R.; Urbinati, C. Regional variability of climate–growth relationships in Pinus cembra high elevation forests in the Alps. J. Ecol. 2007, 95, 1072–1083. [Google Scholar] [CrossRef]
  51. Housset, J.M.; Tóth, E.G.; Girardin, M.P.; Tremblay, F.; Motta, R.; Bergeron, Y.; Carcaillet, C. Tree-rings, genetics and the environment: Complex interactions at the rear edge of species distribution range. Dendrochronologia 2021, 69, 125863. [Google Scholar] [CrossRef]
  52. Vittoz, P.; Rulence, B.; Largey, T.; Freléchoux, F. Effects of climate and land-use change on the establishment and growth of cembran pine (Pinus cembra L.) over the altitudinal treeline ecotone in the Central Swiss Alps. Arct. Antarct. Alp. Res. 2008, 40, 225–232. [Google Scholar] [CrossRef] [Green Version]
  53. Mayr, S.; Hacke, U.; Schmid, P.; Schwienbacher, F.; Gruber, A. Frost drought in conifers at the alpine timberline: Xylem dysfunction and adaptations. Ecology 2006, 87, 3175–3185. [Google Scholar] [CrossRef] [Green Version]
  54. Oberhuber, W. Influence of climate on radial growth of Pinus cembra within the alpine timberline ecotone. Tree Physiol. 2004, 24, 291–301. [Google Scholar] [CrossRef]
  55. Simard, S.; Giovannelli, A.; Treydte, K.; Traversi, M.L.; King, G.M.; Frank, D.; Fonti, P. Intra-annual dynamics of non-structural carbohydrates in the cambium of mature conifer trees reflects radial growth demands. Tree Physiol. 2013, 33, 913–923. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  56. Körner, C.; Hoch, G. A test of treeline theory on a montane permafrost island. Arct. Antarct. Alp. Res. 2006, 38, 113–119. [Google Scholar] [CrossRef] [Green Version]
  57. Briffa, K.R.; Schweingruber, F.H.; Jones, P.D.; Osborne, T.J.; Shiyatov, S.G.; Vaganov, E.A. Reduced sensitivity of recent tree-growth to temperature at high northern latitudes. Nature 1998, 391, 678–682. [Google Scholar] [CrossRef]
  58. Paulsen, J.; Weber, U.M.; Körner, C. Tree growth near treeline: Abrupt or gradual reduction with altitude? Arct. Antarct. Alp. Res. 2000, 32, 14–20. [Google Scholar] [CrossRef]
  59. Körner, C. The cold range limit of trees. Trends Ecol. Evol. 2021, 36, 979–989. [Google Scholar] [CrossRef]
  60. Dzialuk, A.; Chybicki, I.; Gout, R.; Mączka, T.; Fleischer, P.; Konrad, H.; Curtu, L.; Sofletea, N.; Valadon, A. No reduction in genetic diversity of Swiss stone pine (Pinus cembra L.) in Tatra Mountains despite high fragmentation and small population size. Conserv. Genet. 2014, 15, 1433–1445. [Google Scholar] [CrossRef] [Green Version]
  61. Gugerli, F.; Brodbeck, S.; Lendvay, B.; Dauphin, B.; Bagnoli, F.; van der Knaap, W.O.; Tinner, W.; Höhn, M.; Vendramin, G.G.; Morales-Molino, C.; et al. A range-wide postglacial history of Swiss stone pine based on molecular markers and palaeoecological evidence. J. Biogeogr. 2023, 50, 1049–1062. [Google Scholar] [CrossRef]
  62. Zwijacz-Kozica, T.; Żywiec, M. Fifty-year changes in a strictly protected stone pine population in the Tatra National Park. Nat. Conserv. 2007, 64, 73–82. [Google Scholar]
Forests 14 01411 g001 550
Figure 1. Map showing study site location (yellow dot) and the distribution of Pinus cembra in the Carpathian Mountains (blue areas) [35].
Figure 1. Map showing study site location (yellow dot) and the distribution of Pinus cembra in the Carpathian Mountains (blue areas) [35].
Forests 14 01411 g001
Forests 14 01411 g002a 550Forests 14 01411 g002b 550
Figure 2. Climatic diagrams for the analysed period (1921–2009) and two subperiods (1921–1965 and 1966–2009) based on daily data for the study area: (a) Eleven-day running means of the daily mean, maximum, and minimum temperature; and (b) eleven-day running means of the daily sums of precipitation.
Figure 2. Climatic diagrams for the analysed period (1921–2009) and two subperiods (1921–1965 and 1966–2009) based on daily data for the study area: (a) Eleven-day running means of the daily mean, maximum, and minimum temperature; and (b) eleven-day running means of the daily sums of precipitation.
Forests 14 01411 g002aForests 14 01411 g002b
Forests 14 01411 g003 550
Figure 3. The TRWI chronology (solid line) and sample depth (dotted line) for 1921–2009 period.
Figure 3. The TRWI chronology (solid line) and sample depth (dotted line) for 1921–2009 period.
Forests 14 01411 g003
Forests 14 01411 g004 550
Figure 4. Correlations between the mean daily temperature and the TRWI chronology for the analysed periods. The colours show a significant (p < 0.05) correlation coefficient for consecutive window widths. The given values show the beginning of the specific time window.
Figure 4. Correlations between the mean daily temperature and the TRWI chronology for the analysed periods. The colours show a significant (p < 0.05) correlation coefficient for consecutive window widths. The given values show the beginning of the specific time window.
Forests 14 01411 g004
Forests 14 01411 g005 550
Figure 5. Correlations between the minimum daily temperature and the TRWI chronology for the analysed periods. The colours show a significant (p < 0.05) correlation coefficient for consecutive window widths. The given values show the beginning of the specific time window.
Figure 5. Correlations between the minimum daily temperature and the TRWI chronology for the analysed periods. The colours show a significant (p < 0.05) correlation coefficient for consecutive window widths. The given values show the beginning of the specific time window.
Forests 14 01411 g005
Forests 14 01411 g006 550
Figure 6. Correlations between the maximum daily temperature and the TRWI chronology for the analysed periods. The colours show a significant (p < 0.05) correlation coefficient for consecutive window widths. The given values show the beginning of the specific time window.
Figure 6. Correlations between the maximum daily temperature and the TRWI chronology for the analysed periods. The colours show a significant (p < 0.05) correlation coefficient for consecutive window widths. The given values show the beginning of the specific time window.
Forests 14 01411 g006
Forests 14 01411 g007 550
Figure 7. Correlations between daily precipitation and the TRWI chronology for the analysed periods. The colours show a significant (p < 0.05) correlation coefficient for consecutive window widths. The given values show the beginning of the specific time window.
Figure 7. Correlations between daily precipitation and the TRWI chronology for the analysed periods. The colours show a significant (p < 0.05) correlation coefficient for consecutive window widths. The given values show the beginning of the specific time window.
Forests 14 01411 g007
Table
Table 1. Statistics of the detrended chronology for the analysed period (1921–2009) and two subperiods (1921–1965 and 1966–2009).
Table 1. Statistics of the detrended chronology for the analysed period (1921–2009) and two subperiods (1921–1965 and 1966–2009).
ParameterNumber of YearsNumber of TreesInterseries Correlation (Rbar)Expressed Population Signal (EPS)Subsample Signal Strength (SSS)Mean Sensitivity (MS)
1921–2009891040.160.9510.9980.196
1921–1965451040.170.9530.9970.187
1966–2009441040.140.9420.9980.188
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Izworska, K.; Zielonka, T.; Matulewski, P.; Muter, E. Daily Climatic Data Better Explain the Radial Growth of Swiss Stone Pine (Pinus cembra L.) in High-Elevation Cliffs in the Carpathians. Forests 2023, 14, 1411. https://doi.org/10.3390/f14071411

AMA Style

Izworska K, Zielonka T, Matulewski P, Muter E. Daily Climatic Data Better Explain the Radial Growth of Swiss Stone Pine (Pinus cembra L.) in High-Elevation Cliffs in the Carpathians. Forests. 2023; 14(7):1411. https://doi.org/10.3390/f14071411

Chicago/Turabian Style

Izworska, Katarzyna, Tomasz Zielonka, Paweł Matulewski, and Elżbieta Muter. 2023. "Daily Climatic Data Better Explain the Radial Growth of Swiss Stone Pine (Pinus cembra L.) in High-Elevation Cliffs in the Carpathians" Forests 14, no. 7: 1411. https://doi.org/10.3390/f14071411

APA Style

Izworska, K., Zielonka, T., Matulewski, P., & Muter, E. (2023). Daily Climatic Data Better Explain the Radial Growth of Swiss Stone Pine (Pinus cembra L.) in High-Elevation Cliffs in the Carpathians. Forests, 14(7), 1411. https://doi.org/10.3390/f14071411

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop