Large-Scale Mapping of Carbon Stocks in Riparian Forests with Self-Organizing Maps and the k-Nearest-Neighbor Algorithm
Abstract
:1. Introduction
- (1)
- to create distribution maps of vegetation, soil, and total Corg stocks in a riparian forest, based on SOM and kNN algorithms and compare the results;
- (2)
- to compare and evaluate results with previous estimation techniques;
- (3)
- to evaluate the influence of additional geodata on estimation quality.
2. Material and Methods
2.1. Study Area

2.2. Data
| Available geodata | Derived parameters | Abbreviations |
|---|---|---|
| RapidEye image (1 August 2009) | Blue channel (440–510 nm) Green channel (520–590 nm) Red channel (630–685 nm) Red edge channel (690–730 nm) Near infrared channel (760–850 nm) | B G R RE NIR |
| Digital elevation model | Elevation above river level | altitude |
| Ground water model | Ground water level | MGW |
| Topographic map 1:50,00 (ÖK 50) | Distance to river | distance |
| Corg ground survey data from 2008 and 2010 | Above ground carbon stocks Below ground carbon stocks Total carbon stocks | Corg_veg Corg_soil Corg_tot |
2.3. Self-Organizing Maps (SOM)
2.4. k-Nearest Neighbor (kNN)

2.5. Validation
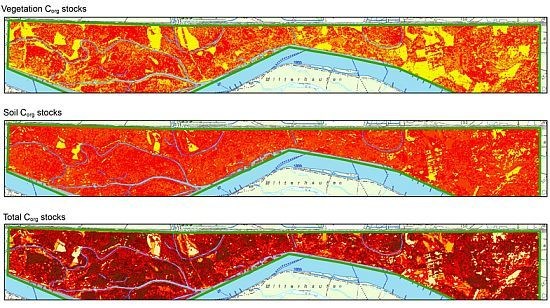
3. Results
3.1. Corg Stock Estimations


| Dataset | Approach | Vegetation Corg: Mg Corg in total study area (Mg C ha−1) | Soil Corg: Mg Corg in total study area (Mg C ha−1) | Total Corg: Mg Corg in total study area (Mg C ha−1) |
|---|---|---|---|---|
| RapidEye | SOM | 144043.49 (127.47) | 198390.17 (175.57) | 393735.41 (348.44) |
| kNN | 158791.28 (140.52) | 238362.66 (210.94) | 398114.52 (352.31) | |
| RapidEye + altitude + MGW + distance | SOM | 168056.05 (148.72) | 198635.46 (175.78) | 389228.63 (344.45) |
| kNN | 122856.37 (108.72) | 203001.62 (179.65) | 337092.95 (298.31) |
3.2. Error Estimates
| Dataset | Approach | Vegetation Corg stocks (average 149.65 Mg C ha−1) | Soil Corg stocks (average 192.1 Mg C ha−1) | Total Corg stocks (average 361.52 Mg C ha−1) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Bias | RMSE | % RMSE | Bias | RMSE | % RMSE | Bias | RMSE | % RMSE | ||
| RapidEye | SOM | −4.26 | 229.12 | 146.99 | 3.01 | 113.26 | 58.99 | −7.08 | 262.98 | 70.85 |
| kNN | 39.52 | 177.45 | 158.32 | 18.22 | 85.34 | 48.27 | 73.92 | 210.45 | 72.52 | |
| RapidEye + altitude + MGW + distance | SOM | 11.41 | 198.85 | 143.29 | 0.28 | 108.22 | 56.42 | 3.15 | 226.18 | 63.11 |
| kNN | −0.94 | 182.15 | 118.46 | −4.28 | 81.26 | 40.79 | −8.23 | 196.66 | 52.67 | |

4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Breijo, E.G.; Pinatti, C.O.; Peris, R.M.; Fillol, M.A.; Martinez-Manez, R.; Camino, J.S. Tnt detection using a voltammetric electronic tongue based on neural networks. Sens. Actuator A-Phys. 2013, 192, 1–8. [Google Scholar]
- Wang, Z.S.; Bian, S.R.; Liu, Y.; Liu, Z.H. The load characteristics classification and synthesis of substations in large area power grid. Int. J. Electr. Power Energy Syst. 2013, 48, 71–82. [Google Scholar]
- Xuan, S.Y.; Wu, Y.B.; Chen, X.F.; Liu, J.; Yan, A.X. Prediction of bioactivity of hiv-1 integrase st inhibitors by multilinear regression analysis and support vector machine. Bioorg. Med. Chem. Lett. 2013, 23, 1648–1655. [Google Scholar]
- Kanevski, M.; Timonin, V.; Pozdnukhov, A. Machine Learning Algorithms for Spatial Data Analysis and Modelling; EFPL Press: Lausanne, Switzerland, 2009; p. 377. [Google Scholar]
- Tomppo, E. Satellite image-based national forest inventory of finland. Int. Arch. Photogramm. Remote Sens. 1991, 28, 419–424. [Google Scholar]
- Tomppo, E.; Halme, M. Using coarse scale forest variables as ancillary information and weighting of variables in k-NN estimation: A genetic algorithm approach. Remote Sens. Environ. 2004, 92, 1–20. [Google Scholar] [CrossRef]
- Tomppo, E.; Goulding, C.; Katila, M. Adapting finnish multi-source forest inventory techniques to the new zealand preharvest inventory. Scand. J. For. Res. 1999, 14, 182–192. [Google Scholar]
- Koukal, T.; Suppan, F.; Schneider, W. The impact of relative radiometric calibration on the accuracy of knn-predictions of forest attributes. Remote Sens. Environ. 2007, 110, 431–437. [Google Scholar]
- McInerney, D.O.; Nieuwenhuis, M. A comparative analysis of knn and decision tree methods for the irish national forest inventory. Int. J. Remote Sens. 2009, 30, 4937–4955. [Google Scholar] [CrossRef]
- Fuchs, H.; Magdon, P.; Kleinn, C.; Flessa, H. Estimating aboveground carbon in a catchment of the siberian forest tundra: Combining satellite imagery and field inventory. Remote Sens. Environ. 2009, 113, 518–531. [Google Scholar] [CrossRef]
- Magnussen, S.; McRoberts, R.E.; Tomppo, E.O. Model-based mean square error estimators for k-nearest neighbour predictions and applications using remotely sensed data for forest inventories. Remote Sens. Environ. 2009, 113, 476–488. [Google Scholar]
- Stümer, W.; Kenter, B.; Köhl, M. Spatial interpolation of in situ data by self-organizing map algorithms (neural networks) for the assessment of carbon stocks in european forests. For. Ecol. Manag. 2010, 260, 287–293. [Google Scholar] [CrossRef]
- Lek, S.; Guégan, J.F. Artificial neural networks as a tool in ecological modelling, an introduction. Ecol. Modell. 1999, 120, 65–73. [Google Scholar]
- Astel, A.; Tsakovski, S.; Barbieri, P.; Simeonov, V. Comparison of self-organizing maps classification approach with cluster and principal components analysis for large environmental data sets. Water Res. 2007, 41, 4566–4578. [Google Scholar] [CrossRef]
- Shanmuganathan, S.; Sallis, P.; Buckeridge, J. Self-organising map methods in integrated modelling of environmental and economic systems. Environ. Modell. Softw. 2006, 21, 1247–1256. [Google Scholar] [CrossRef]
- Arribas-Bel, D.; Nijkamp, P.; Scholten, H. Multidimensional urban sprawl in europe: A self-organizing map approach. Comput. Environ. Urban Syst. 2011, 35, 263–275. [Google Scholar]
- Adamczyk, J.J.; Kurzac, M.; Park, Y.S.; Kruk, A. Application of a kohonen’s self-organizing map for evaluation of long-term changes in forest vegetation. J. Veg. Sci. 2013, 24, 405–414. [Google Scholar] [CrossRef]
- Giraudel, J.L.; Lek, S. A comparison of self-organizing map algorithm and some conventional statistical methods for ecological community ordination. Ecol. Modell. 2001, 146, 329–339. [Google Scholar] [CrossRef]
- Li, Q.; Yue, T.; Wang, C.; Zhang, W.; Yu, Y.; Li, B.; Yang, J.; Bai, G. Spatially distributed modeling of soil organic matter across China: An application of artificial neural network approach. Catena 2013, 104, 210–218. [Google Scholar]
- Hoffmann, T.; Glatzel, S.; Dikau, R. A carbon storage perspective on alluvial sediment storage in the rhine catchment. Geomorphology 2009, 108, 127–137. [Google Scholar] [CrossRef]
- Anonymous. IPCC Special Report on Land Use, Land-Use Change and Forestry; Cambridge University Press: Cambridge, UK, 2000; p. 24. [Google Scholar]
- Mitra, S.; Wassmann, R.; Vlek, P.L.G. An appraisal of global wetland area and its organic carbon stock. Anglais 2005, 88, 25–35. [Google Scholar]
- Cierjacks, A.; Kleinschmit, B.; Kowarik, I.; Graf, M.; Lang, F. Organic matter distribution in floodplain can be predicted using spatial and vegetation structure data. River Res. Appl. 2011, 27, 1048–1057. [Google Scholar] [CrossRef]
- Baritz, R.; Seufert, G.; Montanarella, L.; van Ranst, E. Carbon concentrations and stocks in forest soils of europe. For. Ecol. Manag. 2010, 260, 262–277. [Google Scholar] [CrossRef]
- Harrison, A.F.; Howard, P.J.A.; Howard, D.M.; Howard, D.C.; Hornung, M. Carbon storage in forest soils. Forestry 1995, 68, 335–348. [Google Scholar]
- Hofmann, G.; Anders, S. Waldökosysteme als Quellen und Senken für Kohlenstoff-Fallstudie ostdeutsche Länder. Beitr. Forstwirtsch. Landsch. 1996, 30, 9–16. [Google Scholar]
- Kooch, Y.; Hosseini, S.M.; Zaccone, C.; Jalilvand, H.; Hojjati, S.M. Soil organic carbon sequestration as affected by afforestation: The darab kola forest (north of Iran) case study. J. Environ. Monit. 2012, 14, 2438–2446. [Google Scholar] [CrossRef]
- Lal, R. Forest soils and carbon sequestration. For. Ecol. Manag. 2005, 220, 242–258. [Google Scholar]
- 2006 IPCC Guidelines for National Greenhouse Gas Inventories. In National Greenhouse Gas Inventories Programme; Eggleston, H.S.; Buendia, L.; Miwa, K.; Ngara, T.; Tanabe, K. (Eds.) IPCC National Greenhouse Gas Inventories Programme Technical Support Unit: Hayama, Kanagawa, Japan, 2006.
- Beets, P.N.; Brandon, A.M.; Goulding, C.J.; Kimberley, M.O.; Paul, T.S.H.; Searles, N. The national inventory of carbon stock in New Zealand’s pre-1990 planted forest using a LiDAR incomplete-transect approach. For. Ecol. Manag. 2013, 280, 187–197. [Google Scholar]
- Smith, J.E.; Heath, L.S.; Hoover, C.M. Carbon factors and models for forest carbon estimates for the 2005–2011 National Greenhouse Gas Inventories of the United States. For. Ecol. Manag. 2013, 307, 7–19. [Google Scholar] [CrossRef]
- Olofsson, P.; Lagergren, F.; Lindroth, A.; Lindström, J.; Klemedtsson, L.; Kutsch, W.; Eklundh, L. Towards operational remote sensing of forest carbon balance across northern europe. Biogeosciences 2008, 5, 817–832. [Google Scholar]
- Patenaude, G.; Milne, R.; Dawson, T.P. Synthesis of remote sensing approaches for forest carbon estimation: Reporting to the kyoto protocol. Environ. Sci. Policy 2005, 8, 161–178. [Google Scholar]
- Gallaun, H.; Zanchi, G.; Nabuurs, G.J.; Hengeveld, G.; Schardt, M.; Verkerk, P.J. EU-wide maps of growing stock and above-ground biomass in forests based on remote-sensing and field measurements. For. Ecol. Manag. 2010, 260, 252–261. [Google Scholar] [CrossRef]
- Suchenwirth, L.; Förster, M.; Cierjacks, A.; Lang, F.; Kleinschmit, B. Knowledge-based classification of remote sensing data for the estimation of below- and above-ground organic carbon stocks in riparian forests. Wetl. Ecol. Manag. 2012, 20, 151–163. [Google Scholar]
- Suchenwirth, L.; Förster, M.; Lang, F.; Kleinschmit, B. Estimation and mapping of carbon stocks in riparian forests by using a machine learning approach with multiple geodata. Photogramm. Fernerkund. Geoinforma. 2013, 4, 333–349. [Google Scholar]
- Güneralp, I.; Filippi, A.M.; Randall, J. Estimation of floodplain aboveground biomass using multispectral remote sensing and nonparametric modeling. Int. J. Appl. Earth Obs. Geoinforma. 2014, 33, 119–126. [Google Scholar] [CrossRef]
- Lair, G.J.; Zehetner, F.; Fiebig, M.; Gerzabek, M.H.; van Gestel, C.A.M.; Hein, T.; Hohensinner, S.; Hsu, P.; Jones, K.C.; Jordan, G.; et al. How do long-term development and periodical changes of river-floodplain systems affect the fate of contaminants? Results from european rivers. Environ. Pollut. 2009, 157, 3336–3346. [Google Scholar] [CrossRef]
- Wagner-Lücker, I.; Lanz, E.; Förster, M.; Janauer, G.A.; Reiter, K. Knowledge-based framework for delineation and classification of ephemeral plant communities in riverine landscapes to support ec habitat directive assessment. Ecol. Inf. 2013, 14, 44–47. [Google Scholar] [CrossRef]
- Zehetner, F.; Lair, G.J.; Gerzabek, M.H. Rapid carbon accretion and organic matter pool stabilization in riverine floodplain soils. Glob. Biogeochem. Cycles 2009, 23, GB4004. [Google Scholar]
- Cierjacks, A.; Kleinschmit, B.; Babinsky, M.; Kleinschroth, F.; Markert, A.; Menzel, M.; Ziechmann, U.; Schiller, T.; Graf, M.; Lang, F. Carbon stocks of soil and vegetation on danubian floodplains. J. Plant Nutr. Soil Sci. 2010, 173, 644–653. [Google Scholar] [CrossRef]
- Sandau, R. Status and trends of small satellite missions for earth observation. Acta Astronaut. 2010, 66, 1–12. [Google Scholar]
- Schuster, C.; Förster, M.; Kleinschmit, B. Testing the red edge channel for improving land-use classifications based on high-resolution multi-spectral satellite data. Int. J. Remote Sens. 2012, 33, 5583–5599. [Google Scholar] [CrossRef]
- Rieger, I.; Lang, F.; Kleinschmit, B.; Kowarik, I.; Cierjacks, A. Fine root and aboveground carbon stocks in riparian forests: The role of diking, environmental gradients and dominant tree species. Plant Soil 2013, 2, 1–13. [Google Scholar]
- Kohonen, T. Self-organized formation of topologically correct feature maps. Biol. Cybern. 1982, 43, 59–69. [Google Scholar] [CrossRef]
- Kohonen, T. Self-organizing Maps, 3rd ed.; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2001; Volume 30. [Google Scholar]
- Hall, P.; Park, B.U.; Samworth, R.J. Choice of neighbor order in nearest-neighbor classification. Ann. Stat. 2008, 20, 1236–1265. [Google Scholar]
- Kanevski, M.; Maignan, M. Analysis and Modelling of Spatial Environmental Data; EFPL Press: Lausanne, Switzerland, 2004; p. 288. [Google Scholar]
- Richter, K.; Atzberger, C.; Hank, T.B.; Mauser, W. Derivation of biophysical variables from earth observation data: Validation and statistical measures. J. Appl. Remote Sens. 2012, 6, 63557–63551. [Google Scholar]
- Hastie, T.; Tibshirani, R.; Friedman, J.H. The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd ed.; Springer: New York, NY, USA, 2009. [Google Scholar]
- Tuominen, S.; Pekkarinen, A. Performance of different spectral and textural aerial photograph features in multi-source forest inventory. Remote Sens. Environ. 2005, 94, 256–268. [Google Scholar] [CrossRef]
- Rocchini, D.; Foody, G.M.; Nagendra, H.; Ricotta, C.; Anand, M.; He, K.S.; Amici, V.; Kleinschmit, B.; Förster, M.; Schmidtlein, S.; et al. Uncertainty in ecosystem mapping by remote sensing. Comput. Geosci. 2013, 50, 128–135. [Google Scholar]
- Klobucar, D.; Subasic, M. Using self-organizing maps in the visualization and analysis of forest inventory. J. Biogeosci. For. 2012, 5, 216–223. [Google Scholar]
- Hsu, A.L.; Halgamuge, S.K. Enhancement of topology preservation and hierarchical dynamic self-organising maps for data visualisation. Int. J. Approx. Reason. 2003, 32, 259–279. [Google Scholar] [CrossRef]
- Goetz, S.; Baccini, A.; Laporte, N.; Johns, T.; Walker, W.; Kellndorfer, J.; Houghton, R.; Sun, M. Mapping and monitoring carbon stocks with satellite observations: A comparison of methods. Carbon Balanc. Manag. 2009, 4, 2. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Suchenwirth, L.; Stümer, W.; Schmidt, T.; Förster, M.; Kleinschmit, B. Large-Scale Mapping of Carbon Stocks in Riparian Forests with Self-Organizing Maps and the k-Nearest-Neighbor Algorithm. Forests 2014, 5, 1635-1652. https://doi.org/10.3390/f5071635
Suchenwirth L, Stümer W, Schmidt T, Förster M, Kleinschmit B. Large-Scale Mapping of Carbon Stocks in Riparian Forests with Self-Organizing Maps and the k-Nearest-Neighbor Algorithm. Forests. 2014; 5(7):1635-1652. https://doi.org/10.3390/f5071635
Chicago/Turabian StyleSuchenwirth, Leonhard, Wolfgang Stümer, Tobias Schmidt, Michael Förster, and Birgit Kleinschmit. 2014. "Large-Scale Mapping of Carbon Stocks in Riparian Forests with Self-Organizing Maps and the k-Nearest-Neighbor Algorithm" Forests 5, no. 7: 1635-1652. https://doi.org/10.3390/f5071635
APA StyleSuchenwirth, L., Stümer, W., Schmidt, T., Förster, M., & Kleinschmit, B. (2014). Large-Scale Mapping of Carbon Stocks in Riparian Forests with Self-Organizing Maps and the k-Nearest-Neighbor Algorithm. Forests, 5(7), 1635-1652. https://doi.org/10.3390/f5071635