Subset Analysis for Screening Drug–Drug Interaction Signal Using Pharmacovigilance Database
Abstract
:1. Introduction
- 1.
- The subset analysis used in this study detects signals from the target AE when the patient group using drug D1 takes drug D2. In all patient groups, when the signal value of the target AE is large for drug D2, the signal is detected regardless of whether the patient group is using drug D1.
- 2.
- Target AE signal intensities when a patient group using drug D1 takes drug D2 vs. that when a patient group using drug D2 takes drug D1 do not necessarily match. In other words, the value to be adopted as the target AE signal value when drug D1 and drug D2 are used concomitantly has not been fixed (i.e., no clear detection criteria have been defined for detecting drug–drug interaction signals).
2. Materials and Methods
2.1. Data Sources
2.2. Definitions of Adverse Drug Events
2.3. “Hypothetical” True Data of Adverse Events for Comparative Verification
2.4. Statistical Models and Criteria
2.4.1. Subset Analysis
2.4.2. Ω Shrinkage Measure Model
2.5. Evaluation of Detection Models
2.5.1. Using Evaluations of Classification in Machine Learning
2.5.2. Cohen’s Kappa Coefficient
2.6. Analysis Software
3. Results
3.1. Evaluations of Classification in Machine Learning
3.2. Cohen’s Kappa Coefficient
4. Discussions
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Berlin, J.A.; Glasser, S.C.; Ellenberg, S.S. Adverse event detection in drug development: Recommendations and obligations beyond phase 3. Am. J. Public Health 2008, 98, 1366–1371. [Google Scholar] [CrossRef] [PubMed]
- Noguchi, Y.; Ueno, A.; Otsubo, M.; Katsuno, H.; Sugita, I.; Kanematsu, Y.; Yoshida, A.; Esaki, H.; Tachi, T.; Teramachi, H. A New Search Method Using Association Rule Mining for Drug-Drug Interaction Based on Spontaneous Report System. Front. Pharmacol. 2018, 9, 197. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Iyer, S.V.; Harpaz, R.; LePendu, P.; Bauer-Mehren, A.; Shah, N.H. Mining clinical text for signals of adverse drug-drug interactions. J. Am. Med. Inf. Assoc. 2013, 21, 353–362. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Suling, M.; Pigeot, I. Signal Detection and Monitoring Based on Longitudinal Healthcare Data. Pharmaceutics 2012, 4, 607–640. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Evans, S.J.; Waller, P.C.; Davis, S. Use of proportional reporting ratios (PRRs) for signal generation from spontaneous adverse drug reaction reports. Pharmacoepidemiol. Drug Saf. 2001, 10, 483–486. [Google Scholar] [CrossRef] [PubMed]
- Rothman, K.J.; Lanes, S.; Sacks, S.T. The reporting odds ratio and its advantages over the proportional reporting ratio. Pharmacoepidemiol. Drug Saf. 2004, 13, 519–523. [Google Scholar] [CrossRef]
- Bate, A.; Lindquist, M.; Edwards, I.R.; Olsson, S.; Orre, R.; Lansner, A.; De Freitas, R.M. A Bayesian neural network method for adverse drug reaction signal generation. Eur. J. Clin. Pharmacol. 1998, 54, 315–321. [Google Scholar] [CrossRef]
- DuMouchel, W. Bayesian Data Mining in Large Frequency Tables, with an Application to the FDA Spontaneous Reporting System. Am. Stat. 1999, 53, 177–190. [Google Scholar] [CrossRef]
- Vilar, S.; Friedman, C.; Hripcsak, G. Detection of drug-drug interactions through data mining studies using clinical sources, scientific literature and social media. Brief. Bioinform. 2018, 19, 863–877. [Google Scholar] [CrossRef] [Green Version]
- Noguchi, Y.; Tachi, T.; Teramachi, H. Review of Statistical Methodologies for Detecting Drug-Drug Interactions Using Spontaneous Reporting Systems. Front. Pharmacol. 2019, 10, 1319. [Google Scholar] [CrossRef]
- Nagashima, T.; Shirakawa, H.; Nakagawa, T.; Kaneko, S. Prevention of antipsychotic-induced hyperglycaemia by vitamin D: A data mining prediction followed by experimental exploration of the molecular mechanism. Sci. Rep. 2016, 6, 26375. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Uno, T.; Wada, K.; Hosomi, K.; Matsuda, S.; Ikura, M.M.; Takenaka, H.; Terakawa, N.; Oita, A.; Yokoyama, S.; Kawase, A.; et al. Drug interactions between tacrolimus and clotrimazole troche: A data mining approach followed by a pharmacokinetic study. Eur. J. Clin. Pharmacol. 2020, 76, 117–125. [Google Scholar] [CrossRef] [PubMed]
- Sanagawa, A.; Hotta, Y.; Kondo, M.; Nishikawa, R.; Tohkin, M.; Kimura, K. Tumor lysis syndrome associated with bortezomib: A post-hoc analysis after signal detection using the US Food and Drug Administration Adverse Event Reporting System. Anti-Cancer Drugs 2020, 31, 183–189. [Google Scholar] [CrossRef] [PubMed]
- Noguchi, Y.; Tachi, T.; Teramachi, H. Comparison of signal detection algorithms based on frequency statistical model for drug-drug interaction using spontaneous reporting systems. Pharm. Res. 2020, 37, 86. [Google Scholar] [CrossRef]
- Kubota, K.; Koide, D.; Hirai, T. Comparison of data mining methodologies using Japanese spontaneous reports. Pharmacoepidemiol. Drug Saf. 2004, 13, 387–394. [Google Scholar] [CrossRef]
- Norén, G.N.; Sundberg, R.; Bate, A.; Edwards, I.R. A statistical methodology for drug-drug interaction surveillance. Stat. Med. 2008, 27, 3057–3070. [Google Scholar] [CrossRef]
- Susuta, Y.; Takahashi, Y. Safety risk evaluation methodology in detecting the medicine concomitant use risk which might cause critical drug rash. Jpn. J. Pharmacoepidemiol. 2014, 19, 39–49. [Google Scholar] [CrossRef] [Green Version]
- Thakrar, B.T.; Grundschober, S.B.; Doessegger, L. Detecting signals of drug-drug interactions in a spontaneous reports database. Br. J. Clin. Pharmacol. 2007, 64, 489–495. [Google Scholar] [CrossRef] [Green Version]
- Gosho, M.; Maruo, K.; Tada, K.; Hirakawa, A. Utilization of chi-square statistics for screening adverse drug-drug interactions in spontaneous reporting systems. Eur. J. Clin. Pharmacol. 2017, 73779–73786. [Google Scholar] [CrossRef]
- Cheng, F.J.; Syu, F.K.; Lee, K.H.; Chen, F.C.; Wu, C.H.; Chen, C.C. Correlation between drug-drug interaction-induced Stevens-Johnson syndrome and related deaths in Taiwan. J. Food Drug Anal. 2016, 24, 427–432. [Google Scholar] [CrossRef] [Green Version]
- Noguchi, Y.; Takaoka, M.; Hayashi, T.; Tachi, T.; Teramachi, H. Antiepileptic combination therapy with Stevens-Johnson syndrome and toxic epidermal necrolysis: Analysis of a Japanese pharmacovigilance database. Epilepsia 2020. [Google Scholar] [CrossRef] [PubMed]
- Caster, O.; Aoki, Y.; Gattepaille, L.M.; Grundmark, B. Disproportionality Analysis for Pharmacovigilance Signal Detection in Small Databases or Subsets: Recommendations for Limiting False-Positive Associations. Drug Saf. 2020, 43, 479–487. [Google Scholar] [CrossRef] [PubMed] [Green Version]
| Target AE | Other AEs | Total | |
|---|---|---|---|
| Concomitant use of drug D1 and drug D2 | n111 | n110 | n11+ |
| only drug D1 | n101 | n100 | n10+ |
| only drug D2 | n011 | n010 | n01+ |
| Neither drug D1 or drug D2 | n001 | n000 | n00+ |
| Total | n++1 | n++0 | n+++ |
| “Hypothetical” True Data | |||
|---|---|---|---|
| AE | non-AEs | ||
| analysis model | signal | TP | FP |
| Non-signal | FN | TN | |
| Analysis Model | TP | FP | TN | FN |
|---|---|---|---|---|
| Previous subset analysis | 542 | 1251 | 1750 | 381 |
| Newly proposed subset analysis | 542 | 367 | 2634 | 381 |
| Ω shrinkage measure model | 538 | 174 | 2827 | 385 |
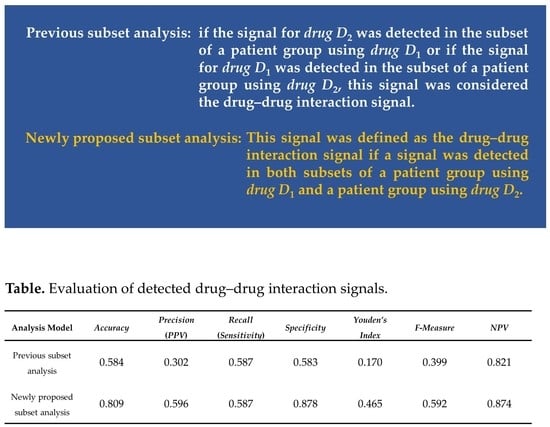
| Analysis Model | Accuracy | Precision(PPV) | Recall(Sensitivity) | Specificity | Youden’s Index | F-Measure | NPV |
| Previous subset analysis | 0.584 | 0.302 | 0.587 | 0.583 | 0.170 | 0.399 | 0.821 |
| Newly proposed subset analysis | 0.809 | 0.596 | 0.587 | 0.878 | 0.465 | 0.592 | 0.874 |
| Ω shrinkage measure model | 0.858 | 0.756 | 0.583 | 0.942 | 0.525 | 0.658 | 0.880 |
| Analysis Model | All Case | n111 ≥ 3 | ||||
|---|---|---|---|---|---|---|
| κ (95% CI) | Ppositive | Pnegative | κ (95% CI) | Ppositive | Pnegative | |
| Previous subset analysis | 0.088 (0.071–0.105) | 0.325 | 0.684 | −0.120 (−0.151–0.088) | 0.556 | 0.296 |
| Newly proposed subset analysis | 0.375 (0.355–0.395) | 0.502 | 0.870 | 0.355 (0.327–0.384) | 0.678 | 0.674 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Noguchi, Y.; Tachi, T.; Teramachi, H. Subset Analysis for Screening Drug–Drug Interaction Signal Using Pharmacovigilance Database. Pharmaceutics 2020, 12, 762. https://doi.org/10.3390/pharmaceutics12080762
Noguchi Y, Tachi T, Teramachi H. Subset Analysis for Screening Drug–Drug Interaction Signal Using Pharmacovigilance Database. Pharmaceutics. 2020; 12(8):762. https://doi.org/10.3390/pharmaceutics12080762
Chicago/Turabian StyleNoguchi, Yoshihiro, Tomoya Tachi, and Hitomi Teramachi. 2020. "Subset Analysis for Screening Drug–Drug Interaction Signal Using Pharmacovigilance Database" Pharmaceutics 12, no. 8: 762. https://doi.org/10.3390/pharmaceutics12080762
APA StyleNoguchi, Y., Tachi, T., & Teramachi, H. (2020). Subset Analysis for Screening Drug–Drug Interaction Signal Using Pharmacovigilance Database. Pharmaceutics, 12(8), 762. https://doi.org/10.3390/pharmaceutics12080762