Pharmacokinetic—Pharmacodynamic Modeling of Tumor Targeted Drug Delivery Using Nano-Engineered Mesenchymal Stem Cells
Abstract
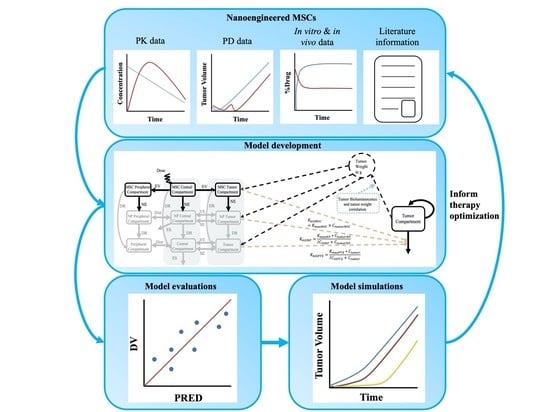
:1. Introduction
2. Materials and Methods
2.1. Data
2.1.1. PK Data
2.1.2. PD Data
2.2. PK–PD Modeling
2.2.1. PK Models
PK Model for PTX Solution (Bottom Layer)
PK Model for PTX -PLGA NPs (Middle Layer)
PK Model for Nano-MSCs (Top Layer)
Krel and Kexo Estimation
2.2.2. PK–PD Model
Correlation between Tumor Weight and Tumor Bioluminescence
2.3. Model Evaluations
2.4. PK and PK–PD Model Simulations
3. Results
3.1. PK and PD Data Exploration
3.2. In Vitro and In Vivo Kinetics Parameter Estimation
3.3. PK and PK–PD Model Parameters
3.4. Model Evaluations
| Parameters | Estimates (%RSE) | SIR Medians (95% CIs) | Units | Sources | Definitions |
|---|---|---|---|---|---|
| Model Associated Parameters | |||||
| PPTX | 0.0875 | cm/h | Literature [31,33] | Permeability rate constant for PTX free drug | |
| DPTX | 0.01 | cm2/h | Literature [31,33] | Diffusion rate constant for PTX free drug | |
| EPTX | 0.44 | unitless | Literature [31,33] | Tumor fraction accessible by PTX free drug | |
| Rkrogh | 0.0008 | cm | Assumed [41] | Inter-capillary distance | |
| Rcap | 0.0075 | cm | Assumed [42] | Radius of tumor-associated capillaries | |
| VT | 0.3 (PK); Dynamic (PD) | mL | Assumed (PK); Dynamic (PD) | Tumor volume | |
| Rtumor | 0.42 (PK); Dynamic (PD) | cm | Calculated/Assumed (PK); Dynamic (PD) | Tumor radius | |
| CLPTX | 0.909 (23%) | 0.952 (0.684, 1.305) | mL/h | Estimated | Clearance for PTX free drug |
| CLDPTX | 0.336 (68%) | 0.424 (0.193, 0.712) | mL/h | Estimated | Distribution clearance for PTX free drug |
| VPTXcentral | 6.64 (30%) | 7.06 (2.81, 11.49) | mL | Estimated | Central compartment volume of distribution for PTX free drug |
| VPTXperipheral | 18.5 (53%) | 22.6 (12.6, 35.7) | mL | Estimated | Peripheral compartment volume of distribution for PTX free drug |
| fuPTX | 0.0237 (46%) | 0.0237 (0.0119, 0.0499) | unitless | Estimated | Plasma to blood ratio for PTX free drug |
| PNP | 0.00035 | cm/h | Literature [43] | Permeability rate constant for PTX in the form of PLGA NPs | |
| DNP | 3.6 × 10−6 | cm2/h | Literature [44] | Diffusion rate constant for PTX in the form of PLGA NPs | |
| ENP | 0.055 | unitless | Literature [33] | Tumor fraction accessible by PTX in the form of PLGA NPs | |
| Krel | 0.0085 | 1/h | Calculated | First order drug release rate constant for PTX free drug from PTX-PLGA NPs | |
| CLNP | 0.241 (17%) | 0.259 (0.172, 0.340) | mL/h | Estimated | Clearance for PTX in the form of PLGA NPs |
| CLDNP | 0.0627 (48%) | 0.0681 (0.0349, 0.1244) | mL/h | Estimated | Distribution clearance for PTX in the form of PLGA NPs |
| VNPcentral | 1.32 (17%) | 1.41 (0.85, 1.96) | mL | Estimated | Central compartment volume of distribution for PTX in the form of PLGA NPs |
| VNPperipheral | 43.2 (141%) | 79.0 (16.6, 219.3) | mL | Estimated | Peripheral compartment volume of distribution for PTX in the form of PLGA NPs |
| fuNP | 0.00302 (57%) | 0.00325 (0.00127, 0.00684) | unitless | Estimated | Plasma to blood ratio for PTX in the form of PLGA NPs |
| Kexo | 0.081 | 1/h | Calculated | First order exocytosis rate constant for PTX-PLGA NPs from nano-MSCs | |
| Kct | 1.45 (22%) | 1.39 (1.04, 1.84) | 1/h | Estimated | Rate constant describing central to tumor compartment transfer for PTX in the form of nano-MSCs |
| Kcp | 10.2 (2%) | 10.2 (9.8, 10.8) | 1/h | Estimated | Rate constant describing central to peripheral compartment transfer for PTX in the form of nano-MSCs |
| VMSCcentral | 7.15 × 10−8 (30%) | 8.50 × 10−8 (2.22 × 10−8, 1.94 × 10−7) | mL | Estimated | Central compartment volume of distribution for PTX in the form of nano-MSCs |
| VMSCperipheral | 15021 (55%) | 13565 (932, 33,564) | mL | Estimated | Peripheral compartment volume of distribution for PTX in the form of nano-MSCs |
| Residual Unexplained Variability (RUV, proportional, CV%) | |||||
| εPTX_plasma | 116% (20%) | 118.5% (67.7%, 176.6%) | Estimated | RUV for PTX solution plasma PK profiles | |
| εPTX_tumor | 64.9% (25%) | 71.5% (46.4%, 103.9%) | Estimated | RUV for PTX solution lung PK profiles | |
| εNP_plasma | 81.2% (71%) | 100.8% (50.0%, 167.6%) | Estimated | RUV for PTX-PLGA NPs plasma PK profiles | |
| εNP_tumor | 54.5% (14%) | 58.8% (42.7%, 74.0%) | Estimated | RUV for PTX-PLGA NPs lung PK profiles | |
| εMSC_plasma | 87.3% (26%) | 86.4% (73.4%, 118.5%) | Estimated | RUV for nano-MSCs plasma PK profiles | |
| εMSC_tumor | 58.1% (22%) | 61.2% (43.4%, 85.7%) | Estimated | RUV for nano-MSCs lung PK profiles | |
| Parameters | Estimates (%RSE) | SIR Medians (95% CIs) | Units | Sources | Definitions |
|---|---|---|---|---|---|
| Model Associated Parameters | |||||
| Kg0CTR | 0.00339 (6%) | 0.00339 (0.00325, 0.00352) | /h | Estimated | First order tumor growth rate constant for animals receiving no treatments |
| Kg0PTX | 0.00372 (9%) | 0.00367 (0.00338, 0.00397) | /h | Estimated | First order tumor growth rate constant for animals receiving PTX solution |
| Kg0PTXNP | 0.00417(5%) | 0.00418 (0.00394, 0.00445) | /h | Estimated | First order tumor growth rate constant for animals receiving PTX-PLGA NPs |
| Kg0MSC | 0.00588 (11%) | 0.00585 (0.00528, 0.00639) | /h | Estimated | First order tumor growth rate constant for animals receiving nano-MSCs |
| TVBLCTR | 0.360 (16%) | 0.365 (0.251, 0.488) | 106 photon/s | Estimated | Baseline tumor bioluminescence for animals receiving no treatments |
| TVBLPTX | 0.376 (43%) | 0.387 (0.208, 0.593) | 106 photon/s | Estimated | Baseline tumor bioluminescence for animals receiving PTX solution |
| TVBLPTXNP | 0.539 (18%) | 0.549 (0.365, 0.730) | 106 photon/s | Estimated | Baseline tumor bioluminescence for animals receiving PTX-PLGA NPs |
| TVBLMSC | 0.227 (14%) | 0.232 (0.173, 0.287) | 106 photon/s | Estimated | Baseline tumor bioluminescence for animals receiving nano-MSCs |
| KmaxPTX | 0.00343 (26%) | 0.00332 (0.00261, 0.00398) | /h | Estimated | Maximal tumor killing rate induced by PTX free drug |
| KmaxNP | 0.000427 (372%) | 0.000755 (0.000035, 0.002192) | /h | Estimated | Maximal tumor killing rate induced by PTX in the form of PLGA NPs |
| KMSC | 4.35 × 10−6 (30%) | 4.31 × 10−6 (2.79 × 10−6, 5.75 × 10−6) | /(h*(ng/mL)) | Estimated | Linear tumor killing rate constant induced by PTX in the form of nano-MSCs |
| IC50PTX | 1.5 | ng/mL | Literature [16] | Concentration of PTX free drug can introduce 50% KmaxPTX | |
| IC50NP | 5.7 | ng/mL | Literature [16] | Concentration of PTX in the form of PLGA NPs can introduce 50% KmaxNP | |
| Between Subject Variability (BSV, proportional, CV%) | |||||
| ηTVBL | 96.4% (9%) | 99.1% (77.3%, 123.6%) | Shrinkage (0%) | Estimated | BSV on baseline tumor bioluminescence |
| Residual Unexplained Variability (RUV, CV%) | |||||
| εPTX_plasma | 49.3% (5%) | 49.5% (45.1%, 53.7%) | Estimated | RUV for tumor bioluminescence profiles in animals receiving no treatments | |
| εPTX_tumor | 66.8% (7%) | 67.4% (59.1%, 76.6%) | Estimated | RUV for tumor bioluminescence profiles in animals receiving PTX solution | |
| εNP_plasma | 62.4% (8%) | 63.0% (54.9%, 71.2%) | Estimated | RUV for tumor bioluminescence profiles in animals receiving PTX–PLGA- NPs | |
| εNP_tumor | 62.2% (10%) | 63.0% (54.8%, 72.2%) | Estimated | RUV for tumor bioluminescence profiles in animals receiving nano-MSCs | |
3.5. Nano-MSC PK Model Simulation
3.6. PK–PD Model Simulation
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Afanasyev, B.; Elstner, E.; Zander, A.A.J. Friedenstein, founder of the mesenchymal stem cell concept. Cell. Ther. Transplant. 2009, 1, 35–38. [Google Scholar]
- Cheng, S.; Nethi, S.K.; Rathi, S.; Layek, B.; Prabha, S. Engineered Mesenchymal Stem Cells for Targeting Solid Tumors: Therapeutic Potential beyond Regenerative Therapy. J. Pharm. Exp. 2019, 370, 231–241. [Google Scholar] [CrossRef] [PubMed]
- Lin, W.; Xu, L.; Zwingenberger, S.; Gibon, E.; Goodman, S.B.; Li, G. Mesenchymal stem cells homing to improve bone healing. J. Orthop. Transl. 2017, 9, 19–27. [Google Scholar] [CrossRef] [PubMed]
- Thakker, R.; Yang, P. Mesenchymal stem cell therapy for cardiac repair. Curr. Treat. Options Cardiovasc. Med. 2014, 16, 323. [Google Scholar] [CrossRef] [Green Version]
- Fitzsimmons, R.E.B.; Mazurek, M.S.; Soos, A.; Simmons, C.A. Mesenchymal Stromal/Stem Cells in Regenerative Medicine and Tissue Engineering. Stem Cells Int. 2018, 2018, 8031718. [Google Scholar] [CrossRef]
- Park, J.S.; Suryaprakash, S.; Lao, Y.H.; Leong, K.W. Engineering mesenchymal stem cells for regenerative medicine and drug delivery. Methods 2015, 84, 3–16. [Google Scholar] [CrossRef] [Green Version]
- Kadiyala, S.; Young, R.G.; Thiede, M.A.; Bruder, S.P. Culture expanded canine mesenchymal stem cells possess osteochondrogenic potential in vivo and in vitro. Cell Transpl. 1997, 6, 125–134. [Google Scholar] [CrossRef]
- Morandi, F.; Raffaghello, L.; Bianchi, G.; Meloni, F.; Salis, A.; Millo, E.; Ferrone, S.; Barnaba, V.; Pistoia, V. Immunogenicity of human mesenchymal stem cells in HLA-class I-restricted T-cell responses against viral or tumor-associated antigens. Stem Cells 2008, 26, 1275–1287. [Google Scholar] [CrossRef] [Green Version]
- Schu, S.; Nosov, M.; O’Flynn, L.; Shaw, G.; Treacy, O.; Barry, F.; Murphy, M.; O’Brien, T.; Ritter, T. Immunogenicity of allogeneic mesenchymal stem cells. J. Cell Mol. Med. 2012, 16, 2094–2103. [Google Scholar] [CrossRef]
- Wang, M.; Yuan, Q.; Xie, L. Mesenchymal Stem Cell-Based Immunomodulation: Properties and Clinical Application. Stem Cells Int. 2018, 2018, 3057624. [Google Scholar] [CrossRef]
- Sun, Z.; Wang, S.; Zhao, R.C. The roles of mesenchymal stem cells in tumor inflammatory microenvironment. J. Hematol. Oncol. 2014, 7, 14. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rhodes, L.V.; Antoon, J.W.; Muir, S.E.; Elliott, S.; Beckman, B.S.; Burow, M.E. Effects of human mesenchymal stem cells on ER-positive human breast carcinoma cells mediated through ER-SDF-1/CXCR4 crosstalk. Mol. Cancer 2010, 9, 295. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhao, Y.; Tang, S.; Guo, J.; Alahdal, M.; Cao, S.; Yang, Z.; Zhang, F.; Shen, Y.; Sun, M.; Mo, R.; et al. Targeted delivery of doxorubicin by nano-loaded mesenchymal stem cells for lung melanoma metastases therapy. Sci. Rep. 2017, 7, 44758. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, X.; Yao, S.; Liu, C.; Jiang, Y. Tumor tropic delivery of doxorubicin-polymer conjugates using mesenchymal stem cells for glioma therapy. Biomaterials 2015, 39, 269–281. [Google Scholar] [CrossRef]
- Layek, B.; Sadhukha, T.; Panyam, J.; Prabha, S. Nano-Engineered Mesenchymal Stem Cells Increase Therapeutic Efficacy of Anticancer Drug Through True Active Tumor Targeting. Mol. Cancer 2018, 17, 1196–1206. [Google Scholar] [CrossRef] [Green Version]
- Sadhukha, T.; O’Brien, T.D.; Prabha, S. Nano-engineered mesenchymal stem cells as targeted therapeutic carriers. J. Control Release 2014, 196, 243–251. [Google Scholar] [CrossRef]
- Chen, X.; Lin, X.; Zhao, J.; Shi, W.; Zhang, H.; Wang, Y.; Kan, B.; Du, L.; Wang, B.; Wei, Y.; et al. A tumor-selective biotherapy with prolonged impact on established metastases based on cytokine gene-engineered MSCs. Mol. Ther. 2008, 16, 749–756. [Google Scholar] [CrossRef]
- Yang, X.; Du, J.; Xu, X.; Xu, C.; Song, W. IFN-gamma-secreting-mesenchymal stem cells exert an antitumor effect in vivo via the TRAIL pathway. J. Immunol. Res. 2014, 2014, 318098. [Google Scholar] [CrossRef] [Green Version]
- Relation, T.; Yi, T.; Guess, A.J.; La Perle, K.; Otsuru, S.; Hasgur, S.; Dominici, M.; Breuer, C.; Horwitz, E.M. Intratumoral Delivery of Interferongamma-Secreting Mesenchymal Stromal Cells Repolarizes Tumor-Associated Macrophages and Suppresses Neuroblastoma Proliferation In Vivo. Stem Cells 2018, 36, 915–924. [Google Scholar] [CrossRef] [Green Version]
- Dai, T.; Yang, E.; Sun, Y.; Zhang, L.; Zhang, L.; Shen, N.; Li, S.; Liu, L.; Xie, Y.; Wu, S.; et al. Preparation and drug release mechanism of CTS-TAX-NP-MSCs drug delivery system. Int. J. Pharm. 2013, 456, 186–194. [Google Scholar] [CrossRef]
- Benzekry, S. Artificial Intelligence and Mechanistic Modeling for Clinical Decision Making in Oncology. Clin. Pharm. 2020. [Google Scholar] [CrossRef] [PubMed]
- Agoram, B.M.; Martin, S.W.; van der Graaf, P.H. The role of mechanism-based Pharmacokinetic–Pharmacodynamic (PK–PD) modelling in translational research of biologics. Drug Discov. Today 2007, 12, 1018–1024. [Google Scholar] [CrossRef] [PubMed]
- Danhof, M.; de Lange, E.C.; Della Pasqua, O.E.; Ploeger, B.A.; Voskuyl, R.A. Mechanism-based Pharmacokinetic–Pharmacodynamic (PK–PD) modeling in translational drug research. Trends Pharm. Sci. 2008, 29, 186–191. [Google Scholar] [CrossRef] [PubMed]
- Wada, R.; Erickson, H.K.; Lewis Phillips, G.D.; Provenzano, C.A.; Leipold, D.D.; Mai, E.; Johnson, H.; Tibbitts, J. Mechanistic pharmacokinetic/pharmacodynamic modeling of in vivo tumor uptake, catabolism, and tumor response of trastuzumab maytansinoid conjugates. Cancer Chemother. Pharm. 2014, 74, 969–980. [Google Scholar] [CrossRef] [PubMed]
- Delavenne, X.; Ollier, E.; Basset, T.; Bertoletti, L.; Accassat, S.; Garcin, A.; Laporte, S.; Zufferey, P.; Mismetti, P. A semi-mechanistic absorption model to evaluate drug-drug interaction with dabigatran: Application with clarithromycin. Br. J. Clin. Pharm. 2013, 76, 107–113. [Google Scholar] [CrossRef] [Green Version]
- Salinger, D.H.; Endres, C.J.; Martin, D.A.; Gibbs, M.A. A semi-mechanistic model to characterize the pharmacokinetics and pharmacodynamics of brodalumab in healthy volunteers and subjects with psoriasis in a first-in-human single ascending dose study. Clin. Pharm. Drug Dev. 2014, 3, 276–283. [Google Scholar] [CrossRef]
- Liu, C.; Ayyar, V.S.; Zheng, X.; Chen, W.; Zheng, S.; Mody, H.; Wang, W.; Heald, D.; Singh, A.P.; Cao, Y. Model-Based Cellular Kinetic Analysis of Chimeric Antigen Receptor-T Cells in Humans. Clin. Pharm. 2020. [Google Scholar] [CrossRef]
- Singh, A.P.; Zheng, X.; Lin-Schmidt, X.; Chen, W.; Carpenter, T.J.; Zong, A.; Wang, W.; Heald, D.L. Development of a quantitative relationship between CAR-affinity, antigen abundance, tumor cell depletion and CAR-T cell expansion using a multiscale systems PK–PD model. MAbs 2020, 12, 1688616. [Google Scholar] [CrossRef] [Green Version]
- Ayyar, V.S.; DuBois, D.C.; Nakamura, T.; Almon, R.R.; Jusko, W.J. Modeling Corticosteroid Pharmacokinetics and Pharmacodynamics, Part II: Sex Differences in Methylprednisolone Pharmacokinetics and Corticosterone Suppression. J. Pharm. Exp. 2019, 370, 327–336. [Google Scholar] [CrossRef]
- Keizer, R.J.; van Benten, M.; Beijnen, J.H.; Schellens, J.H.; Huitema, A.D. Pirana and PCluster: A modeling environment and cluster infrastructure for NONMEM. Comput. Methods Programs Biomed. 2011, 101, 72–79. [Google Scholar] [CrossRef]
- Shah, D.K.; King, L.E.; Han, X.; Wentland, J.A.; Zhang, Y.; Lucas, J.; Haddish-Berhane, N.; Betts, A.; Leal, M. A priori prediction of tumor payload concentrations: Preclinical case study with an auristatin-based anti-5T4 antibody-drug conjugate. AAPS J. 2014, 16, 452–463. [Google Scholar] [CrossRef] [Green Version]
- Shah, D.K.; Haddish-Berhane, N.; Betts, A. Bench to bedside translation of antibody drug conjugates using a multiscale mechanistic PK/PD model: A case study with brentuximab-vedotin. J. Pharm. Pharm. 2012, 39, 643–659. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, M.M.; Wittrup, K.D. A modeling analysis of the effects of molecular size and binding affinity on tumor targeting. Mol. Cancer 2009, 8, 2861–2871. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Thurber, G.M.; Schmidt, M.M.; Wittrup, K.D. Antibody tumor penetration: Transport opposed by systemic and antigen-mediated clearance. Adv. Drug Deliv. Rev. 2008, 60, 1421–1434. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Thurber, G.M.; Schmidt, M.M.; Wittrup, K.D. Factors determining antibody distribution in tumors. Trends Pharm. Sci. 2008, 29, 57–61. [Google Scholar] [CrossRef] [Green Version]
- Layek, B.; Sadhukha, T.; Prabha, S. Glycoengineered mesenchymal stem cells as an enabling platform for two-step targeting of solid tumors. Biomaterials 2016, 88, 97–109. [Google Scholar] [CrossRef]
- Martin, E.C.; Aarons, L.; Yates, J.W. Accounting for dropout in xenografted tumour efficacy studies: Integrated endpoint analysis, reduced bias and better use of animals. Cancer Chemother. Pharm. 2016, 78, 131–141. [Google Scholar] [CrossRef] [Green Version]
- Dosne, A.G.; Bergstrand, M.; Karlsson, M.O. An automated sampling importance resampling procedure for estimating parameter uncertainty. J. Pharm. Pharm. 2017, 44, 509–520. [Google Scholar] [CrossRef] [Green Version]
- Dosne, A.G.; Bergstrand, M.; Harling, K.; Karlsson, M.O. Improving the estimation of parameter uncertainty distributions in nonlinear mixed effects models using sampling importance resampling. J. Pharm. Pharm. 2016, 43, 583–596. [Google Scholar] [CrossRef] [Green Version]
- Bergstrand, M.; Hooker, A.C.; Wallin, J.E.; Karlsson, M.O. Prediction-corrected visual predictive checks for diagnosing nonlinear mixed-effects models. AAPS J. 2011, 13, 143–151. [Google Scholar] [CrossRef] [Green Version]
- Henquell, L.; Odoroff, C.L.; Honig, C.R. Intercapillary distance and capillary reserve in hypertrophied rat hearts beating in situ. Circ. Res. 1977, 41, 400–408. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Forster, J.C.; Harriss-Phillips, W.M.; Douglass, M.J.; Bezak, E. A review of the development of tumor vasculature and its effects on the tumor microenvironment. Hypoxia 2017, 5, 21–32. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tang, L.; Gabrielson, N.P.; Uckun, F.M.; Fan, T.M.; Cheng, J. Size-dependent tumor penetration and in vivo efficacy of monodisperse drug-silica nanoconjugates. Mol. Pharm. 2013, 10, 883–892. [Google Scholar] [CrossRef] [Green Version]
- Chauhan, V.P.; Stylianopoulos, T.; Martin, J.D.; Popovic, Z.; Chen, O.; Kamoun, W.S.; Bawendi, M.G.; Fukumura, D.; Jain, R.K. Normalization of tumour blood vessels improves the delivery of nanomedicines in a size-dependent manner. Nat. Nanotechnol. 2012, 7, 383–388. [Google Scholar] [CrossRef] [Green Version]
- Xie, F.; De Clercq, K.; Vervaet, C.; Van Bocxlaer, J.; Colin, P.; Vermeulen, A. Model-based analysis of treatment effects of paclitaxel microspheres in a microscopic peritoneal carcinomatosis model in mice. Pharm. Res. 2019, 36, 127. [Google Scholar] [CrossRef]
- Mahmood, I. Naive pooled-data approach for pharmacokinetic studies in pediatrics with a very small sample size. Am. J. 2014, 21, 269–274. [Google Scholar] [CrossRef]
- Dash, S.; Murthy, P.N.; Nath, L.; Chowdhury, P. Kinetic modeling on drug release from controlled drug delivery systems. Acta Pol. Pharm. 2010, 67, 217–223. [Google Scholar]
- Paul, D.R. Elaborations on the Higuchi model for drug delivery. Int. J. Pharm. 2011, 418, 13–17. [Google Scholar] [CrossRef]
- Simeoni, M.; Magni, P.; Cammia, C.; De Nicolao, G.; Croci, V.; Pesenti, E.; Germani, M.; Poggesi, I.; Rocchetti, M. Predictive Pharmacokinetic–Pharmacodynamic modeling of tumor growth kinetics in xenograft models after administration of anticancer agents. Cancer Res. 2004, 64, 1094–1101. [Google Scholar] [CrossRef] [Green Version]
- Yang, J.; Mager, D.E.; Straubinger, R.M. Comparison of two pharmacodynamic transduction models for the analysis of tumor therapeutic responses in model systems. AAPS J. 2010, 12, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Zhang, W.; Fan, W.; Rachagani, S.; Zhou, Z.; Lele, S.M.; Batra, S.K.; Garrison, J.C. Comparative Study of Subcutaneous and Orthotopic Mouse Models of Prostate Cancer: Vascular Perfusion, Vasculature Density, Hypoxic Burden and BB2r-Targeting Efficacy. Sci. Rep. 2019, 9, 11117. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dai, L.; Lu, C.; Yu, X.I.; Dai, L.J.; Zhou, J.X. Construction of orthotopic xenograft mouse models for human pancreatic cancer. Exp. Med. 2015, 10, 1033–1038. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, Y.; Toneri, M.; Ma, H.; Yang, Z.; Bouvet, M.; Goto, Y.; Seki, N.; Hoffman, R.M. Real-Time GFP Intravital Imaging of the Differences in Cellular and Angiogenic Behavior of Subcutaneous and Orthotopic Nude-Mouse Models of Human PC-3 Prostate Cancer. J. Cell Biochem. 2016, 117, 2546–2551. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Zhu, X.; Han, M.; Hao, F.; Lu, W.; Zhou, T. Mechanistic Pharmacokinetic/Pharmacodynamic Model of Sunitinib and Dopamine in MCF-7/Adr Xenografts: Linking Cellular Heterogeneity to Tumour Burden. AAPS J. 2020, 22, 45. [Google Scholar] [CrossRef]
- Li, J.Y.; Ren, Y.P.; Yuan, Y.; Ji, S.M.; Zhou, S.P.; Wang, L.J.; Mou, Z.Z.; Li, L.; Lu, W.; Zhou, T.Y. Preclinical PK/PD model for combined administration of erlotinib and sunitinib in the treatment of A549 human NSCLC xenograft mice. Acta Pharm. Sin. 2016, 37, 930–940. [Google Scholar] [CrossRef] [Green Version]
- Badr, C.E. Bioluminescence imaging: Basics and practical limitations. Methods Mol. Biol. 2014, 1098, 1–18. [Google Scholar] [CrossRef]
- Bulitta, J.B.; Zhao, P.; Arnold, R.D.; Kessler, D.R.; Daifuku, R.; Pratt, J.; Luciano, G.; Hanauske, A.R.; Gelderblom, H.; Awada, A.; et al. Mechanistic population pharmacokinetics of total and unbound paclitaxel for a new nanodroplet formulation versus Taxol in cancer patients. Cancer Chemother. Pharm. 2009, 63, 1049–1063. [Google Scholar] [CrossRef]
- Fernandes Neto, J.M.; Nadal, E.; Bosdriesz, E.; Ooft, S.N.; Farre, L.; McLean, C.; Klarenbeek, S.; Jurgens, A.; Hagen, H.; Wang, L.; et al. Multiple low dose therapy as an effective strategy to treat EGFR inhibitor-resistant NSCLC tumours. Nat. Commun. 2020, 11, 3157. [Google Scholar] [CrossRef]
- Gray, R.; Bradley, R.; Braybrooke, J.; Liu, Z.; Peto, R.; Davies, L.; Dodwell, D.; McGale, P.; Pan, H.; Taylor, C.; et al. Increasing the dose intensity of chemotherapy by more frequent administration or sequential scheduling: A patient-level meta-analysis of 37 298 women with early breast cancer in 26 randomised trials. Lancet 2019, 393, 1440–1452. [Google Scholar] [CrossRef] [Green Version]
- Krueger, T.E.G.; Thorek, D.L.J.; Denmeade, S.R.; Isaacs, J.T.; Brennen, W.N. Concise Review: Mesenchymal Stem Cell-Based Drug Delivery: The Good, the Bad, the Ugly, and the Promise. Stem Cells Transl. Med. 2018, 7, 651–663. [Google Scholar] [CrossRef] [Green Version]
- Layek, B.; Shetty, M.; Nethi, S.K.; Sehgal, D.; Starr, T.K.; Prabha, S. Mesenchymal Stem Cells As Guideposts for Nanoparticle-Mediated Targeted Drug Delivery in Ovarian Cancer. Cancers 2020, 12, 965. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Murry, D.J.; Blaney, S.M. Clinical pharmacology of encapsulated sustained-release cytarabine. Ann. Pharm. 2000, 34, 1173–1178. [Google Scholar] [CrossRef] [PubMed]
- Harper, E.; Dang, W.; Lapidus, R.G.; Garver, R.I., Jr. Enhanced efficacy of a novel controlled release paclitaxel formulation (PACLIMER delivery system) for local-regional therapy of lung cancer tumor nodules in mice. Clin. Cancer Res. 1999, 5, 4242–4248. [Google Scholar] [PubMed]








Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, S.; Nethi, S.K.; Al-Kofahi, M.; Prabha, S. Pharmacokinetic—Pharmacodynamic Modeling of Tumor Targeted Drug Delivery Using Nano-Engineered Mesenchymal Stem Cells. Pharmaceutics 2021, 13, 92. https://doi.org/10.3390/pharmaceutics13010092
Cheng S, Nethi SK, Al-Kofahi M, Prabha S. Pharmacokinetic—Pharmacodynamic Modeling of Tumor Targeted Drug Delivery Using Nano-Engineered Mesenchymal Stem Cells. Pharmaceutics. 2021; 13(1):92. https://doi.org/10.3390/pharmaceutics13010092
Chicago/Turabian StyleCheng, Shen, Susheel Kumar Nethi, Mahmoud Al-Kofahi, and Swayam Prabha. 2021. "Pharmacokinetic—Pharmacodynamic Modeling of Tumor Targeted Drug Delivery Using Nano-Engineered Mesenchymal Stem Cells" Pharmaceutics 13, no. 1: 92. https://doi.org/10.3390/pharmaceutics13010092
APA StyleCheng, S., Nethi, S. K., Al-Kofahi, M., & Prabha, S. (2021). Pharmacokinetic—Pharmacodynamic Modeling of Tumor Targeted Drug Delivery Using Nano-Engineered Mesenchymal Stem Cells. Pharmaceutics, 13(1), 92. https://doi.org/10.3390/pharmaceutics13010092