Fraud Detection Using Neural Networks: A Case Study of Income Tax

Abstract

Detecting tax fraud is a top objective for practically all tax agencies in order to maximize revenues and maintain a high level of compliance. Data mining, machine learning, and other approaches such as traditional random auditing have been used in many studies to deal with tax fraud. The goal of this study is to use Artificial Neural Networks to identify factors of tax fraud in income tax data. The results show that Artificial Neural Networks perform well in identifying tax fraud with an accuracy of 92%, a precision of 85%, a recall score of 99%, and an AUC-ROC of 95%. All businesses, either cross-border or domestic, the period of the business, small businesses, and corporate businesses, are among the factors identified by the model to be more relevant to income tax fraud detection. This study is consistent with the previous closely related work in terms of features related to tax fraud where it covered all tax types together using different machine learning models. To the best of our knowledge, this study is the first to use Artificial Neural Networks to detect income tax fraud in Rwanda by comparing different parameters such as layers, batch size, and epochs and choosing the optimal ones that give better accuracy than others. For this study, a simple model with no hidden layers, softsign activation function performs better. The evidence from this study will help auditors in understanding the factors that contribute to income tax fraud which will reduce the audit time and cost, as well as recover money foregone in income tax fraud.

1. Introduction

Income tax, along with other taxes, has long been a significant source of government revenues, which are then used to support public services, pay government debts, and contribute to a country’s development goals. This is a tax imposed by the government on many types of earnings made by individuals and businesses, and it varies depending on the amount gained through wages, salaries, and the business’s individual circumstances, to mention a few [1]. Despite the fact that many people understand the necessity of paying income taxes, taxpayers have been progressively developing new methods of income tax evasion that are naturally difficult to detect, necessitating the employment of more modern and strong methods of tax fraud detection, as [2] stated.

Although income tax fraud is a hot topic in Rwanda, there have not been enough studies conducted to determine the extent of the problem and the amount of money lost as a result of it. According to [3], over Rwf 20 billion have been lost in the five years since 2016 due to tax fraud. The majority of these cases were discovered using traditional methods of random auditing and sometimes whistle-blowing and tip-off methods, which is also the case on a global scale, as revealed by the [4] global survey conducted by KPMG, which investigated 750 fraudsters between March 2013 and August 2015 and discovered that only 3% of these fraud cases have been identified using data analytics and machine learning, while 44% were discovered using intuition and aforementioned traditional methods.

According to [5], the most commonly used fraud detection methods are rule-based systems, which are no longer effective enough given that auditors go through the income tax records of millions of individuals and businesses and rely on knowledge, experience, and intuition to determine whether or not there was tax fraud. As stated by [6], this method has two drawbacks: it relies largely on past experience, which means it mostly misses new fraud tactics; and it is knowledge-based, which makes it expensive to maintain and update.

While fraudsters are continually developing new tactics to avoid paying taxes, it is no longer possible to track them just using human knowledge and intuition or hope that auditors will notice. Fortunately, machine learning has transformed the way we do things in a variety of fields, including fraud detection. Although they were not focused on income taxes, several studies [6,7,8] employed supervised and unsupervised machine learning methods, and while much of the research used unsupervised machine learning due to the scarcity of labeled data, supervised machine learning produced better and more accurate outcomes in detecting tax fraud.

Numerous authors have suggested that Artificial Neural Networks (ANN) be employed for fraud detection in general. The study conducted by [9] compared Artificial Neural Networks (ANN), support vector machines (SVM), and K-Nearest Neighbours, and the results showed that ANN outperform other models. It was also recommended that ANN should be more employed in fraud detection because it is best suited for detecting credit card fraud. In a study conducted by [10] to detect fraud for Mellon Bank, ANN was proven to enhance accuracy and timeliness. ANN was also compared to decision trees and Naive Bayes on financial data in order to detect fraud, and as a result, multi-layer perceptron performed well in terms of accuracy (97.47%), and it has been recommended to be used for fraud detection [11].

With the availability of labeled data mainly from tax collection institutions, the efforts to apply supervised machine learning algorithms for fraud detection are considered significant. Nevertheless, not much has been achieved, especially on income tax fraud. Subsequently, the purpose of this research is to explore how different neural network algorithms might be used on income tax-related data from the Rwanda Revenue Authority (RRA), with an emphasis on identifying factors and therefore detecting income tax fraud in Rwanda. This study compared different parameters such as activation, batch size, epochs, layers and others and then choose the optimal number of each parameter that helped to obtain good accuracy. To the best of our knowledge, it is the first study to use a neural network by using the optimal parameter for the real income tax data for Rwanda.

The rest of the paper is organized as follows. Section 2 focuses on related work. Section 3 describes the Artificial Neural Networks model that was used in this research. The study’s results and discussion are presented in Section 4. Section 5 concludes the work with a brief conclusion and future research areas.

2. Related Work

It was not long ago that artificial intelligence and machine learning became the most promising field for solving complex issues by leveraging the computer’s ability to learn from available data. Among the first studies to have employed fraud focused data analytics and machine learning include [12,13].

As noted by [14], while most studies addressing tax fraud detection employ supervised learning, the lack of historically labeled data limits such studies in most situations since manual auditing and labeling data is expensive and time-consuming. As a result, they proposed using unsupervised learning. This research was divided into three phases: clustering similarly valued tax declarations; adjusting probability distribution to each cluster tax base, and detecting suspicious activities by checking the quantiles of cluster adjusted distribution. Despite the fact that their model produced promising results, there was the limitation of the limited amount of data, and a low number of variables needed to deeply describe cases. The most worrying issue was that the model’s accuracy would not be evaluated because the data was not labeled, which raises questions about its trustworthiness.

In ref. [15] study, the multilayer perceptron neural network model was used to identify fraud in personal income tax forms. According to the authors, this model outperforms other predictive models in predictive ability and is the least expensive because it does not take into account some statistical criteria such as normality, incorrect processing of data, and others. Their findings demonstrated that the multilayer perceptron is effective for efficiently classifying fraudulent and non-fraudulent taxpayers, as well as determining each taxpayer’s likelihood of cheating tax. According to their suggestion, the technique could be used to detect fraud behaviors in other types of taxes.

The Hybrid Unsupervised Outlier Detection (HUNOD) model was developed by [16] to detect suspicious tax behaviors by incorporating user knowledge into a combination of clustering and representational learning to identify outliers from personal income tax data. Identified outliers were interpreted using an “explainable-by-design surrogate model” which was trained on internally validated outliers. This model was effective, as it was able to identify between 90% and 98% of outliers.

As ref. [15] stated, Artificial Neural Networks (ANN) make it easy to handle bigger datasets and, despite their algorithms being complex, it gives easily interpretable results, which is why they are popular in the financial sector, marketing, forecasting, and more often in risk assessment and fraud detection. The current study applies Artificial Neural Networks to the real data set to detect factors related to income tax fraud. The approach will help to reduce the time, effort, and cost taken by auditors in the manual identification of cases to audit. It will also help to combat income tax fraud, as well as recover money lost to tax fraud. To the best of our knowledge, this is the first study to employ Artificial Neural Networks to detect income tax fraud in Rwanda using optimal parameters, and it considers both domestic and cross-border businesses. Different parameters such as layers, epochs, and others were compared and assessed, and the optimal ones were employed in our model to produce good results.

For the study on financial prediction by [17] where they have compared Deep Convolutional Neural Networks(DCNN) and Multilayer Perceptron (MLP). They used MLP with 8 layers and DCNN with 13 layers to develop a credit scoring model. Their models were compared on German and Australian credit scoring data. For the two evaluation indices utilized to compare the performance of these models, such as overall accuracy and missed alarm rate, the experimental findings demonstrated that DCNN was significantly better than MLP. The DCNN accuracies for German and Australian data were 90.85% and 99.74%, respectively. The accuracies for MLP were 81.20% and 90.17%, respectively.

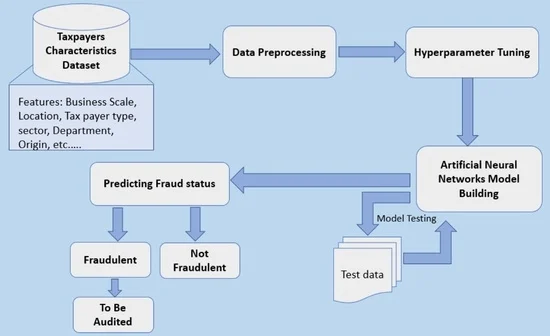
3. Methodology

Recently, researchers have taken a renewed interest in Artificial Neural Networks (ANN) owing to their functional structure and being at the core of deep learning. Just as birds inspired the construction of the airplane, the human brain motivated the development of ANN with the objective of imitating the functioning structure of the human brain in order to enable a computer to learn in the same way that people do. Thus, ANN was created as a replication of the generalized mathematical model of the human central nervous systems [18,19].

ANNs are defined as sets of algorithms that use techniques similar to how the human brain works in an attempt to detect hidden relationships in data. The networks are mainly systematical neurons that share information and are versatile in the sense that during the training process, networks take data and train themselves to recognize the patterns in this data [18,20].

The design of a multi-layer perceptron must have at least one hidden layer added to the input and the output layers. The most common algorithm for fitting multi-layer perceptron models is the back propagation learning algorithm in which errors are transferred backward through the network so that the process can begin again with adjusted weights for better accuracy [20].

3.1. Structure of Artificial Neural Networks

The smallest element of any ANN is a neuron, also known as a node. See Figure 1, a neuron structure and sample ANN Multi-layer perceptron structure. These are connected by synapses, which also define how strong the connection is using the weight. The synapse is mathematically represented as a weight vector, and this weight decides how the preceding layer’s output is routed via the activation function for each node. Each neuron or perceptron is characterized by its input, an activation function, and the output provided [19].

A neuron’s inputs $x_0,x_1,\cdots ,x_n$ with their corresponding weights $w_0,w_1,\cdots ,w_n$ are processed by an activation function, and the result is the neuron’s output, which corresponds to:

$$Output=f(w_1{x}_1+w_2{x}_2+\cdots +w_n{x}_n+bias)=f\left(\sum _{i=1}^n{x}_i{w}_i+bias\right),$$

(1)

where $x_i$ and $w_i$ are the input vector and weight vector, respectively, f is the activation function applied on the sum of products of each input and its associated weight and the bias.

An activation function of a neuron in an ANN defines the neuron’s output given a set of inputs. They convert input signals into output, which is then fed as input to the next layer in a network. This function is designed to introduce non-linearity in a network by either activating or deactivating a perceptron [23]. In its optimization process, ANN employs optimizers such as gradient descent to minimize prediction errors; the prediction error is computed using a loss function, which quantifies how good or bad the model performance is. Optimizers modify a perceptron’s weight and bias, as well as the network’s learning rate, to reduce the loss function as much as possible, thereby improving the model’s performance [24].

3.2. Model Architecture

In Artificial Neural Networks, just as it is critical to have high-quality data, it is also critical to select appropriate parameters for the problem at hand. The activation function is one of the most important parameters because it plays a significant role in aggregating signals into the output signal that is propagated to the other neurons in the network, as well as processing information and passing it throughout the network.

According to [25], without an activation function, any ANN is just a simple linear function. Despite the fact that linear equations are simple and straightforward to solve, they are limited in their complexity, and they lack the ability to learn and discover complicated data mappings. Most of the time, a neural network without an activation function acts as a linear regression model with low performance and capacity. It is preferable for a neural network to perform tasks other than learning and computing a linear function, such as modelling complex tasks. Sigmoid, ReLu, softmax, softsign, linear, hard-sigmoid, softplus, and others were tested using the grid search to determine which activation function is best suited for income tax fraud detection.

Sigmoid is the most commonly utilized activation function because it is a non-linear function that may convert and squash numbers in the range of 0 to 1. It is critical to have a sigmoid activation function on the output layer in cases of binary classification [23].

A rectified linear unit (ReLU), also known as a piecewise linear function, works in such a way that it will output the input directly if it is positive, or zero otherwise. This function is widely used in neural networks and is widely assumed to be more efficient than others since neurons are not activated all at once, but instead, a subset of neurons are activated at a time. It is recommended that this function be tried first because numerous studies have shown that it performs well in a variety of tasks [23,26].

Softmax is a function that converts numbers into probabilities. A Softmax’s output is a vector containing the probabilities of each possible outcome. For all possible outcomes or classes, the probabilities in a vector sum to one. It is widely used as a neural network’s final activation function to standardize network output to a probability distribution over expected output classes. We can consider sigmoid function values as probabilities of data points from a certain class because we know they range from 0 to 1. The softmax function, unlike sigmoid functions, can be used for multiclass classification tasks [23,26]. The softsign function has more robust synchronization than softmax due to its smoother asymptotic line and comparatively slow and soft saturation. The softsign function activation value is distributed uniformly in a large number of nonlinear yet good area gradient flows. Because the softsign activation function is nonlinear, it detects errors more effectively [27].

Among other commonly used activation functions is a hard-sigmoid. This activation function has a lower computation cost than a sigmoid activation function. It has shown promising results on binary classification tasks when implemented. A hard sigmoid is a sigmoid activation function generalization. It is almost linear, so it is much faster and less expensive to compute than a standard sigmoid activation function [28].

Finally, the softplus activation function was used; this function has several advantages, including being smooth in the definition domain. This property makes the softplus function more stable regardless of whether it is estimated in the positive or negative direction. Another benefit is that the softplus unit has a non-zero gradient even when the unit’s input is negative. Gradients can be propagated by the softplus function across all inputs [29].

According to [30], the batch size is a parameter that controls how many complete passes through the training dataset are made. It sets the minimum number of samples that must be processed before the internal model parameters can be updated. The size of a batch might range from one to a few hundred. The smaller the batch size, the faster the learning process converges at the expense of training process noise, whereas the larger the batch size, the slower the learning process converges with accurate error gradient estimations. Before deciding on the optimal batch size, it is recommended to experiment with various batch sizes.

The number of epochs is a parameter that determines how many times the learning algorithm will iterate through the full training dataset. It controls how many times the training dataset is examined completely. This number can be anywhere between one and infinity, however, the greater the dataset, the higher the epochs number should be, allowing the learning method to run until the model’s error is adequately minimized. When specifying this option, there are no hard and fast rules. It is only necessary to experiment with different values and see what works best for the problem [30].

Using Grid Search for hyper-parameter tuning, combinations of many parameters mentioned above were tried to see which combination is the most accurate in classifying fraudulent and non fraudulent taxpayers. In total, 576 different combinations were tested and even if we cannot show them all in this paper,

Table 1. Hyper-parameter tuning.

Activation	Batch	Epochs	Layers and Neurons	Train Acc	Val Acc	Test Acc
sigmoid	40	30	[50]	0.8672	0.8643	0.8703
sigmoid	40	50	[50, 40, 30, 20, 10]	0.7918	0.7769	0.7891
relu	40	30	[50]	0.8948	0.8871	0.8929
relu	128	50	[50, 20]	0.8989	0.8889	0.8954
softsign	80	100	[50, 40, 30, 20, 10]	0.7918	0.7769	0.7891
softsign	40	100	[20]	0.9069	0.8889	0.8954
softsign	40	100	[50]	0.8979	0.8889	0.8954
linear	80	100	[60, 45, 30, 15]	0.9002	0.8862	0.8920
linear	128	100	[50, 40, 30, 20, 10]	0.8982	0.8889	0.8954
hard_sigmoid	100	100	[50]	0.8756	0.8670	0.8780
hard_sigmoid	40	100	[60, 45, 30, 15]	0.7918	0.7769	0.7891
softplus	80	100	[50]	0.8968	0.8889	0.8954
softmax	128	50	[50,20]	0.7918	0.7769	0.7891
softmax	40	30	[50, 40, 30, 20, 10]	0.7918	0.7769	0.7891

illustrates some of those parameter combinations, as well as how accurate each one was in regards to the training accuracy, validation accuracy and test accuracy. It also indicates how many layers are there, with each layer having a different number of neurons.

In some cases, the train and test data may not have been chosen in a consistent manner, and some unexpected extreme cases may occur in the test data, lowering the model’s performance. As a result, cross-validation is critical to reducing the risk of over-fitting and improving model robustness. In this study, the k-fold cross-validation method with 5 folds was used. The model train is run five times, each time with a different subset of data excluded for validation, and the final accuracy is the mean of the five recorded accuracies [31].

Based on the training, validation and testing accuracy, we can see from Table 1 that the best model with the best train, validation and test accuracy is the simple one with no hidden layers, with 40 batch size, 100 epochs, and only a 20-neuron input layer, denoted as [20]. Different numbers of layers such as simple ones without hidden layers were tested in order to find the best ones that gives the better accuracy for train, validation, and test. From the results of different combinations of layers with different numbers of neurons, it is revealed that the model becomes less accurate as the number of layers increases, as evidenced by the accuracy obtained when we use a 50-neuron input layer coupled with four hidden layers with 40, 30, 20, and 10 neurons, respectively, denoted as [50, 40, 30, 20, 10]. The softsign activation was the optimal one among others. Softsign activation is a robust activation where its values are distributed uniformly in a large number of non-linear. Because of its smoother asymptotic line and slow and soft saturation, softsign offers a more durable synchronization.

After experimenting with various parameters and layer counts, it was shown that the best model to train would consist of only an input layer and an output layer. According to Table 1, the optimal parameters have a training accuracy of 90.69%, a validation accuracy of 88.89%, and a test accuracy of 89.54% which is a bit higher compared to others.

3.3. Model Evaluation

As the loss function and optimizer, binary cross-entropy was used. The binary cross-entropy, also called log-loss, is a loss function that is well suited for binary classification tasks, as it compares predicted probabilities to actual classes by measuring the distance between the prediction and actual output when training and the computed log-loss shows how close or far the prediction is to the actual values [32].

$$\mathrm{Loss}=-\frac{1}{N}\sum _{i=1}^N{y}_i\times log\left(p\left(y_i\right)\right)+\left(1-y_i\right)\times log\left(1-p\left(y_i\right)\right)=-\sum _{i=1}^{\mathrm{N}}{y}_i\times log\left(p\left(y_i\right)\right),$$

(2)

where $y_i$ is the actual class and $log\left(p\left(y_i\right)\right)$ is the probability of that class and $p\left(y_i\right)$ is the probability of 1 while $(1-p\left(y_i\right))$ is the probability of 0.

When training, an optimizer is used to minimize the loss, and Adamax was found to be the best optimal as per the grid search hyperparameter tuning performed and was eventually used in this study. Accordingly to Kingma [33], Adamax, which is based on infinity norm, is a variant of Adam optimizer which is an efficient stochastic method that computes individual adaptive learning rates for different parameters. This optimizer is sometimes superior to Adam especially when representing many discrete features which makes it well suited for bigger datasets with discrete variables like in this research.

3.4. Confusion Matrix

A confusion matrix is a popular measurement tool for classification models; it displays a matrix representation of predicted values in comparison to actual values. It is mainly beneficial to examine a model’s precision and recall capacity, as well as its accuracy and Area Under the Curve [24]. To understand terms used in the confusion matrix such as the True Positive (TP), False Positive (FP), True Negative (TN) and False Negative (FN), we use this research’s case:

• True Positives (TP) are cases in which the taxpayer is predicted to be a fraudster and is, in fact, a fraudster.
• False Positives (FP) are cases in which the taxpayer is predicted to be a fraudster and is actually not a fraudster. This is also known as Type I error.
• True Negatives (TN) are cases in which the taxpayer is predicted not to be a fraudster and is not a fraudster.
• False Negatives (FN) are cases in which the taxpayer is predicted not to be a fraudster and is actually a fraudster. This case is most known as the Type II error, and it is a very risky error especially in tax fraud detection.
• Accuracy is the ratio of observations that are correctly predicted to the total observations and the formula is shown in below equation [24,26].

  $$\mathrm{Accuracy}=\frac{TP+TN}{TP+FP+TN+FN}$$

  (3)
• Precision highlight how accurate is the model on predicting the positive classes, i.e., how many of the predicted positive are actually positive [26,31].

  $$\mathrm{Precision}=\frac{TP}{TP+FP}$$

  (4)
• Recall highlight how many from the actual positives are predicted as positives. although it sounds simple, this is a very crucial metric for the tax fraud issue because there is much more risk and cost in predicting a taxpayer non fraudulent while they are fraudulent [26,31].

  $$\mathrm{Recall}=\frac{TP}{TP+FN}$$

  (5)
• F1 Score as a function of recall and precision, the F1 Score is usefully to examine how much of a balance is between the precision and recall [26,31].

  $$\mathrm{F}1\mathrm{Score}=\frac{2\times Recall\times Precision}{Recall+Precision}$$

  (6)

3.5. Feature Importance Evaluation

According to Heaton [34], feature importance evaluation refers to methods of assigning scores to independent features of a predictive model, with the score indicating the relative contribution of each feature to the model’s prediction accuracy. Artificial Neural Networks have been described as black box types of models in a way that despite approximating any function, the neural network’s approximation will provide no insight into the form of that function, making it difficult to interpret and evaluate input feature relevance to the model [34].

Fortunately, many studies have been conducted to address this issue, and some have yielded useful results. Ref. [35] proposed the “Variance-based Feature Importance in Neural Networks” which works well on either classification or regression tasks. The Welford online algorithm was used to compute the running weight of each input during training by assuming that the important features will have more weights on its input neurons and that this weight will vary throughout the training process. Following training, the variance of the weights for each input is added together to calculate the cumulative weight, which determines how important the features are. The Welford’s algorithm is preferred because of its high performance in calculating statistics such as variance and averages for one-pass online learning tasks such as in neural networks, where each layer’s output is the input of the next layer with its weight and it is only used once [36].

4. Results and Discussion

In this section, we look at the data used, present and discuss the results obtained from the computations, and explain what these results mean in regard to income tax fraud detection.

4.1. Data Description and Pre-Processing

The used data in this research was obtained from the Rwanda Revenue Authority, the national body in charge of tax collection in Rwanda. The dataset consisted of 7840 audited taxpayers from across the country, with 1655 (21.1%) found guilty of fraud and 6185 (78.9%) cleared of any tax fraud. Each taxpayer was identified by features such as Province, Business scale, Sector, Business origin Department, Operation time and others. For feature exploration,

Table A1. Features explanation.

Features and values	Frequency	Non Fraudulent	Fraudulent
Province
KIGALI CITY	5715	4550	1165
EAST	580	515	65
WEST	580	400	180
SOUTH	525	345	180
NORTH	440	375	65
Scale
SMALL	6300	5015	1285
MEDIUM	680	490	190
MICRO	475	445	30
LARGE	385	235	150
Tax Payer Type Desc
NON INDIVIDUAL	4295	3250	1045
INDIVIDUAL	3545	2935	610
Registration Status
Yes	7835	6185	1650
NO	5	0	5
Sector
Services	6585	5145	1440
Industry	1155	950	205
Agriculture	95	85	10
OTHERS	5	5	0
Department
Customs	5335	4550	1165
Domestic	580	515	65
Filing Status
ONTIME	7360	5800	1560
LATE	480	385	95
Time of Business (years)
0–5	7360	5800	1560
6–10	480	385	95
11–15	480	385	95
16–Above	480	385	95
Business origin
National	7835	6185	1650
International	5	0	5

provides a comprehensive view of the dataset and the important features in it. There were no missing or duplicate values in our data. There was no outliers since our data set was composed of categorical variables except one variable that indicates the difference in time from when a business was registered to the time of audit that was composed of integers.

As some of the features, such as scale, department, and others, are categorical, it was necessary to create a dummy variable that would allow those features to be used in a model. Dummy variables are variables derived from qualitative or logical propositions that are not numerical in nature. They can only hold numerical values of 0 or 1, representing qualitative values by switching various parameters on and off [37]. Example: The Business Scale (Scale) feature holds values such as Large, Medium, Small, and Micro, which result in four dummy variables, namely Scale_large, Scale_medium, Scale_small, Scale_micro, of which only one is on (1) and the other three are off (0) based on business Scale. Dummy variables representing each category were created for the categorical variables, increasing the number of features from 11 to 54.

There was an imbalance in our data because, out of 7840 data points of taxpayers, 6185, or 78.8%, were labeled as non-fraudulent, while only 1655, or 21.2%, were labeled as fraudulent. To address such issues, a combination of both under-sampling and over-sampling methods were used, namely the Random Under sampling(RUS) and the synthetic minority over-sampling technique (SMOTE). This is because the dataset is quite small and dropping a lot of majority observations would result in a significant loss of information needed in a model while only oversampling would increase the likelihood of overfitting.

RUS is straightforward under-sampling method that randomly removes data points from the majority class in order to balance the dataset [38]. While using SMOTE, each minority class sample is over-sampled by introducing synthetic examples similar to k minority class nearest neighbors. Neighbors from the k nearest neighbors are chosen at random depending on the amount of oversampling required [39].

After resampling, the remaining dataset was of 4000 data points which was divided into training and testing ratios of 80% and 20%, respectively.

4.2. Results

After data preparation, Artificial Neural Networks with optimal parameters were applied. The training process was evaluated using training and evaluation loss, as well as the accuracy. Before dealing with imbalance, the model gives an accuracy of 90% but a very low precision of 68% which calls for questions about the model’s ability to classify. The Area Under Receiver Characteristic Curve (AUC-ROC) for the original data was 94%. After dealing with the imbalance, accuracy was 92% and precision goes to 85%. The AUC-ROC after dealing with the data imbalance was 95%. The oversampling method made the model much more accurate and precise.

From the learning curves above in Figure 2, it can be seen that the training loss kept on dropping throughout the process, which is the same for the validation loss. On the contrary, the training and testing accuracy look to have reached the maximum level mid way through training. From the learning curves, the results are promising, and next is testing the model to verify if it does not over-fit.

4.3. Test Result

For the performance evaluation of any classification model, the confusion matrix is the first and easiest way to use so as to compare the actual class with the predicted one, as well as compute the model’s precision and recall. As it is seen on the below test confusion matrix Figure 3, more than 700 taxpayers were correctly predicted while 2 were predicted as non fraudulent when they were fraudulent, and 49 were predicted as fraudulent when they were not.

From the test confusion matrix, the results look promising, despite some taxpayers being predicted as fraudulent even if they are not, the model is trustworthy as it captures almost all the fraudulent taxpayers, which is the main goal. Many other evaluation metrics have been used and the collective outcomes suggest that ANN would be a considerable solution to income tax fraud detection. Among those other metrics are F1 Score and AUC-ROC as it is shown in

Table 2. Model Evaluation.

Metric	Original Data	Re-Sampled Data
Accuracy	0.90	0.92
Precision	0.68	0.85
Recall	0.99	0.99
F1 score	0.79	0.92
AUC-ROC	0.94	0.95

and Figure 4 below.

4.4. Important Features

The Variance-based feature Importance of Artificial Neural Networks (VIANN) was used to evaluate how important the features to the model’s performance are. VIANN assumes that important features will have a higher weight on its corresponding input neuron, and this will change as the training progresses, it is based on Welford’s online algorithm, which is well known for computing the online variance. Following training, the variances of the weights are combined with the final weights to determine how important each input feature is [35].

Through feature importance evaluation using VIANN, a number of features proved to be very important to the income model’s accuracy, where the top 15 features based on their importance are as follows: The Customs Department (0.5447) was the most important, followed by the Domestic Department (0.3496), Time of Business (0.2799), Scale_Small (0.2636) and others. The importance values tend to vary as the model is re-run, but a small number of features shown in

Table 3. Feature importance.

Features	Importance
Department_Customs	0.5447
Department_Domestic	0.3496
Time of Business	0.2799
Scale_SMALL	0.2636
Tax Payer Type Desc_NON INDIVIDUAL	0.1553
Tax Payer Type Desc_INDIVIDUAL	0.1341
District Name_KICUKIRO	0.0838
Scale_LARGE	0.0830
District Name_NYARUGENGE	0.0796
Scale_MICRO	0.0777
District Name_GASABO	0.0761
Sector_Services	0.0697
Scale_MEDIUM	0.0625
Sector_Industry	0.0624
Province_KIGALI CITY	0.0517

are found to be very important in every run, which highlight their influence on the model.

From the features in Table 3, the “Department” from which a taxpayer is registered is a big factor in whether the taxpayer is fraudulent or not. This variable shows that taxpayers who are doing cross-border businesses and those who are doing businesses domestically are all related to income tax fraud. The findings revealed that taxpayers who import and export goods and services are highly related to income tax fraud than those who are doing their businesses domestically. Moreover, the ’time of business’ which shows how long a business has been operating from the time of its registration to the time of the audit, was revealed to be an important factor in income tax fraud. Followed by “Scale” of business, where small scale businesses are more likely to be involved in income tax fraud than Large Scale businesses. The description of a taxpayer or business variable as either non-individual (company) or individual is also among the important variable for income tax fraud. While the location of a business is also another factor to consider, this shows that businesses in Kigali City districts are more likely to be found in income tax fraud than other districts. The features related to the income tax fraud identified by this study are consistent with the ones revealed by the previous submitted paper on predicting tax fraud using different supervised machine learning models [40]. That submitted paper covered the dataset with all tax types and the cross-border businesses, small businesses and time of the business were amongst features that are related to tax fraud.

Although more research is needed to delve deeply into the use of machine learning in tax fraud detection, this study has provided new insight into how tax fraud should be detected with minimal cost. Aside from demonstrating which characteristics are important when detecting fraud, the findings of this study are consistent with the previous study that compared different supervised machine learning models to a dataset with all tax types [40]. As [15] stated, neural networks not only distinguish between the fraudulent and non-fraudulent, but also compute the probability of one being fraudulent, which is useful in tax auditing and inspection so that tax auditing can be planned and focused on those with a high likelihood of being fraudulent or high risky departments like customs and small businesses.

5. Conclusions

The aim of this study was to employ Artificial Neural Networks to detect income tax fraud. It was found that there is no difference in income tax fraud between businesses that import and export goods (customs) and domestic businesses, except that customs businesses are more related to tax fraud than domestic businesses. The time of the business that shows the difference in time from when a business was registered to the time of audit was also revealed to be a feature that is related to tax fraud. Small businesses are also related to tax fraud, and this is because there are a large number of people with inadequate information and capital for their businesses and almost all with unstable businesses. Non-individual businesses (corporations) and individual enterprises were also proven to be tax fraud. The location variable shows that businesses located in Kigali City districts are more related to income tax fraud than other districts. This study’s findings are consistent with the previously submitted paper that covered all tax types by using different machine learning models where it revealed that businesses that import and export goods and services, small taxpayers and time of the business are among the variables that are more related to tax fraud.

It is worth mentioning that the model’s accuracy reduced as the number of layers increased, which is why the most accurate model had only an input and output layer.

The current study will reduce the auditing time and cost because the model is applied to a big data set and shows all features related to tax fraud, not one by one. This research will help to inform decision-makers in tax administrations and governments about potential factors of income tax fraud, allowing them to implement evidence-based and effective policy measures. This will also help in recovering money lost to income tax fraud as well as help the revenue authorities maintain the level of compliance of businesses registered for the income tax.

For future research, it will be interesting to use Deep Convolutional Neural Networks (DCNN) to see if they will perform better than Multilayer Perceptron (MLP).

It would also be useful to automate the model and create a real-time dashboard to help in the detection of tax fraud in general.