Embedding an Identity-Based Short Signature as a Digital Watermark

Abstract

Digital watermarking aims at protecting multimedia content by hiding into it some data that can be used for such purposes as, for example, intellectual property protection or integrity control. Sometimes, the owner of an image would prefer to not transmit, publish, or hand to a cloud service the original image, but rather an encrypted version of it. Encrypted images allow for less embedding room with respect to their unencrypted counterparts, as there is less spatial correlation to leverage upon. An architecture for embedding as payload the digital signature of an encrypted image, by means of a reversible watermarking technique, is presented in this work. A noteworthy point is the use of an identity-based cryptosystem to avoid certificate management and improve performance. In addition, the use of IBS-1, a recently proposed signature scheme, allows for a reduction in the size of the signature.

1. Introduction

Digital watermarking is a data hiding technique aimed at identifying and protecting digital multimedia content. In the embedding phase, steganographic data (the watermark) is hidden into the media content, in the detection phase the embedded watermark is extracted. A watermark is meant to not be easily removable or breakable. A classical taxonomy is indeed based on the resilience to alteration or removal by means of image modifications and distinguishes among fragile, semifragile, and robust watermarks. Robust watermarks are designed to resist to transformations. Semifragile watermarks are still retrievable after the image has undergone limited modifications. Fragile watermarks are destroyed by the slightest modification; their typical use is for integrity control.

A different taxonomy is related to the capability of recovering the original image exactly as it was before watermarking. In general, watermarking methods induce permanent modifications of the image they act upon. With reversible (also variably referred to as lossless or invertible) watermarks, the original image can, instead, be reconstructed unaltered. Reversible watermarks are especially used in application areas where no modification can be tolerated (e.g., forensics, digital archival of valuable content, or medical imaging). For example, if a watermarking technique induces modifications to medical images, a clinical trial may be necessary before such images can be used for diagnostic purposes.

Many watermarking methods rely on domain-specific knowledge. For instance, medical images are often partitioned into two different areas, which are dealt with differently. The ROI (Region of Interest) is defined as the region containing the portions of an image that have clinical significance, while the RONI (Region of Non-Interest) includes the background and possibly a contour. As the RONI contains less relevant data than the ROI, and can thus be subject to heavier modifications, robust watermarks are usually embedded there, leaving the ROI as unaltered as possible. Feature-based image watermarking schemes aim to survive geometric distortions, e.g., scaling, translation, rotation, and cropping. Such schemes isolate salient points of an image, such as corners and edges, which are supposed to be intrinsically bound to the image. Features are thus meant to survive distortions and re-compression. Geometric invariants could be computed from the original image or from a transform of it. A method for selecting the most adequate feature regions for robust watermarking, formulated as a multidimensional knapsack optimization problem (MDKP) and tackled by means of a Genetic Algorithm techniques is presented in [1].

There are situations in which the original image is not available to the embedding agent, who is only given an encrypted image. In such cases, embedding cannot capitalize on regularities and spatial correlation in the image or in some transform of it. Consequently, encrypted images can accommodate smaller payloads. In the context of watermarking encrypted images, assuming that two keys are used for the operations of encrypting and embedding, the property of separability guarantees that the encryption key and the embedding key need not be shared by the same detecting agent [2]. Possession of both keys grants full access, but an agent who only knows the embedding key is able to retrieve the embedded payload and has no access to the original image, whereas an agent who only knows the encryption key will not have access to the embedded payload but will still be able to see a slightly degraded image. The scheme by Zhang [2] works with a stream ciphering algorithm. In this work we consider the case of image encryption by means of Identity-Based encryption (IBE) [3]. In addition, the payload that is embedded into the encrypted image is its signature, again via an identity-based cryptosystem. The main innovation of our approach is the adoption of a digital signature scheme, named IBS-1, which offers short signatures by using elliptic curves. These proprieties practically allow a strong reduction of embedded payload size.

The outline of the paper is as follows. Related work is briefly discussed in Section 2. Identity-based short signatures are briefly recapitulated in Section 3. Our proposed strategy is described in Section 4. Finally, conclusions are drawn in Section 5.

2. Related Work

Reversible watermarking has consistently been a very active research area over recent years. Techniques for reversible watermarking fall into three main categories.

2.1. Lossless Compression

These techniques operate by substituting portions of the image (typically, a small number of the LSB planes) with the compressed concatenation of the original image portion and the payload [4].

2.2. Difference Expansion

Algorithms based of difference expansion (DE) use integer transforms having the property that, for some region of the input data, the reverse transform is tolerant to the manipulation of the LSB [5].

In [6], the technique was improved by using groups of n pixels instead of pairs. An example transform of a pair of values involves the use of the integer part of their average and their difference. A generalization for a generic integer transform was provided by [7]. To locate embedded pixels, a location map with one bit for each pixel pair is formed, compressed and embedded into the image as well. If pixel groups are used instead of single pixels, the size of the location map diminishes correspondingly.

2.3. Histogram Shifting

Histogram shifting (HS) [8] works on histograms of features; it creates space for embedding by selecting an histogram bin and shifting to the right (resp., to the left) by one position all features in the bins corresponding to values higher (resp., lower) than the one corresponding to the selected bin. In this way, the selected bin can be used, together with the emptied neighboring one, for embedding. As the embedding potential is related to the number of elements in the selected bin, features leading to peaked histograms were sought. Among these, residuals from prediction [9,10] provided good performance. Wang et al. [11] proposed the use for embedding of the smallest bins (at each tail of the histogram) that could provide the required capacity. In this way, distortion is kept under control. All reversible watermarking methods need, in fact, to strike a balance between high payload and low distortion. From the theoretical point of view, Zhang et al. [12] provided a recursive code construction for binary covers that can achieve the upper bound of the embedding rate under a given distortion constraint. As the title of their paper suggestively reports, they studied the relationship between reversible data hiding and lossless compression, a theme that has been extensively analyzed in literature [13,14]. Generally, the payload of DE-based methods is higher than the one achievable with HS-based ones. Conversely, image quality is, normally, better with HS-based methods than it is with DE-based ones.

In [15], the image is partitioned into two regions such that they correspond to separated areas in the interpolation-error histogram. Dragoi and Coltuc combined multiple predictors to leverage upon the changes in statistical properties from one portion of an image to another [16]. Puech et al. [17] used the Electronic Code Book (ECB) mode of the Advanced Encryption Standard (AES) algorithm and embedded 3 bits per block. Patches were used instead of single pixels, as an improvement of a reversible and separable watermarking scheme for encrypted images, in [18]. In [19], Zhang et al., proposed a lossless data hiding scheme for public-key-encrypted images, leveraging upon the homomorphic properties of some cryptosystems. They also proposed a distinction between the terms “lossless” and “reversible”, with the latter indicating that the cover medium can be perfectly recovered, while the former referred to the coincidence of the displayed data with the cover (even though the cover was altered to some extent).

3. Identity-Based Short Digital Signature

The concept of Identity-Based cryptography (IBC) was introduced by Adi Shamir [20] in 1984. It can be considered an alternative approach to public key certificates, motivated by the considerable computing overhead caused by certificate management operations (storing, checking, updating and revoking). In IBC, the public key of a user corresponds to the user’s identity, which can be easily represented as a free-text string (e.g., an e-mail address, an IP address). An Identity-Based cryptosystem relies on a trusted Private Key Generator (PKG), which generates the master secret key and a set of public parameters. Subsequently, starting from the identity of a user, the PKG extracts the corresponding private key, which is then sent to the user through a private and secure communication channel. Inherent in IBC is a known issue of key-escrow, since the PKG generates all private keys of users. A solution to this problem was proposed by Boneh and Franklin [3], employing multiple PKGs. Certificateless publick-key cryptography (CL-PKC), first proposed by Al-Riyami and Paterson in 2003 [21], is intended to address the key-escrow problem with a similar approach. In this case, PKG and user each give a partial contribution to the generation of the public/private key pair, so the PKG would not know the entire private key of the user. With CL-PKC, public keys of users need to be made available to other participants somehow.

The size of an Identity-Based signature (IBS) is an important factor when selecting a cryptographic system. In this paper, we adopt the IBS-1 scheme [22] which can be considered an identity-based counterpart of the well-known Boneh-Lynn-Shacham (BLS) signature scheme [23]. It relies on the advantages of elliptic curve cryptography and bilinear pairing. By using just only one x-coordinate, instead of the two coordinates required by other standard algorithm, such as the Elliptic Curve Digital Signature Algorithm (ECDSA) [24], the IBS-1 signature is about half the size of the one produced by ECDSA. In Table 1 we show a comparison between ECDSA and IBS-1 signature size considering a security level of 80 bits.

Table 1. IBS-1 and ECDSA signature size comparison, considering an MNT (Miyaji, Nakabayashi and Takano) elliptic curve over a prime field with 80 bits security level.

Signature scheme	Signature size	Public key size	Private key size
ECDSA	320	160	160
IBS-1	160	160	160

Table 1. IBS-1 and ECDSA signature size comparison, considering an MNT (Miyaji, Nakabayashi and Takano) elliptic curve over a prime field with 80 bits security level.

Signature scheme	Signature size	Public key size	Private key size
ECDSA	320	160	160
IBS-1	160	160	160

3.1. IBS-1 Signature Scheme

In this section we describe the IBS-1 scheme. It consists in a quadruple of probabilistic polynomial time (PPT) algorithms (Setup, KeyGen, Sign, Vrf).

• Setup takes a security parameter $1^k$ as input (here, $1^k$ is the unary notation for the security parameter, i.e., key material is k bits long), and returns the master (signing) key s plus a set of system parameters params that includes the system public key $P_{pub}$;
• KeyGen takes as inputs the master key s and an identity $id\in {\{0,1\}}^{*}$, and returns a secret signature key $S_{id}$;
• Sign takes as inputs the secret signature key $S_{id}$ and a message $m\in {\{0,1\}}^{*}$, and returns the signature σ of m;
• Vrf takes as inputs $P_{pub},id,msg$ and σ. It returns 1 if σ is a valid signature of m related to $id$, and 0 otherwise.

The PKG runs Setup algorithm which defines the elliptic curve $E\left({\mathbb{F}}_q\right)$ to be used, and a generator point $P\in E\left({\mathbb{F}}_q\right)$ of prime order l. It also initializes public system parameters for the intended service.

Algorithm 1 Setup algorithm

Choice of an elliptic curve $E\left({\mathbb{F}}_q\right)$, and a point $P\in E$ of prime order l with $gcd(l,q-1)=1$. - Selection of a point $P\in E\left({\mathbb{F}}_{q^k}\right)$ of order l and definition of the bilinear pairing e Choice of a pseudo-random integer $s\in {\mathbb{Z}}_l^{*}$ as its master key, and computation of its public verification key $P_{pub}=sP$. Publication of $E,e,l,P,P_{pub}$ and of the two hash functions: $$H:{\{0,1\}}^{*}\to \mathbb{G},h:{\{0,1\}}^{*}\to Z_l^{*}$$

The KeyGen algorithm extracts the private keys for a set of registered users. The PKG does the following:

Algorithm 2 KeyGen algorithm

For each binary string $id$ in a suitable finite set: Computation of digests $H\left(id\right)$ and $h\left(id\right)$. Computation of the elements of $\mathbb{G}(+)=\langle P\rangle$: $$S_{id}=sH\left(id\right)$$ (1)

which represent private key corresponding to the identity id.

In the IBS-1 scheme, illustrated in Algorithm 3, the signer $id$ uses its private key $S_{id}$ given by Equation (1) and the public parameters returned by the Setup algorithm in order to compute the signature $(\Sigma ,R)\in \mathbb{G}\times \mathbb{G}$ of message m. The verifier can check the signature due to the knowledge of the signer identifier $id$ and the public parameters returned by the Setup algorithm.

Algorithm 3 IBS-1 signature scheme

Sign: the signer $id$ does the following - Choice of a pseudo-random integer $r\in {\mathbb{Z}}_l^{*}$, and computation of the public element $R=rP$. - Computation of the element of $\mathbb{G}(+)=\langle P\rangle$: $$\Sigma =\frac{S_1\left(id\right)}{r+h\left(m\right)}$$ (2) The couple $(\Sigma ,R)$ represents the signature by user $id$ for message m. Vrf: the verifier does the following - Computation of digests $H\left(id\right)$, $h\left(m\right)$ and point $R+h\left(m\right)P$. - Check of the equality $$e(\Sigma ,R+h\left(m\right)P)=e(H\left(id\right),P_{pub})$$ (3) and acceptance of the signature only if Equation (3) is true.

It the following theorem we verify the correctness of the IBS-1 signature scheme. Substituting the value $S_1\left(id\right)$ given by Equation (1) in the Equation (2) of Σ, from the Bilinearity of e.

Theorem 1. Suppose that no adversaries interfere with the execution of signature scheme. By virtue of Equation (3), the scheme is correct:

$$\begin{array}{c}\hfill e(\Sigma ,R+h\left(m\right)P)=e\left(\frac{sH\left(id\right)}{r+h\left(m\right)},(r+h\left(m\right))P\right)=e(sH\left(id\right),P)=e(H\left(id\right),P_{pub})\end{array}$$

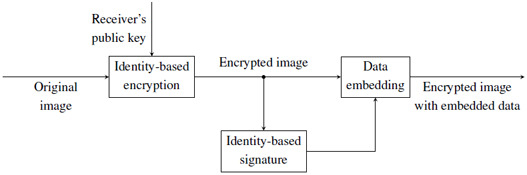
4. Proposal

In this section, the innovative aspects that allow the signature to be embedded into the encrypted image are discussed.

4.1. Tiling with Unequal Patches

Watermarking methods that partition the image into square patches use identical non-overlapping patches of predetermined size. In this work, we used a tiling with square patches of different sizes, in order to take advantage of the different correlation levels in various areas of the image. To keep the complexity of the tiling under control, edges of the (composite) patches are constrained to be multiples of a basic patch of B-by-B pixels. The value of B can be predetermined (e.g., 8 pixels, a value widely used in image compression) or set in accordance with the properties of the specific images considered in an application.

The tessellation is obtained by means of a greedy algorithm that considers basic patches one at a time, in a prefixed order. Basic patches are scanned in row-wise order, starting from the upper left corner. For each basic patch considered, the tessellation algorithm evaluates if the patch should be kept as is, or if it should be integrated in a composite square patch. In our framework, the decision is based on the combination of two functions:

• A quality function $\psi \left(p\right)$ that determines if it is convenient to expand a patch p including its western, southwestern, and southern neighbors. The quality function can be a general measure of the spatial correlation among pixels or of the entropy, or a pixel value prediction method such as, for example, Checkerboard Based Prediction (CBP) [25]. An alternative idea that can be used when the actual embedding function is computationally light is to actually apply it to the patches separately and to the combined patch, comparing the relative gain/loss. Clearly, storing partial results speeds the computation up.
• A penalty function $\xi \left(p\right)$ accounting for constraints that a bigger patch imposes over adjacent patches. Figure 1 shows, for example, that a 3-by-3 patch (labeled as c) constrains the two basic patches labeled a and b to be considered as basic patches only. As penalty function, we used a count of the basic patches that were deprived from the opportunity of being expanded:

  $$\xi \left(p\right)=\#\left(\text{constrained}\text{basic}\text{patches}\right)$$

Figure 1. The 3 × 3 patch c constraints patches a and b to be 1 × 1.

Figure 1. The 3 × 3 patch c constraints patches a and b to be 1 × 1.

The final scoring function $\omega \left(p\right)$ is given by

$$\omega \left(p\right)=\frac{\psi \left(p\right)}{Q+\xi \left(p\right)}$$

where Q is a parameter controlling the weight of the penalty function. Low values for Q will enlarge the impact of small increases of $\xi \left(p\right)$. Within a patch, an efficient embedding algorithm with low distortion and high payload is used. While our system can handle all algorithms that can operate locally (which include the vast majority of embedding algorithms), in our preliminary experiments we used the embedding algorithm based on the Slantlet transform [26]. The slantlet transform has been shown to outperform the Discrete Wavelet Transform (DWT) as far as the compromise between smoothness and localization is concerned, making it a strong candidate for transform-based embedding.

In order to describe the tessellation with sufficient detail to allow reconstruction on the receiving side, information regarding the tessellation should be embedded in the image as well. When a patch $p_i$ is considered, the position of next basic patch in the sequence can obviously be determined, given the size of p. Once the next patch $p_{i+1}$ is determined, its edge size $s_{i+1}$ is embedded as auxiliary information in patch $p_i$. Note that the size of the initial patch is embedded at last using a generic RDH algorithm. It will be extracted as a preliminary operation during recovery. Recovery should proceed in the same order as embedding. Edge sizes will typically be small integers, thus requiring a small number of bits. In addition, a limit can be easily imposed the maximum patch size (e.g., 4) so that the number of bits needed to encode $s_{i+1}$ will be known in advance.

4.2. Using Identity-Based Short Signatures

As discussed in Section 3, the IBS-1 scheme produces much shorter signatures than the standard ECDSA algorithm, making it a strong candidate for a signature that is compact enough to be embedded even in encrypted images.

The algorithmic tools that we use in this work offer a wide range of combinations supporting several usage scenarios. For example, there is no constraint on the algorithm that the image owner may choose in order to encrypt the image: any algorithm can be selected. By contrast, IBS-1 is required for the signing phase. However, to fix the ideas, consider the scenario depicted in Figure 2. The image owner encrypts the image using the identity of the intended receiver. Subsequently, the encrypted image is signed, using an hash of it as usual, and the resulting signature is embedded in the encrypted image. The receiver can verify the signature and decrypt the image. Note that the scenario in Figure 2 assumes that the number of users sending and receiving images is high, thus exacerbating the issues of key distribution and key storage that would have arisen if symmetric cryptography had been used. Otherwise, the latter would have been preferable for encryption, in light of its edge on performance over public-key encryption.

Figure 2. An usage scenario.

Figure 2. An usage scenario.

Figure 3 shows an example image (a), the same image encrypted with IBC (b) and the resulting image after embedding the IBS-1 signature into it. The theoretical specification of a cryptographic system should be complemented by a properly engineered and rigorously verified implementation [27]. We have used the jPair [28] cryptographic library to implement the IBS-1 signature. jPair natively supports some supersingular and ordinary elliptic curves over large prime fields, and implements all the arithmetic required for finite fields and Tate pairings. Its implementation is inspired to [29], that introduced the idea of encapsulated point doubling/addition based on projective coordinate system. Although other libraries exist with similar characteristics (e.g., the reference benchmark C library PBC [30] and its Java port jPBC [31]), jPair is a pure Java implementation with no dependencies on external libraries and a very small memory footprint. It combines fast computation over elliptic curves with the benefits of portability and rapid development coming from the use of Java.

Figure 3. Example: (a) original image; (b) encrypted image; and (c) encrypted image with embedded short signature.

Figure 3. Example: (a) original image; (b) encrypted image; and (c) encrypted image with embedded short signature.

5. Conclusions

In this paper, an architectural framework to address the problem of digitally signing an encrypted image by embedding the signature as the payload of a lossless data hiding algorithm is discussed. Since encrypted images offer less room for embedding that the corresponding unencrypted images, either the embedding capacity should be increased, the size of the payload to de embedded should be reduced, or both. To reduce the size of the signature, and hence the amount of data that should be embedded, a recently proposed signature scheme, IBS-1, has been used. A nonuniform tessellation strategy allows to take advantage of local structure, which depends on the characteristics of the original image as well as on the encryption used. For example, a block cipher in ECB mode as in [17] would preserve much of the local structure of the original image. In ECB mode, however, encrypting a block of a fixed value always yields the same result, increasing the vulnerability to dictionary attacks.

Directions for future work include the study of different usage scenarios, the integration of the proposed ideas in a Signcryption scheme [32,33], and the investigation of strategies aimed at improving the robustness of the proposed framework with respect to image transformations and manipulations.