1. Introduction
As the second largest economy in the world, China is facing serious environmental issues owing to rapid development of economy. From the start of 2003, an uncommon heavy fog and haze weather swept over central and eastern region in China, which drew widespread attention from public [
1,
2]. Since then, the environment has gradually deteriorated. In 2014, the air quality of nearly 90% China’s cities have not met the standards [
3]. Additionally, in accordance with the 2016 Environmental Performance Index, the air quality of China ranked 109th in 178 countries [
4]. Such serious air pollution problems in China not only threaten the health of local people, but also pose great damage to the global air quality [
5]. Thus, the reasons caused environmental problems, and the measures taken to control the pollution in China gain widespread concerns around the world [
6]. Even though a series of measures have been implemented by Chinese government to enhance air quality, such as establishing the national air quality monitoring network, closing down small energy-intensive enterprises with heavy pollution, eliminating backward production capacity, and developing renewable energy, the effects have not been remarkable.
Due to China’s heavy dependence on fossil energy, including coal energy, and petroleum energy, as well as secondary industry, sulfur dioxide (SO
2) is one of the significant air pollutants which emissions amount came to the top at 25.89 million tons in 2006 [
7]. Although Chinese government set series of goals to cut down SO
2 emissions, the volume of SO
2 emissions is still a critical burden for the environment. Therefore, recent years, some literatures researched on the driving forces of SO
2 emissions and environmental Kuznets curve for SO
2 discharge to find solutions for reducing SO
2 discharge. Literatures about factors affecting SO
2 emission can be classified into two categories, direct aspects and indirect aspects. Since atmospheric pollutants are mainly generated from energy consuming, direct forces refer to energy-related causes, while indirect factors imply socio-economic elements which firstly act on energy-related factors and then influence air pollutant emissions. Sinha [
8] researched on the influence of energy intensity and economic development on SO
2 emissions. Yao et al. [
9] employed index decomposition analysis method to analyze the overall industrial scale in the change of SO
2 discharge and found that engineering emission reduction and supervision emission reduction contributed the most to reduce SO
2 emissions, while structure emissions reduction has not shown a remarkable effect. Han et al. [
10] established a new decomposition method combining Grossman decomposition model with logarithmic mean Divisia index (LMDI) method to analyze the factors affecting industrial SO
2 emissions. They found that the scale effect was the significant factors influencing SO
2 emissions. Literatures above all studied on indirect influencing factors on SO
2 discharge, while some studies also researched on direct impact factors. Wang et al. [
11] examined the impacts of treatment technology on SO
2 discharge for industry employing LMDI method. Yang et al. [
12] analyzed the influence of three critical direct elements: energy consumption, energy structure, and treatment technology on SO
2 discharge in China employing LMDI. They found that energy consumption was the primary reason for SO
2 increasing, while the improvement of treatment technology played a significant role in reducing SO
2 emissions.
Empirical studies on environmental Kuznets curve can be retrospected to the work of Grossman and Krueger [
13], who firstly found evidence for the existence of the inverted U-shaped nexus between some contaminant indicators and GDP for 42 countries. Since then, the existence of environmental Kuznets curve hypothesis was proved in carbon dioxide emissions by Holtz-Eakin and Selden [
14], and Stern et al. [
15], in sulfur discharge by Kaufmann et al. [
16] as well as List and Gallet [
17], in four critical atmospheric pollutants by Selden and Song [
18], Harbaugh [
19], and Miah [
20], and in renewable energy by Angeliki and Konstantinos [
21]. Stern and Common [
22] examined the environmental Kuznets curve hypothesis for sulfur discharge employing a separate sample and a global sample of high-income Organization for Economic Cooperation and Development countries, and the findings validated the existence of this hypothesis among these countries. Shen [
23] found a U-shape curve instead of an inverted U-shape curve between sulfur emissions and GDP based on provincial data of China during the period of 1993–2002. The research of Fodha and Zaghdoud [
24] displayed an inverted U-shape curve nexus between sulfur discharge and economic development. Then, series of literatures queried that existing literatures based on income-pollutants environmental Kuznets curve model may provide biased evidence due to the failure to take relevant explanatory variables into consideration [
25]. Therefore, some latest literatures try to study the nexus between income and pollutants by taking energy related variables, urbanization, and technique progress variables into the function. Kohler [
26] found that there existed a long term relationship between environmental quality, per capita energy use and foreign trade in South Africa. Shahbaz et al. [
27] investigated the co-integration relationship and causal relationship among industrialization, electricity consumption, and CO
2 emissions of Bangladesh, and found that environmental Kuznets curve existed between industrial process and CO
2 discharge. Wang et al. [
28] investigated the relationship among economic development, urbanization, and sulfur dioxide discharge employing panel data model based on semi-parametric panel fixed effects regression. The results showed that an inverted U-shape curve existed between economic development and sulfur dioxide discharge. Zhou et al. [
7] verified an inverse N-shape relationship between sulfur discharge and economic development, and proved the positive influence of technical progress on sulfur discharge reduction.
Although environmental Kuznets curve analysis model is widely applied in researching the relationship between economic growth and contaminants, many scholars and policymakers put forward their critiques on the concept of environmental Kuznets curve hypothesis and methodology in previous researches. Firstly, the inverse U-shape environmental Kuznets curve is not applicable for all kinds of pollutants, and only small amount of empirical analysis support an inverse U-shape environmental Kuznets curve for some primary atmospheric contaminants [
19]. Shafik and Bandyopadhyay [
29] examined a panel of 149 countries during the period of 1960–1990, and found that among ten indicators of environmental quality, only two indicators fitted for an environmental Kuznets curve path. Secondly, a large amount of studies on environmental Kuznets curve hypothesis researched cross-sectional data and summarized an exclusive development path for different countries or provinces, which was criticized for the invalidity of cross-sectional technique [
30,
31].
Above all, considering about the shortcomings of existing literatures on researching the relationship between sulfur emissions and socio-economic driving forces, this paper established a multi-variate panel data model for five provinces with the largest sulfur dioxide (SO2) emissions in China taking economic development, fossil fuel energy consumption, energy consuming intensity, and economic structure into consideration spanning the period of 2002–2015. The main contributions of this paper are as follows:
- (1)
Combining economic development, energy consumption, technical advancement, and economic structure together to analyze the contribution of each variable to SO2 emissions. To the best of our knowledge, this paper is the first study in the field of investigating the relationship between sulfur discharge and socio-economic forces to simultaneously explore the contribution of economic growth, energy consumption, technical progress, and economic structure to SO2 emissions using panel data unit root test and panel co-integration theory. Additionally, granger causality test is also employed to investigate the causal relationship between these four data sequences and SO2 emissions.
- (2)
The contribution of economic development, energy consumption, technical advancement, and economic structure to SO2 discharge can be quantitatively analyzed regarding to different provinces. Based on panel data model, cross-sectional technique can be fully exploited, thus, the contribution degree of four variables to SO2 discharge can be quantitatively measured according to five different provinces, and the causal relationship direction among these four variables and SO2 discharge can be obtained with respect to different provinces. Therefore, the policymakers of different provinces can formulate effective and practicable policies to reduce the discharge of SO2 according to the empirical analysis results.
The rest parts of this paper are conducted as below.
Section 2 majors on introducing the methodology used in this paper and the framework of this research.
Section 3 provides the data sources and pre-analysis. The empirical analysis will be carried out in
Section 4.
Section 5 draws the conclusions and provides policy implications.
2. Theoretical Framework and Methodology
2.1. Test for Cross-Sectional Dependence
The establishment of panel data model should start with cross-sectional dependence test which is necessary for choosing appropriate methods for testing unit root. This paper used the Pesaran cross-sectional dependence test for cross-sectional dependence examination [
32]. The original panel data model can be written as:
where
i = 1, 2, …,
N and
t = 1, 2, …,
T,
βit demonstrates a vector of parameters for
K × 1 to be evaluated,
xit indicates a
K × 1 vector of explanatory variables,
αi implies parameters which do not change with provinces and
μit is supposed to be independently and identically distributed. The null and the alternative hypotheses are represented as follow:
where:
The statistic of the Breusch-Pagan [
33] LM test is provided as Equation (5):
where the
means the coefficients estimated by the residuals of the model. Pesaran [
32] improved the LM test by proposing an alternative test regarding to the average value of
calculated by:
Pesaran [
32] certified the advancement of this test in small samples which is suitable for this study.
2.2. Test for Panel Unit Root
Panel unit root test methods employed in previous literatures can generally be classified into two categories. The first category takes cross-sectional independence into consideration, such as Hadrid [
34], Choi [
35], Levin, Lin and Chu (LLC test) [
36], Im, Pesaran and Shin (IPS test) [
37] and some others. The second category considers cross-sectional dependence, including the test methods proposed by Bai and Ng [
38], Moon and Perron [
39], Pesaran [
40], Phillips and Sul [
41], and Smith et al. [
42]. The equation applied to test stationary is listed as Equation (7):
where
i = 1, 2, …,
N is used to represent province;
t = 1, 2, …,
T demonstrates time point;
Xit indicates the explanatory variables containing fixed effects or individual time trend;
ρi means the coefficient for auto-regression; and
εit implies interference term of stable series.
As Equation (7) may be an autocorrelation, higher order differential delay terms were explored by Levin et al. [
36]:
where
pi represents the lags amount in the regression. Im et al. [
37] verified a
t-bar statistic as the average value of the individual ADF statistic as Equation (9):
where
tρi means the individual
t-statistic to test for the original hypothesis.
2.3. Test for Panel Co-Integration
If the variables sequences are confirmed to be stable in the same order, the process should step to panel co-integration test employing Pedroni’s co-integration test method [
43] of which the regression equation can be written as:
where
i implies various provinces,
t indicates different time points,
M represents the number of explanatory variables,
demonstrates the coefficients of explanatory variables,
means the intercept component, and
is the evaluated residual on behalf of the divergence from the long-run.
Pedroni co-integration examination method is made up of two groups. One is based on the within dimension approach including panel v-statistic, panel ρ-statistic, panel PP-statistic and panel ADF-statistic. The other one is based on the between dimension approach consisted of group ρ-statistic, group PP-statistic and group ADF statistic.
2.4. Test for Panel Data Model Form
The primary three forms for panel data model are random effects, fixed effects, and regression models for pooled. The Hausman examination method and the likelihood ratio (LR) examination method are usually employed to test for the proper form of panel data model [
44].
The forms of panel data models contain the constant intercepts and coefficients model, the variable intercepts and invariable coefficients model, and the changed intercepts and coefficients model [
45]. These three forms of panel data models are shown in Equations (11)–(13).
where
i represents the provinces,
t demonstrates the time point,
means the intercept,
indicates coefficient, and
implies the error component.
In order to verify the panel data model form,
F-test will be utilized to decide if the following two null hypotheses should be accepted or rejected by computing the residual sum of squares (RSS) of Equations (11)–(13).
where
F1 is for the
H1 hypothesis of which the slopes are invariable and the intercepts are different,
F2 is for the
H2 hypothesis of which the slopes and the intercepts are all unchanged,
S1,
S2, and
S3 are the residual sum of squares of Equations (11)–(13). Additionally,
N,
T, and
k indicate the amount of provinces, years, and explanatory variables.
Considering the significance level and T > k + 1, if F2 is less than the critical value, then we accept H2 and the panel data model form should be Equation (11), otherwise, it needs to examine hypothesis H1. If F1 is more than the critical value, H1 should be rejected and the panel data model form should be Equation (13), otherwise, it should be Equation (12).
2.5. Test for Causality
Engle and Granger [
46] proposed that if two data sequences are co-integrated, then there exists Granger Causal relationship. At the aim of investigating causality among different data sequences, the Granger causality examination method [
47] is utilized to testify if one data sequence has an impact on another. For Granger causality, if
Y can be forecasted more precisely through using the data of both
X and
Y than using
Y, then we can conclude that the variable
X Granger causes
Y. This method is employed in this paper to identify the causal relationships among different variables:
Equation (18) shows the null hypothesis of the Granger causality examination method, which demonstrates “
X does not Granger-cause
Y”. Equation (19) is used to test if
Y Granger-causes
X.
2.6. Theoretical Framework
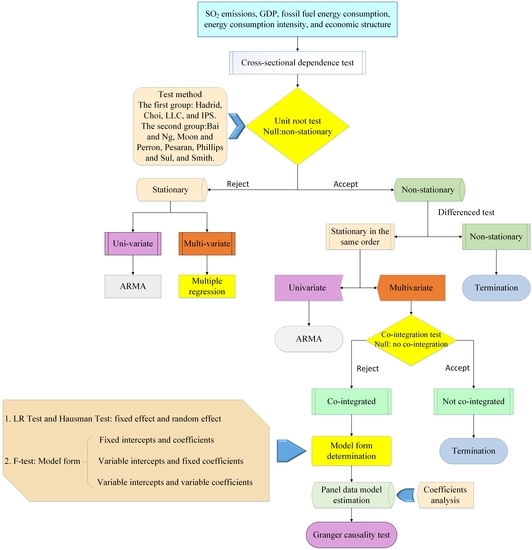
The theoretical framework is demonstrated in
Figure 1. The empirical analysis can be proceeded with following steps.
Step 1: Test for cross-sectional dependence
The empirical analysis will start with cross-sectional dependence test to identify the methods used in unit root test and panel co-integration test.
Step 2: Test for panel unit root
After confirming whether it is necessary to consider cross-sectional dependence, the stable of all variables need to be examined and the methods used in this stage depend on the results of step 1. Only if all variables are stable in the same order, the empirical analysis can proceed to co-integration test.
Step 3: Test for panel co-integration
After verifying all variables are stationary at the same order, Pedroni co-integration examination method will be used for testing whether there exists long-term relationship among SO2 emissions and all independent variables. If not, the panel data model cannot be established, otherwise, we need to determine the form of panel data model.
Step 4: Test for panel data model form
At this step, LR test and Hausman test are used to determine the fixed effect or random effect of panel data model. And then F-test will be employed to judge whether the panel data model is constant intercepts and coefficients model, the variable intercepts and invariable coefficients model, or the changed intercepts and coefficients model. After identifying the model form, the panel data model can be estimated.
Step 5: Test for Granger causal relationship
At the aim of further and better understanding the relationship among SO2 emissions, GDP, fossil fuel energy consumption, energy consumption intensity, and economic structure, Granger causality examination method will be used to explore the nexus among these variables. And the direction of causal nexus can provide policy making references for policy makers.
5. Conclusions and Policy Implications
This paper investigated the relationship among SO2 emissions, GDP, fossil fuel energy consumption, energy consumption intensity, and economic structure of five provinces in China with the highest SO2 emissions employing panel data model approach spanning from 2002 to 2015. Based on panel unit root examination to confirm all variables are stable in the same order, panel co-integration examination to verify all variables are co-integrated in the long-term, and model form determination tests, the panel data model can be estimated and the Granger causality examination can be conducted, which provided strong evidence on the complicated relationships among these variables. Through analyzing the established panel data model, the main conclusions are as follows:
- (1)
Fossil fuel energy consumption makes the greatest contribution to SO2 discharge compared with GDP, energy consumption intensity, and economic structure. And the more the fossil fuel energy consumption, the greater the devotion made by it to SO2 emissions.
- (2)
GDP makes less contribution to SO2 emissions than fossil fuel energy consumption, and the larger the scale of the economy, the greater the contribution made by it to SO2 emissions.
- (3)
The higher the proportion of the secondary industry added value accounted in GDP, the more the devotion made by the economic structure and energy consumption intensity to SO2 emissions.
Through investigating the causal relationship among SO2 emissions, GDP, fossil fuel energy consumption, energy consumption intensity, and economic structure of Hebei, Henan, Inner Mongolia, Shandong, and Shanxi using Granger causality examination method, we can obtain that:
- (1)
A bi-directional causal relationship exists between fossil fuel energy consumption and SO2 emissions among five selected provinces.
- (2)
Uni-directional causal nexus exist running from GDP to SO2 emissions, from energy consumption intensity to SO2 emissions, and from economic structure to SO2 emissions among five chosen provinces.
The empirical analysis of this research can make policy makers better understand the complex relationships between SO2 emissions, GDP, fossil fuel energy consumption, energy consumption intensity, and economic structure of Hebei, Henan, Inner Mongolia, Shandong, and Shanxi. In this way, the significant influencing factors of SO2 discharge can be found, and effective and practicable policies can be formulated according to the contributions of different factors and causality relationships. Therefore, regarding to the above econometric analysis, the following recommendations are put forward:
- (1)
Giving full play to the guiding role of price signals, and improving the price policy for desulfurization. Based on the empirical analysis, it can be found that the consumption of fossil fuel energy makes the greatest contribution to SO2 emissions. However, in the long-run, energy consumption of various provinces in China will still depend on fossil fuel energy to a large extent. Therefore, in the process of using fossil fuel energy, desulfurization equipment is needed to reduce sulfur emissions. Considering about the increase of the cost for enterprises using desulfurization equipment, it is necessary to implement a certain price subsidy policy so that the increased cost due to the use of desulfurization technique can be covered, which can also encourage enterprises to develop desulfurization technology.
- (2)
Formulating a new comprehensive evaluation indicator to measure the regional development level considering economic development and environmental impacts. Currently, GDP is deemed as the significant indicator to evaluate the regional development level, which neglects the environmental impact. Therefore, it is essential to establish a comprehensive evaluation system for measuring regional development level, which can not only consider the level of economic development, but also take the impact of pollutant emissions on the environment in the process of rapid economic development into consideration.
- (3)
Exploring renewable and sustainable energy sources to substitute for fossil fuel energy. Considering the high pollution and limited nature of fossil fuel energy, we should actively exploit other renewable energy to take over the use of fossil resources. Based on regional resources endowment, people in inland areas should energetically develop the use of wind energy and solar energy, such as Hebei, Henan, Inner Mongolia, and Shanxi, while people in coastal areas should positively explore the use of hydropower and tidal energy, such as Shandong.
- (4)
Developing high value added and low pollution emissions industries and reducing the proportion of secondary industry. According to the empirical analysis, we can obtain that the higher the proportion of the secondary industry accounted in GDP, the more the devotion made by the economic structure and energy consumption intensity to SO2 emissions. Therefore, policy makers should draft related policies for economic structure adjustment, which should aims at reducing the proportion of secondary industry and developing high value added and low pollution emissions industries. Additionally, policies related to improve energy using efficiency should be executed.
Based on the above analysis, although the results of this study are inspiring, we also have lots of work needed to be done in the future. The policy effect of reducing SO2 emissions should be quantified and added to the panel data model to analyze the function of policies in decreasing SO2 discharge. Additionally, it is also necessary to analyze the influence of renewable energy and its relevant policies on SO2 emissions. Therefore, policymakers can grasp the policy effect, and propose more effective policies and measures.