Green Project Planning with Realistic Multi-Objective Consideration in Developing Sustainable Port

Abstract

Implementing green projects is critical to achieve the green and sustainable development goal. This paper investigates a green project planning with the realistic consideration of multiple objectives including minimizing the total cost and maximizing the total emission reduction. The realistic multi-objective problem in engineering optimization aims to find a best solution for real-world use instead of finding a set of Pareto-optimal solutions. To handle this problem, we develop a weight sets-based multi-objective evolutionary optimization approach to find the best solution for realistic use. The approach integrates a single-objective evolutionary optimization process, novel solution encoding and decoding heuristics, and a non-dominated sort technique. Based on real-world data from a seaport in China, experiments were conducted to validate the proposed optimization approach. Results show that the proposed approach can effectively solve the real-world multi-objective green project planning problem because the solution found by our approach is one of the Pareto optimal solutions generated by the NSGA-II.

1. Introduction

In the trend of sustainable economy and low-carbon development, it is crucial to achieve the green development goal by implementing various green projects, which results in a very important decision-making problem, green project planning (GPP) problems. The GPP problem is to determine the construction sequence and construction proportion of green projects per year, which is a complex combinatorial optimization problem. Effective GPP is helpful to improve the carbon emission reduction performance.

The port industry is a high energy-consumption industry. Facing ever-increasing market competition as well as energy-saving and emission-reduction requirements, the port industry has a pressing demand to implement various green projects. In real-world GPP in a port, multiple objectives need to be considered simultaneously, including cost and carbon emission reduction performance with the constraint such as time window, budget and time sequence.

This paper thus investigates a GPP problem with realistic multi-objective consideration in developing a sustainable port. The objectives of the investigated problem include maximizing the total CO₂ emission reduction and minimizing the total project construction cost. To solve this problem, a weight sets-based multi-objective evolutionary optimization approach is proposed. This approach integrates a single-objective evolution optimization process, novel solution encoding and decoding heuristics, and a non-dominated sort technique. We validated the effectiveness of this approach by a series of numerical experiments. The experimental data were collected from a representative China coastal port.

This paper contributes the literature by: (1) effectively handling a novel green project planning problem with realistic multi-objective consideration in developing sustainable port; and (2) developing a weight sets-based multi-objective evolutionary optimization approach to solve realistic multi-objective optimization problems.

The rest of this paper is organized as follows. Section 2 reviews the relevant studies in the literature. Section 3 presents the problem description and mathematical model of the investigated GPP problem. In Section 4, a weight sets-based multi-objective evolutionary optimization approach is developed to solve the problem. In Section 5, experimental results to validate the performance of the proposed model are presented. Finally, this paper is summarized and future research direction is suggested in Section 6.

2. Literature Review

The GPP problem investigated in this paper is a special project planning and scheduling problem considering the green project construction and realistic multi-objective. Therefore, the literature review is divided into two kinds of studies. This section first reviews the research related to project planning and scheduling, and then reviews multi-objective optimization techniques to solve this kind of problem.

2.1. Previous Studies in Project Planning and Scheduling

Project planning and scheduling problems have been studied widely in the literature, which involve different industries including surgical scheduling problem [1,2], construction project planning [3,4,5,6], manufacturing resource planning [7,8,9,10,11], enterprise resource planning [12,13], etc. Many papers have been published in this area and some researchers provided related comprehensive review papers [14,15].

Some researchers investigated the project planning and scheduling problems from other perspectives. Bruni et al. [16] addressed the resource constrained project scheduling problem with uncertain activity durations. Tritschler et al. [17] considered a generalization of the resource-constrained project scheduling problem with flexible resource profiles in discrete time periods. Chakrabortty et al. [18] proposed two different integer linear programming (ILP) models to solve resource-constrained project scheduling problem. To better balance environmental issues and economic goals, some researchers investigated the deconstruction project scheduling [15,19], which could have major impacts on the local environment in terms of noise, dust and vibrations. However, few studies have focused on realistic environmental or green objectives in project planning and scheduling problems so far. Huysegoms et al. [20] proposed an attributional life cycle assessment of the secondary environmental impacts of a site remediation. Yu et al. explored the use of project planning methods for integrating sustainability into project management practices of construction engineering projects [21]. A life cycle assessment model, namely the environmental model of construction, was developed by Dong and Ng [3] to help decision-makers assess the environmental performance of building construction projects in Hong Kong from cradle to the end of construction. However, their study only pointed out the importance of environmental factors in project planning and how to evaluate environmental performance in project planning.

As mentioned above, the GPP in a port has not been investigated so far, although studies on various project planning problems have been reported in the literature. In real-world port operations, it is usual that multiple objectives need to be considered simultaneously. It is thus crucial to address a multi-objective GPP problem in a port.

2.2. Multi-Objective Optimization Techniques for Engineering Optimization Problems

To solve multi-objective engineering optimization problems in practice, usually, multiple objectives need to be considered and achieved simultaneously. The weighted sum method [22,23] and the multi-objective evolutionary algorithm [24,25,26,27] are commonly used. However, the weighted sum method needs to determine the weight value of different objectives in advance, but the weight value is usually difficult to determine. There is no a single solution which can simultaneously optimize all objectives when multiple objectives are conflicting. To handle this problem, the concept of Pareto optimality is used to find Pareto optimal solutions [24,28,29]. Genetic algorithm is the most popular meta-heuristic technique for multi-objective problems [26,30]. The fast elitist non-dominated sorting GA (NSGA-II) has attracted more and more attention since NSGA-II was proposed by Deb et al. [31]. NSGA-II has attracted the attention of many researchers and is widely used to solve optimization problems. A multi-objective evolutionary algorithm based on decomposition was proposed by Zhang [32], which is another commonly used method that performs similarly to NSGA-II on multi-objective 0–1 knapsack problems and continuous multi-objective optimization problems. Ke et al. proposed a MOEA/D-ACO algorithm which combine ant colony optimization (ACO) and the multi-objective evolutionary algorithm (EA) based on decomposition (MOEA/D). This algorithm decomposes a multi-objective optimization problem into a number of single-objective optimization problems [33]. However, these methods cannot be directly used to handle the GPP problem investigated in this paper because different chromosome representations and genetic operators are required for different optimization problems. These multi-objective evolutionary algorithms avoid the determination of weights, and instead generate a set of Pareto optimal solutions. However, how to choose the appropriate one from these solutions as the final solution is a major difficulty in practical application.

For real-world multi-objective problems, the precisions of the weights of different objectives are usually not high. There exist limited weight sets in practice. Initiated by this, this paper proposes a novel multi-objective optimization method to handle realistic multi-objective optimization problems, a weight sets-based multi-objective evolutionary optimization approach.

3. Green Project Planning Problems with Multiple Objectives

3.1. Problem Description and Assumptions

To achieve the goal of developing a green port, the port plans to implement $p$ energy-saving and emission reduction projects (green projects). It is important to plan the construction sequence of these green projects since the sequence of project construction affects the construction cost and the effect of emission reduction. These green projects can be classified into separable projects and inseparable projects. The separable project can be divided into a number of identical unit projects (e.g., replacement of a single lamp). Once a separable project (such as replacement project of energy-saving lamps) is started, the completed unit projects in each year will generate the corresponding benefit in the next year. Inseparable projects are continuous projects and only begin to generate benefits in the next year after the whole project is completed. These projects are usually large-scale projects (e.g., the transformation of energy-saving processes for bulk mining operations) and require more capital investment. Each project’s construction is not allowed to stop before it is completed.

Some projects are independent and do not affect each other. These projects can be carried out at the same time. Other projects must satisfy specified precedence constraints. That is, some projects can only be started after their preceding projects are completed. The cost of each project and the benefits achieved are different, and the actual cost of a project is related to the duration of the project construction. The longer is the duration, the higher is the cost. In addition, the construction of a project is also limited by the construction time, budget, and mandatory CO₂ emission reductions.

In accordance with the construction reality of green projects, project planning issues need to consider multiple objectives, including maximizing the total CO₂ emission reduction and minimizing the total project construction cost. The total CO₂ emission reduction is the sum of the CO₂ emission reductions for all projects during construction period. The project construction cost is the sum of the construction cost for all projects. The problem needs to determine: (1) the start and completion time of each project; and (2) the proportion of each project’s annual construction.

3.2. Notations

The important notations used in formulating the mathematical model of the GPP problem are classified into four categories, namely indices, parameters, decision variables and intermediate variables, which are listed below.

Indices

$p$	green project, $p\in \left\{1,2,\dots ,P\right\}$
$t$	year, $t\in \left\{1,2,\dots ,T\right\}$

Parameters

$A_p$	number of unit projects included in green project $p$
$N_p$	maximum allowable construction period for green project $p$
$S_p$	annual CO2 emission reduction of a unit project of project $p$
$B_p$	maximal construct cost of project $p$
$F_p$	cost saving led by one-year construction time reduction of green project $p$
$M_p$	1 if green project $p$ is an inseparable project, otherwise it is 0
$G_t$	construction budget for green projects in year $t$
$G$	total construction budget for all green projects
$D_t$	CO2 emission reduction goal in year $t$
$D$	total CO2 emission reduction goal during the $T$ year construction period

Decision variables

$X_{tp}$	1 if the construction of project $p$ is started in year $t$, otherwise it is 0
$Z_{tp}$	1 if the construction of project $p$ is finished in year $t$, otherwise it is 0
$Y_{tp}$	construction ratio of project $p$ in year $t$

Intermediate variables

$C_{tp}$	cumulative proportion of project p completed before year $t$
$S_{tp}$	1 if the construction of whole project $p$ is finished before year $t$, otherwise it is 0
$B_p^{\prime }$	actual cost incurred by project $p$ during construction, which is related to the time spent on the construction of project $p$. The longer the construction time, the higher the cost.

3.3. Constraints

The real-world GPP problem is subject to the following constraints.

The budget constraints for the $t\mathrm{th}$ year and the entire construction period must be satisfied, respectively.

$${\displaystyle \sum _{p=1}^P\left(Y_{tp}\cdot B_p^{\prime }\right)}\le G_t\forall t$$

(1)

$${\displaystyle \sum _{t=1}^T{\displaystyle \sum _{p=1}^P\left(Y_{tp}\cdot B_p^{\prime }\right)}}\le G$$

(2)

The amount of total CO₂ emission reduction during the entire construction period must exceed the reduction goal.

$${\displaystyle \sum _{t=1}^T{\displaystyle \sum _{p=1}^P\left[\left(1-M_p\right)\cdot C_{tp}\cdot S_p+M_p\cdot S_{tp}\cdot S_p\right]}}\ge D$$

(3)

The duration of the construction of the project cannot exceed $N_p$.

$${\displaystyle \sum _{t=1}^T\left(t\cdot Z_{tp}\right)}-{\displaystyle \sum _{t=1}^T\left(t\cdot X_{tp}\right)\le N_p}\forall p$$

(4)

The project precedence must be satisfied.

$$C_{t{p}^{\prime }}\le C_{tp}\forall t,p\to p^{\prime }$$

(5)

For inseparable project $p$ and $p^{\prime }$, the construction of project $p^{\prime }$ can only be started after its preceding project is completed. The actual cost of project $p$, which is related to the construction time, is calculated by Equation (7).

$${\displaystyle \sum _{t=1}^T\left(t\cdot X_{t{p}^{\prime }}\right)}\ge {\displaystyle \sum _{t=1}^T\left(t\cdot Z_{tp}\cdot M_p\right)}\forall p\to p^{\prime }$$

(6)

$$B_p^{\prime }=B_p-F_p\cdot \left[N_p-\left({\displaystyle \sum _{t=1}^T\left(t\cdot Z_{tp}\right)-}{\displaystyle \sum _{t=1}^T\left(t\cdot X_{tp}\right)}\right)\right]\forall p$$

(7)

The cumulative construction ratio of project $p$ in the first $t^{\prime }-1$ years is given below.

$$C_{t^{\prime }p}={\displaystyle \sum _{t=1}^{t^{\prime }-1}{Y}_{tp}}\forall t^{\prime }$$

(8)

The completion ratio of project $p$ in the first $t^{\prime }-1$ years is calculated below. The ratio is 1 if project $p$ is finished in the first $t^{\prime }-1$ years, and it is 0 otherwise.

$$S_{tp}=0\forall C_{tp}<1$$

(9)

$$S_{tp}=1\forall C_{tp}=1$$

(10)

Once project $p$ starts, it cannot be stopped, and the cost must be generated year by year until the project is completed.

$$Y_{t^{\prime }p}>0\forall p,{\displaystyle \sum _{t=1}^T\left(t\cdot X_{tp}\right)}<t^{\prime }<{\displaystyle \sum _{t=1}^T\left(t\cdot Z_{tp}\right)}$$

(11)

Constraints (12)–(18) stipulate the non-negativity and integrality constraint of decision variables.

$$Y_{t^{\prime }p}=0\forall p,t^{\prime }\le {\displaystyle \sum _{t=1}^T\left(t\cdot X_{tp}\right)},t^{\prime }\ge {\displaystyle \sum _{t=1}^T\left(t\cdot Z_{tp}\right)}$$

(12)

$$Y_{tp}\in \left\{\frac{1}{A_p},\frac{2}{A_p},\dots ,1\right\}\forall t,M_P=0$$

(13)

$$Y_{tp}\in \left[0,1\right]\forall t,M_P=1$$

(14)

$${\displaystyle \sum _{t=1}^T{X}_{tp}}=1\forall p$$

(15)

$${\displaystyle \sum _{t=1}^T{Z}_{tp}}=1\forall p$$

(16)

$${\displaystyle \sum _{t=1}^T{Y}_{tp}}=1\forall p$$

(17)

$$X_{tp},Z_{tp},S_{tp},M_p\in \left\{0,1\right\}\forall t,p$$

(18)

3.4. Objective Functions

The investigated GPP problem aims at maximizing the total CO₂ emission reduction and minimizing the total construction cost, expressed as the following two equations:

$$\max f_1={\displaystyle \sum _{t=1}^T{\displaystyle \sum _{p=1}^P\left[\left(1-M_p\right)\cdot C_{tp}\cdot S_p+M_p\cdot S_{tp}\cdot S_p\right]}}$$

(19)

$$\min f_2={\displaystyle \sum _{t=1}^T{\displaystyle \sum _{p=1}^P\left(Y_{tp}\cdot B_p^{\prime }\right)}}$$

(20)

4. Weight Sets-Based Multi-Objective Evolutionary Optimization Approach

This section presents a weight sets-based multi-objective evolutionary optimization approach for the investigated GPP problem in detail.

4.1. Overview

The investigated GPP problem needs to decide the decision variables $X_{tp}$, $Z_{tp}$ and $Y_{tp}$, and the values of variables $X_{tp}$ and $Z_{tp}$ can be determined based on the value of variable $Y_{tp}$. To solve this problem, we thus have to determine the value of decision variable $Y_{tp}$ to achieve the problem objectives.

In real-world GPP, the precisions of the weights for each objective is not high. That is, the number of weight sets in multi-objective GPP problems are limited in practice although there are infinite weight sets in theory. As a result, there is no need to handle real-world multi-objective optimization problems in most engineering applications based on all weight sets. Therefore, this research proposes a simple method to handle the investigated GPP problem. First, generate all possible weight sets according to the precision requirements of real-world GPP. Second, for each weight set, turn the multi-objective problem to a single-objective problem by the weighted sum method, and use the single-objective optimization algorithm to solve this problem. Therefore, we can get many different solutions to single-objective problems with different weight sets. 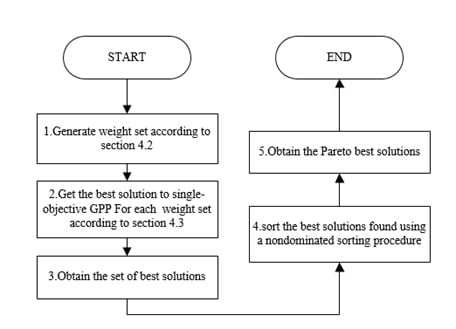Then, we use the non-dominated sorting method [31] to sort these solutions and select out the Pareto best solutions among them. These Pareto optimal solutions are the final solution to the investigated GPP problem. Based on this idea, a weight sets-based multi-objective evolutionary optimization approach for this GPP problem is developed. The flowchart of this approach is shown in Figure 1.

4.2. Setting of Weight Sets

According to the flowchart of the proposed approach shown in Figure 1, the first step of the proposed algorithm is to generate weight sets. We use weight $w_1$ to measure the importance of the port’s environmental benefits during the green project construction, and weight $w_2$ to measure the importance of the cost of the green project construction. It is a common practice that the importance of the construction cost is slightly greater than the environmental benefit during the project construction period. This paper thus sets $w_1+w_2=1$ and that $w_2$ starts from 0.15 to 0.35 and increases by 0.01. Therefore, there are 21 weight combinations. The investigated multi-objective problem can be turned to 21 single-objective optimization problems. If the weights’ precision requirements are higher, we can set a smaller step size. However, the smaller step size will increase the number of single-objective problems to be solved. The setting of the step size is an effective way to balance the solution accuracy with the solution time.

4.3. Single-Objective Evolutionary Optimization Process

After weight sets are generated, the second step of the proposed algorithm is to generate the optimal solutions to the single-objective optimization problem corresponding to each set of weights. In this research, the original problem is converted into 21 single-objective problems under different weight combination. Optimal algorithm such as genetic algorithm, ant colony, harmony search, etc. can be used to solve this single-objective problem. This research uses a standard genetic algorithm [34] to perform the single-objective optimization process in Step 2 of Figure 1. The roulette wheel operator was applied to select the population. To adapt the proposed presentation, two point crossover operator and bit-flip mutation operator [35] were adopted. To adapt the problem features, this study proposes a specific encoding and decoding method, which is described in detail below.

4.3.1. Encoding

The first step of genetic algorithm is to determine the encoding mechanism. The investigated problem needs to determine the values of three decision variables. The three variables involve integer variable and real variables, which leads to a very large solution space. However, it is difficult to encode these different types of variables in one solution individual. From another perspective, if the processing sequence of different projects is given, we can determine the values of three decision variables by a decoding procedure described in Section 4.3.2. This research thus uses an order-based representation to handle this problem. According to this representation, each individual represents the sequence of the project construction. Figure 2 shows an example of this individual representation, which indicates the sequence of eight projects (Projects 1–8) to be implemented in turn. However, this representation cannot determine the values of the three decision variables directly, which are determined by the decoding procedure in Section 4.3.2.

4.3.2. Decoding

The decoding procedure is used to find the values of decision variables for each solution individual. The value of the decision variable $Y_{tp}$ can be obtained by decoding the individual through the heuristic rule. Then, the objective value of the single-objective problem can be calculated as the fitness value under the different weight sets. The heuristic rules for decoding are as follows:

Step 1

Initialize parameters: index $t=1$, construction period $T$, population size, population, annual budget $RB(t)$ and project construction cost $Cost(p)$.

Step 2

Choose the project $p$ with the highest priority that is not finished construction.

Step 3

In the case of not exceeding the budget for year $t$, maximize the construction percentage of project $p$, and this percentage is denoted as $Y_{tp}$.

Step 4

Update the remaining budget $RB(t)$ for year $t$.

Step 5

Select the project $p1$ that has the highest priority next to project p that is not finished construction. Let $p=p1$.

Step 6

Go to Step 3, if the remaining budget is sufficient for the construction of a unit project $p$ equivalent to $RB(t)\ge Cost(p)$.

Step 7

Set $t=t+1$. Stop if $t>T$ or all of the projects have been completed, else go to Step 2.

Take the individual in Figure 2 as an example; with this decoding procedure, the individual can be decoded as shown in Figure 3. This figure shows that Projects 1–3 are carried out separately in the first year, and the construction ratios are: 100%, 100%, and 50%, respectively. In the second year, Projects 3 and 4 are carried out, and the construction ratios are, respectively, 50%, 10%, and 50%. In the third year, Projects 4 and 5 are implemented, and the construction ratios are 90% and 10%. respectively. In the fourth year, Projects 5–7 are implemented. The construction ratios are 90%, 100%, and 50%, respectively. In the fifth year, Projects 7 and 8 are implemented and the construction ratios are 50% and 100%, respectively.

5. Numerical Experiments and Analyses

To investigate the performance of the proposed optimization approach, a series of numerical experiments were conducted based on the real-world data. This section highlights one experiment in detail due to the page limit.

5.1. Experimental Data and Settings

The data used in experiments were collected from a representative coastal port, which is one of the most convenient and economical outlets in the central and western regions of China. There are eight green projects to be implemented in this port. The relevant information for each green project is shown in

Table 1. Project-related information.

Project No.	Unit Numbers	Unit Cost (Thousand Yuan)	CO2 Emission Reduction (ton)	Mp	Fp (Thousand Yuan)
1	17	6200	1484	0	620
2	1040	2.59	0.5	1	0.26
3	38	180	25	1	18
4	2	500	9	1	50
5	1	18,950	3142	0	1895
6	23	5400	301	0	540
7	10	300	101	1	30
8	4	1320	2723	0	132

. The Column 2 of the table shows the number of unit projects corresponding to each separable project (each project consists of one or more identical unit projects). Columns 3 and 4of the table show the cost of a unit project and the amount of CO₂ emission reduction after the completion of the project construction respectively. Columns 5–7 of the table indicate whether the project is separable (denoted by M_p, where 1 is separable and 0 is inseparable), the maximum construction period of the project, and the cost saving by decreasing one year construction of a unit project (denoted by F_p), respectively. The construction period was five consecutive years i. During the construction period, the annual budget is set at 58 million yuan and the total budget is 290 million yuan.

The experiments were carried out on a laptop with Intel Core i3-3110M CPU @2.4GHz and 4 GB RAM using MATLAB R2014a. The results generated by the proposed approach are obtained based on the following settings: the population size of genetic processes was 100, and the maximum number of generation was 500. The crossover probability and the mutation probability are 0.6 and 0.01 respectively.

5.2. Experimental Results and Comparison

The problem is solved by the weight sets-based multi-objective evolutionary optimization approach. We can obtain a set of single-objective optimal solutions to each weight set-based single-objective optimization problem. The solutions in the first front of non-dominated sorting are the final solutions to the problem. The experimental results show that only two solutions can be found by solving this problem as 21 single objective optimization problems. In

Table 2. The solution set of the 21 single objective optimization problems.

Solution No.	Project Sequence								Objective 1	Objective 2
1	8	1	7	2	3	6	5	4	162,807	33,169
2	8	1	7	2	3	6	4	5	162,807	33,169

, Column 2 presents the optimal project construction sequence under the corresponding weight combination, while Column 3 presents the objective function value of the solution for the two objectives. In fact, the two solutions obtain the same results after decoding, so the step of non-dominated sorting for each single-objective optimal solution is omitted. We use the heuristic rules in Section 4.3.2 for decoding, and the resulting values for the three decision variables can be draw in Figure 4. The abscissa represents the time and the ordinate represents the project number, the number in the box is the construction ratio. For example, the construction of Project 1 is started in the first year, so that $X_{11}=1$. The construction of Project 3 is started and finished in second year, so that $X_{23}=1$, $Z_{23}=1$ and $Y_{23}=1$.

To verify the validity of the proposed approach, NSGA-II was used to directly solve the same problem and the Pareto front was found as the final solution. Through calculations, we find that the solution number of Pareto frontier is 66 (see

Table A1. The results of Experiment 2.

Solution No.	Project Sequence								Objective 1	Objective 2
1	8	7	4	1	6	5	2	3	160,079	33,117
2	8	7	4	1	6	5	3	2	160,079	33,117
3	8	7	3	1	4	2	6	5	163,048	35,640
4	8	7	3	1	2	6	4	5	163,398	35,744
5	8	7	3	1	2	6	5	4	163,398	35,744
6	8	7	1	4	6	5	2	3	160,079	33,117
7	8	7	1	4	6	5	3	2	160,079	33,117
8	8	7	1	2	3	6	5	4	162,811	33,221
9	8	7	1	2	3	6	4	5	162,811	33,221
10	8	4	7	1	6	5	2	3	160,079	33,117
11	8	4	7	1	6	5	3	2	160,079	33,117
12	8	4	1	7	6	5	2	3	160,079	33,117
13	8	4	1	7	6	5	3	2	160,079	33,117
14	8	3	7	1	4	2	6	5	163,048	35,640
15	8	3	7	1	2	6	4	5	163,398	35,744
16	8	3	7	1	2	6	5	4	163,398	35,744
17	8	1	4	7	6	5	2	3	160,079	33,117
18	8	1	4	7	6	5	3	2	160,079	33,117
19	8	1	7	4	6	5	2	3	160,079	33,117
20	8	1	7	4	6	5	3	2	160,079	33,117
21	8	1	7	2	3	6	5	4	162,807	33,169
22	8	1	7	2	3	6	4	5	162,807	33,169
23	7	8	4	1	6	5	2	3	160,079	33,117
24	7	8	4	1	6	5	3	2	160,079	33,117
25	7	8	3	1	4	2	6	5	163,048	35,640
26	7	8	3	1	2	6	4	5	163,398	35,744
27	7	8	3	1	2	6	5	4	163,398	35,744
28	7	8	1	4	6	5	2	3	160,079	33,117
29	7	8	1	4	6	5	3	2	160,079	33,117
30	7	8	1	2	3	6	5	4	162,811	33,221
31	7	8	1	2	3	6	4	5	162,811	33,221
32	7	4	8	1	6	5	2	3	160,079	33,117
33	7	4	8	1	6	5	3	2	160,079	33,117
34	7	4	1	8	6	5	2	3	160,079	33,117
35	7	4	1	8	6	5	3	2	160,079	33,117
36	7	3	8	1	4	2	6	5	163,048	35,640
37	7	3	8	1	2	6	4	5	163,398	35,744
38	7	3	8	1	2	6	5	4	163,398	35,744
39	7	1	4	8	6	5	2	3	160,079	33,117
40	7	1	4	8	6	5	3	2	160,079	33,117
41	7	1	8	4	6	5	2	3	160,079	33,117
42	7	1	8	4	6	5	3	2	160,079	33,117
43	4	7	8	1	6	5	2	3	160,079	33,117
44	4	7	8	1	6	5	3	2	160,079	33,117
45	4	7	1	8	6	5	2	3	160,079	33,117
46	4	7	1	8	6	5	3	2	160,079	33,117
47	4	8	7	1	6	5	2	3	160,079	33,117
48	4	8	7	1	6	5	3	2	160,079	33,117
49	4	8	1	7	6	5	2	3	160,079	33,117
50	4	8	1	7	6	5	3	2	160,079	33,117
51	4	1	8	7	6	5	2	3	160,079	33,117
52	4	1	8	7	6	5	3	2	160,079	33,117
53	3	7	8	1	4	2	6	5	163,048	35,640
54	3	7	8	1	2	6	4	5	163,398	35,744
55	3	7	8	1	2	6	5	4	163,398	35,744
56	3	8	7	1	4	2	6	5	163,048	35,640
57	3	8	7	1	2	6	4	5	163,398	35,744
58	3	8	7	1	2	6	5	4	163,398	35,744
59	1	4	7	8	6	5	2	3	160,079	33,117
60	1	4	7	8	6	5	3	2	160,079	33,117
61	1	4	8	7	6	5	2	3	160,079	33,117
62	1	4	8	7	6	5	3	2	160,079	33,117
63	1	8	4	7	6	5	2	3	160,079	33,117
64	1	8	4	7	6	5	3	2	160,079	33,117
65	1	8	7	4	6	5	2	3	160,079	33,117
66	1	8	7	4	6	5	3	2	160,079	33,117

in Appendix A), but there are multiple construction sequences for the same construction plan, such as the decoding schemes of Individuals 1 and 2 are the same. Therefore, after the merger of the same decoding scheme, there are only five different construction plans after decoding. For the specific construction scheme, see Figure A1, Figure A2, Figure A3, Figure A4 and Figure A5 in Appendix A.

By comparing the results obtained by the two methods, the solution found by our method is one of the Pareto optimal solutions generated by the NSGA-II. It is found that the conversion of multiple problems to single-objective problem solving under a given combination of weights can simplify the multi-objective optimum-seeking process very well, and obtain the solution in the Pareto optimal front, and avoids the complex process of making decisions in many Pareto optimal solutions.

6. Conclusions

This study investigated a multi-objective GPP problem faced by a port. The mathematical model for the investigated problem has been established, which considers two objectives: minimizing the total cost and maximizing the total emission reduction. A weight sets-based multi-objective evolutionary optimization approach was developed to solve the problem investigated, in which a single-objective evolution optimization process was proposed to seek the best solutions for each weighted sum single-objective problem. A novel individual representation and decoding heuristic rule were presented to handle the investigated problem. The effectiveness of the proposed optimization model was validated by using real data from a port. The experimental results demonstrate that the proposed approach could handle the investigated problem effectively.

The proposed optimization approach provides a new idea to handle multi-objective optimization problems in real-world engineering applications. This approach can easily be extended to handle large-scale and complex multi-objective optimization problems better than traditional multi-objective evolutionary algorithms. The proposed approach uses a decomposition mechanism to find possible best solutions based on realistic weight sets. Its optimum-seeking process can be implemented in parallel. Comparing to commonly used multi-objective optimization approach such as NSGA-II, the proposed approach can largely reduce the optimum-seeking time, but does not decrease the optimization performance.

The approach proposed in this research is helpful for real-world practitioners to make realistic multi-objective optimization decisions in various engineering contexts. Comparing with traditional multi-objective optimization techniques, the proposed approach is more efficient and easier-to-use, which can be widely used to solve various real-world multi-objective optimization problems. Future research will apply this method to solve other project planning problems in different areas. It is also worthwhile to consider the performance and effectiveness of the method under different problem sizes, compared to the Pareto-optimization-based multi-objective algorithms. Another promising direction is to compare the proposed approach with other swarm or firefly algorithm [36] based multi-objective optimization algorithms.