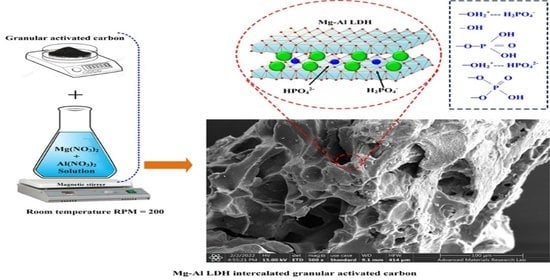
3.1. Characterization of AC/MgAl-LDH Composite Adsorbents
The physicochemical properties of the prepared AC/MgAl LDH composites adsorbents are listed in
Table 3. The elemental compositions of AC/MgAl LDH composites were estimated by X-ray fluorescence spectroscopy (XRF). The obtained results indicate that XRF elemental composition values are well matched with theoretical values. Morphology of the AC/MgAl LDH composites was analyzed using FESEM-EDS analysis, and the corresponding images and EDS spectrum were presented in
Figure 1.
Figure 1a shows FESEM image of raw AC, it can be seen that raw AC contains high porous nature with a wide pore radius size and the EDS mapping confirms the carbon as the main composition with a little amount of Si. As shown in
Figure 1b, AC/MgAl-1 displayed a rough surface with irregular shape particles, while AC/MgAl-2 and AC/MgAl-3 showed a smooth surface covered by spherical particles (see
Figure 1c,d). Furthermore, the EDS spectrum of all the AC/MgAl LDH composites presented carbon, Mg, Al, and oxygen elementals as illustrated in
Figure 1b–d. The EDS analysis results confirm the successful incorporation of (Mg + Al) elements into AC matrices and which is further confirmed by XRD analysis.
The prepared AC/MgAl LDH composite’s surface area, pore volume, and pore radius were calculated using the N
2 adsorption/desorption method.
Figure 2 shows the N
2 adsorption/desorption isotherms of raw AC, AC/MgAl-1, AC/MgAl-2, and AC/MgAl-3 LDH composites. According to the International Union of Pure and Applied Chemistry (IUPAC) classification, raw AC and AC/MgAl composites presented type II isotherm with microporous nature [
44], whereas high (Mg + Al) metal content AC/MgAl-2, and AC/MgAl-3 composites exhibited a typical type IV adsorption isotherm with an H
3 hysteresis loop, demonstrating the typical mesoporous nature materials [
45] which could be probably due to the incorporation Mg and Al into AC matrices thus might expand the porosity of parent AC material.
Table 3 presents the BET surface area, total pore volume of raw AC, AC/MgAl-1, AC/MgAl-2, and AC/MgAl-3 LDH composites. The samples show a gradual decrease in the BET surface area from 829.596 to 584.124 m
2/g while increasing the (Mg + Al) metal loading because a high quantity of Mg/Al-LDH may cause pore blockages in AC, resulting in a decline in the surface area to 584.124 m
2/g. The surface area observations are also corroborated with the pore volumes of the raw AC and AC/MgAl LDH composites.
The FT-IR spectrum of the AC/MgAl LDH composites adsorbents with different (Mg + Al) metal loading is illustrated in
Figure 3. The bands located at 3457 cm
−1 and 1648 cm
−1 are ascribed to -OH stretching and bending vibration [
46]. The peak detected at 2367 cm
−1 is assigned to the stretching vibration of atmospheric CO
2 [
47]. In addition, the peak at 2930 cm
−1 was assigned to C-H stretching vibration of AC material [
48]. However, Mg + Al content composites displayed a sharp peak at 1401 cm
−1 is assigned to the typical nitrate (NO
32−) substances between the LDH interlayers [
49]. In contrast, the absorption peak at 1097 cm
−1 is attributed to the C-O stretching modes of AC [
50]. The peaks between 500 and 800 cm
−1, including 633 and 804 cm
−1 assigned to stretching vibrations of metal oxide bonds such as M-O and O-M-O [
50,
51,
52]. The presence of MgAl-LDH characteristic peak at 1401 cm
−1 in AC/MgAl-LDH composites demonstrates the LDH structure formation in the AC matrixes. The FT-IR results indicate that the surface of the AC/MgAl LDH adsorbents possessed a higher content of oxygen-containing groups, which could significantly enhance the adsorption performance.
XRD patterns of the raw AC, AC/MgAl-1, AC/MgAl-2, and AC/MgAl-3 composites are shown in
Figure 4. The raw AC displayed a sharp diffraction peak at 2θ = 26.75°, corresponding to the (002) plane of the graphitic structure of carbon [
37]. For AC/MgAl LDH composites, in addition to the graphitic carbon, some new diffraction peaks were noticed at 2θ = 11°, 23°, and 34° with (003), (006), and (012) planes attributed to the typical LDH structure of MgAl. These diffraction peaks are associated with the R3m rhombohedral symmetry of the MgAl LDH [
53]. Moreover, the results confirmed that Mg/Al-LDHs were successfully incorporated into the AC matrix.
3.4. Effect of Initial pH on Phosphate Adsorption
For phosphate removal from aqueous media, the pH is one of the most critical parameters as it controls the adsorbent’s surface charge and phosphate dissociation chemistry. The experimental data on the effect of pH on phosphate removal by AC/MgAl-3 are illustrated in
Figure 7. It can be seen from
Figure 7 that phosphate removal declined from 90% to 50% by raising the pH from 2 to 11. Moreover, the removal was almost stable at neutral conditions between pH 6.3 and 8.3. Accordingly, the removal of phosphate ions is favorable in acidic conditions, and the adsorption performance was impaired in the basic media. As a result, the initial solution pH 2.3 is considered an optimum value for removing phosphate ions by AC/MgAl-3. Similar behavior of the effect pH on phosphate removal was reported in the literature [
55]. It was revealed that the results were cross-linked with the acid-base characteristics/charge of the AC/MgAl-3 adsorbent and phosphate ions dissociation in the solution at various pH values. The phosphate ions dissociate with pH and form several forms of phosphate H
3PO
4, H
2PO
4−, HPO
42−, and PO
43− [
56].
The ZPC relates to the mechanism of adsorption and defines the situation in which the density of the electrical charge [
57]. When the pH of the solution is less than the ZPC value, the adsorbent’s surface charge is positive, enabling the anions to be adsorbed. If the pH is higher than the ZPC value, the surface charge of the adsorbent will be negative, allowing higher adsorption of cations [
57]. The ZPC of the AC/MgAl-3 was observed to be around 9.2, as demonstrated in
Figure 8. The influence of pH can be explained as follows, at pH 2.3, phosphate exists mostly as H
2PO
4− and it is getting adsorbed by highly positive adsorbent by the strong electrostatic interactions leading to removal efficiency of 90.2%. At pH 4.1, phosphate ions exist as H
2PO
4− and the magnitude of the positive charge of the adsorbent decreased, and hence the degree of the electrostatic interactions declined by raising the pH to 4.1, which in turn resulted in decreased removal efficiency to about 75.3%. At pH 6.3, the surface charge of the adsorbent is decreased, and the phosphate ions exist as a mixture of H
2PO
4− and HPO
42−, but mostly as H
2PO
4−, while at pH 8.3, the magnitude of positive surface charge is expected to decrease and phosphate ions exist mostly as HPO
42− [
58]. Therefore, the removal efficiency decreased to 64.4% and 63.9% at pH 6.3 and 8.3, respectively, due to the reduction in the magnitude of the electrostatic interactions [
56,
59].
At pH 10.2, the adsorbent becomes negatively charged as the ZPC is 9.2, suggesting that no more electrostatic interactions exist in the adsorption process. In contrast, the electrostatic repulsions control the interactions between phosphate ions and the adsorbent surface, and hence the removal decreased to 57.8%. Moreover, increasing the pH to 10.2 implies that the hydroxide ions concentration increases, which in turn competes with phosphate ions on the active adsorption sites, and hence the overall removal efficiency decreased. Further increasing the pH to 12.1 will increase the magnitude of electrostatic repulsions and the concentration of hydroxide ions, and hence the removal is decreased to 53.4%. It is worth mentioning that still, more than 53% removal is achievable at very basic conditions, which is attributed to the affinity of MgAl LDH toward phosphate ions.
3.5. Adsorption Isotherm
Figure 9 depicts the phosphate adsorption isotherms on AC/MgAl-3 at room temperature and at initial concentrations ranging from 20 to 1000 mg/L. The generated isotherm curves were non-linearly optimized using the Excel solver. It is clear that when the initial concentration of the phosphate increases, the phosphate adsorption capacity increases rapidly before gently reaching a plateau.
The model’s parameters and statistical analysis of each fitted model are presented in
Table 4, and the nonlinear fitting plots of the tested isotherms are illustrated in
Figure 9. According to
Figure 9, the Sips model provides the most accurate description of the experimental data. This is confirmed by the highest
R2 (0.969) and the lowest
SSE (1643) values. However, the values of
R2 and
SSE obtained for the Langmuir model are slightly better than the Freundlich model (see
Table 4). Accordingly, the adsorption process of phosphate ions onto AC/MgAl-3 is controlled by both heterogeneously and homogeneously distributed binding sites, implying that monolayer and multilayer adsorption processes occurred in the removal process.
The Freundlich coefficient
nF is greater than 1, indicating that AC/MgAl-3 effectively removes phosphate ions. The number 1/
ns in the sips model indicates the heterogeneity of the AC/MgAl-3 active sites. If 1/
ns is equal to or near 1, the adsorption site is homogeneous, but if it is significantly more than 1, the adsorption site will be heterogeneous. The 1/
ns value observed in this study is less than 1, showing that AC/MgAl-3 adsorption sites towards phosphate are more homogenous, confirming the
R2 and
SSE values. The experimental maximum adsorption capacity for phosphate onto AC/MgAl-3 was 209.8 mg/g, while the Langmuir adsorption capacity was found to be 337.2 mg/g. Both capacities were considered among the best for phosphate ions removal by different LDHs listed in
Table 5. The
RL values in the Langmuir model were between 0.28 and 0.95, indicating that this adsorption process is favorable. Accordingly, the AC/MgAl composite could be a promising adsorbent of phosphate in real wastewater treatment.
3.6. Kinetics
Figure 10 illustrates the adsorption kinetics of phosphate ions onto AC/MgAl-3. As depicted in
Figure 10, the rate of phosphate adsorption was initially rapid (in the first 60 min) due to the availability of vacant sites and the high concentration gradient between the adsorbent surface and the bulk solution. In this period, more than 50% of the phosphate was removed. Next, the removal rate has decreased between 60 and 1000 min, in which the adsorption occurs in the microporous and mesoporous structure of the adsorbent. Finally, after 1000 min, the adsorbent is saturated with phosphate ions, and equilibrium has been achieved, hence there are no major changes in the adsorption capacity.
The results of adsorption kinetics are consistent with previous investigations of phosphate removal by LDHs [
10,
65]. Perhaps the electrostatic interaction between the positively charged metal oxide surfaces and the negatively charged phosphate ions is responsible for the initial high rate of adsorption in this experiment. To further investigate the nature of the removal mechanism, the pseudo-first order, pseudo-second order, Elovich, and intra-particle diffusion kinetic models were applied. The best trend line fits the linearized models, and
R2 values are demonstrated in
Figure 11, while
Table 6 represents the correlation factor and the obtained model’s constants.
The interpretation of these models confirmed that the adsorption of phosphate onto AC/MgAl-3 follows the pseudo-second-order kinetics as observed from Regression coefficient values
R2 = 0.9996 as shown in
Figure 11b. The compliance with the pseudo-second-order model suggests a chemisorption process between phosphate and the LDH structure. In contrast, the pseudo-first order was not in compliance with the kinetic as confirmed from
Figure 11a and
R2 value (0.956). The Elovich model is used to describe the highly heterogeneous surfaces. It can be noticed from
Figure 11c and
R2 value (0.983) that the Elovich model has good agreement with the kinetic data. These results imply that the adsorbent surface is heterogeneous, and some information can be extracted from the Elovich constants.
The initial adsorption rate of the Elovich model (
α) was 218,680 mg/g/min indicating the very fast adsorption at the beginning of the adsorption process. Another essential parameter: is the Elovich model intercept term (1/
β ln(
αβ)). This term provides the adsorption amount after 1 min of adsorption (i.e., when ln(t) = zero). For phosphate removal by AC/MgAl-3, this parameter equals 10.4 mg/g. For an adsorption capacity of 16.2 mg/g, about 62.4% occurred after 1 min of adsorption, indicating the very fast kinetics at the beginning of the removal process.
Figure 11d elucidates the single-step intra-particle diffusion. According to the trend line fit and
R2 value (0.853), the single step intra-particle diffusion does not fit the experimental kinetic data. Usually, the intra-particle diffusion model is used to investigate the adsorption limiting step [
56]. By plotting the data
qt versus
SQRT(
t), if the data has a straight line and passes through zero, the intra-particle diffusion is the adsorption limiting step, otherwise, the adsorption limiting step is more than the adsorption limiting step controlling the removal process. As confirmed in
Figure 11d, the kinetic data did not form a straight line and did not pass through zero. Hence, it is known that the intra-particle is not the controlling mechanism.
Moreover, these results also suggest that the boundary layer diffusion controls the adsorption process to some extent. Splitting the intra-particle diffusion data into three segments produces three straight lines, and the result is illustrated in
Figure 12. Step 1 represents the boundary layer diffusion of phosphate ions onto the active vacant adsorption sites on the surface of the adsorbent. This step occurs in the first 30 min and represents about 80.1% of the total adsorption capacity. In step 2, the adsorption took place within the micropores and mesoporous structure of the adsorbent. This step took 570 min to complete and represents about 17% of the total adsorption capacity. In the last step (step 3), phosphate ions get adsorbed in the macropores of the adsorbent until reaching equilibrium. This step is very slow and takes around 600 min to complete. Step 3 is responsible for approximately 2.9% of the total adsorption capacity. The factors of the three-step intra-particle diffusion are tabulated in
Table 7.
3.7. Thermodynamics and Effect of Temperature
The thermodynamic factors, including Δ
H°, Δ
S°, and Δ
G° calculated for phosphate adsorption in a temperature range between 22 and 60 °C are given in
Table 8. The negative values of Δ
G° suggest that the adsorption of phosphate ions by AC/MgAl-3 is a spontaneous and feasible process. The magnitude of the negative value of Δ
G° is increasing with temperature implying an endothermic adsorption process. This is confirmed by the positive value of Δ
H° (7.64 KJ/mol). The negative or positive value of Δ
S° indicates the degree of freedom of pollutant particles at the solid-liquid interface. In our case, the Δ
S° was positive (31.15 J/mol/K), suggesting the increase in phosphate ions’ randomness and degree of freedom at the adsorbent interface [
66]. These results indicate that removing phosphate ions by AC/MgAl-3 is a favorable adsorption process.
Figure 13 illustrates the effect of temperature on phosphate removal by AC/MgAl-3 at four different temperatures 295, 313, 323, and 333 K. According to
Figure 13, the adsorption capacity of phosphate was gradually increased with increasing temperatures. Meanwhile, the adsorption capacity was 16.23 mg/g at 295 K and 18.1 mg/g at 333 K. The increased adsorption capacity with temperature suggests an endothermic adsorption process confirming the thermodynamic analysis results. This trend might be attributed to the fact that rising temperatures increase the mobility of phosphate ions toward the adsorbent surface and internal pores of the adsorbent. Hence, the adsorption capacity was slightly increasing.
3.8. EDS and FT-IR Analysis of AC/MgAl-3 after Phosphate Adsorption
The AC/MgAl-3 composite elemental composition was examined after phosphate adsorption through EDS analysis, and elemental mapping is presented in
Figure 14. The EDS spectrum shows the presence of phosphorous signals in the sample, which confirms the adsorption of phosphate ions onto the AC/MgAl-3 material surface.
FT-IR analysis was carried out on AC/MgAl-3 adsorbent to gain insights into phosphate adsorption mechanisms between adsorbent and adsorbate.
Figure 15 displays the FT-IR spectra of AC/MgAl-3 composite before and after phosphate adsorption. The broad adsorption at 3484 cm
−1 is assigned to –OH stretching vibrations owing to the structural -OH and interlayer water molecules [
27]. It should be noted that the stretching vibration of -OH functional groups shifted from 3484 cm
−1 to 3471 cm
−1, implying the involvement of -OH in the adsorption process. The peak is located at 1635 cm
−1 due to the bending vibration of the water molecules in the LDH interlayer.
The peak at 1387 cm
−1 is assigned to NO
3− in the interlayer [
27,
67]. A strong asymmetry vibration peak of the P-O bond at 1085 cm
−1 indicated that phosphate was strongly adsorbed by metal oxide surface (Mg-O and Al-O) through potentially monodentate and bidentate formation inner-sphere surface complexes. The peaks in the lower wavenumber region (400–800 cm) correspond to M-OH vibrations and O-M-O stretching (where M = Mg and Al) [
30,
68]. These results were well corroborated with the typical character of LDHs, which had some easily exchangeable interlayer anions. The results indicate that several phosphate adsorption mechanisms could be anticipated. The phosphate adsorption mechanism onto the AC/MgAl-3 composites mainly occurred via phosphate ion exchange with the interlayer NO
3−, electrostatic interaction between positively charged metal oxide surfaces with negatively charged phosphate ions, as well as the inner-sphere surface complexation process via ligand exchange.