Stochastic Forecast of the Financial Sustainability of Basic Pension in China
Abstract
:1. Introduction
2. Forecasting Models and Data Assumptions
2.1. Forecasting Models

2.2. Data Assumption
- Initial population data. This paper takes the population data from 2013 as the initial population data.
- Working age. According to the data from China Population & Employment Statistics Yearbook 2014, the educational status of urban employed persons in 2013 was as follows: the proportion of unschooled persons was 0.9%, primary school 9.5%, junior secondary school 39.0%, senior secondary school 24.1%, college 15.0%, university 10.4%, and graduate and higher level 1.0%. Suppose that the urban residents get their jobs when they are 16 years old after receiving primary school education, 17 years old after junior secondary school education, 19 years old after senior secondary school education, 21 years old after college education, 23 years old after university education, and 28 years old after postgraduate and above education. Then, the average working age is calculated from the weighted average of the educational attainment of urban employed persons, and the average working age is about 18.65. Therefore, we suppose that the working age is 19 and everyone may live up to age 100.
- Retirement age. At present, the retirement age in China is 60 for men, 55 for female civil servants, and 50 for female workers. Suppose that the retirement age is 60 for men and 55 for women.
- Percent male births. According to the data from the national statistics bureau, the sex ratio at birth has decreased from 120.56 in 2008 to 115.88 in 2014, or in other words, a decline in the proportion of male births from 54.66% to 53.68%. Keeping the sex ratio at birth in the normal range is one of the key factors for a harmonious society and the normal range declared by the United Nations is 102–107. Therefore, we assume that the sex ratioat birth is 112 during the forecast period, meaning that the percentage of male births is 52.83%.
- Contribution rate. In 2005, the State Council issued a regulation on the establishment of a unified basic old-age insurance system for enterprise employees. According to the regulation, enterprises pay 20% of the sum of taxable salary to form the social pool funds as a basic pension. Then we suppose that the contribution rate of the basic pension is still 20%.
- Coverage rate. The coverage of a basic pension insurance system for urban employees has expanded year by year, increasing from 30.5% in 1990 to 63.23% in 2013. Furthermore, the Chinese government has set a target of universal coverage by 2020. Nevertheless, the coverage rate remains at about 90%, even in developed countries where the endowment insurance system is very sound. Therefore, we suppose that the coverage rate of the basic pension during the forecast period will increase by 1.5% per year and the maximum value is 90%.
- Proportion of urban population. According to data from the National Statistics Bureau, the proportion of the urban population has increased from 17.92% in 1978 to 53.73% in 2013. Population urbanization rate will keep growing in the next few decades. Based on the National Population Development Strategy research report of 2007, we suppose that the urban population grows by 1% per year [26] and the maximum value is 85% (by reference to the current level of urbanization in developed countries).
- Urban employment rate. According to relevant data from the National Statistics Bureau the urban population employment rate has generally remained at about 80% over the past 20 years. Then it is supposed that the employment rate of urban population during the forecast period still remains at 80%.
- Replacement rate. The replacement rate of the basic pension is the proportion of the pension benefit to the pre-retirement salary. It directly influences the living standards of retired people. The average replacement rate of the basic pension for urban workers has gradually decreased from 71.52% in 2000 to 44.62% in 2013. According to the general idea of the pension insurance system in China, the target replacement rate of the basic pension will be 58.5% in the future. However, we must pay attention to the unprecedented pressure of fund paying caused by the population aging; we suppose that the average replacement rate of the basic pension in the future is 50%.
- Return rate. At present, the investment scope of China’s basic pension fund is rigidly limited to depositing in the bank or buying national treasury bonds. These funds are safe to a large degree, but their return rate is very low [27,28]. In order to increase the return and realize the maintenance and increment of value, China’s State Council issued Old-age Insurance Fund Investment Management Regulations on August 23, 2015. Thanks to the reform of the basic pension system, the investment channels of the pension fund will be broadened and thus it will be likely for the return rate of a basic pension fund to increase. As a reference, the investment scope of the National Social Security Fund includes bank deposits, treasuries, securities investment fund, stocks, investment grade corporate bonds, and so on. At the same time, as the most important strategic reserve, the National Social Security Fund has a very high return ratio, more than 8%. Therefore, the return rate of the basic pension is set by reference to that of the National Social Security Fund. In addition, by using the weighted method, the weighted return rate can be obtained by multiplying the proportion of two funds’ capital scale, which is taken as the weight, by the corresponding return rate, as shown in Table 1. Therefore, we suppose that the long-term average return rate is 5%.
| Items | 2010 | 2011 | 2012 | |||
|---|---|---|---|---|---|---|
| Basic Pension Fund | National Council for Social Security Fund | Basic Pension Fund | National Council for Social Security Fund | Basic Pension Fund | National Council for Social Security Fund | |
| Size of fund/billon yuan | 1536.53 | 837.558 | 1949.66 | 838.558 | 2394.13 | 1075.357 |
| Proportion of fund | 0.647 | 0.353 | 0.7 | 0.3 | 0.69 | 0.31 |
| Return rate | 3% | 9.17% | 3% | 8.4% | 3% | 8.29% |
| Weighted return rate | 1.9% | 3.2% | 2.1% | 2.52% | 2.07% | 2.6% |
| Total | 5.1% | 4.62% | 4.67% | |||
3. Model Parameters and Parameters Estimation
3.1. Model Parameters
3.1.1. Population Parameter
| Age | Time Series Estimating Equations | σ | ||
|---|---|---|---|---|
| 0–4 | 3.9940 | 0.95 | 0.5364 | |
| 5–9 | 0.5590 | 0.36 | 0.1627 | |
| 10–14 | 0.4515 | 0.77 | 0.1473 | |
| 15–19 | 0.7570 | 0.62 | 0.1673 | |
| 20–24 | 1.1420 | 0.90 | 0.1199 | |
| 25–29 | 1.2500 | 0.75 | 0.1402 | |
| 30–34 | 1.6310 | 0.50 | 0.2470 | |
| 35–39 | 2.0335 | 0.65 | 0.1952 | |
| 40–44 | 2.7830 | 0.72 | 0.1829 | |
| 45–49 | 4.0885 | 0.60 | 0.3605 | |
| 50–54 | 6.0730 | 0.67 | 0.7285 | |
| 55–59 | 9.7050 | 0.58 | 1.0898 | |
| 60–64 | 16.2840 | 0.76 | 1.8119 | |
| 65–69 | 25.9845 | 0.86 | 1.7188 | |
| 70–74 | 43.6485 | 0.93 | 2.0365 | |
| 75–79 | 69.0750 | 0.87 | 3.9300 | |
| 80–84 | 109.4740 | 0.83 | 9.2841 | |
| 85+ | 178.5780 | 0.60 | 23.2378 |
| Age | Time Series Estimating Equations | |||
|---|---|---|---|---|
| 0–4 | 4.7025 | 0.93 | 0.8299 | |
| 5–9 | 0.3335 | 0.56 | 0.1022 | |
| 10–14 | 0.3420 | 0.48 | 0.1013 | |
| 15–19 | 0.4825 | 0.70 | 0.1322 | |
| 20–24 | 0.6750 | 0.56 | 0.2278 | |
| 25–29 | 0.7790 | 0.85 | 0.1473 | |
| 30–34 | 0.8785 | 0.65 | 0.1571 | |
| 35–39 | 1.0815 | 0.48 | 0.2273 | |
| 40–44 | 1.5280 | 0.74 | 0.2640 | |
| 45–49 | 2.2820 | 0.89 | 0.1853 | |
| 50–54 | 3.5985 | 0.82 | 0.5095 | |
| 55–59 | 5.7470 | 0.69 | 0.6710 | |
| 60–64 | 9.8145 | 0.69 | 1.3659 | |
| 65–69 | 16.8735 | 0.80 | 1.6429 | |
| 70–74 | 29.0745 | 0.80 | 2.5179 | |
| 75–79 | 48.3085 | 0.74 | 3.8012 | |
| 80–84 | 81.5275 | 0.92 | 3.8404 | |
| 85+ | 143.599 | 0.82 | 9.6016 |

| Age | Time Series Estimating Equations | |||
|---|---|---|---|---|
| 15–19 | 5.1195 | 0.27 | 1.5653 | |
| 20–24 | 109.1060 | 0.84 | 11.3101 | |
| 25–29 | 104.0725 | 0.55 | 11.6693 | |
| 30–34 | 41.6465 | 0.52 | 5.6856 | |
| 35–39 | 12.3760 | 0.77 | 2.7875 | |
| 40–44 | 3.5620 | 0.82 | 1.2606 | |
| 45–49 | 1.8340 | 0.79 | 1.0541 |
3.1.2. Wage Parameter
3.2. Parameter Estimation






4. Simulation Results
4.1. Contributions of the Basic Pension

4.2. Expenditures of the Basic Pension

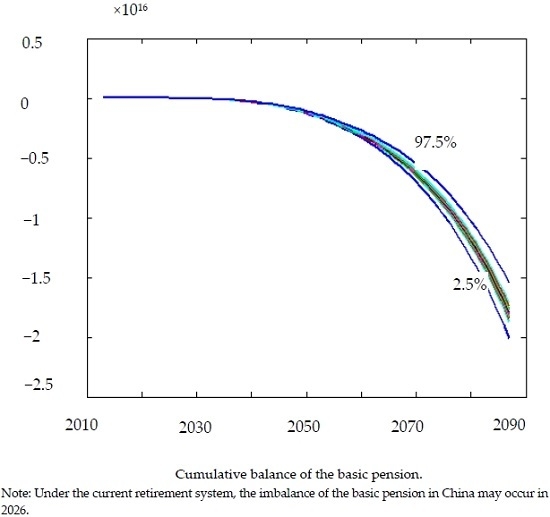
4.3. Cumulative Balance of the Basic Pension

5. Effect of the Delay of Retirement on Pension Sustainability


6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Dorfman, M.; Holzmann, R.; O’Keefe, P.; Wang, D.W.; Sin, Y.; Hinz, R. China’s Pension System : A Vision; World Bank Publications: Washington, DC, USA, 2013. [Google Scholar]
- European Commission. Adequate and Sustainable Pensions, Joint Report of the Commission and the Council; Official Publications of the European Communities: Brussels, Beligum, 2003. [Google Scholar]
- Holzmann, R.; Hinz, R.; von Gersdorff, H.; Gill, I.; Impavido, G.; Musalem, A.R.; Rutkowski, M.; Palacios, R.; Sin, Y.; Subbarao, K.; et al. Old-Age Income Support in the Twenty-first Century: An International Perspective on Pension Systems and Reform; World Bank Publications: Washington, DC, USA, 2005. [Google Scholar]
- Grech, A.G. Assessing the Sustainability of Pension Reforms in Europe; London School of Economics & Political Science: London, UK, 2010. [Google Scholar]
- Pânzaru, C. Some Considerations of Population Dynamics and the Sustainability of Social Security System. Procedia Soc. Behav. Sci. 2015, 183, 68–76. [Google Scholar] [CrossRef]
- Roseveare, D.; Leibfritz, W.; Fore, D.; Wurzel, E. Ageing Populations, Pension Systems and Government Budgets: Simulations for 20 OECD Countries; Economics Department Working Papers No. 168; The Organisation for Economic Co-operation and Development (OECD) iLibrary: Paris, France, 1996. [Google Scholar]
- Petersen, J.H. Recent research on public pension systems. A review. Labour Econ. 1998, 5, 91–108. [Google Scholar] [CrossRef]
- Andersen, T.M. Increasing longevity and social security reforms—A legislative procedure approach. J. Public Econ. 2008, 92, 633–646. [Google Scholar] [CrossRef]
- Heijdra, B.; Romp, W. Retirement, pensions, and ageing. J. Public Econ. 2009, 93, 586–604. [Google Scholar] [CrossRef]
- Kaganovich, M.; Zilcha, I. Pay-as-you-go or funded social security? A general equilibrium comparison. J. Econ. Dyn. Control 2012, 36, 455–467. [Google Scholar] [CrossRef]
- Lee, R.; Tuljapurkar, S. Stochastic Forecasts for Social Security. Front. Econ. Aging 1998, 1, 393–428. [Google Scholar]
- Lee, R.; Yamagata, H. Sustainable Social Security: What Would It Cost? Natl. Tax J. 2003, 56, 27–43. [Google Scholar] [CrossRef]
- Lee, R.; Miller, T.; Anderson, M. Stochastic Infinite Horizon Forecasts for Social Security and Related Studies; NBER Working Paper No. 10917; The National Bureau of Economic Research: Cambridge, MA, USA, 2004. [Google Scholar]
- Social Security Administrate, Office of the Chief Actuary. A Stochastic Model of the Long-Range Financial Status of the OASDI Program; Actuarial Study No. 117; Social Security Administrate, Office of the Chief Actuary: Baltimore, MD, USA, 2004. [Google Scholar]
- World Bank. Averting the Old Age Crisis: Policies to Protect the Old and Promote Growth; World Bank Publications: Washington, DC, USA, 1994. [Google Scholar]
- Williamson, J.; Price, M.; Shen, C. Pension policy in China, Singapore, and South Korea: An assessment of the potential value of the notional defined contribution model. J. Aging Stud. 2012, 26, 79–89. [Google Scholar] [CrossRef]
- Wang, L.; béland, D.; Zhang, S. Pension financing in China: Is there a looming crisis? China Econ. Rev. 2014, 30, 143–154. [Google Scholar] [CrossRef]
- Wang, X.; Ren, W. Studies on the Financial Sustainability of Social Pension System in China. Insur. Stud. 2013, 4, 118–127. [Google Scholar]
- Zhao, B.; Yuan, H. The Analysis of Financial Balance and Sustainability for China’s Basic Pension: Based on the Perspective of Rational Fiscal Payment. Financ. Econ. 2013, 7, 38–46. [Google Scholar]
- Liu, X. Study on the Financing Gap and Sustainability of China’s Pension System. China Ind. Econ. 2014, 9, 25–37. [Google Scholar]
- Zhang, X.; Shi, L. Sustainability of Pension System and Public Debt in An Overlapping Generation Model. Nankai Econ. Stud. 2014, 2, 136–152. [Google Scholar]
- Feng, T.; Gao, X. A Simulation Study on the Sustainability of Rural Pension Based on Parameters Adjusting of Actuarial Models. Chin. J. Manag. Sci. 2015, 9, 153–161. [Google Scholar]
- Ding, S.; Wang, X. A Study on Rural Aging and Sustainable Old-age Security System in China. Econ. Issues China 2012, 2, 52–60. [Google Scholar]
- Feng, T.; Gao, X. The Population Aging Impact on the Sustainability of Rural Pension: An Empirical Study Based on VAR Model. Manag. Rev. 2015, 6, 30–41. [Google Scholar]
- Yu, H.; Zhong, H. On Sustainable Operation of China’s Basic Pension Insurance System: Analysis of Three Simulation Conditions. J. Financ. Econ. 2009, 9, 26–35. [Google Scholar]
- Research Group of National Population Development Strategy. National Population Development Strategy Research. J. China Popul. Res. 2007, 31, 1–10. (In Chinese) [Google Scholar]
- Yang, H. How to Improve the Investment and Operation Mechanism on the Basic Old-age Insurance Fund. J. Cent. Univ. Financ. Econ. 2012, 9, 7–11. [Google Scholar]
- Zhou, P. An Exploration into the Business Model of Basic Pension Insurance Fund Investment and Operation--Based on the Perspective of Three-dimension Value. J. Liaoning Univ. Philos. Soc. Sci. 2015, 1, 99–104. [Google Scholar]
- Jimeno, J.; Rojas, J.; Puente, S. Modelling the impact of aging on social security expenditures. Econ. Model. 2008, 25, 201–224. [Google Scholar] [CrossRef]
- Booth, H.; Tickle, L. Mortality Modelling and Forecasting: A Review of Methods. Ann. Actuar. Sci. 2008, 1–2, 3–43. [Google Scholar]
- Bell, W.R. Comparing and Assessing Time Series Methods for Forecasting Age-specific Fertility and Mortality rates. J. Off. Stat. 1997, 3, 279–303. [Google Scholar]
- Lee, R.; Tuljapurkar, S. Population Forecasting for Fiscal Planning: Issues and Innovations; Burch Working Paper No. B98–05; University of California: Berkeley, CA, USA, 1998. [Google Scholar]
- Lutz, W.; Sanderson, W.C.; Scherbov, S. Expert-based Probabilistic Population Projections. Popul. Dev. Rev. 1998, 24, 139–155. [Google Scholar] [CrossRef]
- Lutz, W.; Sanderson, W.C.; Scherbov, S. The End of World Population Growth. Nature 2001, 412, 543–545. [Google Scholar] [CrossRef] [PubMed]
- Ren, Q.; Hou, D. Stochastic Model for Population Forecast: Based on Leslie Matrix and ARMA Model. Popul. Res. 2011, 2, 28–42. [Google Scholar]
- Keyfitz, N.; Caswell, H. Applied Mathematical Demography, 3rd ed.; Springer: New York, NY, USA, 2005. [Google Scholar]
- Mielczarek, B. Simulation model to forecast the consequences of changes introduced into the 2nd pillar of the Polish pension system. Econ. Model. 2013, 30, 706–714. [Google Scholar] [CrossRef]
- MacDonald, B.; Cairns, A. Three retirement decision models for defined contribution pension plan members: A simulation study. Insur. Math. Econ. 2011, 48, 1–18. [Google Scholar] [CrossRef]
- United Nations. Department of Economic and Social Affairs. World Population Prospects: The 2015 Revision, Key Findings and Advance Tables; Working Paper No. ESA/P/WP.241; United Nations: New York, NY, USA, 2015. [Google Scholar]
- Martín, A. Endogenous retirement and public pension system reform in Spain. Econ. Model. 2010, 27, 336–349. [Google Scholar] [CrossRef]
- Galasso, V. Postponing retirement: The political effect of aging. J. Public Econ. 2008, 92, 2157–2169. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, Y.; Zhao, X. Stochastic Forecast of the Financial Sustainability of Basic Pension in China. Sustainability 2016, 8, 46. https://doi.org/10.3390/su8010046
Tian Y, Zhao X. Stochastic Forecast of the Financial Sustainability of Basic Pension in China. Sustainability. 2016; 8(1):46. https://doi.org/10.3390/su8010046
Chicago/Turabian StyleTian, Yuehong, and Xianglian Zhao. 2016. "Stochastic Forecast of the Financial Sustainability of Basic Pension in China" Sustainability 8, no. 1: 46. https://doi.org/10.3390/su8010046
APA StyleTian, Y., & Zhao, X. (2016). Stochastic Forecast of the Financial Sustainability of Basic Pension in China. Sustainability, 8(1), 46. https://doi.org/10.3390/su8010046