A Spatially Explicit Optimization Model for Agricultural Straw-Based Power Plant Site Selection: A Case Study in Hubei Province, China
Abstract
:1. Introduction
2. Modeling Framework and Methodology
2.1. Spatially Explicit Assessment of Agricultural Straw Availability for Power Generation
2.2. Straw Collection Model Design
- Each CS supplies straw to only the SPP nearest to it;
- When the distance between a certain CS and the SPP nearest to it is less than a certain distance threshold (D1), all the straw collected at this CS will be supplied to the SPP nearest to it;
- When the distance between a certain CS and the SPP nearest to it is greater than a certain distance threshold (D2), the straw collected at the CS will not be supplied to any SPP;
- When the distance between a certain CS and the SPP nearest to it is greater than D1 but less than D2, the amount of straw that the CS can supply to the SPP nearest to it decreases linearly with increasing distance between them.
2.3. Definition and Description of SPPSS Problems
2.3.1. Optimization Objective
2.3.2. Constraints
2.4. Design of the Spatially Explicit Optimization Algorithm
- Algorithm initialization. Based on the antibody-encoding strategy, an initial antibody population containing a certain number of antibodies is randomly generated.
- Cloning. Based on the magnitudes of their affinities, the antibodies in the population are replicated. The higher the affinity of an antibody is, the more times the antibody is replicated.
- Hypermutation. Based on a certain mutation probability, the gene values of the cloned antibodies are altered to generate new antibodies.
- Affinity evaluation. The affinities of the new antibodies generated by mutation are calculated using an affinity evaluation function. The higher the affinity of an antibody is, the better the quality of the schemes corresponding to the antibody.
2.4.1. Antibody Encoding
- 5.
- Determination of candidate sites. To meet the requirements of antibody encoding, candidate sites spaced at the same interval (e.g., 1 km × 1 km) are established in the study area to discretize the continuous geographical space.
- 6.
- CS and candidate site data model. Based on the object-oriented approach, GIS techniques are used to model, store, and process the CSs and candidate sites. As shown in Figure 1, the x- and y-coordinates indicate the spatial locations of the candidate sites, and each site has a unique ID number. To meet the requirements of antibody affinity evaluation, the amount of straw that can be collected by each CS is stored in the form of attribute information.
- 7.
- Antibody model. As shown in Figure 1, each antibody in the AIS corresponds to an optimization scheme for the actual problem. Each gene of an antibody stores a candidate site object. Each gene must have a unique value. The gene length corresponds to the number of SPPs (N) in the optimization scheme.
- 8.
- The terrain, transport network, and natural reserves data required for antibody affinity evaluation are stored and managed using a geodatabase model [56].
2.4.2. Antibody Mutation Algorithm
- Antibody genes are traversed. For any arbitrary gene g, a random number, Pg, is generated. If Pg < Pm, then gene g is mutated.
- For a gene (g) that requires a mutation, a candidate site is randomly selected. If the selected site is not in the current antibody gene set, then the current site in gene g is replaced; otherwise, a new candidate site is selected until the selected candidate site is no longer in the current antibody gene set.
2.4.3. Antibody Affinity Evaluation
3. Case Study
3.1. Description of the Study Area
3.2. Data Acquisition and Preprocessing
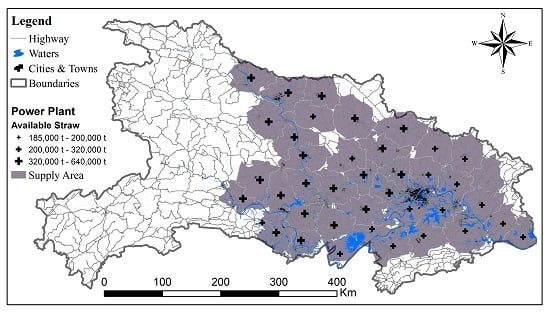
- Estimating the amount of straw available for electricity generation. The spatial distribution and yield of straw available for electricity generation in Hubei Province were estimated based on the ALQG dataset as well as the straw yield estimation model described in Section 2.1 and its parameters (Figure 6). To visualize the data processing process and its results, the estimation results were transformed from vector polygons to raster data consistent with the spatial resolution of the DEM. As shown in Figure 6, agricultural straw is mainly distributed in the plain regions in eastern and central Hubei Province, where river networks and lakes are densely distributed. Through analysis based on the estimation results, the entirety of Hubei Province has an annual straw yield of approximately 34.89 million tons, of which 17.45 million tons can be used for electricity generation.
- Estimating the amount of straw collected by the CSs. Because townships are the lowest-level administrative unit in China, township-level governments are often based in residential areas with a relatively large population and good transport facilities. It is assumed that one CS is set up in each residential area where a township-level government is located. On this basis, the spatial distribution of CSs in the study area was obtained. Because it is difficult to obtain rural road data, the amount of straw that each CS can collect was estimated based on the shortest Euclidean distance. The area within which each CS collects straw was defined using a Voronoi diagram. On this basis, the amount of straw that each CS can collect was calculated using the rasterized straw estimation data and the ArcGIS Desktop spatial statistics tool. Figure 7 shows the spatial distribution of CSs within Hubei Province as well as the area within which each CS collects straw and the amount of straw that each CS can collect.
- Preprocessing candidate sites. Based on the antibody-encoding scheme designed in Section 2.4.2, a set of candidate sites spaced at 1 km ×1 km intervals in the study area was generated. To decrease the optimization space, candidate sites that failed to satisfy distance constraints 1–7 listed in Table 2 were eliminated through GIS spatial overlay analysis and buffer analysis. Thus, a set of candidate sites containing 77,285 candidate sites was obtained.
4. Results and Discussions
5. Conclusions
Supplementary Files
Supplementary File 1Acknowledgments
Author Contributions
Conflicts of Interest
References
- Zhang, L.B.; Liu, Y.Q.; Hao, L. Contributions of open crop straw burning emissions to PM2.5 concentrations in China. Environ. Res. Lett. 2016, 11, 9. [Google Scholar] [CrossRef]
- Zhang, Y.; Zang, G.Q.; Tang, Z.H.; Chen, X.H.; Yu, Y.S. Burning straw, air pollution, and respiratory infections in China. Am. J. Infect. Control 2014, 42, 815. [Google Scholar] [CrossRef] [PubMed]
- Xingang, Z.; Zhongfu, T.; Pingkuo, L. Development goal of 30 gw for China’s biomass power generation: Will it be achieved? Renew. Sustain. Energy Rev. 2013, 25, 310–317. [Google Scholar] [CrossRef]
- Zhang, B.; Zhang, N.; Li, D.; Xu, C. Distribution and use efficiency of straw bio-energy in Jiangsu Province. Res. Environ. Yangtze Basin 2012, 21, 181–186. [Google Scholar]
- Li, X.; Qu, F.; Jiang, D.; Zhu, P. Integrated benefits of power generation by straw biomass—A case study on the Sheyang Straw Power Plants in Jiangsu Province, China. Front. Environ. Sci. Eng. China 2009, 3, 348–353. [Google Scholar] [CrossRef]
- China National Renewable Energy Centre. 13rd Five-Year Plan of Biomass Energy Development; China National Energy Administration: Beijing, China, 2016.
- Zhang, Q.; Zhou, D.; Fang, X. Analysis on the policies of biomass power generation in china. Renew. Sustain. Energy Rev. 2015, 32, 926–935. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhou, D.Q.; Zhou, P.; Ding, H. Cost analysis of straw-based power generation in Jiangsu province, China. Appl. Energy 2013, 102, 785–793. [Google Scholar] [CrossRef]
- Comber, A.; Dickie, J.; Jarvis, C.; Phillips, M.; Tansey, K. Locating bioenergy facilities using a modified gis-based location-allocation-algorithm: Considering the spatial distribution of resource supply. Appl. Energy 2015, 154, 309–316. [Google Scholar] [CrossRef]
- Höhn, J.; Lehtonen, E.; Rasi, S.; Rintala, J. A geographical information system (GIS) based methodology for determination of potential biomasses and sites for biogas plants in southern Finland. Appl. Energy 2014, 113, 1–10. [Google Scholar] [CrossRef]
- Lv, H.; Ding, H.; Zhou, D.Q.; Zhou, P. A site selection model for a straw-based power generation plant with CO2 emissions. Sustainability 2014, 6, 7466–7481. [Google Scholar] [CrossRef]
- Chen, C.; Huang, G.; Li, Y.; Li, M. Model of risk analysis on site selection of biomass power plant based on stochastic robust interval method. Trans. Chin. Soc. Agric. Eng. 2013, 29, 206–213. [Google Scholar]
- Chen, C.; Li, W.; Li, Y.; Zhu, Y. Biomass power plant site selection modeling and decision optimization. Trans. Chin. Soc. Agric. Eng. 2011, 27, 255–260. [Google Scholar]
- Velazquez-Marti, B.; Fernandez-Gonzalez, E. Mathematical algorithms to locate factories to transform biomass in bioenergy focused on logistic network construction. Renew. Energy 2010, 35, 2136–2142. [Google Scholar] [CrossRef]
- Wang, L.L.; Watanabe, T. A stackelberg game theoretic analysis of incentive effects under perceived risk for China’s straw-based power plant supply chain. Energies 2016, 9, 20. [Google Scholar] [CrossRef]
- Biberacher, M.; Tum, M.; Gunther, K.P.; Gadocha, S.; Zeil, P.; Jilani, R.; Mansha, M. Availability assessment of bioenergy and power plant location optimization: A case study for Pakistan. Renew. Sustain. Energy Rev. 2015, 42, 700–711. [Google Scholar] [CrossRef]
- Kumar, A.; Cameron, J.B.; Flynn, P.C. Biomass power cost and optimum plant size in western Canada. Biomass Bioenergy 2003, 24, 445–464. [Google Scholar] [CrossRef]
- Shi, X.; Elmore, A.; Li, X.; Gorence, N.J.; Jin, H.M.; Zhang, X.H.; Wang, F. Using spatial information technologies to select sites for biomass power plants: A case study in Guangdong province, China. Biomass Bioenergy 2008, 32, 35–43. [Google Scholar] [CrossRef]
- Franco, C.; Bojesen, M.; Hougaard, J.L.; Nielsen, K. A fuzzy approach to a multiple criteria and geographical information system for decision support on suitable locations for biogas plants. Appl. Energy 2015, 140, 304–315. [Google Scholar] [CrossRef]
- Panichelli, L.; Gnansounou, E. Gis-based approach for defining bioenergy facilities location: A case study in northern spain based on marginal delivery costs and resources competition between facilities. Biomass Bioenergy 2008, 32, 289–300. [Google Scholar] [CrossRef]
- Perpina, C.; Alfonso, D.; Perez-Navarro, A.; Penalvo, E.; Vargas, C.; Cardenas, R. Methodology based on geographic information systems for biomass logistics and transport optimisation. Renew. Energy 2009, 34, 555–565. [Google Scholar] [CrossRef]
- Sultana, A.; Kumar, A. Optimal siting and size of bioenergy facilities using geographic information system. Appl. Energy 2012, 94, 192–201. [Google Scholar] [CrossRef]
- Bojesen, M.; Birkin, M.; Clarke, G. Spatial competition for biogas production using insights from retail location models. Energy 2014, 68, 617–628. [Google Scholar] [CrossRef]
- Lin, T.; Wang, S.W.; Rodriguez, L.F.; Hu, H.; Liu, Y. Cybergis-enabled decision support platform for biomass supply chain optimization. Environ. Model. Softw. 2015, 70, 138–148. [Google Scholar] [CrossRef]
- Hu, H.; Lin, T.; Liu, Y.Y.; Wang, S.W.; Rodriguez, L.F. Cybergis-bioscope: A cyberinfrastructure-based spatial decision-making environment for biomass-to-biofuel supply chain optimization. Concurr. Comput. Pract. Exp. 2015, 27, 4437–4450. [Google Scholar] [CrossRef]
- Delivand, M.K.; Cammerino, A.R.B.; Garofalo, P.; Monteleone, M. Optimal locations of bioenergy facilities, biomass spatial availability, logistics costs and ghg (greenhouse gas) emissions: A case study on electricity productions in South Italy. J. Clean Prod. 2015, 99, 129–139. [Google Scholar] [CrossRef]
- Kaundinya, D.P.; Balachandra, P.; Ravindranath, N.H.; Ashok, V. A GIS (geographical information system)-based spatial data mining approach for optimal location and capacity planning of distributed biomass power generation facilities: A case study of Tumkur district, India. Energy 2013, 52, 77–88. [Google Scholar] [CrossRef]
- Velázquez-Martí, B.; Annevelink, E. GIS application to define biomass collection points as sources for linear programming of delivery networks. Trans. ASAE 2009, 52, 1069–1078. [Google Scholar] [CrossRef]
- Gracia, C.; Velázquez-Martí, B.; Estornell, J. An application of the vehicle routing problem to biomass transportation. Biosyst. Eng. 2014, 124, 40–52. [Google Scholar] [CrossRef]
- Lin, T.; Rodriguez, L.F.; Shastri, Y.N.; Hansen, A.C.; Ting, K.C. Gis-enabled biomass-ethanol supply chain optimization: Model development and miscanthus application. Biofuels Bioprod. Biorefining 2013, 7, 314–333. [Google Scholar] [CrossRef]
- Rozakis, S.; Kremmydas, D.; Pudelko, R.; Borzecka-Walker, M.; Faber, A. Straw potential for energy purposes in poland and optimal allocation to major co-firing power plants. Biomass Bioenergy 2013, 58, 275–285. [Google Scholar] [CrossRef]
- Wang, W.; Liu, Y.D.; Zhang, L. The spatial distribution of cereal bioenergy potential in china. GCB Bioenergy 2013, 5, 525–535. [Google Scholar] [CrossRef]
- Wang, F.; Shi, X. Geospatial analysis for utilizing the marginal land in regional biofuel industry: A case study in Guangdong province, China. Biomass Bioenergy 2015, 83, 302–310. [Google Scholar] [CrossRef]
- Moghadam, A.M.; Piroozfard, H.; Ma’aram, A.; Mirzapour, S.A. Solving a capacitated p-median location allocation problem using genetic algorithm: A case study. Adv. Mater. Res. 2014, 845, 569–573. [Google Scholar] [CrossRef]
- Tong, D.Q.; Murray, A.; Xiao, N.C. Heuristics in spatial analysis: A genetic algorithm for coverage maximization. Ann. Assoc. Am. Geogr. 2009, 99, 698–711. [Google Scholar] [CrossRef]
- Chaudhry, S.S.; He, S.W.; Chaudhry, P.E. Solving a class of facility location problems using genetic algorithms. Expert Syst. 2003, 20, 86–91. [Google Scholar] [CrossRef]
- Alp, O.; Erkut, E.; Drezner, Z. An efficient genetic algorithm for the p-median problem. Ann. Oper. Res. 2003, 122, 21–42. [Google Scholar] [CrossRef]
- Wightman, J.L.; Ahmed, Z.U.; Volk, T.A.; Castellano, P.J.; Peters, C.J.; DeGloria, S.D.; Duxbury, J.M.; Woodbury, P.B. Assessing sustainable bioenergy feedstock production potential by integrated geospatial analysis of land use and land quality. BioEnergy Res. 2015, 8, 1671–1680. [Google Scholar] [CrossRef]
- Vavrova, K.; Knapek, J.; Weger, J. Modeling of biomass potential from agricultural land for energy utilization using high resolution spatial data with regard to food security scenarios. Renew. Sustain. Energy Rev. 2014, 35, 436–444. [Google Scholar] [CrossRef]
- Wang, X.; Shuai, X.; Xie, G. Value-taking for residue factor as a parameter to assess the field residue of field crops. J. Chin. Agri. Univ. 2012, 17, 1–8. [Google Scholar] [CrossRef]
- Xie, G.; Wang, X.; Han, D.; Shuai, X. Harvest index and residue factor of non-cereal crops in China. J. Chin. Agri. Univ. 2011, 16, 9–17. [Google Scholar]
- Cao, J.; Pang, B.; Mo, X.P.; Xu, F.Y. A new model that using transfer stations for straw collection and transportation in the rural areas of China: A case of Jinghai, Tianjin. Renew. Energy 2016, 99, 911–918. [Google Scholar] [CrossRef]
- Jiang, D.; Zhuang, D.F.; Fu, J.Y.; Huang, Y.H.; Wen, K.G. Bioenergy potential from crop residues in China: Availability and distribution. Renew. Sustain. Energy Rev. 2012, 16, 1377–1382. [Google Scholar] [CrossRef]
- Eiselt, H.A.; Marianov, V. Gradual location set covering with service quality. Socio-Econ. Plan. Sci. 2009, 43, 121–130. [Google Scholar] [CrossRef]
- Karasakal, O.; Karasakal, E.K. A maximal covering location model in the presence of partial coverage. Comput. Oper. Res. 2004, 31, 1515–1526. [Google Scholar] [CrossRef]
- Richard, L.; Church, K.L.R. Generalized coverage models and public facility location. Pap. Reg. Sci. Assoc. 1983, 53, 117–135. [Google Scholar]
- Qi, T.; Zhang, X.; Ou, X.; Liu, Z.; Chang, S. The regional cost of biomass direct combustion power generation in China and development potential analysis. Renew. Energy Res. 2011, 29, 115–118. [Google Scholar]
- China National Renewable Energy Centre. Renewable Energy Data Sheet; China National Energy Administration: Beijing, China, 2015.
- Ma, J.; Scott, N.R.; DeGloria, S.D.; Lembo, A.J. Siting analysis of farm-based centralized anaerobic digester systems for distributed generation using GIS. Biomass Bioenergy 2005, 28, 591–600. [Google Scholar] [CrossRef]
- Castro, L.N.D.; Timmis, J.I. Artificial immune systems as a novel soft computing paradigm. Soft Comput. 2003, 7, 526–544. [Google Scholar] [CrossRef]
- Timmis, J.; Hone, A.; Stibor, T.; Clark, E. Theoretical advances in artificial immune systems. Theor. Comput. Sci. 2008, 403, 11–32. [Google Scholar] [CrossRef]
- Zhao, X.; Liu, Y.L.; Liu, D.F.; Ma, X.Y. Aitso: A tool for spatial optimization based on artificial immune systems. Comput. Intell. Neurosci. 2015, 2015, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Ma, X.Y.; Zhao, X. Land use allocation based on a multi-objective artificial immune optimization model: An application in Anlu county, China. Sustainability 2015, 7, 15632–15651. [Google Scholar] [CrossRef]
- Huang, K.N.; Liu, X.P.; Li, X.; Liang, J.Y.; He, S.J. An improved artificial immune system for seeking the pareto front of land-use allocation problem in large areas. Int. J. Geogr. Inf. Sci. 2013, 27, 922–946. [Google Scholar] [CrossRef]
- Liu, X.P.; Li, X.; Tan, Z.Z.; Chen, Y.M. Zoning farmland protection under spatial constraints by integrating remote sensing, GIS and artificial immune systems. Int. J. Geogr. Inf. Sci. 2011, 25, 1829–1848. [Google Scholar] [CrossRef]
- What Is a Geodatabase? Available online: http://desktop.arcgis.com/en/arcmap/latest/manage-data/geodatabases/what-is-a-geodatabase.htm (accessed on 10 February 2017).
- Statistical Bureau of Hubei Province. Statistical Yearbook of Hubei 2016; China Statistics Press: Beijing, China, 2016.
- Tan, L.S.; Zhang, Y.C. Optimal resource allocation with principle of equality and diminishing marginal utility in wireless networks. Wirel. Person. Commun. 2015, 84, 671–693. [Google Scholar] [CrossRef]










| Crop | Straw/Production Ratio |
|---|---|
| Wheat | 1.16 |
| Rice | 0.96 |
| Corn | 1.75 |
| Cotton | 3.44 |
| Rape | 2.04 |
| Wheat | 1.16 |
| ID | Constraints | Value |
|---|---|---|
| 1 | Distance to natural protected areas | ≥3000 m |
| 2 | Distance to airport | ≥2000 m |
| 3 | Distance to urban area | ≥3000 m |
| 4 | Distance to rural settlements | ≥1000 m |
| 5 | Distance to wetland | ≥1500 m |
| 6 | Distance to highway | ≤1000 m |
| 7 | Slope | ≤15° |
| 8 | Available straw in supply area | ≥18 tons [48] |
| Districts | Cropping Systems |
|---|---|
| E Zhou (EZ) | Rp-Rc-Rc; W-Rc; W-Ct |
| En Shi (ES) | Rc-Rc; W-Rc; W-Cn |
| Huang Gang (HG) | Rp-Rc-Rc; W-Rc; W-Ct; W-Cn |
| Huang Shi (HS) | Rp-Rc-Rc; W-Rc; W-Ct |
| Jing Men (JM) | Rp-Rc-Rc; W-Rc; W-Ct |
| Jing Zhou (JZ) | Rp-Rc-Rc; W-Rc; W-Ct |
| Qian Jiang (QJ) | Rp-Rc-Rc; W-Rc; W-Ct |
| Tian Men (TM) | Rp-Rc-Rc; W-Rc; W-Ct |
| Xian Tao (XT) | Rp-Rc-Rc; W-Rc; W-Ct |
| Shen Nong Jia (SNJ) | W-Rc; W-Cn; Rp-Cn |
| Shi Yan (SY) | W-Rc; W-Cn; Rp-Cn |
| Sui Zhou (SZ) | Rp-Rc; W-Rc; W-Ct |
| Wu Han (WH) | Rp-Rc-Rc; W-Rc; W-Ct |
| Xian Ning (XN) | Rp-Rc-Rc; W-Rc; W-Ct |
| Xiang Yang (XY) | W-Rc; W-Cn; W-Ct; Rp-Rc |
| Xiao Gan (XG) | Rp-Rc-Rc; W-Rc; W-Ct |
| Yi Chang (YC) | W-Rc; W-Cn; Rp-Cn |
| Number of SPPs | Total Benefit (Million CNY) | Total Transportation Cost (Million CNY) | Total Straw Yield (Million tons) | Marginal Revenue (Million CNY) | ||
|---|---|---|---|---|---|---|
| Without Subsidy | With Subsidy | Without Subsidy | With Subsidy | |||
| 5 | 956 | 1215. | 211 | 3.24 | - | - |
| 10 | 1700 | 2160 | 370 | 5.75 | 148.78 | 188.91 |
| 15 | 2243 | 2851 | 493 | 7.60 | 108.63 | 138.21 |
| 20 | 2783 | 3535 | 601 | 9.40 | 107.97 | 136.78 |
| 25 | 3292 | 4178 | 694 | 11.08 | 101.93 | 128.71 |
| 30 | 3608 | 4574 | 739 | 12.08 | 63.18 | 79.22 |
| 35 | 3905 | 4947 | 782 | 13.02 | 59.39 | 74.48 |
| 40 | 4115 | 5208 | 802 | 13.66 | 42.04 | 52.26 |
| 45 | 4286 | 5420 | 818 | 14.18 | 34.16 | 42.46 |
| 50 | 4428 | 5592 | 809 | 14.55 | 28.41 | 34.37 |
| 55 | 4526 | 5711 | 810 | 14.82 | 19.46 | 23.83 |
| 60 | 4589 | 5781 | 772 | 14.90 | 12.75 | 13.89 |
| 65 | 4608 | 5801 | 761 | 14.92 | 3.73 | 4.09 |
| Number of SPPs | Average Transport Distance of Straw (km) | Supply Area (km2) | Available Straw (1000 tons) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Max | Min | Avg | Total | Max | Min | Avg | Total | ||
| 35 | 24.0 | 3719 | 1521 | 2668 | 93,366 | 636 | 197 | 372 | 13,021 |
| 40 | 23.5 | 3572 | 207 | 2347 | 93,868 | 585 | 181 | 342 | 13,660 |
| 45 | 23.1 | 3326 | 463 | 2121 | 95,453 | 504 | 195 | 315 | 14,179 |
| 50 | 22.3 | 3177 | 887 | 2001 | 100,044 | 465 | 185 | 291 | 14,551 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, X.; Ma, X.; Wang, K.; Long, Y.; Zhang, D.; Xiao, Z. A Spatially Explicit Optimization Model for Agricultural Straw-Based Power Plant Site Selection: A Case Study in Hubei Province, China. Sustainability 2017, 9, 832. https://doi.org/10.3390/su9050832
Zhao X, Ma X, Wang K, Long Y, Zhang D, Xiao Z. A Spatially Explicit Optimization Model for Agricultural Straw-Based Power Plant Site Selection: A Case Study in Hubei Province, China. Sustainability. 2017; 9(5):832. https://doi.org/10.3390/su9050832
Chicago/Turabian StyleZhao, Xiang, Xiaoya Ma, Kun Wang, Yuqing Long, Dongjie Zhang, and Zhanchun Xiao. 2017. "A Spatially Explicit Optimization Model for Agricultural Straw-Based Power Plant Site Selection: A Case Study in Hubei Province, China" Sustainability 9, no. 5: 832. https://doi.org/10.3390/su9050832
APA StyleZhao, X., Ma, X., Wang, K., Long, Y., Zhang, D., & Xiao, Z. (2017). A Spatially Explicit Optimization Model for Agricultural Straw-Based Power Plant Site Selection: A Case Study in Hubei Province, China. Sustainability, 9(5), 832. https://doi.org/10.3390/su9050832