Differences in Infiltration and Evaporation of Diesel and Gasoline Droplets Spilled onto Concrete Pavement
Abstract
:1. Introduction
2. Experimental Methods
Experimental Protocol
- Concrete samples were placed into the fume hood several hours before the start of the actual spillage experiments, so that they could pre-equilibrate with the atmospheric water vapor present in the fume hood.
- We placed two concrete pieces onto the two balances. A bubble level was used to level the surface of the concrete piece such that it mimicked the usually level pavement at gasoline dispensing facilities. If needed, we put coins below the concrete pieces to achieve an upper surface that was completely horizontal.
- The balances were zeroed.
- Mass data collection was started at a frequency of 30 per minute during the first ten minutes, and 1 per minute thereafter. Also, humidity and temperature data were collected during the whole experiment at a frequency of one reading per minute.
- A small amount of fuel was then spilled over the surface of each concrete sample.
- Data were recorded for 24 h, and the experiment was terminated.
3. Data Analysis
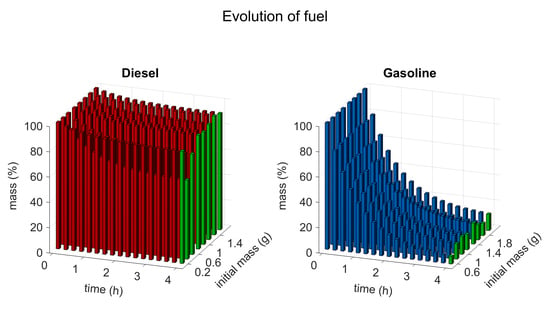
4. Results
5. Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Alternative Approach for Estimating Fuel Mass

Appendix B. Linear Regression Modeling to Assess Infiltrated Fractions as a Function of the Spill Mass

References
- Hilpert, M.; Adria-Mora, B.; Ni, J.; Rule, A.; Nachman, K. Hydrocarbon release during fuel storage and transfer at gas stations: Environmental and health effects. Curr. Environ. Health Rep. 2015, 2, 412–422. [Google Scholar] [CrossRef] [PubMed]
- Moolla, R.; Curtis, C.J.; Knight, J. Occupational exposure of diesel station workers to BTEX compounds at a bus depot. Int. J. Environ. Res. Public Health 2015, 12, 4101–4115. [Google Scholar] [CrossRef] [PubMed]
- Moolla, R.; Curtis, C.J.; Knight, J. Assessment of occupational exposure to BTEX compounds at a bus diesel-refueling bay: A case study in Johannesburg, South Africa. Sci. Total Environ. 2015, 537, 51–57. [Google Scholar] [CrossRef] [PubMed]
- Chaiklieng, S.; Pimpasaeng, C.; Thapphasaraphong, S. Benzene exposure at gasoline stations: Health risk assessment. Hum. Ecol. Risk Assess. Int. J. 2015, 21, 2213–2222. [Google Scholar] [CrossRef]
- Hakkola, M.A.; Saarinen, L.H. Customer exposure to gasoline vapors during refueling at service stations. Appl. Occup. Environ. Hyg. 2000, 15, 677–680. [Google Scholar] [PubMed]
- Lagorio, S.; Fuselli, S.; Iavarone, I.; Vanacore, N.; Carere, A. Exposure to benzene of service station employees and composition of benzene. La Medicina del Lavoro 1994, 85, 412–421. [Google Scholar] [PubMed]
- Bravo, H.; Sosa, R.; Sanchez, P.; Bueno, E.; Gonzalez, L. Concentrations of benzene and toluene in the atmosphere of the southwestern area at the Mexico City metropolitan zone. Atmos. Environ. 2002, 36, 3843–3849. [Google Scholar] [CrossRef]
- Craft, D.; Demyanovich, S.; Giraudo, M.; Johnston, J. Gasoline Service Station Industrywide Risk Assessment Guidelines; Toxics Committee of the California Air Pollution Control Officers Association (CAPCOA), Ed.; California Air Resources Board (CARB): Sacramento, CA, USA, 1997. [Google Scholar]
- Statistics Canada. Gasoline evaporative losses from retail gasoline outlets across Canada 2009. In Environment Accounts and Statistics Analytical and Technical Paper Series; Statistics Canada: Ottawa, ON, Canada, 2012. [Google Scholar]
- Levy, B.S.; Riordan, P.J.; Schreiber, R.P. Estimation of leak rates from underground storage tanks. Ground Water 1990, 28, 378–384. [Google Scholar] [CrossRef]
- Ahmed, F.E. Toxicology and human health effects following exposure to oxygenated or reformulated gasoline. Toxicol. Lett. 2001, 123, 89–113. [Google Scholar] [CrossRef]
- Morgester, J.J.; Fricker, R.L.; Jordan, G.H. Comparison of spill frequencies and amounts at vapor recovery and conventional service stations in California. J. Air Waste Manag. Assoc. 1992, 42, 284–289. [Google Scholar] [CrossRef]
- Hilpert, M.; Breysse, P.N. Infiltration and evaporation of small hydrocarbon spills at gas stations. J. Contam. Hydrol. 2014, 170, 39–52. [Google Scholar] [CrossRef] [PubMed]
- New Hampshire Department of Environmental Services. Preventing Groundwater Contamination at Gas Stations—What Municipalities and Water Suppliers Can Do; New Hampshire Department of Environmental Services: Concord, NH, USA, 2012. [Google Scholar]
- Borden, R.C.; Black, D.C.; McBlief, K.V. MTBE and aromatic hydrocarbons in North Carolina stormwater runoff. Environ. Pollut. 2002, 118, 141–152. [Google Scholar] [CrossRef]
- Drapper, D.; Hornbuckle, A. Case studies of a hydrocarbon capture technology for stormwater quality class 1 compliance against en bs858.1–2002 and subsequent field evaluation. Water 2016, 8, 48. [Google Scholar] [CrossRef]
- Stocking, A.; McDonald, S.; Woll, B.; Kavanaugh, M. Evaluation of Fate and Transport of Methyl Tertiary Butyl Ether (MTBE) in Gasoline Following a Small Spill; National Ground Water Association and American Petroleum Institute: Westerville, OH, USA; Washington, DC, USA, 1999; pp. 229–246. [Google Scholar]
- Sharma, A. Text Book of Correlations and Regression; Discovery Publishing House: New Delhi, India, 2005. [Google Scholar]
- Zou, K.H.; Tuncali, K.; Silverman, S.G. Correlation and simple linear regression. Radiology 2003, 227, 617–628. [Google Scholar] [CrossRef] [PubMed]
- Karickhoff, S.W.; Brown, D.S.; Scott, T.A. Sorption of hydrophobic pollutants on natural sediments. Water Res. 1979, 13, 241–248. [Google Scholar] [CrossRef]
- Hilpert, M.; Ben-David, A. Infiltration of liquid droplets into porous media: Effects of dynamic contact angle and contact angle hysteresis. Int. J. Multiph. Flow 2009, 35, 205–218. [Google Scholar] [CrossRef]
- Aworanti, O.A.; Agarry, S.E.; Ajani, A.O. A laboratory study of the effect of temperature on densities and viscosities of binary and ternary blends of soybean oil, soy biodiesel and petroleum diesel oil. Adv. Chem. Eng. Sci. 2012, 2, 9. [Google Scholar] [CrossRef]
- Esteban, B.; Riba, J.R.; Baquero, G.; Puig, R.; Rius, A. Characterization of the surface tension of vegetable oils to be used as fuel in diesel engines. Fuel 2012, 102, 231–238. [Google Scholar] [CrossRef]
- Methanol Institute. Methanol Safe Handling Technical Bulletin; Methanol Institute: Alexandria, VA, USA, 2011. [Google Scholar]
- Wang, F.; Wu, J.; Liu, Z. Surface tensions of mixtures of diesel oil or gasoline and dimethoxymethane, dimethyl carbonate, or ethanol. Energy Fuels 2006, 20, 2471–2474. [Google Scholar] [CrossRef]
- North Central Missouri College. Material Data Safety Sheet for #2 Diesel; North Central Missouri College: Trenton, MO, USA, 1999. [Google Scholar]
- Hess Corporation. Safety Data Sheet. Material Name: Diesel Fuel, All Types; Hess Corporation: New York, NY, USA, 2012. [Google Scholar]
- Sacile, R. Remote real-time monitoring and control of contamination in underground storage tank systems of petrol products. J. Clean. Prod. 2007, 15, 1295–1301. [Google Scholar] [CrossRef]
- The International Council On Clean Transportation (ICCT). Onboard Refueling Vapor Recovery: Evaluation of the Orvr Program in the United States; The International Council On Clean Transportation (ICCT): San Francisco, CA, USA, 2011. [Google Scholar]
- Yang, X.; Liu, H.; Cui, H.; Man, H.; Fu, M.; Hao, J.; He, K. Vehicular volatile organic compounds losses due to refueling and diurnal process in China: 2010–2050. J. Environ. Sci. 2015, 33, 88–96. [Google Scholar] [CrossRef] [PubMed]
- Speight, J.G. The Biofuels Handbook; Royal Society of Chemistry: London, UK, 2011. [Google Scholar]
- Wildenschild, D.; Culligan, K.A.; Christensen, B.S.B. Application of X-ray Microtomography to Environmental Fluid Flow Problems; SPIE: Bellingham, WA, USA, 2004; pp. 432–441. [Google Scholar]
- Cnudde, V.; Cwirzen, A.; Masschaele, B.; Jacobs, P.J.S. Porosity and microstructure characterization of building stones and concretes. Eng. Geol. 2009, 103, 76–83. [Google Scholar] [CrossRef]
- Okabe, H.; Blunt, M.J. Prediction of permeability for porous media reconstructed using multiple-point statistics. Phys. Rev. E 2004, 70, 066135. [Google Scholar] [CrossRef] [PubMed]
- Berson, A.; Choi, H.-W.; Pharoah, J.G. Determination of the effective gas diffusivity of a porous composite medium from the three-dimensional reconstruction of its microstructure. Phys. Rev. E 2011, 83, 026310. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M.; He, Y.; Ye, G.; Lange, D.A.; van Breugel, K. Computational investigation on mass diffusivity in portland cement paste based on x-ray computed microtomography (μct) image. Constr. Build. Mater. 2012, 27, 472–481. [Google Scholar] [CrossRef]
- Zhang, M.; Xu, K.; He, Y.; Jivkov, A.P. Pore-scale modelling of 3d moisture distribution and critical saturation in cementitious materials. Constr. Build. Mater. 2014, 64, 222–230. [Google Scholar] [CrossRef]
- Zhang, P.; Wittmann, F.H.; Zhao, T.J.; Lehmann, E.H.; Tian, L.; Vontobel, P. Observation and quantification of water penetration into strain hardening cement-based composites (SHCC) with multiple cracks by means of neutron radiography. Nucl. Instrum. Methods Phys. Res. Sec. A Accel. Spectrom. Detect. Assoc. Equip. 2010, 620, 414–420. [Google Scholar] [CrossRef]
- Murison, J.; Moosavi, R.; Schulz, M.; Schillinger, B.; Schröter, M. Neutron tomography as a tool to study immiscible fluids in porous media without chemical dopants. Energy Fuels 2015, 29, 6271–6276. [Google Scholar] [CrossRef]
- Wildenschild, D.; Sheppard, A.P. X-ray imaging and analysis techniques for quantifying pore-scale structure and processes in subsurface porous medium systems. Adv. Water Resour. 2013, 51, 217–246. [Google Scholar] [CrossRef]
- Lau, E.V.; Gan, S.; Ng, H.K. Extraction techniques for polycyclic aromatic hydrocarbons in soils. Int. J. Anal. Chem. 2010, 2010, 9. [Google Scholar] [CrossRef] [PubMed]
- Zimmerman, A.J.; Weindorf, D.C. Heavy metal and trace metal analysis in soil by sequential extraction: A review of procedures. Int. J. Anal. Chem. 2010, 2010. [Google Scholar] [CrossRef] [PubMed]
- United States Environmental Protection Agency (EPA). Preventing Leaks and Spills at Service Stations. A Guide for Facilities; United States Environmental Protection Agency (EPA): Washington, DC, USA, 2003.
- Alachua County Environmental Protection Dep artment. Pollution Prevention. Best Management Practices for Controlling Runoff from Gas Stations; Alachua County Environmental Protection Department: Gainesville, FL, USA, 2003. [Google Scholar]
- Connecticut Department of Energy and Environmental Protection. Best Management Practices for Fueling Stations; Connecticut Department of Energy and Environmental Protection: Hartford, CT, USA, 2015.
- Lucke, T.; Nichols, P.W.B. The pollution removal and stormwater reduction performance of street-side bioretention basins after ten years in operation. Sci. Total Environ. 2015, 536, 784–792. [Google Scholar] [CrossRef] [PubMed]
- Nichols, P.; Lucke, T. Evaluation of the long-term pollution removal performance of established bioretention cells. Int. J. GEOMATE 2016, 11, 2363–2369. [Google Scholar] [CrossRef]
- Hong, E.; Seagren, E.A.; Davis, A.P. Sustainable oil and grease removal from synthetic stormwater runoff using bench-scale bioretention studies. Water Environ. Res. 2006, 78, 141–155. [Google Scholar] [CrossRef] [PubMed]
- Dietz, M.E. Low impact development practices: A review of current research and recommendations for future directions. Water Air Soil Pollut. 2007, 186, 351–363. [Google Scholar] [CrossRef]








© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adrià Mora, B.; Hilpert, M. Differences in Infiltration and Evaporation of Diesel and Gasoline Droplets Spilled onto Concrete Pavement. Sustainability 2017, 9, 1271. https://doi.org/10.3390/su9071271
Adrià Mora B, Hilpert M. Differences in Infiltration and Evaporation of Diesel and Gasoline Droplets Spilled onto Concrete Pavement. Sustainability. 2017; 9(7):1271. https://doi.org/10.3390/su9071271
Chicago/Turabian StyleAdrià Mora, Bernat, and Markus Hilpert. 2017. "Differences in Infiltration and Evaporation of Diesel and Gasoline Droplets Spilled onto Concrete Pavement" Sustainability 9, no. 7: 1271. https://doi.org/10.3390/su9071271
APA StyleAdrià Mora, B., & Hilpert, M. (2017). Differences in Infiltration and Evaporation of Diesel and Gasoline Droplets Spilled onto Concrete Pavement. Sustainability, 9(7), 1271. https://doi.org/10.3390/su9071271