A Consistent Fuzzy Preference Relations Based ANP Model for R&D Project Selection

Abstract

In today’s rapidly changing economy, technology companies have to make decisions on research and development (R&D) projects investment on a routine bases with such decisions having a direct impact on that company’s profitability, sustainability and future growth. Companies seeking profitable opportunities for investment and project selection must consider many factors such as resource limitations and differences in assessment, with consideration of both qualitative and quantitative criteria. Often, differences in perception by the various stakeholders hinder the attainment of a consensus of opinion and coordination efforts. Thus, in this study, a hybrid model is developed for the consideration of the complex criteria taking into account the different opinions of the various stakeholders who often come from different departments within the company and have different opinions about which direction to take. The decision-making trial and evaluation laboratory (DEMATEL) approach is used to convert the cause and effect relations representing the criteria into a visual network structure. A consistent fuzzy preference relations based analytic network process (CFPR-ANP) method is developed to calculate the preference-weights of the criteria based on the derived network structure. The CFPR-ANP is an improvement over the original analytic network process (ANP) method in that it reduces the problem of inconsistency as well as the number of pairwise comparisons. The combined complex proportional assessment (COPRAS-G) method is applied with fuzzy grey relations to resolve conflicts arising from differences in information and opinions provided by the different stakeholders about the selection of the most suitable R&D projects. This novel combination approach is then used to assist an international brand-name company to prioritize projects and make project decisions that will maximize returns and ensure sustainability for the company.

1. Introduction

Both the current finances and future development of a company are impacted by research and development (R&D). For example, a high-tech company’s ability to compete can be strengthened by its ability to develop novel products giving it an edge over their competitors and opening up new markets. Consequently, R&D has come to be perceived as vital for preserving company sustainability, a major business concern and a focus for investment. It is indeed one of the key factors enhancing competitiveness. Offering a technically superior product can be a significant advantage in the marketplace, especially for high tech companies, making investment in R&D for the development of technological products very important [1]. However, it is also known that product development is dependent on the ability of a team to work together and that good teamwork is needed to smooth the product development process.

In addition, even within a company, a variety of different sources of financing may be involved all of which make R&D project selection an intricate decision-making process requiring the consideration of multiple criteria and the opinions, sometimes conflicting of different stakeholders and departments [2]. Expert opinion plays a significant role in the process of R&D project selection because the criteria for assessment of the project are determined based on their opinions [3]. Over the past years, many decision models (including economic models, mathematical programming and artificial intelligence optimization methods, as well as integrated models) have been developed to help companies make appropriate R&D project selection decisions. Nowadays, many of these methods and hybrid decision models are not widely used, having been shown to have limited effect on decision-making and R&D project selection in real world [4]. Over the past two decades, several easy to use multiple criteria decision making (MCDM) models have been proposed which have been applied by industry [5]. The MCDM models for R&D project selection include the analytic hierarchy process (AHP) [6], fuzzy analytic hierarchy process (FAHP) [7], analytic network process (ANP) [8,9], integrated the balanced scorecard (BSC) approach, data envelopment analysis (DEA) method, extended DEA models [10], technique for order preference by similarity to ideal solution (TOPSIS) [11], and hybrid models combining AHP and VlseKriterijumska Optimizacija I Kompromisno Resenje (VIKOR) [12]. Although previous MCDM studies combine to make a significant contribution, they still face three major problems: how to construct a complex evaluation system; how to integrate the various opinions from different departments; and how to reduce the decision-makers’ burden while answering a survey or questionnaire to produce consistent results.

In this work, we propose a hybrid MCDM model, integrating DEMATEL, consistent fuzzy preference relations based ANP (CFPR-ANP) and COPRAS-G methods. First, the complex evaluation system is constructed using the DEMATEL method based on which a super-matrix is formed. The CFPR-ANP method, which simplifies the super-matrix calculation, is applied to generate preference weights of criteria and finally we draw upon the CFPR-ANP method rather than the traditional ANP method, which involves time-consuming pairwise comparisons making consistent results difficult to obtain. The proposed CFPR-ANP method reduces the number of pairwise comparisons needed to obtain a consistent result. As the R&D project selection process continues, the opinions of multiple decision-makers with different points of view need to be blended together. A method is needed to aggregate the various opinions and the derived criterion weights. COPRAS-G expresses the performance values as intervals to allow managers to objectively select alternatives. The proposed integrated model applies fuzzy concepts making is more suitable for R&D evaluating problems.

The new integrated model offers a more effective way to solve the real-world issues involved in evaluating problems related to R&D projects. The contribution of this study is that it offers a systematic method that incorporates a complex evaluating system and uncertain information from experts of different departments or stakeholders, which can also help companies, not only evaluating the various projects but also improving the final decision performance. This method also reduces the time-consuming pairwise comparisons, which had to make in the past, while giving decision-makers more consistent outcomes. This study employs data from an international brand-name company to prioritize R&D projects and make the best project decisions, those which will maximize returns to the company and its shareholders. The rest of this paper is organized as follows: a discussion of the related literature appears in Section 2. The proposed integrated hybrid model is illustrated in Section 3. Section 4 describes our problem and the course for calculations data analysis. Section 5 includes a discussion and some conclusions and remarks are provided in Section 6.

2. The Related Literature

Decision-making for project selection issues involves fuzzy criteria and uncertainties in different situations, essentially making this an MCDM problem, and efforts to find systematic solution methods have led to the development of various decision support tools. In the past several years, numerous efforts have been made to help companies become better at making decisions in terms of R&D project selection [1,2,5]. Past studies have focused on building integrated decision models and creating decision-making methods. Decision models discussed in the literature can be divided into four types: (1) mathematical programming methods; (2) economic models; (3) artificial intelligence optimization methods; and (4) MCDM models.

2.1. Mathematical Programming Methods

Many mathematical programming methods have been adapted to create decision models for R&D project selection, including integer programming [13], linear programming [14], nonlinear programming [15], goal programming [16] and dynamic programming [17] techniques. Tavana et al. [13] proposed a model consisting of three sections that is DEA, TOPSIS, and linear integer programming for the selection of an optimal project portfolio. In a fuzzy environment, Bolat et al. [14] developed a systematic and comprehensive project selection model utilizing fuzzy multi-objective linear programming that could deal with imprecise data and the uncertain judgments of decision-makers. These studies have yielded mathematical tools such as mixed-integer or nonlinear programs that are not easy to solve and, being too complex to use, have not been applied in practice.

2.2. Economic Methods

Generally, the key factors considered in economic investment models are cost-benefit analysis, return on investment, option pricing, internal rate of return, net present value and payback period. Rzasa et al. [18] proposed a risk based methodology for improving R&D project selection and portfolio planning. Chiu and Chan [19] used the prospective NPV to assess R&D project conditions and select the optimal project. Mader [20] built a method that estimated the NPV, commercialization cost, development cost, technical success in terms of feasibility, and the probability of commercial success for the selection of a six-sigma project. Hoeck [21] applied the traditional approach of consideration of the target ROI to transformation of a revenue management technique popular with the airline industry for application to project selection and scheduling problems. Arasteh et al. [22] applied the gray system and fuzzy set theories with the real options theory for project portfolio management. Their model addressed the problem of project portfolio selection and presented some approaches for evaluating investment portfolios with an evaluation tool.

2.3. Artificial Intelligence Optimization Methods

Artificial intelligence (AI) can be defined as a computer system copying human knowledge and behavior, which has the ability to learn, judge, and solve problems, with memory-knowledge, and an understanding of natural language. In the soft computing field, it is suggested that AI would yield better predictions than traditional methods. Costantino and Nonino [23] developed an artificial neural network (ANN) for extracting the experience of project managers from a set of past successes and failures to classify the grade of project risk. Mousavi et al. [24] proposed an effective AI model applying fuzzy logic and developing new neural networks to improve the decisions for construction project selection. Huang and Zhao [25] developed a genetic algorithm to solve a scheduling and R&D project selection problem and model to measure different interactions and project flexibility. Vahdani et al. [26] proposed a new hybrid model that is comprised of a radial basis function neural network and backpropagation neural network, for the construction industry. Thieme et al. [27] used ANP results to design and train an ANN to calculate enterprise resource planning (ERP) software priorities. Although the AI methods do provide a better prediction rate for some problems, they still have some disadvantages, such as a shortage of knowledge for decision-making, inability to respond as a human expert would in special situations, and domain experts who cannot explain their reasoning and logic.

2.4. MADA Methods

MADA (Multi-Attribute Decision Analysis) methods have also been applied in many real-world problems because they are easy to use and are able to handle both qualitative and quantitative types of data. Many MADA models have been developed in the past decades, including AHP, ANP, TOPSIS, VIKOR, Step-wise Weight Assessment Ratio Analysis (SWARA), gray relations, Complex Proportional Assessment (COPRAS), COPRAS-G, etc. Dodangeh and Mojahed [11] proposed an application of the TOPSIS method for telecommunication project selection. They considered four criteria, qualitative, quantitative, negative and positive, for ranking among the best five projects. Jung and Seo [9] used an ANP approach to combine elements of programs with mixed objectives for the evaluation of R&D projects. Wang et al. [28] developed a dynamic Multi-Attribute Utility Theory (MAUT) decision model but this method ignores risk and is not sensitive to the ranking results of R&D project selection. Salehi [12] proposed a hybrid fuzzy MADA integrating AHP and VIKOR aimed at solving the project selection problem. Öztaysi [29] used AHP and interval type-2 fuzzy sets in a group to solve the problem of ERP project selection. Karaveg et al. [30] proposed a mixed-method combining structural equation modeling and TOPSIS for evaluation of R&D commercialization capacity. Yousefi and Hadi-Vencheh [31] combined the three techniques of AHP, TOPSIS and DEA for the selection of the optimal six-sigma projects. Overall, past studies have shown that the MADA models are flexible enough to enable the combination of quantitative and qualitative characteristics, for consideration of the interrelationship among criteria and weighting priorities, with the best decision being arrived at after considering the weight of each of the involved criterion. Therefore, this study develops a new hybrid MADA model for R&D project selection.

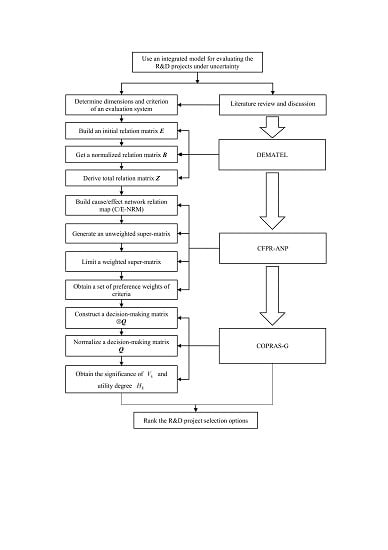
3. Proposed Integrated Hybrid Model

First, we introduce the DEMATEL analysis technique, which is used to build the interdependent structure of the influential network relation map (INRM). Then, based on this structure, the CFPR method is adopted to generate the local weights within the super-matrix of the traditional ANP approach, and to derive weights of the criteria. Finally, we apply the COPRAS-G method for evaluating the R&D projects. The proposed model is illustrated in Figure 1.

3.1. The DEMATEL Approach

Inside an evaluation system, all dimensions and criteria have some degree of interdependent relationship [32]. The DEMATEL is a technique for analyzing this complexity. Hence, this method can help users to acknowledge the interdependent relations among elements/criteria based on restricting visible systemic and developmental trends. In addition, the outcome of this approach is a visual INRM that represents the expert’s domain-knowledge about actions in the real world [33]. This diagram can help managers to understand the influential directions among the criteria of a system or sub-system. According to Fontela and Gabus [34], the calculation procedures include four steps [33]:

Step 1: Build an Initial Relation Matrix

Assume that there are n elements or criteria in the evaluation system. Then, domain-experts specify the degree of direct influence of the criterion $i$ on each criterion $j$, using an integer measurement scale. Finally, the mean values of each of the elements are indicated in the initial relation matrix $\mathit{E}={\left[e_{ij}\right]}_{n\times n}$ representing the actual experience of all domain-experts (i.e., all respondents in this study).

Step 2: Get a normalized relation matrix.

A normalized relation matrix $\mathit{B}={\left[b_{ij}\right]}_{n\times n}$ is calculated by transforming the initial relation matrix E through Equations (1) and (2). The diagonal elements equal zero in normalized relation matrix $\mathit{B}$.

$$\mathit{B}=\beta \cdot \mathit{E}, \beta >0,$$

(1)

where:

$$\beta =\min [\frac{1}{\underset{1\le i\le n}{\max }{\displaystyle \sum _{j=1}^n\left|e_{ij}\right|}},{\frac{1}{\underset{1\le j\le n}{\max }{\displaystyle \sum _{i=1}^n\left|e_{ij}\right|}}]}_{n\times n}.$$

(2)

Step 3: Derive a full relation matrix.

Let z_ij represent the element of full (or total) relation matrix $\mathit{Z}$. The matrix can be calculated using Equations (3) and (4):

$$\underset{\delta \to \infty }{\lim }{\mathit{B}}^{\delta }={\left[0\right]}_{n\times n}.$$

(3)

The full relation matrix $\mathit{Z}$ can be calculated by Equation (4) and $\mathit{I}$ is the identity matrix

$$Z=\mathit{B}+B^2+L+B^{\mathit{\delta }}=B{\left(I-B\right)}^{-\mathbf{1}}$$

(4)

when $\delta \to \infty$.

Step 4: Draw the INRM

Based on the full relation matrix $\mathit{Z}$, each component z_ij of matrix $\mathit{Z}$ provides a degree of influence about how component i affects component j. The direction of influence can be decided from the total matrix $\mathit{Z}$, if the degree of influence from i to j is larger than the degree of influence from j to i. An arrowhead is used to indicate the direction of influence from i to j. The rows and columns are summed separately to define vectors $\mathit{s}$ and $\mathit{o}$ within the full relation matrix $\mathit{Z}$ by

$$\mathit{Z}={\left[z_{ij}\right]}_{n\times n}, i,j=1,2,\cdots ,n;$$

(5)

$$\mathit{s}={\left[s_i\right]}_{n\times 1}={\left({\displaystyle \sum _{j=1}^n{z}_{ij}}\right)}_{n\times 1}=\left(s_1,\dots ,s_i,\dots ,s_n\right);$$

(6)

$$\mathit{o}={\left(o_i\right)}_{n\times 1}={\left[o_j\right]}_{1\times n}^{\text{'}}={\left({\displaystyle \sum _{i=1}^n{z}_{ij}}\right)}_{1\times n}^{\text{'}}=\left(o_1,\dots ,o_i,\dots ,o_n\right),$$

(7)

where s_i denotes the sum of the ith row of the full or total relation matrix $\mathit{Z}$ that represents the full effects of criterion i on the other elements. Likewise, o_j is the sum of the jth column in matrix $\mathit{Z}$ which represents the full effects obtained by criterion j from the other criteria. In addition, the method proposed two critical indexes for understanding the influential network relation structure within the evaluation system. The first number (s_i + o_i) is an index of the influence degree passed and obtained by criterion i. The second number (s_i − o_i) is an index of the influenced degree of the total influence.

3.2. The CFPR-Based ANP Method

After obtaining the network structure obtained through the DEMATEL analysis, the super-matrix of the evaluation system can be constructed. Instead of using the original ANP method, the CFPR method is applied to build the super-matrix to reduce the time-consuming pairwise comparisons between criteria and produce more consistent results. This novel method is called the CFPR-based ANP method. In the CFPR, the decision maker’s preference for a set of alternatives $P$ is indicated by a positive preference relation matrix $R\subset P\times P$ with ${\rho }_R:P\times P\to \left[0,1\right]$, where ${\rho }_R\left(x_{i,}{x}_j\right)=r_{ij}$ indicates the ratio of the preference intensity of alternative $p_i$ to that of $p_j$. Here, $r_{ij}=0.5$ means no difference between $p_i$ and $p_j\left(p_i~p_j\right)$; $f_{ij}>0.5$ implies that means that $p_i$ is preferred to $p_j\left(p_i>p_j\right)$ $f_j=1$ and indicates that $p_i$ is absolutely preferred to $p_i$; and $f_{ij}=0$ indicates that $p_i$ is absolutely preferred to $p_i$. The $F$ is an additive reciprocal given by $f_{ij}+f_{ji}=1,\forall i,j\in \left\{1,2,\cdots ,n\right\}$.

Herrera-Viedma et al. [35] proved that for a reciprocal additive fuzzy preference relation $F=\left(f_{ij}\right)$:

$$\begin{array}{cc}{f}_{ij}+f_{jk}+f_{ki}=\frac{3}{2}& \forall i<j<k\end{array};$$

(8)

$$\begin{array}{c}{f}_{i(i+1)}+f_{(i+1)(i+2)}+\cdots +f_{(j-i)j}=(j-i+1)/2\end{array}$$

(9)

for each i < j.

Based on Equation (9), we can obtain Equation (10).

$$\begin{array}{cc}{f}_{ji}=\frac{j-i+1}{2}-f_{i(i+1)}-f_{(i+1)(i+2)}-\cdots -f_{(j-i)j}& \forall i<j\end{array}.$$

(10)

In addition, from the additive reciprocal relation Equation (11), we can derive the other elements of the pairwise comparisons.

$$f_{ij}+f_{ji}=1,\forall i,j\in \left\{1,2,\cdots ,n\right\}.$$

(11)

The CFPR analysis steps can be summarized as following:

Step 1: Calculate preference values $X$

$$X=\left\{f_{ij,}i<j\wedge f_{ij}\notin \left\{f_{12,}{f}_{23,}\cdots f_{n-1n}\right\}\right\};$$

(12)

Step 2: Find $F$

$$F=\left\{f_{12,}{f}_{23,}\cdots f_{n-1n}\right\}\cup X\cup \left\{1-f_{12,}1-f_{23,}\cdots ,1-f_{n-1n}\right\}\cup \neg X;$$

(13)

Step 3: Calculate $F^{\prime }$

$$F^{\text{'}}=\phi \left(F\right), \mathrm{such} \mathrm{that} \phi :\left[\begin{array}{cc}-d,& 1+d\end{array}\right]\to \left[\begin{array}{cc}0,& 1\end{array}\right];$$

$$\phi \left(p\right)=\frac{p+d}{1+2d}.$$

(14)

For n attributes, $P=\left\{\begin{array}{cc}{p}_1,p_2,\cdots ,p_n& n\ge 2\end{array}\right\}$, the comparisons between any two attributes can be derived by comparing $n-1$ times and constructing a consistent reciprocal fuzzy preference relation $F^{\text{'}}$. Using the fuzzy preference relation data, we can derive the priorities of each vector in the unweighted super-matrix. The weighted super-matrix can be multiplied itself to the limiting power until each row has converge to a constant value, which each row number indicates the influential weight of criterion.

$$\underset{\tau \to \infty }{\lim }{(W)}^{\tau }.$$

(15)

3.3. Modified COPRAS-G Method

The criteria weights obtained from the limiting super-matrix, combined with the performance values, form the basis for the modified COPRAS-G method proposed by Zavadskas et al. [36] to compute the degree of utility and order of priority of the R&D projects. This modified method works by presenting a stepwise ranking and evaluation process of the projects in terms of their significance and utility degree as follows:

Step 1: Construct the decision-making matrix $\otimes \mathit{Q}$.

$$\otimes \mathit{Q}=\left[\begin{array}{ccccc}\left[l_{11};u_{11}\right]& \cdots & \left[l_{1j};u_{1j}\right]& \cdots & \left[l_{1n};u_{1n}\right]\\ ⋮& & ⋮& & ⋮\\ \left[l_{k1};u_{k1}\right]& \cdots & \left[l_{kj};u_{kj}\right]& \cdots & \left[l_{kn};u_{kn}\right]\\ ⋮& & ⋮& & ⋮\\ \left[l_{m1};u_{m1}\right]& \cdots & \left[l_{mj};u_{mj}\right]& \cdots & \left[l_{mn};u_{mn}\right]\end{array}\right]; k=1,2,\mathrm{\dots },m;j=1,2,\mathrm{\dots },n.$$

(16)

where $l_{kj}$ is the lower limit; and $u_{kj}$ is the upper limit for the $j^{th}$ criteria, respective of the $k^{th}$ alternative.

Step 2: Normalize the decision-making matrix Q

$$\overline{l_{kj}}=\frac{l_{kj}}{u_j^{aspire}-u_j^{worst}};$$

$$\overline{u_{kj}}=\frac{u_{kj}}{u_j^{aspire}-u_j^{worst}};k=1,2,\mathrm{\dots },m;j=1,2,\mathrm{\dots },n.$$

(17)

During the process of normalizing the performance matrix, ratings are frequently made using natural language. In this study, we set the aspiration level to 10 (absolutely good) and the worst value to 0 (absolutely poor).

Step 3: Compute the interval values of the grey relations

The grey relationship coefficients are calculated as follows:

$$\gamma ({\overline{u}}_j^{aspire},\overline{l_{kj}})=\frac{\underset{k}{\min } \underset{j}{\min }|{\overline{u}}_j^{aspire}-\overline{l_{kj}}|+\varsigma \underset{k}{\max } \underset{j}{\max }|{\overline{u}}_j^{aspire}-\overline{l_{kj}}|}{|{\overline{u}}_j^{aspire}-\overline{l_{kj}}|+\varsigma \underset{k}{\max }\underset{j}{\max }|{\overline{u}}_j^{aspire}-\overline{l_{kj}}|}$$

(18)

$$\gamma ({\overline{u}}_j^{aspire},\overline{u_{kj}})=\frac{\underset{k}{\min } \underset{j}{\min }|{\overline{u}}_j^{aspire}-\overline{u_{kj}}|+\varsigma \underset{k}{\max } \underset{j}{\max }|{\overline{u}}_j^{aspire}-\overline{u_{kj}}|}{|{\overline{u}}_j^{*}-\overline{u_{kj}}|+\varsigma \underset{k}{\max }\underset{j}{\max }|{\overline{u}}_j^{aspire}-\overline{u_{kj}}|}$$

(19)

The distinguishing coefficient ($\varsigma$) can be adjusted by the decision maker exercising judgment, and different distinguishing coefficients usually produce different results of grey relational analysis. In this paper, the distinguishing coefficient was set as 0.5.

The interval grade of grey relation $\gamma (({\overline{u}}_{}^{asspire},\overline{l_k});({\overline{u}}_{}^{aspire},\overline{u_k}))$ is

$$\gamma ((u_{}^{aspire},\overline{l_k});(u_{}^{aspire},\overline{u_k}))={\displaystyle \sum _{j=1}^n{w}_j}(\gamma ({\overline{u}}_j^{aspire},\overline{l_{kj}});\gamma ({\overline{u}}_j^{aspire},\overline{u_{kj}})).$$

(20)

where $\gamma ({\overline{u}}_{}^{aspire},\overline{l_k})={\displaystyle \sum _{j=1}^n{w}_j}\gamma ({\overline{u}}_j^{aspire},\overline{l_{kj}})$ and $\gamma ({\overline{u}}_{}^{aspire},\overline{u_k})={\displaystyle \sum _{j=1}^n{w}_j}\gamma ({\overline{u}}_j^{aspire},\overline{u_{kj}})$, and the aspiration levels of ${\overline{u}}_{}^{aspire}$ and ${\overline{u}}_j^{aspire}$ are set by decision-makers.

Step 4: Obtain the significance of the $V_k$ value and utility degree $H_k$.

The relative significance $V_k$ can be obtained by Equation (21).

$$V_k=\frac{1}{2}(\gamma ({\overline{u}}^{aspire},{\overline{l}}_k)+\gamma ({\overline{u}}^{aspire},{\overline{u}}_k)).$$

(21)

Finally, the utility degree $H_k$ can be obtained by Equation (22).

$$H_k^{}=\frac{V_k^{}}{U^{aspire}}\times 100\%.$$

(22)

where $U^{aspire}$ is aspiration level for the alternative.

4. Empirical Example: Brand-Name Company

This case uses data for a well-known international enterprise specializing in the manufacturing and distribution of brand-name computing hardware products. It is also a leading provider of motherboards (ranked second in the world). Other products they produce can be divided into four categories: computers (note-book, tablet and desktop computers), hardware of computer peripherals (mother boards, mice, keyboards, power supplies, cooling components, and computer chassis), high-end graphics cards, and Internet server equipment (computing servers and storage servers, racks, and network cards). The company has been listed on the Taiwan Stock Exchange (TSE) since 24 September 1998. With a capital worth of approximately US$ 197.61 million and gross revenue of about US$ 1595.39 million in 2016, they employ nearly 8000 employees worldwide, and work in cooperation with global leaders in technology including Intel, AMD, Microsoft and so on to develop key technology. Their global operations include support centers in 34 areas or countries in Europe, Asia, Africa, Oceania, the Middle East, South America, and North America. Currently, the case company has too many ongoing R&D projects for the development of various products, which has caused investment inefficiency and a gradual loss in market competitiveness. For the sake of sustaining growth and ensuring future development, the case company has decided to downsize the number and scale of R&D projects, selecting only the most competitive to invest in, in order to maximize profit and preserve sustainability. They urgently need a useful tool to help them make the most appropriate R&D project selection decisions.

4.1. Criteria and Dimensions for R&D Project Selection

In practice, it is not possible to use all criteria for all cases and there is considerable variation from market to market and product to product, as well as the operational environment of the company. From a literature review, we first prepared a list four dimensions and 25 criteria that are related to R&D project selection. Then, 18 managers from different departments in the case company were invited to rank the importance of the criteria. The departments included marketing, manufacturing, R&D, finance, and logistics. The managers ranked the degree of importance of each criterion on the five-point scale ranging from very important to no effect on R&D projects. After reviewing the results of the survey and after several rounds of discussion with managers, we selected 13 criteria as the basis for an evaluation system, comprised of four dimensions, each with three or four criteria. The importance of the dimensions varies with the phase of the project life. The final selected dimensions and their corresponding criteria are as follows:

(1)

Research and development: A successful project relies on the probability of technical success, availability of resources, and applicability to other products and processes.

(2)

Manufacturing: The project needs to fit the firm’s manufacturing capability, facility and equipment requirements, and raw materials and components available.

(3)

Marketing and distribution: The potential markets and possible channels for distribution must be viable for company sustainability. Considerations include potential size of the market, competitors’ efforts in similar areas, probability of market success of the product, and product life.

(4)

Financial considerations: It is impossible for a project to be launched without considering financing. The capital investment required, rate of return on investment, and unit price of the product are the criteria considered within the financial dimension.

A summary of the dimensions, criteria and reference sources used in the project selection problem appears in

Table 1. R&D project selection criteria and referenced literature.

Dimension	Literature	Criteria	Literature
R&D (C1)	[9,11,37]	Probability of technical success (C11)	[9,11,37]
		Availability of R&D resources (C12)	[11,37]
		Applicability to other products and processes (C13)	[11]
Manufacturing (C2)	[9,37]	Fits manufacturing capability (C21)	[37]
		Facility and equipment requirements (C22)	[37]
		raw material/ component (C23)	[9]
Marketing (C3)	[1,9,11,37]	Potential size of market (C31)	[9,11,37]
		Competitor efforts in similar areas (C32)	[9,11]
		Probability of market success of product (C33)	[11,37]
		Product life (C34)	[9]
Finance (C4)	[11,37]	Capital investment required (C41)	[37]
		Rate of return on investment (C42)	[11,37]
		Unit price of product (C43)	[37]

.

4.2. Measuring Relationships among Dimensions

Given the interdependent relationships in the evaluation system, the DEMATEL method is utilized to construct the network relationships. The cause-and-effect for each dimension is derived from the INRM. In the initial DEMATEL survey, managers were asked to define the degree of influence of the different dimensions.

Table 2. Initial influence matrix E.

	R&D	Manufacturing	Marketing	Finance
R&D (C1)	0	0.37	0.35	0.28
Manufacturing (C2)	0.30	0	0.21	0.24
Marketing (C3)	0.31	0.20	0	0.26
Finance (C4)	0.27	0.25	0.28	0

shows the average initial relation 4 × 4 matrix E obtained through pairwise comparisons as well as the influences and direction of influence between dimensions. From the initial influence matrix E (Table 2), the normalized relation B can be calculated using Equations (1) and (2). Then, using Equations (6) and (7), we can determine the full or total influence Z, as shown in Table 4.

The setting of the threshold value is usually influenced by the complexity of the problem and the disagreement of the expert opinions. The over-high threshold value does not properly reduce the meaning of the expert opinions, over-simplifies the problem, and the very low threshold leads to disagreement and lack of focus. Therefore, this study used a simple method to set the threshold value. After consulting and discussing with the experts in this field, a threshold value of 1.16 was decided for the total influence matrix (

Table 3. Full relation matrix Z.

	R&D	Manufacturing	Marketing	Finance
R&D (C1)	1.26	1.48	1.49	1.38
Manufacturing (C2)	1.25	0.98	1.17	1.14
Marketing (C3)	1.27	1.16	1.01	1.16
Finance (C4)	1.27	1.21	1.25	0.97

). A value of less than 1.16 would make the relationship for the entire system too complex to be evident. Based on this threshold value, the network structure of the evaluating system is plotted, as shown in Figure 2. It can be seen that research and development is located at the center of the system and has a strong interaction with other dimensions. Finance is at the top, influencing both manufacturing and marketing. Manufacturing is affected by finance and finance will influence marketing. Marketing is the affected dimension and is influenced by the other dimensions. The INRM shown in Figure 3, plotted based on the results in Table 3 and

Table 4. Sum of affects for the various dimensions.

Dimensions	${\mathit{s}}_{\mathit{i}}+{\mathit{o}}_{\mathit{i}}$	${\mathit{s}}_{\mathit{i}}-{\mathit{o}}_{\mathit{i}}$
R&D (C1)	10.64	0.56
Manufacturing (C2)	9.36	−0.29
Marketing and distribution (C3)	9.52	−0.32
Finance (C4)	9.34	0.04

, indicates the direction of influence in combination with the cause-and-effect relationship. Based on the derived INRM, managers can see which elements are the causes of an influence and thus understand the best direction for improvement.

4.3. Weighting of Criteria for R&D Project Selection

After determining the network structure relations between the factors for R&D project selection, the CFPR-ANP method is applied to determine the criterion weights. In Figure 2, we can decide the structure of the super-matrix. Then, the importance of each criterion is compared to construct the local weights in the super-matrix. For example, domain experts were requested to reply a series of questions, such as “For the probability of technical success, how much more important is manufacturing capability (C₂₁) over facility and equipment requirements (C₂₂).” They were asked to score pairwise comparisons on the nine-point scale, ranging from 1 indicating equal importance to 9 indicating extreme importance. ANP is the generalized form of AHP to solve the interdependent problems between criteria. Because the ANP discusses complex interrelationships between clusters/attributes, it needs n(n − 1)/2 pairwise comparisons for n criteria in a cluster. However, our proposed CFPR-ANP model only requires n − 1 comparisons, thereby avoiding spending too much time on the pairwise comparisons process. Calculating the eigenvectors of each matrix, we can derive the local weights of criteria to form the unweighted super-matrix. In addition, the original ANP needs to check the consistent index, and the CFPR-ANP resolves the shortcoming. The inconsistency is resolved based on the additive transitivity property of the consistent fuzzy preference relation using Equations (8) to (14) to construct the pairwise comparison matrices. In this hybrid CFPR-ANP method, consistency checks are not required and all pairwise comparisons are consistent [38]. Therefore, using the proposed CFPR-ANP can generate consistent results with less time and greatly improves decision efficiency. The unweighted super-matrix is generated as in

Table 5. The unweighted super-matrix.

	${\mathit{C}}_{11}$	${\mathit{C}}_{12}$	${\mathit{C}}_{13}$	${\mathit{C}}_{21}$	${\mathit{C}}_{22}$	${\mathit{C}}_{23}$	${\mathit{C}}_{31}$	${\mathit{C}}_{32}$	${\mathit{C}}_{33}$	${\mathit{C}}_{34}$	${\mathit{C}}_{41}$	${\mathit{C}}_{42}$	${\mathit{C}}_{43}$
$C_{11}$	0	0	0	0.39	0.37	0.31	0.39	0.34	0.41	0.30	0.28	0.30	0.33
$C_{12}$	0	0	0	0.30	0.32	0.37	0.35	0.36	0.36	0.32	0.39	0.34	0.32
$C_{13}$	0	0	0	0.31	0.31	0.32	0.26	0.30	0.23	0.38	0.33	0.36	0.35
$C_{21}$	0.43	0.35	0.35	0	0	0	0	0	0	0	0.29	0.35	0.32
$C_{22}$	0.29	0.36	0.35	0	0	0	0	0	0	0	0.37	0.34	0.32
$C_{23}$	0.29	0.29	0.29	0	0	0	0	0	0	0	0.34	0.32	0.36
$C_{31}$	0.20	0.28	0.27	0.26	0.27	0.25	0	0	0	0	0.28	0.29	0.24
$C_{32}$	0.24	0.25	0.23	0.23	0.24	0.21	0	0	0	0	0.24	0.24	0.28
$C_{33}$	0.29	0.26	0.25	0.26	0.27	0.25	0	0	0	0	0.24	0.26	0.23
$C_{34}$	0.26	0.22	0.25	0.25	0.22	0.29	0	0	0	0	0.25	0.22	0.25
$C_{41}$	0.36	0.38	0.34	0	0	0	0.36	0.32	0.35	0.39	0	0	0
$C_{42}$	0.35	0.33	0.37	0	0	0	0.37	0.37	0.36	0.37	0	0	0
$C_{43}$	0.30	0.28	0.29	0	0	0	0.27	0.31	0.29	0.24	0	0	0

after which, the weight calculation can be derived by the Equation (15) to a limit power. The process is continued until each row reaching a constant value.

Table 6. The final weights of criteria from the limited super-matrix.

	${\mathit{C}}_{11}$	${\mathit{C}}_{12}$	${\mathit{C}}_{13}$	${\mathit{C}}_{21}$	${\mathit{C}}_{22}$	${\mathit{C}}_{23}$	${\mathit{C}}_{31}$	${\mathit{C}}_{32}$	${\mathit{C}}_{33}$	${\mathit{C}}_{34}$	${\mathit{C}}_{41}$	${\mathit{C}}_{42}$	${\mathit{C}}_{43}$
DEMATEL and CFPR-ANP	0.128	0.127	0.116	0.058	0.056	0.051	0.065	0.059	0.064	0.060	0.077	0.078	0.061
Reasoning maps and CFPR-ANP	0.142	0.132	0.112	0.060	0.055	0.049	0.085	0.077	0.085	0.081	0.044	0.043	0.036

shows the weights of criteria after each row converged to a constant value. The probability of technical success (C₁₁) is deemed to be the most important criterion followed by the availability of R&D resources (C₁₂).

4.4. Using the COPRAS-G Method to Measure R&D Project Selection Levels

At present, the case company has five potential R&D projects under consideration. The managers involved come from different departments and their evaluation of each project varies because of their different backgrounds and viewpoints. The results of managerial evaluation cannot suitably be represented by a crisp number, rather they are expressed as an interval with lower and upper bounds (

Table 7. Evaluation results for the five R&D projects.

Criteria		${\mathit{C}}_{11}$	${\mathit{C}}_{12}$	${\mathit{C}}_{13}$	${\mathit{C}}_{21}$	${\mathit{C}}_{22}$	${\mathit{C}}_{23}$	${\mathit{C}}_{31}$	${\mathit{C}}_{32}$	${\mathit{C}}_{33}$	${\mathit{C}}_{34}$	${\mathit{C}}_{41}$	${\mathit{C}}_{42}$	${\mathit{C}}_{43}$
Weight		0.13	0.13	0.12	0.06	0.06	0.05	0.07	0.06	0.06	0.06	0.08	0.08	0.06
Project A	u	5.15	6.25	7.00	7.44	6.30	6.37	6.54	7.10	7.33	7.30	8.05	6.73	7.13
	l	3.19	4.86	5.11	5.67	4.70	4.41	4.58	4.90	5.67	5.37	5.95	4.71	5.98
Project B	u	9.30	9.08	7.46	7.94	8.44	8.70	9.56	9.65	9.17	9.43	8.56	9.85	9.27
	l	6.93	6.81	4.65	5.39	6.56	6.52	7.99	8.02	7.49	7.57	6.11	8.60	6.84
Project C	u	7.11	8.21	7.92	8.37	7.82	8.28	7.75	7.10	8.33	7.26	7.33	7.41	6.86
	l	5.44	6.79	6.30	6.63	6.29	6.38	5.92	5.46	6.67	5.74	5.67	6.04	4.91
Project D	u	7.26	7.27	7.48	7.65	7.70	7.54	6.16	6.85	7.54	6.80	7.23	6.61	6.58
	l	5.52	5.84	6.41	6.35	5.86	5.69	4.51	5.04	5.69	5.42	4.99	5.39	5.20
Project E	u	7.16	7.30	6.47	7.00	7.56	6.75	5.70	7.93	7.50	6.51	6.87	5.98	8.42
	l	5.17	5.03	4.53	4.22	5.55	4.36	3.08	5.73	5.17	4.49	4.46	3.35	6.80

). Using Equation (17), we can calculate the normalized decision-making matrix as shown in

Table 8. Normalized decision-making matrix $Q$ .

Criteria		${\mathit{C}}_{11}$	${\mathit{C}}_{12}$	${\mathit{C}}_{13}$	${\mathit{C}}_{21}$	${\mathit{C}}_{22}$	${\mathit{C}}_{23}$	${\mathit{C}}_{31}$	${\mathit{C}}_{32}$	${\mathit{C}}_{33}$	${\mathit{C}}_{34}$	${\mathit{C}}_{41}$	${\mathit{C}}_{42}$	${\mathit{C}}_{43}$
Weight		0.13	0.13	0.12	0.06	0.06	0.05	0.07	0.06	0.06	0.06	0.08	0.08	0.06
Project A	u	0.43	0.5	0.56	0.6	0.5	0.51	0.52	0.57	0.59	0.59	0.67	0.54	0.57
	l	0.35	0.42	0.43	0.46	0.41	0.4	0.41	0.42	0.46	0.45	0.48	0.41	0.48
Project B	u	0.87	0.83	0.6	0.65	0.72	0.76	0.93	0.95	0.84	0.9	0.74	1	0.86
	l	0.55	0.54	0.41	0.45	0.52	0.52	0.66	0.66	0.61	0.61	0.49	0.74	0.55
Project C	u	0.57	0.69	0.65	0.71	0.64	0.7	0.63	0.57	0.7	0.58	0.59	0.6	0.55
	l	0.45	0.54	0.5	0.53	0.5	0.51	0.48	0.45	0.53	0.47	0.46	0.49	0.42
Project D	u	0.58	0.58	0.6	0.62	0.63	0.61	0.49	0.55	0.61	0.54	0.58	0.53	0.52
	l	0.45	0.47	0.51	0.51	0.48	0.46	0.4	0.43	0.46	0.45	0.43	0.45	0.44
Project E	u	0.57	0.59	0.52	0.56	0.61	0.54	0.47	0.65	0.61	0.52	0.55	0.48	0.72
	l	0.44	0.43	0.4	0.39	0.46	0.4	0.35	0.47	0.44	0.4	0.4	0.36	0.54

. Then, combining the CFPR-ANP weights and following the steps of COPRAS-G, we can obtain the gray grade of the lower and upper bounds, the degree of utility and the final ranking for each project (

Table 9. Evaluation of the utility degree.

	$\mathit{\gamma }({\overline{\mathit{u}}}_{\mathit{j}}^{\mathit{a}\mathit{s}\mathit{p}\mathit{i}\mathit{r}\mathit{e}},\overline{{\mathit{u}}_{\mathit{k}\mathit{j}}})$	$\mathit{\gamma }({\overline{\mathit{u}}}_{\mathit{j}}^{\mathit{a}\mathit{s}\mathit{p}\mathit{i}\mathit{r}\mathit{e}},\overline{{\mathit{l}}_{\mathit{k}\mathit{j}}})$	${\mathit{V}}_{\mathit{k}}$	${\mathit{H}}_{\mathit{K}}\left(\mathit{\%}\right)$	Rank
Project A	0.54	0.43	0.48	70.6	5 (5)
Project B	0.81	0.56	0.68	100.0	1 (1)
Project C	0.63	0.49	0.56	81.6	2 (2)
Project D	0.57	0.46	0.52	75.6	3 (3)
Project E	0.56	0.42	0.49	71.9	4 (4)

Note: parentheses indicate the ranking from reasoning maps method.

). As shown in Table 9, project B, with a utility degree of 100%, is selected as the most suitable, Project C with a utility degree of 81.6% has the second priority. To explore the effects of different network structures in the R&D project selection, we applied the reasoning maps method [39] to construct a new network relationship map and conduct the analysis. The derived weights are different (Table 6) but the final ranking is the same (Table 9).

5. Discussion

R&D project selection is critical for a firm’s sustainability and future growth. The proposed model has the advantage of considering the interdependence of the evaluation criteria while building a network system. First, the DEMATEL method was used to construct the network structure of the super-matrix. The weights of the criteria were obtained by using a novel CFPR-ANP method, designed to remedy the shortcoming of the traditional ANP with its time-consuming pairwise comparisons. The interval values were adopted to represent the diverse managerial opinions. The opinions of experts are diverse due to many uncertain situations in the R&D project evaluating period. Using a crisp value to represent those various estimations might not be a proper way. A very popular method is using the fuzzy theory to represent the diverse opinions. The interval values with upper and lower bounds are easy applied and understandable for managers. The COPRAS-G method was applied to calculate the degree of utility of five potential R&D projects. The resultant priorities for R&D projects are B $\succ$ C $\succ$ D $\succ$ E $\succ$ A. The effectiveness and usefulness of the integrated model was demonstrated in an empirical example. Mangers can prioritize project execution based on the available resources and budgets. In addition to the above contributions, several management implications can be derived from the results.

A threshold value of 1.16 was adopted to construct the network relationship for DEMATEL network analysis. This number was agreed upon by managerial consensus, and appears to reflect the reality of this situation. A more complex network relationship could be obtained by reducing the value, but this would mean that more pairwise comparisons would be needed in the subsequent analysis. On the other hand, a higher value would reduce the complexity of the network system, but might not suitably represent real cases. Unfortunately, to the best of our knowledge, there is no systematic way to decide on this number. In this study, lower and higher threshold values were applied but without significantly changing the final weights in each criterion. According to the cause and effect INRM results (Figure 3), R&D and finance are deemed to be causative factors and manufacturing and marketing are considered as effect factors. The results suggest that within the R&D dimension these criteria should be carefully evaluated since they will affect the other criteria. These criteria include “probability of technical success”, “availability of R&D resources” and “applicability to other products and processes.” In addition, the financial criteria have to be considered because profitability and risk have to be considered for any projects started.

Table 6 shows the importance of the criteria. The results reveal that the probability of technical success (C₁₁), availability of R&D resources (C₁₂), and applicability to other products and processes (C₁₃) are the top three criteria with values of 12.8%, 12.7%, and 11.6%, respectively. The results are consistent with the INRM results. The probability of technical success is the most important issue in R&D development, because if the technology is beyond the capabilities of R&D personnel or the technology capability is not mature, the percentage of failure will be high. This high risk can be minimized by setting up an in-house R&D team for advance evaluation. The lowest priority factor is raw materials or components (C₂₃) at 5.1%. Inside the enterprise, material and component selection from a shared parts library is standard operation procedure. Once part selection has been approved, the firm will decide what is needed from the standard parts library ready. With such a mechanism, the chance of project failure is minimal. The rate of return on investment (C₄₂) is the most important criterion within the finance dimension. Profit is the ultimate goal for a firm to pursue, reflecting overall performance and efficiencies in terms of marketing, innovation, as well as productivity. In the dimension of marketing, the potential size of the market (C₃₁) is the most important factor to consider possible market size before the launch of a new project.

Currently, the case company has five potential projects under assessment. In the past, it has not been easy to reach a consensus due to differences of opinion. This problem has caused the development of too many products and a slow loss of the core competitiveness of the company. In this study, we applied interval values to represent the diverse opinions obtained during the project survey. The empirical example shows that this method could be an effective way to solve this type of problem. The interval values combined with the weights of the criteria can help to objectively prioritize the different projects. Then, based on the available resources and financial situation, the company can devise a strategy for the development of those projects. Our results indicate that projects B, C, D are the top three projects for initiation at the current stage.

We also made the comparisons between our proposed model and the COPRAS method [40,41,42,43,44,45]. The final ranking is the same but the relative significances are different. However, our model considered the decision makers’ uncertainty, which could be more reasonable in the current case study because the R&D projects are usually with some degrees of uncertainty or vagueness. If the evaluating values are certain crisp numbers, the COPRAS method should be a proper method.

6. Concluding Remarks

Over the past decade, rapid changes in the economy and technology have affected enterprises, which have limited resources. Incorrect R&D project selection could lead to a failure of innovation, loss of money and competitiveness, or, even worse, vanishing markets, meaning that innovation-oriented enterprises need an effective tool to assess and select the most appropriate R&D projects. We propose a hybrid model that considers the complex criteria and diverse opinions from various stakeholders and different departments for R&D project selection. The proposed hybrid model synthesizes the DEMATEL, CFPR-ANP and the COPRAS-G methods. The DEMATEL theory and CFPR-ANP are used to determine the weights of the R&D project selection evaluation criteria. The modified COPRAS-G method is applied to evaluate and select the best R&D projects. We present a case study of an international brand-name company to illustrate the applicability of our proposed framework.

Although the present study contributes to the body of R&D project selection, limitations remain. The derived conclusions are based on data from an electronics company; other markets might have different characteristics. Results should be validated using data from other industries. Another limitation is the lack of long-term data, for comparison with the current results. In summary, this study provides a new systematic approach for the R&D project selection problem that can be improved in future.