Effects of Percent Tree Canopy Density and DEM Misregistration on SRTM/NED Vegetation Height Estimates
Abstract
:1. Introduction
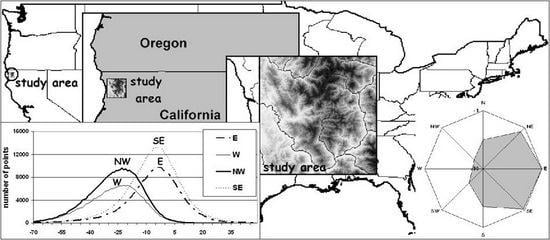
2. Study Area Data and Methodology
2.1. Data


2.2. Bare earth DEM, slope and aspect
2.3. SRTM finished DSM

2.4. Orthometric to geodetic height recalculation

2.5 Landcover and percent canopy density

3. Results and Discussion
3.1. Elevation differences modeling
| Terrain Class | Parameter | E | NE | N | NW | W | SW | S | SE |
|---|---|---|---|---|---|---|---|---|---|
| T O T A L | Points | 299,243 | 402,492 | 563,214 | 320,086 | 231,846 | 355,015 | 622,443 | 410,175 |
| Mean (m) | -5.9 | -8.2 | -17.7 | -26.7 | -27.2 | -23.5 | -14.2 | -6.1 | |
| st.dev.(m) | 14.8 | 14.1 | 13.9 | 13.8 | 14.6 | 14.3 | 14.9 | 14.7 | |
| kurtosis | 0.98 | 0.99 | 0.50 | 0.00 | 0.00 | 0.24 | 0.59 | 0.98 | |
| skew | -0.54 | -0.56 | -0.35 | -0.34 | -0.31 | -0.44 | -0.31 | -0.37 | |
| Canopy density <66 | points | 88,518 | 155,669 | 300,784 | 158,329 | 101,601 | 150,306 | 197,952 | 106,842 |
| Mean (m) | -1.1 | -3.8 | -15.4 | -23.6 | -24.6 | -20.1 | -11.1 | -2.0 | |
| st.dev.(m) | 13.4 | 12.7 | 13.4 | 13.3 | 14.0 | 13.4 | 14.1 | 14.0 | |
| kurtosis | 0.99 | 1.23 | 0.49 | 0.18 | 0.18 | 0.55 | 0.79 | 0.89 | |
| skew | -0.32 | -0.38 | -0.28 | -0.39 | -0.44 | -0.53 | -0.29 | -0.21 | |
| Canopy density >65 | points | 210,725 | 246,872 | 262,430 | 161,827 | 130,126 | 204,709 | 424,491 | 303,333 |
| Mean (m) | -7.9 | -9.9 | -20.2 | -28.8 | -29.2 | -26.0 | -15.7 | -7.6 | |
| st.dev (m) | 14.9 | 14.3 | 14.0 | 13.9 | 14.7 | 14.5 | 15.1 | 14.6 | |
| kurtosis | 1.16 | 1.12 | 0.44 | -0.11 | -0.03 | 0.13 | 0.52 | 0.99 | |
| Skew | -0.59 | -0.60 | -0.40 | -0.29 | -0.21 | -0.36 | -0.29 | -0.42 |



3.2. Elevation differences versus slope magnitude and percent tree canopy density


| Linear Regression | E | NE | N | NW | W | SW | S | SE | |
|---|---|---|---|---|---|---|---|---|---|
| Y = ( a * X ) + b | b | 9.9 | 6.8 | -6.5 | -16.6 | -16.8 | -10.8 | -4.6 | 7.2 |
| a | -0.214 | -0.214 | -0.173 | -0.152 | -0.152 | -0.185 | -0.124 | -0.17 | |
| slope= arctan(a)*180/π | -12.7 o | -12.7 o | -9.8 o | -8.7 o | -8.7 o | -10.5 o | -7.1 o | -9.7 o | |
| R2 | 0.92 | 0.91 | 0.97 | 0.97 | 0.97 | 0.95 | 0.84 | 0.90 | |
| Variance Ratio | 828.5 | 710.7 | 2546.2 | 2782.4 | 1357.0 | 1099.1 | 408.1 | 691.8 | |
3.3. Discussion
4. Conclusions
Acknowledgements
References and Notes
- Miliaresis, G.; Kokkas, N. Segmentation & Object Based Classification for the Extraction of Building Class from LIDAR DEMs. Comput. Geosci. 2007, 33, 1067–1087. [Google Scholar]
- Miliaresis, G. Quantification of Terrain Processes. Lecture Notes in Geoinformation & Chartography 2008, 14, 13–28. [Google Scholar]
- Osborn, K.; List, J.; Gesch, D.; Crowe, J.; Merril, G.; Constance, E.; Mauck, J.; Lund, C.; Caruso, V.; Kosovich, J. Digital Elevation Model Technologies and Applications, the DEM Users Manual; Maune, D., Ed.; American Society for Photogrammetry and Remote Sensing: Bethesda, MD, USA, 2001; Chapter 4; pp. 83–120. [Google Scholar]
- Rodriguez, E.; Morris, C.S.; Belz, J.E. A Global Assessment of the SRTM Performance. Photogramm. Eng. Remote Sens. 2006, 72, 249–261. [Google Scholar] [CrossRef]
- Kellndorfer, J.M.; Walker, W.S.; Pierce, L.E.; Dobson, M.C.; Fites, J.; Hunsaker, C.; Vona, J.; Clutter, M. Vegetation height derivation from Shuttle Radar Topography Mission and National Elevation data sets. Remote Sens. Environ. 2004, 93, 339–358. [Google Scholar] [CrossRef]
- Miliaresis, G.; Paraschou, Ch. Vertical Accuracy of the SRTM DTED Level 1 of Crete. Int. J. Appl. Earth Observ. GeoInfo. 2005, 7, 49–59. [Google Scholar] [CrossRef]
- Van Niel, T.G.; McVicar, T.R.; Li, L.T.; Gallant, J.C.; Yang, Q.K. The Impact of Misregistration on SRTM and DEM Image Differences. Remote Sens. Environ. 2008, 112, 2430–2442. [Google Scholar] [CrossRef]
- Braun, A.; Fotopoulos, G. Assessment of SRTM, ICESat, and Survey Control Monument Elevations in Canada. Photogramm. Eng. Remote Sens. 2007, 73, 1333–1342. [Google Scholar] [CrossRef]
- Bhang, K.J.; Schwartz, F.; Braun, A. Verification of the Vertical Error in C-Band SRTM DEM Using ICESat and Landsat-7, Otter Tail County, MN. IEEE Trans on Geosci. Remote Sens. 2007, 45, 36–44. [Google Scholar] [CrossRef]
- Carabajal, C.C.; Harding, D.J. ICESat Validation of SRTM C-band Digital Elevation Models. Geophys. Res. Lett. 2005, 32, L22S01. [Google Scholar] [CrossRef]
- Huang, C.; Yang, L.; Wylie, B.; Homer, C. A Strategy for Estimating Tree Canopy Density Using Landsat 7 ETM+ and High Resolution Images Over Large Areas. In 3rd Int. Conf. on Geospatial Information in Agriculture and Forestry; Denver, 5-7 November, 2001. http://landcover.usgs.gov/pdf/canopy_density.pdf.
- Homer, C.; Huang, C.; Yang, L.; Wylie, B.; Coan, M. Development of a 2001 National Landcover Database for the United States. Photogramm. Eng. Remote Sens. 2004, 70, 829–840. [Google Scholar] [CrossRef]
- Sircombe, K. AGEDispaly: an EXCEL Workbook to Evaluate and Display Univariate Geochronological Data Using Binned Frequency Histograms and Probability Density Distributions. Comput. Geosci. 2004, 30, 21–31. [Google Scholar] [CrossRef]
- Clark, W.; Hosking, P. Statistical Methods for Geographers; John Wiley & Sons: New York, NY, USA, 1986. [Google Scholar]
- Daniel, C.; Tennant, K. Digital Elevation Model Technologies and Applications, the DEM Users Manual; Maune, D., Ed.; American Society for Photogrammetry and Remote Sensing: Bethesda, 2001; Chapter 12; pp. 395–440. [Google Scholar]
- USGS Seamless Data Distribution System; 2007. http://seamless.usgs.gov/.
- Miliaresis, G. An Upland Object Based Modelling of the Vertical Accuracy of the SRTM-1 Elevation Dataset. J. Spatial Sci. 2007, 52, 13–29. [Google Scholar] [CrossRef]
- Florinsky, I. Derivation of Topographic Variables from a Digital Elevation Models Given by a Spheroidal Trapezoidal Grid. Int. J. Geogr. Info. Sci. 1998, 12, 829–852. [Google Scholar] [CrossRef]
- Farr, T.G.; Kobrick, M. Shuttle Radar Topography Mission Produces a Wealth of Data. Amer. Geophys. Union EOS 2000, 81, 583–585. [Google Scholar] [CrossRef]
- Slater, J.A.; Garvey, G; Johnston, C.; Haase, J.; Heady, B.; Kroenung, G.; Little, J. The SRTM Data “Finishing” Process and Products. Photogramm. Eng. Remote Sens. 2006, 72, 237–247. [Google Scholar] [CrossRef]
- Finished SRTM data. http://seamless.usgs.gov/website/seamless/faq/srtm_faq.asp2007.
- National Geospatial Agency. Technical Information page for USGG2003 and GEOID03; 2003. http://www.ngs.noaa.gov/GEOID/GEOID03/tech.html.
- Roman, D.R.; Wang, Y.M.; Henning, W.; Hamilton, J. Assessment of the New National Geoid Height Model, GEOID03. http://www.ngs.noaa.gov/pubs_lib/GEOID/ACSM04_GEOID03c.docIn Proceedings of the American Congress on Surveying and Mapping; Nashville Tennessee. 16-21 April, 2004.
- Lemoine, F.G.; Kenyon, J.K.; Factor, R.G.; Trimmer, N.K.; Pavlis, D.S.; Chinn, C.M.; Cox, S.M.; Klosko, S.B.; Luthcke, M.H.; Torrence, Y.M.; Wang, R.G.; Williamson, E.C.; Pavlis, R.H.; Rapp, T.R.; Olson, P. The Development of the Joint NASA GSFC and the NIMA Geopotential Model EGM96, NASA TP/-1998-206861; NASA Goddard Space Flight Center: Greenbelt, MD, 1999. [Google Scholar]
- Vogelmann, J.E.; Sohl, T.L.; Campbell, P.V.; Shaw, D.M. Regional Land Cover Characterization Using Landsat Thematic Mapper Data and Ancillary Data Sources. Environ. Monit. Assess. 1998, 51, 415–428. [Google Scholar] [CrossRef]
- Gorokhovich, Y.; Voustianiouk, A. Accuracy Assessment of the Processed SRTM Based Elevation Data by CGIAR Using Field Data from USA and Thailand and Its Relation to the Terrain Characteristics. Remote Sens. Environ. 2006, 104, 409–415. [Google Scholar] [CrossRef]
- Sun, G.; Ranson, K. J.; Kharuk, V. I.; Kovacs, K. Validation of Surface Height from Shuttle Radar Topography Mission using Shuttle Laser Altimeter. Remote Sens. Environ. 2003, 88, 401–411. [Google Scholar] [CrossRef]
© 2009 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Miliaresis, G.; Delikaraoglou, D. Effects of Percent Tree Canopy Density and DEM Misregistration on SRTM/NED Vegetation Height Estimates. Remote Sens. 2009, 1, 36-49. https://doi.org/10.3390/rs1020036
Miliaresis G, Delikaraoglou D. Effects of Percent Tree Canopy Density and DEM Misregistration on SRTM/NED Vegetation Height Estimates. Remote Sensing. 2009; 1(2):36-49. https://doi.org/10.3390/rs1020036
Chicago/Turabian StyleMiliaresis, George, and Demitris Delikaraoglou. 2009. "Effects of Percent Tree Canopy Density and DEM Misregistration on SRTM/NED Vegetation Height Estimates" Remote Sensing 1, no. 2: 36-49. https://doi.org/10.3390/rs1020036
APA StyleMiliaresis, G., & Delikaraoglou, D. (2009). Effects of Percent Tree Canopy Density and DEM Misregistration on SRTM/NED Vegetation Height Estimates. Remote Sensing, 1(2), 36-49. https://doi.org/10.3390/rs1020036