Ultrawideband Microwave Sensing and Imaging Using Time-Reversal Techniques: A Review
Abstract
:1. Introduction
2. Time-Reversal of Electromagnetic Waves and Superresolution


2.1. Physics-Based Ultrawideband Clutter Models
2.2. Numerical Results



3. Time-Reversal based Detection and Imaging Methods
3.1. Signal Space Methods
3.1.1. Time-Domain DORT

3.1.2. Space-Frequency TR Imaging
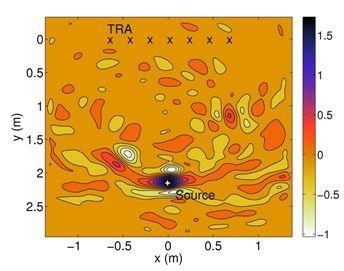
3.1.3. Results



3.2. Null Space Methods
3.2.1. TR-MUSIC


4. Frequency Dispersion/Loss Compensation Techniques





5. Conclusions
Acknowledgements
References and Notes
- Varshney, P.K. Distributed Detection and Data Fusion; Springer-Verlag: Berlin, Germany, 1997. [Google Scholar]
- Paulraj, A.J.; Gore, D.A.; Nabar, R.U.; Bolcskei, H. An overview of MIMO communications–a key to gigabit wireless. Proc. IEEE 2004, 92, 198–218. [Google Scholar] [CrossRef]
- Foschini, G.J.; Gans, M.J. On limits of wireless communication in a fading environment when using multiple antennas. Wirel. Personal Commun. 1998, 6, 311–335. [Google Scholar] [CrossRef]
- Fink, M.; Cassereau, D.; Derode, A.; Prada, C.; Roux, P.; Tanter, M.; Thomas, J.; Wu, F. Time-reversed acoustics. Rep. Prog. Phys. 2000, 63, 1933–1995. [Google Scholar] [CrossRef]
- Fink, M. Method and device for localization and focusing of acoustic waves in tissues. US Patent 5,092,336, 1992. [Google Scholar]
- Fink, M. Method and apparatus for acoustic examination using time reversal. US Patent 5,428,999, 1995. [Google Scholar]
- Fink, M.; Lewiner, J. Method and device for detecting and locating a reflecting sound source. US Patent 6,161,434, 2000. [Google Scholar]
- Berryman, J.G.; Borcea, L.; Papanicolaou, G.; Tsogka, C. Statistically stable ultrasonic imaging in random media. J. Acoust. Soc. Am. 2002, 112, 1509–1522. [Google Scholar] [CrossRef] [PubMed]
- Papanicolaou, G.; Ryzhik, L.; Solna, K. Statistical stability in time reversal. SIAM J. Appl. Math. 2004, 64, 1133–55. [Google Scholar] [CrossRef]
- Fouque, J.-P.; Garnier, J.; Papanicolaou, G.; Solna, K. Wave Propagation and Time Reversal in Randomly Layered Media; Springer: Berlin, Germany, 2007. [Google Scholar]
- Fink, M. Time reversal mirrors. J. Phys. D.: Appl. Phys. 1993, 26, 1333–1350. [Google Scholar] [CrossRef]
- Clouet, J.F.; Fouque, J.P. A time reversal method for an acoustical pulse propagating in randomly layered media. Wave Motion 1997, 25, 361–368. [Google Scholar] [CrossRef]
- Dowling, D.R.; Jackson, D.R. Narrowband performance of phase conjugate arrays in dynamic random media. J. Acoust. Soc. Am. 1992, 91, 3257–3277. [Google Scholar] [CrossRef]
- Asch, M.; Kohler, W.; Papanicolaou, G.; Postel, M.; White, B. Frequency content of randomly scattered signals. SIAM Review 1991, 33, 519–62. [Google Scholar] [CrossRef]
- Kohler, W.; Papanicolaou, G.; White, B. Localization and mode conversion for elastic waves in randomly layered media. Wave Motion 1996, 23, 1–22 and 181–201. [Google Scholar] [CrossRef]
- Borcea, L.; Papanicolaou, G.; Tsogka, C.; Berryman, J. Imaging and time reversal in random media. Inverse Prob. 2002, 18, 1247–1279. [Google Scholar] [CrossRef]
- Tsogka, C.; Papanicolaou, G. Time reversal through a solid-liquid interface and super-resolution. Inverse Prob. 2002, 18, 1639–1657. [Google Scholar] [CrossRef]
- Blomgren, P.; Papanicolaou, G.; Tsogka, C.; Berryman, J. Super resolution in time-reversal acoustics. J. Acoust. Soc. Am. 2002, 111, 230–48. [Google Scholar] [CrossRef] [PubMed]
- Chan, T.; Jaruwatanadilok, S.; Kuga, Y.; Ishimaru, A. Numerical study of the time-reversal effects on super-resolution in random scattering media and comparison with an analytical mode. Waves in Random and Complex Media 2008, 18, 627–639. [Google Scholar] [CrossRef]
- Montaldo, G.; Roux, P.; Derode, A.; Negreira, C.; Fink, M. Ultrasonic shock wave generator using 1-bit time-reversal in a dispersive medium : application to lithotripsy. Appl. Phys. Lett. 2002, 80, 897–899. [Google Scholar] [CrossRef]
- Thomas, J.L.; Wu, F.; Fink, M. Time reversal focusing applied to lithotripsy. Ultrason. Imag. 1996, 18, 106–121. [Google Scholar] [CrossRef]
- Tanter, M.; Thomas, J.L.; Fink, M. Focusing and steering through absorbing and aberrating layers: Application to ultrasonic propagation through the skull. J. Acoust. Soc. Am. 1998, 103, 2403–2410. [Google Scholar] [CrossRef] [PubMed]
- Floch, C.L.; Tanter, M.; Fink, M. Self defocusing in ultrasonic hyperthermia: Experiment and simulation. Appl. Phys. Lett. 1999, 74, 3062–3064. [Google Scholar] [CrossRef]
- Persson, M.; Trefna, H. Method and system relating to hyperthermia. World Intellectual Property Organization - International Patent Application Publication Application number: PCT/SE2007/000502, Publication No: WO/2007/136335, 2007. [Google Scholar]
- Pepper, D.M.; Dunning, G.J.; Sumida, D.S. Time-reversed photoacoustic system and uses thereof. US Patent 6,973,830, 2005. [Google Scholar]
- Cerwin, S.A.; Chang, D.B. Identifying and treating bodily tissues using electromagnetically induced, time-reversed, acoustic signals. United States Patent Application Publication Application number: 11/450,097, US 2007/0038060 A1, 2007. [Google Scholar]
- Ihn, J.-B.; Dunne, J.P. Virtual time reversal acoustics for structural health monitoring. United States Patent Application Publication Application number: 11/861,056, US 2009/0083004 A1, 2007. [Google Scholar]
- Larmat, C.; Tromp, T.; Liu, Q.; Montagner, J.-P. Time reversal location of glacial earthquakes. J. Geophys. Res. B 2008, 113, B09314. [Google Scholar] [CrossRef]
- Micolau, G.; Saillard, M.; Borderies, P. DORT method as applied to ultrawideband signals for detection of buried objects. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1813–1820. [Google Scholar] [CrossRef]
- Edelmann, G.F.; Song, H.C.; Kim, S.; Akal, T.; Hodgkiss, W.S.; Kuperman, W.A. Underwater acoustic communications using time reversal. IEEE J.Oceanic Eng. 2005, 30, 852–864. [Google Scholar] [CrossRef]
- Higley, W.J.; Roux, P.; Kuperman, W.A.; Hodgkiss, W.S.; Song, H.C.; Akal, T.; Stevenson, M. Synthetic aperture time-reversal communications in shallow water: Experimental demonstration at sea. J. Acoust. Soc. Am. 2005, 118, 2365–2372. [Google Scholar] [CrossRef]
- Kim, S.; Kuperman, W.A.; Hodgkiss, W.S.; Song, H.C.; Edelman, G.F.; Akal, T. Echo-to-reverberation enhancement using a time reversal mirror. J. Acoust. Soc. Am. 2004, 115, 1525–1531. [Google Scholar] [CrossRef]
- Song, H.C.; Hodgkiss, W.S.; Kuperman, W.A.; Roux, P.; Akal, T.; Stevenson, M. Experimental demonstration of adaptive reverberation nulling using time reversal. J. Acoust. Soc. Am. 2005, 118, 1382–1387. [Google Scholar] [CrossRef]
- Milsap, J.P. Phased array sound system. US Patent 7,130,430, 2006. [Google Scholar]
- Leutenegger, T.; Dual, J. Non-destructive testing of tubes using a time reverse numerical simulation (TRNS) method. Ultrasonics 2004, 41, 811–822. [Google Scholar] [CrossRef] [PubMed]
- Kerbrat, E.; Prada, C.; Cassereau, D. Ultrasonic nondestructive testing of scattering media using the decomposition of the time-reversal operator. IEEE T. Ultrason. Ferroelectr. 2002, 49, 1103–1112. [Google Scholar] [CrossRef]
- Leutenegger, T.; Dual, J. Detection of defects in cylindrical structures using a time reverse method and a finite-difference approach. Ultrasonics 2002, 40, 721–725. [Google Scholar] [CrossRef]
- Chakroun, N.; Fink, M.; Wu, F. Time reversal processing in ultrasonic nondestructive testing. IEEE T. Ultrason. Ferroelectr. 1995, 42, 1087–1098. [Google Scholar] [CrossRef]
- Sohn, H.; Kim, S. Methods, apparatuses, and systems for damage detection. World Intellectual Property Organization - International Patent Application Publication Application number: PCT/US2007/015090, Publication No: WO/2008/005311, 2008. [Google Scholar]
- Lev-Ari, H.; Devaney, A.J. The Time Reversal Techniques Re-interpreted: Subspace-based Signal Processing for Multistatic Target Location. In Proceedings of IEEE Sensor Array and Multichannel Signal Processing Workshop, Cambridge, MA, USA; 2000; pp. 509–513. [Google Scholar]
- Hou, S.; Solna, K.; Zhao, H. Imaging of location and geometry for extended targets using the response matrix. J. Comp. Phys. 2004, 199, 317–338. [Google Scholar] [CrossRef]
- Borcea, L.; Papanicolaou, G.; Tsogka, C. Theory and applications of time reversal and interferometric imaging. Inverse Prob. 2003, 19, 1–26. [Google Scholar] [CrossRef]
- Borcea, L.; Papanicolaou, G.; Tsogka, C. Interferometric array imaging in clutter. Inverse Prob. 2005, 21, 1419–1460. [Google Scholar] [CrossRef]
- Slob, E. Interferometry by deconvolution of multicomponent multioffset gpr data. IEEE Trans. Geosci. Remote Sens. 2009, 47, 828–838. [Google Scholar] [CrossRef]
- Derveaux, G.; Papanicolaou, G.; Tsogka, C. Time reversal imaging for sensor networks with optimal compensation in time. J. Acoust. Soc. Am. 2007, 121, 2071–2085. [Google Scholar] [CrossRef] [PubMed]
- Prada, C.; Fink, M. Eigenmodes of the time reversal operator: A solution to selective focusing in multiple-target media. Wave Motion 1994, 20, 151–163. [Google Scholar] [CrossRef]
- Prada, C.; Mannevile, S.; Spoliansky, D.; Fink, M. Decomposition of the time reversal operator: Detection and selective focusing on two scatterers. J. Acoust. Soc. Am. 1996, 99, 2067–2076. [Google Scholar] [CrossRef]
- Prada, C.; Thomas, J.L. Experimental subwavelength localization of scatterers by decomposition of the time reversal operator interpreted as a covariance matrix. J. Acoust. Soc. Am. 2003, 114, 235–243. [Google Scholar] [CrossRef] [PubMed]
- Micolau, G.; Saillard, M. DORT method as applied to electromagnetic sensing of buried objects. Radio Sci. 2003, 38, 4–1–12. [Google Scholar] [CrossRef]
- Montaldo, G.; Tanter, M.; Fink, M. Real time inverse filter focusing through iterative time reversal. J. Acoust. Soc. Am. 2004, 115, 768–775. [Google Scholar] [CrossRef] [PubMed]
- Montaldo, G.; Tanter, M.; Fink, M. Revisiting iterative time reversal processing: Application to detection of multiple targets. J. Acoust. Soc. Am. 2004, 115, 776–784. [Google Scholar] [CrossRef] [PubMed]
- Devaney, A.J. Super-resolution processing of multistatic data using time reversal and MUSIC. Unpublished paper, preprint available on the author’s web site. Avalable Online: http://www.ece.neu.edu/faculty/devaney/ (accessed on August 20, 2009).
- Gruber, F.K.; Marengo, E.A.; Devaney, A.J. Time-reversal imaging with multiple signal classification considering multiple scattering between the targets. J. Acoust. Soc. Am. 2004, 115, 3042–3047. [Google Scholar] [CrossRef]
- Marengo, E.A.; Gruber, F.K. Subspace-based localization and inverse scattering of multiply scattering point targets. EURASIP J. Adv. Signal Proc. 2007. [Google Scholar] [CrossRef]
- Lehman, S.K.; Devaney, A.J. Transmission mode time-reversal superresolution imaging. J. Acoust. Soc. Am. 2003, 113, 2742–2753. [Google Scholar] [CrossRef] [PubMed]
- Devaney, A.J.; Marengo, E.A.; Gruber, F.K. Time-reversal-based imaging and inverse scattering of multiply scattering point targets. J. Acoust. Soc. Am. 2005, 118, 3129–3138. [Google Scholar] [CrossRef]
- Devaney, A.J. Time reversal imaging of obscured targets from multistatic data. IEEE Trans. Antennas Propagat. 2005, 53, 1600–1610. [Google Scholar] [CrossRef]
- Pepper, D.M. Nonlinear optical phase conjugation. Optical Engineer. 1982, 21, 156. [Google Scholar]
- Byren, R.W.; Rockwell, D.A. Self-aligning phase conjugate laser. US Patent 4,812,639, 1989. [Google Scholar]
- Byren, R.W.; Filgas, D. Phase conjugate relay mirror apparatus for high energy laser system and method. US Patent 6,961,171, 2005. [Google Scholar]
- Skolnik, M.I.; King, D.D. Self-Phasing array antennas. IEEE Trans. Antennas Propagat. 1964, 12, 142–149. [Google Scholar] [CrossRef]
- Sichelstiel, B.A.; Waters, W.M.; Wild, T.A. Self-Focusing array research model. IEEE Trans. Antennas Propagat. 1964, 12, 150–154. [Google Scholar] [CrossRef]
- Fusco, V.F.; Karode, S.L. Self-Focusing antenna array techniques for mobile communications applications. Elect. & Comm. Eng. J. 1999, 11, 279–286. [Google Scholar]
- Chang, Y.; Fetterman, H.R.; Newberg, I.L.; Panaretos, S.K. Microwave phase conjugation using antenna arrays. IEEE Trans. Microwave Theory Tech. 1998, 46, 1910–1919. [Google Scholar] [CrossRef]
- Miyamoto, R.Y.; Itoh, T. Retrodirective arrays for wireless communications. IEEE Microwave Magazine 2002, 3, 71–79. [Google Scholar] [CrossRef]
- Henty, B.E.; Stancil, D.D. Multipath-enabled super-resolution for rf and microwave communication using phase-conjugate arrays. Phys. Rev. Lett. 2004, 93, 243904/1–4. [Google Scholar] [CrossRef] [PubMed]
- Lerosey, G.; de Rosny, J.; Tourin, A.; Derode, A.; Montaldo, G.; Fink, M. Time reversal of electromagnetic waves. Phys. Rev. Lett. 2004, 92, 193904. [Google Scholar] [CrossRef] [PubMed]
- Lerosey, G.; de Rosny, J.; Tourin, A.; Derode, A.; Fink, M. Time reversal of wideband microwaves. Applied Phys. Lett. 2006, 88. [Google Scholar] [CrossRef]
- Cepni, A.G. Experimental Investigation of Time-Reversal Techniques using Electromagnetic Waves. Ph D. Dissertation, Carnegie Mellon University, Pittsburgh, PA, USA, 2005. [Google Scholar]
- Nguyen, H.T.; Andersen, J.B.; Pedersen, G.F.; Kyritsi, P.; Eggers, P.C.F. Time reversal in wireless communications: A measurement-based investigation. IEEE Trans. Wireless Comm. 2006, 5, 2242–2252. [Google Scholar] [CrossRef]
- Moura, J.M.F.; Jin, Y. Detection by time reversal: Single antenna. IEEE Trans. Signal Process. 2007, 55, 187–201. [Google Scholar] [CrossRef]
- Moura, J.M.F.; Jin, Y.W. Time reversal imaging by adaptive interference canceling. IEEE Trans. Signal Process. 2008, 56, 233–247. [Google Scholar] [CrossRef]
- Jin, Y.; Moura, J.M.F. Time-reversal detection using antenna arrays. IEEE Trans. Signal Process. 2009, 57, 1396–1414. [Google Scholar]
- Li, X.; Bond, E.J.; Veen, B.D.V.; Hagness, S.C. An overview of ultra-wideband microwave imaging via space-time beamforming for early-stage breast-cancer detection. IEEE Antennas Propagat. Mag. 2005, 47, 19–34. [Google Scholar]
- Kosmas, P.; Rappaport, C.M. Time reversal with the FDTD method for microwave breast cancer detection. IEEE Trans. Microwave Theory Tech. 2005, 53, 2317–2323. [Google Scholar] [CrossRef]
- Kosmas, P. FDTD modeling for forward and linear inverse electromagnetic problems in lossy, dispersive media. Ph. D. Dissertation, Northeastern University, Boston, MA, USA, 2005. [Google Scholar]
- Kosmas, P.; Rappaport, C.M. FDTD-based time reversal for microwave breast cancer detection - localization in three dimensions. IEEE Trans. Microwave Theory Tech. 2006, 54, 1921–1927. [Google Scholar] [CrossRef]
- Kosmas, P.; Rappaport, C.M. A matched-filter FDTD-based time reversal approach for microwave breast cancer detection. IEEE Trans. Antennas Propagat. 2006, 54, 1257–1264. [Google Scholar] [CrossRef]
- Chen, Y.F.; Gunawan, E.; Low, K.S.; Wang, S.C.; Kim, Y.; Soh, C.B. Pulse design for time reversal method as applied to ultrawideband microwave breast cancer detection: A two-dimensional analysis. IEEE Trans. Antennas Propagat. 2007, 55, 194–204. [Google Scholar] [CrossRef]
- Chen, Y.F.; Gunawan, E.; Low, K.S.; Wang, S.C.; Soh, C.B.; Putti, T.C. Time-reversal ultrawideband breast imaging: Pulse design criteria considering multiple tumors with unknown tissue properties. IEEE Trans. Antennas Propagat. 2008, 56, 3073–3077. [Google Scholar] [CrossRef]
- Jin, Y.; Moura, J.M.F.; Jiang, Y.; Wahl, M.; Zhu, H.; He, Q. Breast cancer detection by time reversal imaging. In Proceedings of 5th IEEE International Symposium on Biomedical Imaging: From Nano to Macro (ISBI), Paris, France, May 14-17, 2008; pp. 816–819.
- Liu, D.H.; Kang, G.; Li, L.; Chen, Y.; Vasudevan, S.; Joines, W.; Liu, Q.H.; Krolik, J.; Carin, L. Electromagnetic time-reversal imaging of a target in a cluttered environment. IEEE Trans. Antennas Propagat. 2005, 53, 3058–3066. [Google Scholar]
- Liu, D.H.; Vasudevan, S.; Krolik, J.; Bal, G.; Carin, L. Electromagnetic time-reversal source localization in changing media: Experiment and analysis. IEEE Trans. Antennas Propagat. 2007, 55, 344–354. [Google Scholar] [CrossRef]
- Liu, D.H.; Krolik, J.; Carin, L. Electromagnetic target detection in uncertain media: Time-reversal and minimum-variance algorithms. IEEE Trans. Geosci. Remote Sens. 2007, 45, 934–944. [Google Scholar] [CrossRef]
- Tortel, H.; Micolau, G.; Saillard, M. Decomposition of the time reversal operator for electromagnetic scattering. J. Electromagn. Waves Appl. 1999, 13, 687–719. [Google Scholar] [CrossRef]
- Chambers, D.H.; Berryman, J.G. Analysis of the time-reversal operator for a small spherical scatterer in an electromagnetic field. IEEE Trans. Antennas Propagat. 2004, 52, 1729–1738. [Google Scholar] [CrossRef]
- Berryman, J.G. Method for distinguishing multiple targets using time-reversal acoustics. US Patent 6,755,083, 2004. [Google Scholar]
- Sarabandi, K.; Koh, I.; Casciato, M.D. Demonstration of time reversal methods in a multi-path environment. Proceedings of the IEEE Antennas and Propagation Society International Symposium 2004, 4, 4436–4439. [Google Scholar]
- Ziade, Y.; Roussel, H.; Lesturgie, M.; Tabbara, W. A coherent model of forest propagation–application to detection and localization of targets using the DORT method. IEEE Trans. Antennas Propagat. 2008, 56, 1048–1057. [Google Scholar] [CrossRef]
- Jiang, Y.; Zhu, J.; Stancil, D.D.; Chabalko, M.J. Polarization sensitive time-reversal SAR imaging in an environment filled with trees. Proc. of the IEEE Antennas Propagat. Symp. 2007, 1, 4000–4003. [Google Scholar]
- Jiang, Y.; Zhu, J.; Stancil, D.D. Synthetic aperture radar ghost image cancellation using broadband time reversal averaging techniques. IEEE/MTT-S Int. Microwave Symposium 2007, 1479–1482. [Google Scholar] [CrossRef]
- Jin, Y.; Moura, J.M.F. Application of time reversal to synthetic aperture imaging. United States Patent Application Publication Application number: 12/217,839, US 2009/0033549 A1, 2008. [Google Scholar]
- Jin, Y.; Moura, J.M.F. Imaging by time reversal beamforming. United States Patent Application Publication Application number: 12/217,838, US 2009/0076389 A1, 2009. [Google Scholar]
- Zheng, W.; Zhao, Z.; Nie, Z.P. Application of TRM in the UWB through wall radar. Prog. Electromagnetics Res. - PIER 2008, 87, 279–296. [Google Scholar] [CrossRef]
- Kyritsi, P.; Papanicolaou, G.; Eggers, P.; Oprea, A. MISO time reversal and delay-spread compression for FWA channels at 5 GHz. IEEE Antennas Wirel. Prop. Lett. 2004, 3, 96–99. [Google Scholar] [CrossRef]
- Lerosey, G.; de Rosny, J.; Tourin, A.; Derode, A.; Montaldo, G.; Fink, M. Time reversal of electromagnetic waves and telecommunication. Radio Sci. 2005, 40. [Google Scholar] [CrossRef]
- Montaldo, G.; Lerosey, G.; Derode, A.; Tourin, A.; de Rosny, J.; Fink, M. Telecommunication in a disordered environment with iterative time reversal. Waves in Random Media 2004, 14, 287–302. [Google Scholar] [CrossRef]
- Xiao, S.Q.; Chen, J.; Wang, B.Z.; Liu, X.F. A numerical study on time-reversal electromagnetic wave for indoor ultra-wideband signal transmission. Prog. Electromagnetics Res. - PIER 2007, 77, 329–342. [Google Scholar] [CrossRef]
- Blomgren, P.; Kyritsi, P.; Kim, A.D.; Papanicolaou, G. Spatial focusing and intersymbol interference in multiple-input-single-output time reversal communication systems. IEEE J. Oceanic Eng. 2008, 33, 341–355. [Google Scholar] [CrossRef]
- Lindskog, E.D.; Paulraj, A.J. Time-reversal block transmit diversity system for channels with intersymbol interference and method. US Patent 7,362,815, 2008. [Google Scholar]
- Candy, J.V.; Chambers, D.H.; Guidry, B.L.; Poggio, A.J.; Robbins, C.L. Multi-channel time-reversal receivers for multi and 1-bit implementations. US Patent 7,463,690, 2008. [Google Scholar]
- Pajusco, P.; Pagani, P. On the use of uniform circular arrays for characterizing UWB time reversal. IEEE Trans. Antennas Propagat. 2009, 57, 102–109. [Google Scholar] [CrossRef]
- Coppinger, F.; Bhushan, A.S.; Jalali, B. Time reversal of broadband microwave signals. Electron. Lett. 1999, 35, 1230–1232. [Google Scholar] [CrossRef]
- Yanik, M.F.; Suh, W.; Wang, Z.; Fan, S. Stopping and time reversing light in a waveguide with an all-optical system. US Patent 7,116,864, 2006. [Google Scholar]
- Yavuz, M.E.; Teixeira, F.L. A numerical study of time reversed UWB electromagnetic waves in continuous random media. IEEE Antennas Wirel.Prop. Lett. 2005, 4, 43–46. [Google Scholar] [CrossRef]
- Yavuz, M.E.; Teixeira, F.L. Full time-domain DORT for ultrawideband fields in dispersive, random inhomogeneous media. IEEE Trans. Antennas Propagat. 2006, 54, 2305–2315. [Google Scholar] [CrossRef]
- Yavuz, M.E.; Teixeira, F.L. Space-frequency ultrawideband time-reversal imaging. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1115–1124. [Google Scholar] [CrossRef]
- Yavuz, M.E.; Teixeira, F.L. On the sensitivity of time-reversal imaging techniques to model perturbations. IEEE Trans. Antennas Propagat. 2008, 56, 834–843. [Google Scholar] [CrossRef]
- Yavuz, M.E.; Teixeira, F.L. Frequency dispersion compensation in time reversal techniques for UWB electromagnetic waves. IEEE Geosci. Remote Sensing Lett. 2005, 2, 233–237. [Google Scholar] [CrossRef]
- Born, M.; Wolf, E. Principles of Optics; Academic Press: New York, NY, USA, 1970. [Google Scholar]
- Fung, A.K.; Fung, H.S. Scattering from a vegetation layer. IEEE Trans. Geosci. Electron. 1979, 17, 1–6. [Google Scholar] [CrossRef]
- Tsang, L.; Kong, J.A. Thermal microwave emission from a three-layer random medium with three dimensional variations. IEEE Trans. Geosci. Remote Sens. 1980, 18, 212–216. [Google Scholar] [CrossRef]
- Wang, J.R.; Shiue, J.C.; Chuang, S.L.; Shin, R.T.; Dobrowski, M. Thermal microwave emission from vegetated fields: A comparison between theory and experiment. IEEE Trans. Geosci. Remote Sens. 1984, 22, 143–149. [Google Scholar] [CrossRef]
- Moss, C.D.; Teixeira, F.L.; Yang, Y.E.; Kong, J.A. Finite-difference time-domain simulation of scattering from objects in continuous random media. IEEE Trans. Geosci. Remote Sens. 2002, 40, 178–186. [Google Scholar] [CrossRef]
- Berenger, J.P. A perfectly matched layer for the absorption of electromagnetic waves. J. Comput. Phys. 1994, 114, 185–200. [Google Scholar] [CrossRef]
- Teixeira, F.L.; Chew, W.C. A general approach to extended berenger’s absorbing boundary condition to anisotropic and dispersive media. IEEE Trans. Antennas Propagat. 1998, 46, 1386–1387. [Google Scholar] [CrossRef]
- Harris, F.J. On the use of windows for harmonic analysis with the discrete fourier transform. Proc. IEEE 1978, 66, 51–83. [Google Scholar] [CrossRef]
- Prada, C.; Wu, F.; Fink, M. The iterative time reversal mirror: A solution to self-focusing in the pulse echo mode. J. Acoust. Soc. Am. 1991, 90, 1119–1129. [Google Scholar] [CrossRef]
- Yavuz, M.E. Time reversal based signal processing techniques for ultrawideband electromagnetic sensing in random media. Ph. D. Dissertation, The Ohio State University, Columbus, OH, USA, 2008. [Google Scholar]
- Yavuz, M.E.; Teixeira, F.L. Time Reversal Based Signal Processing Techniques: Algorithms and Applications on Ultrawideband Electromagnetic Remote Sensing; VDM Verlag: Saarbrucken, Germany, 2009. [Google Scholar]
- Scholz, B. Towards virtual electrical breast biopsy: Space-frequency MUSIC for trans-admittance data. IEEE Trans. Med. Imag. 2002, 21, 588–595. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.S.; Li, J.; Wu, R.B. Time-delay- and time-reversal-based robust capon beamformers for ultrasound imaging. IEEE Tran. Medical Imag. 2005, 24, 1308–1322. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, D.Q.; Wan, W.S. Novel DORT method in non-well-resolved scatterer case. IEEE Signal Proc. Lett. 2008, 15, 705–708. [Google Scholar] [CrossRef]
- Zhao, H. Analysis of the response matrix for an extended target. SIAM J. Appl. Math. 2004, 64, 725–745. [Google Scholar] [CrossRef]
- Yavuz, M.E.; Teixeira, F.L. Effects of array restriction on time-reversal methods. Proc. of the 2007 IEEE Antennas Prop. Symp. 2007. [Google Scholar] [CrossRef]
- Marengo, E.A.; Gruber, F.K.; Simonetti, F. Time-reversal MUSIC imaging of extended targets. IEEE Trans. Image Processing 2007, 16, 1967–1984. [Google Scholar] [CrossRef]
- Baussard, A.; Boutin, T. Time-reversal RAP-MUSIC imaging. Waves in Random and Complex Media 2008, 18, 151–160. [Google Scholar] [CrossRef]
- Folégot, T.; Prada, C.; Fink, M. Resolution enhancement and separation of reverbaration from target echo with the time reversal operator decomposition. J. Acoust. Soc. Am. 2003, 113, 3155–3160. [Google Scholar] [CrossRef] [PubMed]
- Saillard, M.; Vincent, P.; Micolau, G. Reconstruction of buried objects surrounded by small inhomogeneities. Inverse Prob. 2000, 16, 1195–1208. [Google Scholar] [CrossRef]
- Pozar, D.M. Microwave Engineering, 2nd ed.; John Wiley & Sons: New York, NY, USA, 1998. [Google Scholar]
- Teixeira, F.L.; Chew, W.C.; Straka, M.; Oristaglio, M.L.; Wang, T. Finite-difference time-domain simulation of ground penetrating radar on dispersive, inhomogeneous and conductive soils. IEEE Trans. Geosci. Remote Sensing 1998, 36, 1928–1937. [Google Scholar] [CrossRef]
- Oppenheim, A.; Schafer, R.W. Discrete-Time Signal Processing; Prentice Hall: Upper Saddle River, NJ, USA, 1999. [Google Scholar]
© 2009 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Yavuz, M.E.; Teixeira, F.L. Ultrawideband Microwave Sensing and Imaging Using Time-Reversal Techniques: A Review. Remote Sens. 2009, 1, 466-495. https://doi.org/10.3390/rs1030466
Yavuz ME, Teixeira FL. Ultrawideband Microwave Sensing and Imaging Using Time-Reversal Techniques: A Review. Remote Sensing. 2009; 1(3):466-495. https://doi.org/10.3390/rs1030466
Chicago/Turabian StyleYavuz, Mehmet Emre, and Fernando L. Teixeira. 2009. "Ultrawideband Microwave Sensing and Imaging Using Time-Reversal Techniques: A Review" Remote Sensing 1, no. 3: 466-495. https://doi.org/10.3390/rs1030466
APA StyleYavuz, M. E., & Teixeira, F. L. (2009). Ultrawideband Microwave Sensing and Imaging Using Time-Reversal Techniques: A Review. Remote Sensing, 1(3), 466-495. https://doi.org/10.3390/rs1030466