An Approach to Improve the Positioning Performance of GPS/INS/UWB Integrated System with Two-Step Filter
Abstract
:1. Introduction
2. GPS/INS/UWB Tightly Coupled Navigation
2.1. System State Model
2.2. Observation Model
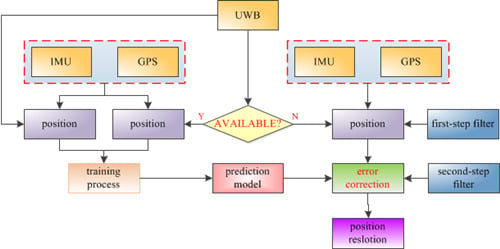
3. Position Error Correction under UWB Outages Conditions
3.1. Position Error Prediction with UWB Observation
3.2. Position Error Correction Scheme with Two-Step Filter
4. Field Test and Analysis
- Stage one: The UWB signal is available and GPS, INS and UWB are integrated from 486,300 s to 486,500 s.
- Stage two: The UWB signal is unavailable and GPS and INS are integrated without error correction from 486,500 s to 486,700 s.
- Stage three: The UWB signal is unavailable and GPS and INS are integrated with error correction scheme presented in Section 3 from 486,700 s to 486,900 s.
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Nassar, S.; El-Sheimy, N. A combined algorithm of improving INS error modeling and sensor measurements for accurate INS/GPS navigation. GPS Solut. 2006, 10, 29–39. [Google Scholar] [CrossRef]
- Teunissen, P.; Odolinski, R.; Odijk, D. Instantaneous BeiDou+GPS RTK positioning with high cut-off elevation angles. J. Geod. 2014, 88, 335–350. [Google Scholar] [CrossRef]
- Odolinski, R.; Teunissen, P.J.; Odijk, D. Combined BDS, Galileo, QZSS and GPS single-frequency RTK. GPS Solut. 2015, 19, 151–163. [Google Scholar] [CrossRef]
- Wübbena, G.; Schmitz, M.; Bagge, A. PPP-RTK: Precise point positioning using state-space representation in RTK networks. In Proceedings of the 18th International Technical Meeting of the Satellite Division of The Institute of Navigation, Long Beach, CA, USA, 13–16 September 2005. [Google Scholar]
- Teunissen, P.; Khodabandeh, A. Review and principles of PPP-RTK methods. J. Geod. 2015, 89, 217–240. [Google Scholar] [CrossRef]
- Li, X.; Zhang, X.; Ge, M. Regional reference network augmented precise point positioning for instantaneous ambiguity resolution. J. Geod. 2011, 85, 151–158. [Google Scholar] [CrossRef]
- Geng, J.; Teferle, F.N.; Meng, X.; Dodson, A. Towards PPP-RTK: Ambiguity resolution in real-time precise point positioning. Adv. Space Res. 2011, 47, 1664–1673. [Google Scholar] [CrossRef]
- Kubo, N.; Hou, R.; Suzuki, T. Decimeter level vehicle navigation combining multi-GNSS with existing sensors in dense urban areas. In Proceedings of the 2014 International Technical Meeting of The Institute of Navigation, San Diego, CA, USA, 27–29 January 2014. [Google Scholar]
- MacGougan, G.; O’Keefe, K. Real time UWB error estimation in a tightly-coupled GPS/UWB positioning system. In Proceedings of the 2009 International Technical Meeting of The Institute of Navigation, Anaheim, CA, USA, 26–28 January 2009. [Google Scholar]
- MacGougan, G.; O’Keefe, K.; Chiu, D. Multiple UWB range assisted GPS RTK in hostile environments. In Proceedings of the 21st International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS 2008), Savannah, GA, USA, 16–19 September 2008. [Google Scholar]
- MacGougan, G.; O’Keefe, K.; Klukas, R. Accuracy and reliability of tightly coupled GPS/ultra-wideband positioning for surveying in urban environments. GPS Solut. 2010, 14, 351–364. [Google Scholar] [CrossRef]
- De Angelis, A.; Nilsson, J.; Skog, I.; Händel, P.; Carbone, P. Indoor positioning by ultrawide band radio aided inertial navigation. Metrol. Meas. Syst. 2010, 17, 447–460. [Google Scholar] [CrossRef]
- MacGougan, G.; O’Keefe, K.; Klukas, R. Tightly-coupled GPS/UWB integration. J. Navig. 2010, 63, 1–22. [Google Scholar] [CrossRef]
- Jiang, Y.; Petovello, M.; O’Keefe, K.; Basnayake, C. Augmentation of carrier-phase DGPS with UWB ranges for relative vehicle positioning. In Proceedings of the 25th International Technical Meeting of The Satellite Division of the Institute of Navigation (ION GNSS 2012), Nashville, TN, USA, 17–21 September 2012. [Google Scholar]
- Petovello, M.G.; O’Keefe, K.; Chan, B.; Spiller, S.; Pedrosa, C.; Xie, P.; Basnayake, C. Demonstration of inter-vehicle UWB ranging to augment DGPS for improved relative positioning. J. Glob. Position Syst. 2012, 11, 11–21. [Google Scholar] [CrossRef]
- Wang, D.; O’Keefe, K.; Petovello, M.G. Decentralized cooperative navigation for vehicle-to-vehicle (V2V) applications using GPS integrated with UWB range. In Proceedings of the ION 2013 Pacific PNT Meeting, Honolulu, HI, USA, 23–25 April 2013. [Google Scholar]
- Gross, J.N.; Yu, G. Dewberry Brandon Tightly-coupled GPS/UWB-ranging for relative navigation during formation flight. In Proceedings of the 27th International Technical Meeting of The Satellite Division of the Institute of Navigation (ION GNSS+ 2014), Tampa, FL, USA, 8–12 September 2014. [Google Scholar]
- Gao, Y.; Meng, X.; Hancock, C.M.; Stephenson, S.; Zhang, Q. UWB/GNSS-based cooperative positioning method for V2X applications. In Proceedings of the 27th International Technical Meeting of The Satellite Division of the Institute of Navigation (ION GNSS+ 2014), Tampa, FL, USA, 8–12 September 2014. [Google Scholar]
- Dierenbach, K.; Ostrowski, S.; Jozkow, G.; Toth, C.K.; Grejner-Brzezinska, D.A.; Koppanyi, Z. UWB for Navigation in GNSS Compromised Environments. In Proceedings of the 28th International Technical Meeting of The Satellite Division of the Institute of Navigation (ION GNSS+ 2015), Tampa, FL, USA, 14–18 September 2015. [Google Scholar]
- Tanigawa, M.; Hol, J.D.; Dijkstra, F.; Luinge, H.; Slycke, P. Augmentation of low-cost GPS/MEMS INS with UWB positioning system for seamless outdoor/indoor positioning. In Proceedings of the 21st International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS 2008), Savannah, GA, USA, 16–19 September 2008. [Google Scholar]
- Vydhyanathan, A.; Luinge, H.; Tanigawa, M.; Dijkstra, F.; Braasch, M.S.; de Haag, M.U. Augmenting low-cost GPS/INS with ultra-wideband transceivers for multi-platform relative navigation. In Proceedings of the 22nd International Technical Meeting of The Satellite Division of the Institute of Navigation (ION GNSS 2009), Savannah, GA, USA, 22–25 September 2009. [Google Scholar]
- Ascher, C.; Zwirello, L.; Zwick, T.; Trommer, G. Integrity monitoring for UWB/INS tightly coupled pedestrian indoor scenarios. In Proceedings of the 2011 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Guimaraes, Portugal, 21–23 September 2011. [Google Scholar]
- Shen, F.; Cheong, J.W.; Dempster, A.G. An ultra-wide bandwidth-based range/GPS tight integration approach for relative positioning in vehicular ad hoc networks. Meas. Sci. Technol. 2015, 26, 045003. [Google Scholar] [CrossRef]
- Li, Z.; Wang, J.; Li, B.; Gao, J.; Tan, X. GPS/INS/Odometer integrated system using fuzzy neural network for land vehicle navigation applications. J. Navig. 2014, 67, 967–983. [Google Scholar] [CrossRef]
- Angrisano, A. GNSS/INS Integration Methods. Ph.D. Thesis, The University of Calgary, Calgary, AB, Canada, 2010. [Google Scholar]
- Yao, Y.; Xu, X.; Zhu, C.; Chan, C.Y. A hybrid fusion algorithm for GPS/INS integration during GPS outages. Measurement 2017, 103, 42–51. [Google Scholar] [CrossRef]
- Wang, J.; Gao, Y.; Li, Z.; Meng, X.; Hancock, C.M. A tightly-coupled GPS/INS/UWB cooperative positioning sensors system supported by V2I communication. Sensors 2016, 16, 944. [Google Scholar] [CrossRef] [PubMed]
- Stephenson, S.; Meng, X.; Moore, T.; Baxendale, A.; Edwards, T. Precision of network real time kinematic positioning for intelligent transport systems. In Proceedings of the European Navigation Conference, London, UK, 29 November–1 December 2011. [Google Scholar]

















| Parameters | Gyroscope | Accelerometer |
|---|---|---|
| Initial bias error | ±0.25°/s | ±0.002 g |
| In-run bias stability | 18°/h | ±0.04 mg |
| Scale factor stability | ±0.05% | ±0.05% |
| Random walk | 0.03°/s/sqrt (Hz) | 80 µg/sqrt (Hz) |
| Scheme | RMS (m) | MEAN (m) | ||||
|---|---|---|---|---|---|---|
| North | East | Down | North | East | Down | |
| GPS/INS/UWB | 0.36 | 0.11 | 0.56 | 0.19 | −0.01 | −0.38 |
| GPS/INS | 2.00 | 0.89 | 0.65 | 1.83 | 0.74 | −0.46 |
| Scheme | RMS (m) | MEAN (m) | ||
|---|---|---|---|---|
| North | East | North | East | |
| Error correction | 0.89 | 0.42 | 0.57 | −0.15 |
| GPS/INS | 1.70 | 0.55 | 1.62 | 0.45 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Wang, R.; Gao, J.; Wang, J. An Approach to Improve the Positioning Performance of GPS/INS/UWB Integrated System with Two-Step Filter. Remote Sens. 2018, 10, 19. https://doi.org/10.3390/rs10010019
Li Z, Wang R, Gao J, Wang J. An Approach to Improve the Positioning Performance of GPS/INS/UWB Integrated System with Two-Step Filter. Remote Sensing. 2018; 10(1):19. https://doi.org/10.3390/rs10010019
Chicago/Turabian StyleLi, Zengke, Ren Wang, Jingxiang Gao, and Jian Wang. 2018. "An Approach to Improve the Positioning Performance of GPS/INS/UWB Integrated System with Two-Step Filter" Remote Sensing 10, no. 1: 19. https://doi.org/10.3390/rs10010019
APA StyleLi, Z., Wang, R., Gao, J., & Wang, J. (2018). An Approach to Improve the Positioning Performance of GPS/INS/UWB Integrated System with Two-Step Filter. Remote Sensing, 10(1), 19. https://doi.org/10.3390/rs10010019