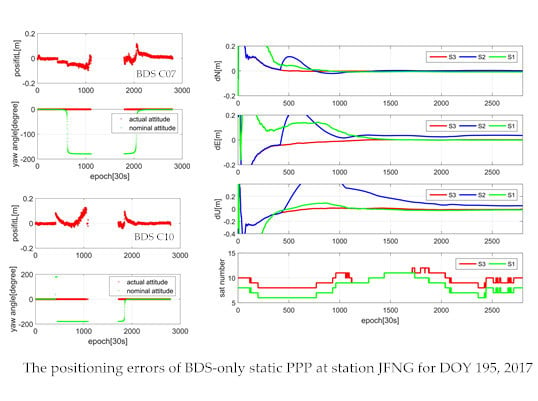
2.1. The Attitude Model for GNSS Satellites
The nominal yaw angle
can be computed by the sun angle
(the elevation angle of the sun above the orbital plane [
23], −90°–90°) and the orbit angle
(the geocentric angle between the sun and orbit midnight, growing with the satellite motion, 0–360°):
where the function atan2(y, x) in C/C++ returns the principal value of the arc tangent of y/x, expressed in radians (in the interval
). According to the current IGS convention, the unit vector of sun and the
X-axis direction of the yaw-steering frame are always pointing towards the same hemisphere, including GPS IIR and GALILEO satellites [
3]. Therefore, Equation (1) is used for all GNSS satellites to calculate the nominal yaw angles and the sign of
is opposite to that of
.
Ignoring the small time variation of the sun angle
, the yaw rate
can be derived as follows:
where
denotes the orbital angular velocity. According to the orbital period, the average orbital angular velocities for GNSS are summarized in
Table 1. Substituting
and the maximum hardware yaw rate
R into Equation (2), the approximate maximum sun angle limit
can be expressed as follows:
where the function atan(x) in C/C++ returns the arc tangent of x, expressed in radians (in the interval
). For GPS II/IIA satellites, the averaged JPL reprocessing yaw-rate solutions during 1996–2008 [
24] are provided, with the average value of 0.1176°/s (0.0815°/s–0.1401°/s). The average hardware yaw rate for GPS IIR, GPS IIF and GLONASS-M satellites are 0.20°/s, 0.11°/s and 0.25°/s, respectively. Different from GPS and GLONASS satellites, the GALILEO (IOV and FOC) and BDS (IGSO and MEO) satellites adopt the fixed threshold values. Then, the sun angle limits of noon maneuver are showed in the second column of
Table 2. Only when the satellite moves to near the noon and
, it will experience noon maneuver or switch to orbit normal mode (BDS MEO and IGSO satellites).
Different from the noon maneuver, as soon as the satellite enters into the shadow regime, the solar sensors of some satellites are unable to perceive the position of the sun. According to the mean radius of earth and the altitude of the satellite orbit, the average sun angle limits for shadow crossing regime are shown in the third column of
Table 2. It is noteworthy that only the midnight maneuver is considered during the shadow crossing regime for GPS IIR and GALILEO (IOV and FOC) satellites. At this time, a smaller value of
causes a shorter period of shadow crossing. Except for GPS II/IIA satellites, there is no post-shadow recovery for other satellite types, including GPS IIF satellites. It is recommended to delete the 30 min of data for GPS II/IIA satellites after the exit of shadow crossing.
Different from GPS/GLONASS/GALILEO satellites, BDS satellites adopt the yaw steering mode and orbit normal mode. It is important to know the attitude switching time because of the big differences of yaw angle between these two attitude modes (the yaw angle is always 0 for orbit normal mode). Considering that the yaw angle cannot complete an abrupt change in a short time, the preliminary attitude switch model, established by Dai et al. [
12], is adopted in this contribution:
The condition for YS- > ON: (1) and ; or (2) and when .
The condition for ON- > YS: (1) and ; or (2) and when .
When the satellite enters into the noon maneuver or shadow crossing regime, the actual yaw angle can be modeled according to different attitude models [
5,
6,
9,
10,
12]. In this contribution, the process of the acceleration of hardware yaw angle during the noon maneuver and the shadow crossing is ignored. The details and the results of the modeled yaw angles in this contribution are shown in
Section 3.2.
When the satellites enter into the eclipsing regimes, if the nominal yaw angle is used instead of the actual one, the induced-errors of the wind-up effect and antenna PCO will deteriorate the positioning accuracy, especially when is small. These errors, especially the antenna PCO, can also be reflected in the phase observation residuals.
2.2. The Multi-GNSS Precise Point Positioning and Its Strategy
The traditional PPP model adopts Ionosphere-Free (IF) combinations to eliminate the first-order ionospheric delays, which amounts to ignoring the spatial and temporal characteristics of the ionospheric delays. The corresponding observations of dual-frequency IF combinations are presented as follows:
where
(m) and
(m) are the observed-minus-computed pseudorange and phase observables after correcting necessary errors for satellite s and receiver r, respectively; the superscript “sys” denotes satellite system according to RINEX version 3.03 [
25] (G = GPS, R = GLONASS, E = GALILEO, C = BDS);
is the linearized vector from satellite s to receiver r and
(m) is the coordinate increment vector with respect to the priori value;
(m) is the zenith tropospheric wet delay for receiver r and
is its corresponding mapping function;
(m) and
(m) are the frequency-independent clock offsets for receiver
r and satellite
s, respectively;
denotes the wavelength;
(cycle) is the float ambiguity due to the assimilation of the hardware delays;
(m) is the satellite PCO correction which influences both the pseudorange and phase observables, while the wind-up correct
(m) only influences the phase observables;
(m) and
(m) are the pseudorange hardware delays of the IF combination for receiver
r and satellite
s, respectively;
(m) and
(m) are the phase hardware delays of the IF combination for receiver
r and satellite
s, respectively; and
(m) and
(m) are the unmodeled errors in the pseudorange and phase observables, respectively. Without considering the pseudorange Inter-Frequency Biases (IFBs) of GLONASS, the pseudorange hardware delays of receiver can be treated as satellite-independent [
26]. During the subsequent derivation,
is used instead of
.
To solve the rank deficiency caused by the correlations between the clock parameters and hardware delays, in general, the new reparameterized clock is defined:
at this time, the pseudorange hardware delays absorbed into the clock parameters are introduced to the phase observations. Therefore, the new float ambiguity parameters
can be expressed as the linear combination of the ambiguities and the hardware delays:
Instead of estimating one receiver clock for one satellite system, an alternative method is to introduce Inter-System Biases (ISBs) to compensate for the time differences among GNSS and GPS is selected as the reference in the GNSS PPP processing.
where the superscript “*” denotes the abbreviation for satellite systems. The estimable ISBs parameters not only contain the true system time differences, but also the differences of hardware delays of the IF combinations. Eventually, the full rank GNSS PPP model using IF combinations are obtained:
When multi-GNSS data are available, the prior variance of observations are given as follows [
27]:
where
e is the satellite elevation. The value of
for GPS/GALILEO can be set as 0.003 m and 0.3 m for the raw pseudorange and phase observables, respectively. Due to the neglect of the pseudorange IFBs, the value of
for GLONASS pseudorange observables is enlarged by several times [
26], such as 0.9 m. The phase IFBs of GLONASS can be absorbed by the GLONASS float ambiguities; therefore, the value of
for GLONASS phase observables can be set as the same as that of GPS [
26]. For BDS GEO satellites, because of the low accuracy of the orbit and clock products, the value of
for GEO can be set as 1.2 m and 0.009 m for the raw pseudorange and phase observables [
27,
28]. Due to the satellite-induced code variations for BDS IGSO and MEO satellites, the value of
for IGSO/MEO can be set as 0.4 m after correcting the satellite-induced code errors using the linear interpolation model [
29]. The phase observables of IGSO and MEO satellites are not influenced by these errors and the value of
for IGSO/MEO phase observables can also be set as the same as that of GPS [
27].
During the data pre-processing, data integrity, pseudorange gross errors [
30] and cycle-slips [
31] are checked and detected. When cycle slip occurs, new ambiguity parameters are introduced into the filter state rather than being repaired. However, the pre-processing is difficult to detect the small cycle-slips and code gross errors. To reduce the influence of the undetected cycle slips and gross errors, the robust Kalman filter using IGG (Institute of Geodesy and Geophysics) III function [
32] based on the observation residuals is used to adjust the variance of the observations:
where
is the equivalent variance and
is the variance inflation factor;
is the standardized residual; and
and
are the threshold, which are usually chosen as 1.5 and 3.0, respectively. For each iteration, only the satellite with the maximum standardized residual is selected to adjust its variance. When the standardized residual of phase observable is bigger than
, the ambiguity of this satellite is reset as a new parameter, rather than setting its variance as a large value.
The strategy of GNSS PPP is summarized in
Table 3. Multi-GNSS precise orbit and clock products from GFZ/Wuhan University are used. Due to the small higher-order ionospheric delays, the higher-order corrections are ignored in all PPP schemes. Currently, the phase center corrections of receiver for GALILEO and BDS are still unavailable. Therefore, the corrections of receiver PCO and PCV (Phase Center Variations) for GALILEO and BDS are assumed the same as that of GPS. After fixing the orbit, clock and DCBs for all visible satellites, the estimable parameters for GNSS PPP are
. The process noise of the Kalman filter state is also shown in
Table 3.