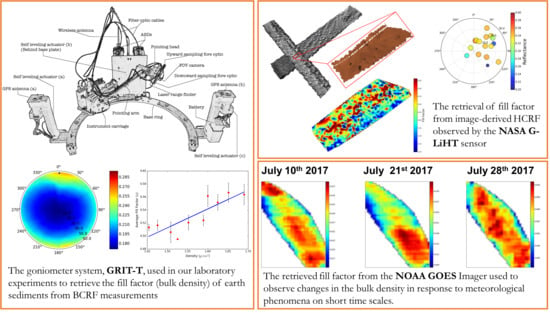
Retrieval of Sediment Fill Factor by Inversion of a Modified Hapke Model Applied to Sampled HCRF from Airborne and Satellite Imagery
Abstract
:1. Introduction
2. Study Area
3. Theoretical Development
3.1. BRDF: Theoretical Background
3.2. Hapke IMSA Model
3.3. Shadow-Hiding Opposition Effect
3.4. Modified Hapke IMSA Model
3.5. Inversion Methodology
4. Laboratory Studies
4.1. GRIT-T: Design and Instrumentation
4.2. Laboratory Measurements
4.3. Spectral Analysis and Fill Factor Retrieval
5. NASA Goddard’s LiDAR, Hyperspectral, and Thermal (G-LiHT) Airborne Imager
5.1. G-LiHT: Design and Instrumentation
5.2. Spectral Analysis and Fill Factor Retrieval from G-LiHT Imagery
6. The Geostationary Operational Environmental Satellite (GOES)
6.1. GOES: Design and Instrumentation
6.2. Spectral Analysis and Fill Factor Retrieval from GOES Imagery
7. Monitoring Large-Scale Changes in the Sand Dunes
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ben-Dor, E.; Chabrillat, S.; Demattê, J.; Taylor, G.; Hill, J.; Whiting, M.; Sommer, S. Using imaging spectroscopy to study soil properties. Remote Sens. Environ. 2009, 113, S38–S55. [Google Scholar] [CrossRef]
- Gaber, A.; Soliman, F.; Koch, M.; El-Baz, F. Using full-polarimetric SAR data to characterize the surface sediments in desert areas: A case study in El-Gallaba Plain, Egypt. Remote Sens. Environ. 2015, 162, 11–28. [Google Scholar] [CrossRef]
- Bachmann, C.M.; Eon, R.S.; Ambeau, B.; Harms, J.; Badura, G.; Griffo, C. Modeling and intercomparison of field and laboratory hyperspectral goniometer measurements with G-LiHT imagery of the Algodones Dunes. J. Appl. Remote Sens. 2017, 12. [Google Scholar] [CrossRef]
- Bachmann, C.M.; Philpot, W.; Abelev, A.; Korwan, D. Phase angle dependence of sand density observable in hyperspectral reflectance. Remote Sens. Environ. 2014, 150, 53–65. [Google Scholar] [CrossRef]
- Hapke, B. Theory of Reflectance and Emittance Spectroscopy; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Helfenstein, P.; Shepard, M.K. Testing the Hapke photometric model: Improved inversion and the porosity correction. Icarus 2011, 215, 83–100. [Google Scholar] [CrossRef]
- Sadeghi, M.; Babaeian, E.; Tuller, M.; Jones, S.B. Particle size effects on soil reflectance explained by an analytical radiative transfer model. Remote Sens. Environ. 2018, 210, 375–386. [Google Scholar] [CrossRef]
- Dematte, J.; Nanni, M.; da Silva, A.; de Melo Filho, J.; Dos Santos, W.; Campos, R. Soil density evaluated by spectral reflectance as an evidence of compaction effects. Int. J. Remote Sens. 2010, 31, 403–422. [Google Scholar] [CrossRef]
- Horn, R.; Rostek, J. Subsoil compaction processes-state of knowledge. Adv. GeoEcol. 2000, 32, 44–54. [Google Scholar]
- Schjønning, P.; Lamandé, M.; Keller, T.; Pedersen, J.; Stettler, M. Rules of thumb for minimizing subsoil compaction. Soil Use Manag. 2012, 28, 378–393. [Google Scholar] [CrossRef]
- Soane, B.; Van Ouwerkerk, C. Implications of soil compaction in crop production for the quality of the environment. Soil Tillage Res. 1995, 35, 5–22. [Google Scholar] [CrossRef]
- Lipiec, J.; Hatano, R. Quantification of compaction effects on soil physical properties and crop growth. Geoderma 2003, 116, 107–136. [Google Scholar] [CrossRef]
- Miller, I. Soil degradation in Eastern Canada: Its extent and impact. Can. J. Agric. Econ./Revue Can. D’agroecon. 1985, 33, 7–18. [Google Scholar] [CrossRef]
- Oldeman, L.; Hakkeling, R.; Sombroek, W.G. World Map of the Status of Human-Induced Soil Degradation: An Explanatory Note; International Soil Reference and Information Centre: Wageningen, The Netherlands, 2017.
- Da Silva, A.P.; Kay, B.; Perfect, E. Management versus inherent soil properties effects on bulk density and relative compaction. Soil Tillage Res. 1997, 44, 81–93. [Google Scholar] [CrossRef]
- Wang, Z.; Coburn, C.A.; Ren, X.; Teillet, P.M. Effect of surface roughness, wavelength, illumination, and viewing zenith angles on soil surface BRDF using an imaging BRDF approach. Int. J. Remote Sens. 2014, 35, 6894–6913. [Google Scholar] [CrossRef]
- Anderson, K.; Croft, H. Remote sensing of soil surface properties. Prog. Phys. Geogr. 2009, 33, 457–473. [Google Scholar] [CrossRef]
- Labarre, S.; Ferrari, C.; Jacquemoud, S. Surface roughness retrieval by inversion of the Hapke model: A multiscale approach. Icarus 2017, 290, 63–80. [Google Scholar] [CrossRef]
- Wu, Y.; Gong, P.; Liu, Q.; Chappell, A. Retrieving photometric properties of desert surfaces in China using the Hapke model and MISR data. Remote Sens. Environ. 2009, 113, 213–223. [Google Scholar] [CrossRef]
- Yang, G.J.; Zhao, C.J.; Huang, W.J.; Wang, J.H. Extension of the Hapke bidirectional reflectance model to retrieve soil water content. Hydrol. Earth Syst. Sci. 2011, 15, 2317–2326. [Google Scholar] [CrossRef] [Green Version]
- Pinty, B.; Verstraete, M.M.; Dickinson, R.E. A physical model for predicting bidirectional reflectances over bare soil. Remote Sens. Environ. 1989, 27, 273–288. [Google Scholar] [CrossRef]
- Cierniewski, J. A model for soil surface roughness influence on the spectral response of bare soils in the visible and near-infrared range. Remote Sens. Environ. 1987, 23, 97–115. [Google Scholar] [CrossRef]
- Cooper, K.D.; Smith, J.A. A Monte Carlo reflectance model for soil surfaces with three-dimensional structure. IEEE Trans. Geosci. Remote Sens. 1985, GE-23, 668–673. [Google Scholar] [CrossRef]
- Karnieli, A.; Cierniewski, J. Inferring the roughness of desert rocky surfaces from their bidirectional reflectance data. Adv. Space Res. 2001, 28, 171–176. [Google Scholar] [CrossRef] [Green Version]
- Deering, D.; Eck, T.; Otterman, J. Bidirectional reflectances of selected desert surfaces and their three-parameter soil characterization. Agric. For. Meteorol. 1990, 52, 71–93. [Google Scholar] [CrossRef]
- Chappell, A.; Zobeck, T.M.; Brunner, G. Using bi-directional soil spectral reflectance to model soil surface changes induced by rainfall and wind-tunnel abrasion. Remote Sens. Environ. 2006, 102, 328–343. [Google Scholar] [CrossRef]
- Chappell, A.; Strong, C.; McTainsh, G.; Leys, J. Detecting induced in situ erodibility of a dust-producing playa in Australia using a bi-directional soil spectral reflectance model. Remote Sens. Environ. 2007, 106, 508–524. [Google Scholar] [CrossRef]
- Kolokolova, L.; Liu, L.; Buratti, B.; Mishchenko, M.I. Modeling variations in near-infrared spectra caused by the coherent backscattering effect. J. Quant. Spectrosc. Radiat. Transf. 2011, 112, 2175–2181. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Baret, F.; Hanocq, J. Modeling spectral and bidirectional soil reflectance. Remote Sens. Environ. 1992, 41, 123–132. [Google Scholar] [CrossRef]
- Eon, R.S.; Gerace, A.D.; Montanaro, M.; Ambeau, B.L.; McCorkel, J.T. Development of a simulation environment to support intercalibration studies over the Algodones Dunes system. J. Appl. Remote Sens. 2017, 12, 012008. [Google Scholar] [CrossRef]
- Goodenough, A.A.; Brown, S.D. DIRSIG 5: Core design and implementation. Proc. SPIE 2012, 8390. [Google Scholar] [CrossRef]
- Hapke, B. Bidirectional reflectance spectroscopy: 6. Effects of porosity. Icarus 2008, 195, 918–926. [Google Scholar] [CrossRef]
- Bachmann, C.M.; Abelev, A.; Montes, M.J.; Philpot, W.; Gray, D.; Doctor, K.Z.; Fusina, R.A.; Mattis, G.; Chen, W.; Noble, S.C.; et al. A flexible goniometer system: The Goniometer for Outdoor Portable Earth Reflectance (GOPHER). J. Appl. Remote Sens. 2016, 10. [Google Scholar] [CrossRef]
- Georgiev, G.T.; Gatebe, C.K.; Butler, J.J.; King, M.D. BRDF analysis of savanna vegetation and salt-pan samples. IEEE Trans. Geosci. Remote Sens. 2009, 47, 2546–2556. [Google Scholar] [CrossRef]
- Capaccioni, F.; Cerroni, P.; Barucci, M.; Fulchignoni, M. Phase curves of meteorites and terrestrial rocks: Laboratory measurements and applications to asteroids. Icarus 1990, 83, 325–348. [Google Scholar] [CrossRef]
- Näränen, J.; Kaasalainen, S.; Peltoniemi, J.; Heikkilä, S.; Granvik, M.; Saarinen, V. Laboratory photometry of planetary regolith analogs-II. Surface roughness and extremes of packing density. Astron. Astrophys. 2004, 426, 1103–1109. [Google Scholar] [CrossRef]
- Shepard, M.K.; Helfenstein, P. A test of the Hapke photometric model. J. Geophys. Res. 2007, 112. [Google Scholar] [CrossRef] [Green Version]
- Bachmann, C.M.; Peck, D.S.; Ambeau, B.; Harms, J.; Schultz, M. Improved modeling of multiple scattering in hyperspectral BRDF of coastal sediments observed using the Goniometer of the Rochester Institute of Technology (GRIT). Proc. SPIE 2015. [Google Scholar] [CrossRef]
- McCorkel, J.; Bachmann, C.M.; Coburn, C.; Gerace, A.D.; Leigh, L.; Czapla-Myers, J.S.; Helder, D.L.; Cook, B.D. Overview of the 2015 Algodones sand dunes field campaign to support sensor intercalibration. J. Appl. Remote Sens. 2017, 12. [Google Scholar] [CrossRef]
- Cook, B.D.; Nelson, R.F.; Middleton, E.M.; Morton, D.C.; McCorkel, J.T.; Masek, J.G.; Ranson, K.J.; Ly, V.; Montesano, P.M. NASA Goddard’s LiDAR, hyperspectral and thermal (G-LiHT) airborne imager. Remote Sens. 2013, 5, 4045–4066. [Google Scholar] [CrossRef]
- Harms, J.D.; Bachmann, C.M.; Ambeau, B.L.; Faulring, J.W.; Torres, A.J.R.; Badura, G.; Myers, E. Fully automated laboratory and field-portable goniometer used for performing accurate and precise multiangular reflectance measurements. J. Appl. Remote Sens. 2017, 11. [Google Scholar] [CrossRef]
- Schmit, T.J.; Gunshor, M.M.; Menzel, W.P.; Gurka, J.J.; Li, J.; Bachmeier, A.S. Introducing the next-generation Advanced Baseline Imager on GOES-R. Bull. Am. Meteorol. Soc. 2005, 86, 1079–1096. [Google Scholar] [CrossRef]
- Luckenbach, R.A.; Bury, R.B. Effects of off-road vehicles on the biota of the Algodones Dunes, Imperial County, California. J. Appl. Ecol. 1983, 20, 265–286. [Google Scholar] [CrossRef]
- Norris, R.M.; Norris, K.S. Algodones dunes of southeastern California. Geol. Soc. Am. Bull. 1961, 72, 605–619. [Google Scholar] [CrossRef]
- Smith, R.S.; Yeend, W.; Dohrenwend, J.; Gese, D. Mineral Resources of the North Algodones Dunes Wilderness Study Area (CDCA-360), Imperial County, California; Technical Report; Geological Survey: Menlo Park, CA, USA; Bureau of Mines: Denver, CO, USA, 1984.
- Helder, D.; Thome, K.J.; Mishra, N.; Chander, G.; Xiong, X.; Angal, A.; Choi, T. Absolute radiometric calibration of Landsat using a pseudo invariant calibration site. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1360–1369. [Google Scholar] [CrossRef]
- Coburn, C.A.; Logie, G.S.J. Temporal dynamics of sand dune bidirectional reflectance characteristics for absolute radiometric calibration of optical remote sensing data. J. Appl. Remote Sens. 2017, 12. [Google Scholar] [CrossRef]
- Nicodemus, F.E.; Richmond, J.C.; Hsia, J.J. Geometrical Considerations and Nomenclature for Reflectance; US Department of Commerce, National Bureau of Standards: Washington, DC, USA, 1977; Volume 160.
- Schaepman-Strub, G.; Schaepman, M.; Painter, T.; Dangel, S.; Martonchik, J. Reflectance quantities in optical remote sensing—Definitions and case studies. Remote Sens. Environ. 2006, 103, 27–42. [Google Scholar] [CrossRef]
- Milton, E. Review article principles of field spectroscopy. Remote Sens. 1987, 8, 1807–1827. [Google Scholar] [CrossRef]
- Hapke, B.; Wells, E. Bidirectional reflectance spectroscopy: 2. Experiments and observations. J. Geophys. Res.: Solid Earth 1981, 86, 3055–3060. [Google Scholar] [CrossRef]
- Hapke, B. Bidirectional reflectance spectroscopy: 1. Theory. J. Geophys. Res.: Solid Earth 1981, 86, 3039–3054. [Google Scholar] [CrossRef]
- Hapke, B. Bidirectional reflectance spectroscopy: 5. The coherent backscatter opposition effect and anisotropic scattering. Icarus 2002, 157, 523–534. [Google Scholar] [CrossRef]
- Hapke, B. Bidirectional reflectance spectroscopy: 4. The extinction coefficient and the opposition effect. Icarus 1986, 67, 264–280. [Google Scholar] [CrossRef]
- Helfenstein, P.; Veverka, J.; Hillier, J. The lunar opposition effect: A test of alternative models. Icarus 1997, 128, 2–14. [Google Scholar] [CrossRef]
- Hapke, B.; Nelson, R.; Smythe, W. The opposition effect of the moon: Coherent backscatter and shadow hiding. Icarus 1998, 133, 89–97. [Google Scholar] [CrossRef]
- Nelder, J.A.; Mead, R. A simplex method for function minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- Badura, G.P.; Bachmann, C.M.; Tyler, A.C.; Goldsmith, S.; Eon, R.S.A. A Novel Approach for Deriving LAI of Salt Marsh Vegetation Using Structure from Motion and BRDF. IEEE JSTARS 2018. Under review. [Google Scholar]
- Presti, D.L.; Pedroni, S.; Crippa, V. Maximum dry density of cohesionless soils by pluviation and by ASTM D 4253-83: A comparative study. Geotech. Test. J. 1992, 15, 180. [Google Scholar]
- Biliouris, D.; Verstraeten, W.W.; Dutré, P.; Van Aardt, J.A.; Muys, B.; Coppin, P. A compact laboratory spectro-goniometer (CLabSpeG) to assess the BRDF of materials. Presentation, calibration and implementation on Fagus sylvatica L. leaves. Sensors 2007, 7, 1846–1870. [Google Scholar] [CrossRef] [PubMed]
- Stoner, E.R.; Baumgardner, M. Characteristic Variations in Reflectance of Surface Soils 1. Soil Sci. Soc. Am. J. 1981, 45, 1161–1165. [Google Scholar] [CrossRef]
- Rossel, R.V.; Behrens, T.; Ben-Dor, E.; Brown, D.; Demattê, J.; Shepherd, K.; Shi, Z.; Stenberg, B.; Stevens, A.; Adamchuk, V.; et al. A global spectral library to characterize the world’s soil. Earth-Sci. Rev. 2016, 155, 198–230. [Google Scholar] [CrossRef] [Green Version]
- Rieu, M.; Sposito, G. Fractal fragmentation, soil porosity, and soil water properties: I. Theory. Soil Sci. Soc. Am. J. 1991, 55, 1231–1238. [Google Scholar] [CrossRef]
- Rieu, M.; Sposito, G. Fractal fragmentation, soil porosity, and soil water properties: II. Applications. Soil Sci. Soc. Am. J. 1991, 55, 1239–1244. [Google Scholar] [CrossRef]
- Goodman, S.J.; Blakeslee, R.J.; Koshak, W.J.; Mach, D.; Bailey, J.; Buechler, D.; Carey, L.; Schultz, C.; Bateman, M.; McCaul, E.; et al. The GOES-R geostationary lightning mapper (GLM). Atmos. Res. 2013, 125, 34–49. [Google Scholar] [CrossRef]
- Bahr, D.B.; Hutton, E.W.; Syvitski, J.P.; Pratson, L.F. Exponential approximations to compacted sediment porosity profiles. Comput. Geosci. 2001, 27, 691–700. [Google Scholar] [CrossRef]
- Bagnold, R.A. The Physics of Blown Sand and Desert Dunes; Courier Corporation: Chelmsford, MA, USA, 1941. [Google Scholar]
- Kok, J.F.; Parteli, E.J.; Michaels, T.I.; Karam, D.B. The physics of wind-blown sand and dust. Rep. Prog. Phys. 2012, 75, 106901. [Google Scholar] [CrossRef] [PubMed]
- Ahlbrandt, T.S. Textural parameters of eolian deposits. In A Study of Global Sand Seas; United States Geological Survey Professional Paper; United States Government Printing Office: Washington, DC, USA, 1979; Volume 1052, pp. 21–52. [Google Scholar]
- Owen, P.R. Saltation of uniform grains in air. J. Fluid Mech. 1964, 20, 225–242. [Google Scholar] [CrossRef]
- Peterson, T.C.; Vose, R.S. An overview of the Global Historical Climatology Network temperature database. Bull. Am. Meteorol. Soc. 1997, 78, 2837–2849. [Google Scholar] [CrossRef]


















| Sample Name | GPS Location | Bulk Density (g/cm) |
|---|---|---|
| BC01-01 | 55′8.25″N, 7′2.42″W | 1.96 |
| BC01-02 | 55′9.47″N, 7′0.06″W | 2.25 |
| BC02-01 | 54′54.77″N, 6′33.03″W | 2.18 |
| BC02-02 | 54′55.35″N, 6′33.91″W | 2.08 |
| BC03-01 | 54′55.07″N, 6′34.76″W | 2.02 |
| BC03-02 | 54′53.98″N, 6′34.26″W | 2.19 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Eon, R.S.; Bachmann, C.M.; Gerace, A.D. Retrieval of Sediment Fill Factor by Inversion of a Modified Hapke Model Applied to Sampled HCRF from Airborne and Satellite Imagery. Remote Sens. 2018, 10, 1758. https://doi.org/10.3390/rs10111758
Eon RS, Bachmann CM, Gerace AD. Retrieval of Sediment Fill Factor by Inversion of a Modified Hapke Model Applied to Sampled HCRF from Airborne and Satellite Imagery. Remote Sensing. 2018; 10(11):1758. https://doi.org/10.3390/rs10111758
Chicago/Turabian StyleEon, Rehman S., Charles M. Bachmann, and Aaron D. Gerace. 2018. "Retrieval of Sediment Fill Factor by Inversion of a Modified Hapke Model Applied to Sampled HCRF from Airborne and Satellite Imagery" Remote Sensing 10, no. 11: 1758. https://doi.org/10.3390/rs10111758
APA StyleEon, R. S., Bachmann, C. M., & Gerace, A. D. (2018). Retrieval of Sediment Fill Factor by Inversion of a Modified Hapke Model Applied to Sampled HCRF from Airborne and Satellite Imagery. Remote Sensing, 10(11), 1758. https://doi.org/10.3390/rs10111758