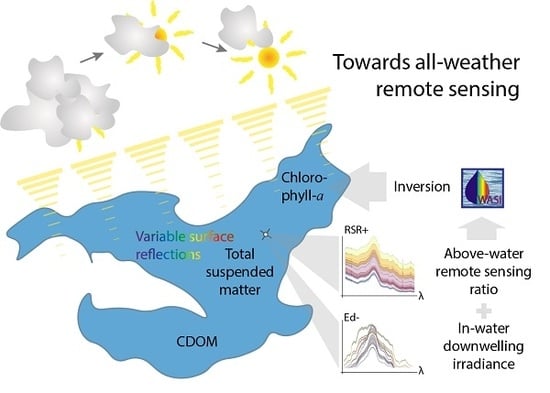
Retrieval of Water Constituents from Hyperspectral In-Situ Measurements under Variable Cloud Cover—A Case Study at Lake Stechlin (Germany)

Abstract

Remote sensing and field spectroscopy of natural waters is typically performed under clear skies, low wind speeds and low solar zenith angles. Such measurements can also be made, in principle, under clouds and mixed skies using airborne or in-situ measurements; however, variable illumination conditions pose a challenge to data analysis. In the present case study, we evaluated the inversion of hyperspectral in-situ measurements for water constituent retrieval acquired under variable cloud cover. First, we studied the retrieval of Chlorophyll-a (Chl-a) concentration and colored dissolved organic matter (CDOM) absorption from in-water irradiance measurements. Then, we evaluated the errors in the retrievals of the concentration of total suspended matter (TSM), Chl-a and the absorption coefficient of CDOM from above-water reflectance measurements due to highly variable reflections at the water surface. In order to approximate cloud reflections, we extended a recent three-component surface reflectance model for cloudless atmospheres by a constant offset and compared different surface reflectance correction procedures. Our findings suggest that in-water irradiance measurements may be used for the analysis of absorbing compounds even under highly variable weather conditions. The extended surface reflectance model proved to contribute to the analysis of above-water reflectance measurements with respect to Chl-a and TSM. Results indicate the potential of this approach for all-weather monitoring.

1. Introduction

Recent advances in sensor technology and progress in algorithm development open new perspectives for inland water remote sensing. Along with an increasing need for water quality monitoring and holistic views on globally distributed inland water ecosystems, remote sensing applications are becoming an important complementary approach to classic monitoring routines [1,2,3,4]. Recent publications cover lake and coastal water observations on a wide spectrum of platforms, ranging from space- and airborne to above-water measurements [4,5,6,7,8]. Major advantages of satellite monitoring are the broad coverage and high repetition rates (e.g., 5 days revisit time for recently launched Sentinel-2 twin satellite mission), which allow for time series studies on a global scale. Automated measurement systems, in turn, which are mounted on jetties, fixed platforms, buoys or ships can provide valuable information about short-term or local changes of water quality parameters and can serve for the calibration and validation of satellite and airborne remote sensing data [9,10,11,12].

While spaceborne optical remote sensing requires mostly clear sky conditions, airborne and in-situ (above- and in-water) measurements can, in principle, be performed on cloudy days as well. A major challenge for this kind of application is that retrieval algorithms need to account for the variability in the illumination conditions. Changes in illumination can lead to intense and highly variable water surface reflections, which depend on several factors such as viewing geometry, sun position, angular distribution of the sky radiance (L_sky), and on the slope distribution of the surface (waves) [13]. Since reflections of direct sunlight (sun glint) and clouds can easily be an order of magnitude higher than the water leaving radiance itself [14,15], their effect needs to be minimized during data acquisition or corrected very accurately during data analysis.

Minimization of sun glint is possible, for instance, when choosing an observation geometry that reduces the probability of specular reflection of the sun disk by accounting for the slope distribution of waves [16], or by combining the usage of a polarizer and an optimized viewing geometry [17]. However, such minimization is not always feasible (e.g., due to a fixed viewing geometry on a satellite/aircraft), nor always desirable, (e.g., increased path length in shallow waters for bottom substrate classification or anisotropy effects for calibration/validation of remote sensing data [18]). With respect to clouds, measurement protocols for reflection minimization do not exist and suitable procedures are difficult to design.

Recently, a physically based spectral model (3C) was published, which enables correction of remote sensing data and field measurements with respect to surface reflectance at clear sky conditions [19]. It does not require accompanying L_sky measurements and builds on a simple model for cloudless maritime atmospheres that separates the downwelling irradiance into three spectrally different components [20]. The 3C model has been successfully applied for sun glint correction in airborne and satellite imagery [21,22], and it has been proven to enable accurate compensation of errors that remain after correction of reflectance with L_sky measurements, even for mixed and overcast sky conditions [15].

In the present case study, we investigated the potential of water constituent retrieval from hyperspectral in-situ measurements acquired under variable cloud cover without additional L_sky measurements.

First, in-water downwelling irradiance measurements were analyzed with a focus on the determination of Chlorophyll-a (Chl-a) concentration and colored dissolved organic matter (CDOM) absorption. Here, the 3C model was applied to handle the so-called wave focusing effect [23,24], i.e., the variability of direct and diffuse components induced by the waves [25]. Since the impact of clouds on downwelling irradiance is spectrally approximately neutral in the visible [26,27], it was simulated by dimming the direct and diffuse components of irradiance. The parameters of the 3C model account for this dimming. Thus, clouds were not treated separately in this part of the analysis.

For above-water measurements, clouds are of particular relevance as they can induce a very large offset in the reflectance. Therefore, in the second part of this study, the impact of reflections at the water surface on the retrieval of Chl-a concentration, CDOM absorption at 440 nm and total suspended matter (TSM) concentration from above-water reflectance measurements was examined. To enable separate modeling of cloud reflections, the 3C model was extended by a constant offset. We examined which of the parameters of the resulting four component (4C) model need to be treated as fit parameters during inversion in order to mimic the surface reflectance. Water constituents were determined by coupling the 4C model with a bio-optical model of the water body [28,29] and fitting the relevant unknown parameters of both models together. Results were compared against data from laboratory analysis of water samples and from a submersible spectrofluorometer.

2. Materials and Methods

2.1. Overview of Measurements and Methodology in This Study

The aim of this study was to evaluate water constituent retrieval from hyperspectral above-water radiance reflectance and in-water irradiance measurements under highly variable illumination conditions. Figure 1 gives an overview of all measurements and derived parameters (first row). They are explained in more detail in the following Section 2.3 and Section 2.4. The second row of Figure 1 summarizes the analysis of in-water irradiance spectra which were recorded at different depths (z) and analyzed in two approaches for the determination of CDOM absorption at 440 nm, and Chl-a concentration (see Section 2.6.1 and Section 3.2). The third row in Figure 1 illustrates the retrieval of CDOM absorption at 440 nm and Chl-a and TSM concentration from above-water radiance reflectance measurements. Here, different surface reflectance correction procedures (A)‒(K) were tested and the best performing approach was selected for water constituent retrieval (see Section 2.6.2 and Section 3.3). The inversion retrieval results were compared to results from water sample analysis. Models applied during the inversion analysis are described in Section 2.5.

2.2. Test Site and Measurement Conditions

During a field campaign on 31 May 2016, an extensive data set of in-situ measurements (above-water and in-water hyperspectral measurements as well as water samples for laboratory analysis) was collected at the deepest point of Lake Stechlin (shortest distance to shore is about 400 m). The lake is located in the federal state of Brandenburg, North-East Germany (53°10′N, 13°02′E) at approximately 60 m above sea level [30]. It is weakly connected to Lake Nehmitz via two channels, which earlier served as in- and outflow channels in a cooling circuit for a nuclear power plant (KKW Rheinsberg—active from 1961 to 1990). Lake Stechlin is surrounded by beech and pine forests and has an area of approximately 4.12 km². It is almost exclusively ground water fed and has a maximum depth of 69.5 m. Lake Stechlin is a hard water lake and has a meso-oligotrophic status. Physical, chemical and biological factors have been intensively studied since the 1960s [31].

Sky conditions were highly variable during the period of hyperspectral measurements (Figure 2): continuous cloud layers of variable thickness covered the sky while the first spectra were recorded. These layers diminished until sun began to break through the clouds. During the subsequent measurements, more direct sunlight fell through gaps between clouds, until conditions right above the test site were mostly sunny (for more details, see Section 3.3).

2.3. Water Constituents and Vertical Profiles

Water samples were taken in parallel to hyperspectral measurements from below the water surface. The spectral light absorption coefficient (360–700 nm, in 2-nm steps) of the sample including dissolved and particulate matter without the contribution of pure water, $a_{CDOM+p}\left(\lambda \right)$, was determined from triplicate measurements with a point-source integrating-cavity absorption meter (PSICAM) [32]. The PSICAM was calibrated before sample measurements using a colored dye solution; temperature effects from pure water absorption were corrected [33]. In order to determine the absorption coefficient of colored dissolved organic matter, $a_{CDOM}$(λ), the sample water was filtered through a 0.2-µm membrane filter (GSWP, Millipore) and measured both in the PSICAM and with a 2-m path length liquid waveguide capillary cell (LWCC; WPI Inc., Sarasota, FL, USA) setup [34]. Spectral absorbance values were converted to absorption coefficients according to Beer’s law. Then, the CDOM spectral slope parameter $S_{CDOM}$ (nm⁻¹) was derived from an exponential fit to the absorption coefficient spectrum in a wavelength range of 360–520 nm (symmetric around 440 nm):

$$a_{CDOM}\left(\lambda \right)=a_{CDOM}\left(440\right)·e^{-S_{CDOM}\left(\lambda -440\right)}.$$

(1)

In addition to absorption, total suspended matter concentration, $C_{TSM}$, was determined in four sets of four filters following the approach of Röttgers et al. [35] by filtering different volumes (0.5, 1, 1.5 and 2 l) of lake water through pre-combusted and weighted GF/F filters (Whatman). After drying the filters at 65 °C (1 set of filters) and 105 °C (3 set of filters), their dry weight was measured and filter weights of the empty filters were subtracted. The final TSM concentration was derived from linear regression of the masses versus the respective volumes.

Beam attenuation was measured using an in-situ spectrophotometer (Wetlabs AC-S), additionally allowing to determine the total scattering coefficient at 650 nm, $b\left(650\right)$. The backscattering coefficient, $b_b\left(650\right)$, was recorded using an in-situ backscatter meter (Wetlabs ECO-VSF). The specific backscattering coefficient of TSM $b_b^{*}\left(650\right)$ was calculated by normalization to the total suspended matter concentration:

$$b_{b,TSM}^{*}=\frac{1}{C_{TSM}}·b_b\left(650\right).$$

(2)

Analogously, the specific scattering coefficient $b_{TSM}^{*}$ was calculated by normalization of $b\left(650\right)$ to the total suspended matter concentration.

For determination of Chl-a concentration, $C_{Chla}$, 1 L of lake water was filtered under low ambient room light onto GF/F filters (Whatman) and stored in liquid nitrogen (in the dark). After transportation to a different laboratory, pigments were extracted from filters (triplicates) in 5 mL of 90% acetone (24 h) and the extract was subsequently analyzed by high performance liquid chromatography (HPLC) [36].

Particulate absorption ($a_p\left(\lambda \right)$) was calculated as the difference of $a_{CDOM+p}\left(\lambda \right)$ and $a_{CDOM}\left(\lambda \right)$ as measured with PSICAM. Due to high phytoplankton biomass in the lake water, this absorption spectrum derived from water sample measurements exhibited spectral features similar to pure phytoplankton culture absorption. Therefore, the spectrum was normalized to the Chl-a concentration in (mg m⁻³):

$$a_{ph}^{*}\left(\lambda \right)=\frac{1}{C_{Chla}}·a_p\left(\lambda \right),$$

(3)

and was added to the spectral library of the inversion software as a specific phytoplankton absorption spectrum $a_{ph}^{*}$(λ) (m² mg⁻¹) for further chlorophyll retrieval.

To determine the phytoplankton community composition, untreated (live) water samples taken from about 0.5 m depth were analyzed in a digital imaging flow-cytometer for particle analysis (FlowCam, Model VS, Fluid Imaging Technologies, Scarborough, ME, USA), immediately after returning to the shore-side lab (within 30 min after sampling). For this purpose, 4× and 10× objectives were used in combination with a 300 µm and 100 µm flow-cell, respectively, with the instrument in automatic imaging mode [37], to account for all particle sizes from 3–300 µm. Image collages were post-analyzed to separate the dominant taxonomic phytoplankton groups and to calculate their biomasses.

Abiotic and biotic parameters were measured at 0.5-m intervals from the surface to the deepest point of the lake. Abiotic variables were measured with a calibrated multi-parameter probe YSI 6600 (YSI Inc., Yellow Springs, OH, USA), that included sensors for temperature (sensor YSI6560), conductivity (YSI6560), pH (YSI6579), and dissolved oxygen concentration (YSI6150). Biotic variables such as phytoplankton biomass were estimated with a submersible spectrofluorometer (FluoroProbe; bbe Moldaenke; Schwentinental, Germany). Here, total Chl-a concentration was calculated as the sum of four algal pigment groups (cyanobacteria, chlorophytes, cryptophytes and “diatoms”, the latter including all brown pigmented groups of diatoms, chrysophytes, haptophytes and dinoflagellates), measured by the FluoroProbe. The total Chl-a concentration served as comparison values for Chl-a concentration retrieval from in-water downwelling irradiance spectra (see Section 3.2 and Section 3.3).

2.4. Hyperspectral Measurements

Downwelling irradiance $E_d\left(\lambda \right)$, under water was recorded with a hyperspectral radiometer (RAMSES ACC-VIS, TriOS GmbH, Rastede, Germany; spectral sampling interval 3.3 nm at 320–950 nm) [38]. Spectra were resampled on a 1 nm spaced grid by cubic interpolation. In order to estimate sensor response, both rectangular- and Gaussian-shaped resampling with varying Full Width Half Maximum (FWHM) was applied to modeled $E_d\left(\lambda \right),$ in order to simulate data retrieved with the RAMSES sensor. Best matches to spectral signatures in measured irradiance spectra were achieved with a Gaussian-shaped resampling of 8 nm FWHM.

The actual depth of the sensor’s light collector was determined with a measuring tape and a step counter. Although the step counter, in principle, allows to measure length quite accurately (~±2 cm at calm conditions), leveling of the counter had to be estimated. Therefore, a systematic uncertainty of the measured depth in the order of 5–10 cm is assumed. In-water hyperspectral measurements were performed at eight different depths within the first 4 m below water surface.

For above-water measurements, a FREEDOM VIS FSV-305 spectrometer (Ibsen Photonics Inc., Farum, Denmark; 0.5 nm spectral sampling interval at 360–830 nm, field-of-view with optic ~4.5°) and a 10% reflectance standard (Labsphere Inc., North Sutton, NH, USA) were used [39,40]. In nine sets of measurements, first upwelling radiance above the reflectance target (30 spectra each), and subsequently upwelling radiance above water (30 spectra each) was measured in nadir geometry. Raw data was converted to radiance after dark current subtraction by applying sensor response and nonlinearity correction as measured in the laboratory. Downwelling irradiance was calculated by multiplying radiance spectra recorded over the reflectance target with a factor of π and considering the spectral calibration factors of the 10% standard. For simplification, the two types of field spectrometric setups are referred to as RAMSES and FREEDOM VIS instruments. In the following, the symbols plus (+) and minus (−) are used as superscripts to distinguish between above- and in-water measurements, respectively.

Radiance reflectance above water (sometimes also referred to as Remote Sensing Ratio ($RSR$) [41]) was calculated from FREEDOM VIS spectra according to:

$$RS{R}^{+}\left(\lambda \right)=\frac{L_u^{+}\left(\lambda \right)}{E_d^{+}\left(\lambda \right)}.$$

(4)

It should be noted that upwelling radiance, L_u, contains both water leaving radiance and sky radiance due to reflection on the lake surface. For each measurement series, the sun zenith angle was calculated using the Python PyEphem library [42].

2.5. Models for Hyperspectral Data Analysis

2.5.1. Downwelling Irradiance above Water

Downwelling irradiance above water, $E_d^{+}\left(\lambda \right)$, was modeled using the model of Gege [25], which builds on the approach of Gregg and Carder and Bird and Riordan [20,25,43] for clear sky conditions [20,25,43]. It distinguishes between the direct component of downwelling irradiance ($E_{dd}$), and two diffuse components arising from Rayleigh scattering at molecules ($E_{dsr}$), and from Mie scattering at aerosols ($E_{dsa}$). The model expresses $E_{dd}$, $E_{dsr}\mathrm{and}{E}_{dsa}$ as products of the extraterrestrial solar irradiance and a number of transmission functions with the scale height of ozone, H_oz, the Ångström exponent of aerosol scattering, α, the turbidity coefficient β (aerosol optical thickness at 550 nm), and the scale height of precipitable water in the atmosphere, WV, as the most relevant parameters that are frequently unknown. Shadowing effects, as might be introduced by clouds or obstacles, are accounted for by scaling each component with a weight which represents the actual intensity relative to clear and unobscured sky:

$$E_d^{+}\left(\lambda \right)=f_{dd}·E_{dd}\left(\lambda \right)+f_{dsr}·E_{dsr}\left(\lambda \right)+f_{dsa}·E_{dsa}\left(\lambda \right).$$

(5)

$f_{dd}$ is the relative intensity of $E_{dd}$, $f_{dsr}$ that of $E_{dsr}$, and $f_{dsa}$ that of $E_{dsa}$. All $f$s are wavelength independent; they are unity for clear and unobscured sky. The $f$s allow all changes of $E_d^{+}\left(\lambda \right)$ to be modeled that are induced by spectrally neutral modifications of $E_{dd}$, $E_{dsr}$ $\mathrm{or}{E}_{dsa}$ by transmission, scattering or reflection at ‘white’ targets such as clouds. During inverse modeling, the $f$s are treated as fit parameters, while the spectra $E_i\left(\lambda \right)$ are modeled using the parameterization of Gregg and Carder [20], and the spectral database of atmospheric components of Gege [44].

2.5.2. Downwelling Irradiance in Water

The downwelling irradiance in water, $E_d^{-}\left(\lambda ,z\right)$, was modeled using the model of Gege [25]. It assumes that the downwelling irradiance just below the water surface (at depth $z$ = 0) can be described by Equation (5) with a common factor $f_{ds}$ for the two diffuse components ($f_{ds}$ = $f_{dsr}$ = $f_{dsa}$) that allows to combine these as $E_{ds}\left(\lambda \right)=E_{dsr}\left(\lambda \right)+E_{dsa}\left(\lambda \right)$. Values for the $f_{dd}$ and $f_{ds}$ parameters are usually highly variable for an undulated water surface [45], and not known in practice. At depth $z$, $E_{dd}\left(\lambda \right)$ is attenuated by exp{$-\left[a\left(\lambda \right)+b_b\left(\lambda \right)\right]·z/cos{{\theta }^{\prime }}_{sun}\}$ and $E_{ds}\left(\lambda \right)$ is attenuated by exp{$-\left[a\left(\lambda \right)+b_b\left(\lambda \right)\right]·z·l_{ds}\}$, with ${{\theta }^{\prime }}_{sun}$ the sun zenith angle in water and $l_{ds}$ = 1.1156 + 0.5504 $·$ (1 − cos${{\theta }^{\prime }}_{sun}$) the average path length of diffuse radiation relative to sensor depth. The absorption and backscattering coefficients were parameterized in this study as follows:

$$a\left(\lambda \right)=a_w\left(\lambda \right)+C_{Chla}·a_{ph}^{*}\left(\lambda \right)+a_{CDOM}\left(440\right)·e^{-S_{CDOM}·\left(\lambda -440\right)},$$

(6)

$$b_b\left(\lambda \right)=b_{b,w}\left(\lambda \right)+C_{TSM}·b_{b,TSM}^{*}\left(\lambda \right).$$

(7)

In these equations, $a_w\left(\lambda \right)$ and $b_{b,w}\left(\lambda \right)$ are the absorption and backscattering coefficients of pure water, respectively. Absorption of phytoplankton is expressed as a product of the Chl-a concentration, $C_{Chla}$, and the specific phytoplankton absorption coefficient, $a_{ph}^{*}$(λ). CDOM absorption is approximated as an exponential function, as usual (see studies by Bricaud et al. and Carder et al. [46,47]). In this description, the slope $S_{CDOM}$ is related to the composition, and the absorption coefficient at 440 nm, $a_{CDOM}\left(440\right)$, is taken as a proxy for the concentration. Backscattering of total suspended matter (including phytoplankton) is treated as a product of TSM concentration, $C_{TSM}$, and a specific backscattering coefficient, $b_{b,TSM}^{*}$(λ). Since $b_{b,TSM}^{*}$(λ) is weakly dependent on wavelength in coastal and inland waters [48,49], and no information about its wavelength dependency was available for Lake Stechlin, a constant value derived from in-situ measurements was used (see Section 3.1).

It was shown by Gege [25] that this separate treatment of direct and diffuse components allows the diffuse attenuation coefficient, $K_d\left(\lambda \right)$, which is an apparent optical property describing the depth change of $E_d^{-}\left(\lambda ,z\right)$, to be replaced with the inherent optical property $\left[a\left(\lambda \right)+b_b\left(\lambda \right)\right]$. The model has been validated against Hydrolight and field measurements. It has been implemented into the public domain software Water Colour Simulator (WASI) [50], which was used for hyperspectral data analysis in this study. In contrast to Hydrolight, WASI can be used for inversion. To the authors’ best knowledge, this is the only model that can handle the high variability of $E_d^{-}\left(\lambda ,z\right)$ measurements induced by wave focusing. Inverse modeling allows the derivation of the sensor depth $z$, the concentration of phytoplankton and the absorption coefficient of CDOM if $f_{dd}$ and $f_{ds}$ are treated as fit parameters together with $z$, $C_{Chla}$ and $a_{CDOM}\left(440\right)$ [44,51].

2.5.3. Reflections at the Water Surface

For clear sky conditions, light reflected at the water surface originates from direct sunlight and diffuse sky light. The spectral radiance of these components can be described well by the three components (3C) $E_{dd}\left(\lambda \right)$, $E_{dsr}\left(\lambda \right)$ and $E_{dsa}\left(\lambda \right)$ of Equation (5). If $g_{dd}$, $g_{dsr}$ and $g_{dsa}$ denote the respective reflection factors, the sky radiance reflected from the water surface towards a sensor can be written similar to Equation (5) as [19]:

$$L_{sky}\left(\lambda \right)=g_{dd}·E_{dd}\left(\lambda \right)+g_{dsr}·E_{dsr}\left(\lambda \right)+g_{dsa}·E_{dsa}\left(\lambda \right).$$

(8)

For the hypothetical case of a uniform sky, a plane water surface and a viewing direction which avoids specular reflection of the sun disk, g_dd = 0 and g_dsr = g_dsa = 1/π = 0.32 sr⁻¹. A changing water surface can cause rapid variation of the $g_i$ while the $E_i\left(\lambda \right)$ remain constant. The resulting variability of the $g_i$ can be accounted for during inverse modeling by treating them as fit parameters, while the spectra $E_i\left(\lambda \right)$ are modeled as described in Section 2.5.1. It was shown that the 3C model is well-suited for correcting field measurements for sun and sky reflections [15].

For overcast sky, the reflected clouds induce an offset to reflectance measurements which is spectrally almost neutral in the visible wavelength range [27]. Reflections at the water surface are thus parameterized by the following four component (4C) surface reflectance model:

$$R_{surf}\left(\lambda \right)=\frac{L_{sky}\left(\lambda \right)}{E_d\left(\lambda \right)}+d_r,$$

(9)

with $d_r$ denoting a spectrally constant cloud offset.

2.5.4. Remote Sensing Reflectance

For measurements above water, the water leaving radiance, $L_w\left(\lambda \right)$, bears all information about the water body. The ratio of water leaving radiance to downwelling irradiance is called remote sensing reflectance, $R_{rs}\left(\lambda \right)$. It is related to subsurface reflectance $r_{rs}^{-}\left(\lambda \right)$ as follows [52,53]:

$$R_{rs}\left(\lambda \right)=\frac{\zeta ·r_{rs}^{-}\left(\lambda \right)}{1-\Gamma ·r_{rs}^{-}\left(\lambda \right)},$$

(10)

where ζ is the water-to-air radiance divergence factor (≈0.52), and the denominator with Γ ≈ 1.6 accounts for the effects of internal reflection from water to air. In our study, the parameters ζ and Γ are parameterized as described by Albert and Gege [54]. $r_{rs}^{-}\left(\lambda \right)$ was calculated using the bio-optical model of Albert [28,29], which has been derived using Hydrolight simulations. In this semi-analytical model, the absorption and backscattering coefficients of the water body are parameterized using Equations (6) and (7). A similar $r_{rs}^{-}\left(\lambda \right)$ model has been developed by Lee et al. [53,55], but Albert’s model additionally accounts for the sun zenith angle and the viewing angle, and it covers a wider range of environmental parameters, including most of the high concentrations of water constituents as observed in inland waters. More details on the applied models and a comparison with the models and parameter ranges of Lee et al. [53,55] can be found in Gege [56].

2.6. Water Constituent Retrieval

2.6.1. Water Constituent Retrieval from In-Water Irradiance

Inverse modeling of downwelling in-water irradiance measurements was realized with the Water Colour Simulator software (WASI) [50]. First, downwelling irradiance measurements above water were fitted using the $E_d^{+}$(λ) model described in Section 2.5.1, in order to derive the atmospheric parameters α, β, H_oz and WV [20,25,43]. These parameters were then kept constant for further in-water irradiance modeling. For water-constituent retrieval, in-water irradiance measurements were analyzed using the $E_d^{-}\left(\lambda ,z\right)$ model described in Section 2.5.2. In the fit procedure, identical start values of fit parameters within each measurement series were selected. As parameters of the bio-optical model, $S_{CDOM}$, $C_{TSM}$, and $b_{b,TSM}^{*}$(λ), (compare Equations (6) and (7)), were kept constant to values derived from laboratory analysis of water samples. Phytoplankton was modeled using $a_{ph}^{*}\left(\lambda \right)$ derived from PSICAM measurements (see Section 2.3). Water temperature, $T$, was set to measured values for each depth.

Two inversion approaches were compared: First, only $C_{Chla}$, $a_{CDOM}\left(440\right)$, $f_{dd}$ and $f_{ds}$ were chosen as fit parameters (start parameters were taken from water samples analysis). In the second run, sensor depth z was added to the set of fit parameters.

2.6.2. Water Constituent Retrieval from above-Water Radiance Reflectance

For inversion of above-water radiance reflectance measurements $RS{R}^{+}\left(\lambda \right)$, a combined model for the contributions from the water body, $R_{rs}\left(\lambda \right)$, and the water surface, $R_{surf}\left(\lambda \right)$, was used:

$$RS{R}^{+}\left(\lambda \right)=R_{rs}\left(\lambda \right)+R_{surf}\left(\lambda \right).$$

(11)

$R_{rs}\left(\lambda \right)$ was calculated as described in Section 2.5.4 based on the bio-optical model of Albert for optically deep water [28,29]. Similar to the analysis of in-water measurements, $b_{b,TSM}^{*}$ and $S_{CDOM}$ were treated as constant and set to values derived from in-situ measurements and laboratory analysis. Also, the $a_{ph}^{*}\left(\lambda \right)$ spectrum as derived from PSICAM measurements was used (see Section 2.3). $C_{Chla}$, $C_{TSM}$ and $a_{CDOM}\left(440\right)$ were treated as fit parameters during inverse modeling.

The light reflected at the water surface is the most critical component for measurements under variable cloud cover. Its reflectance $R_{surf}\left(\lambda \right)$ was parameterized using the 4C model (Equation (9)). Different combinations of the clear sky parameters g_dd, g_dsr and g_dsa and the cloud offset $d_r$ were tested to minimize the number of fit parameters for reflections at the water surface.

After retrieval of atmospheric parameters from the respective $E_d^{+}\left(\lambda \right)$-spectra (analogue to Section 2.6.1), $RS{R}^{+}\left(\lambda \right)$ was fitted to the measured radiance reflectance spectra using a least-squares-fit. In order to identify the best-suited set of fit parameters, inversion was performed in various approaches representing different sets of variables for modeling the surface reflectance $R_{surf}\left(\lambda \right)$ (see Section 3.3). Start parameters per measurement series were determined by pre-fitting the first spectrum of the corresponding series. The average residuum of the least-squares-fit was normalized to the maximum reflectance of the series and taken as an indicator for spectral matching of the respective approach. Finally, the best approach in terms of smallest number of fit parameters, spectral matching and lowest variance in retrieved water constituents was determined, and retrieved water constituents were compared against results from water sample analysis.

3. Results and Discussion

3.1. Water Constituents and Phytoplankton Community

Results from water analytics served as a comparison to values retrieved from hyperspectral data and are summarized in

Table 1. Results from water sample and in-situ probe data analysis.

SCDOM (nm−1)	aCDOM(440) (m−1)	CChla (µg L−1)	CTSM (mg L−1)	bb,TSM (m−1)	bTSM (m−1)
0.017 ± 0.002 1	0.21 ± 0.01 1	14.4 ± 0.5 3	2.05 ± 0.17	0.026 ± 0.01	2.14 ± 0.09
0.017 ± 0.002 2	0.25 ± 0.01 2	12.4 ± 1.0 4

¹ PSICAM; ² LWCC; ³ HPLC; ⁴ bbe-fluoroprobe (at 0.2 m).

. Exponential fits to spectral absorption of CDOM, measured both with the PSICAM and LWCC setup, resulted in slope values $S_{CDOM}$ of 0.017 ± 0.002 nm⁻¹. The corresponding absorption values (at 440 nm) are 0.21 ± 0.01 m⁻¹ for PSICAM and 0.25 ± 0.01 m⁻¹ for LWCC measurements. CDOM slope results are comparable to values reported for lakes in the literature, though retrieved over different wavelength ranges [57,58]. For total suspended matter (TSM), the largest volume was omitted as measurements and results indicated an underestimation of the masses for these filters. Gravimetrically derived values were averaged, resulting in a concentration of 2.05 ± 0.17 mg L⁻¹. Chl-a concentration from HPLC analysis was 14.4 ± 0.5 µg L⁻¹ which is a rather high concentration for Lake Stechlin in the upper layer, where typical values range between 0.7–9.5 (mean: 2.3) µg L⁻¹ [59].

Specific backscattering and specific scattering coefficients were derived from in-situ data of a spectrophotometer and a backscattering meter by normalization to the TSM concentration. The resulting coefficients are $b_{b,TSM}^{*}$ = 0.0128 m² g⁻¹ and $b_{TSM}^{*}$ = 1.04 m² g⁻¹.

Vertical temperature and oxygen saturation profiles, as measured with the YSI probe, revealed a stratification of the water body with a thermocline (steepest temperature gradient) between 4.5 and 4.6 m. Temperature in the upper mixed layer of the water column (epilimnion), where in-water irradiance spectra were recorded, ranged between 18 and 19 °C. Analysis of bbe-fluoroprobe data showed that the total Chl-a concentration, as measured in-situ, was 12.4 ± 1.0 µg L⁻¹ below the surface with similar values in the upper mixed layer (0–5 m).

According to the FlowCam analysis, the surface water was dominated (in terms of abundance) by cyanobacteria followed by chrysophytes, which showed up as “diatoms” in the bbe-fluoroprobe (because the fluoroprobe cannot distinguish the brown-pigmented algal groups such as diatoms, chrysophytes, haptophytes, and dinoflagellates). Retrieved abundances and cell sizes of the phytoplankton groups were converted to carbon-biomass using the equations presented in Menden-Deuer et al. [60]. This post-analysis of the image collages from FlowCam measurements revealed that the water samples (in terms of biomass) were dominated by two large phytoplankton taxa: filamentous cyanobacteria mainly represented by Dolichospermum zinserlingii (Kossinskaja) Wacklin, Hoffmann and Komárek, and by colonial chrysophytes mainly represented by Dinobryon sociale (Ehrenberg) Ehrenberg. These findings agree with spectral signatures as observed in the $a_{ph}^{*}\left(\lambda \right)$ spectrum which, in addition to signatures of Chl-a, showed a maximum at around 630 nm which indicates the presence of phycobilin-containing phytoplankton such as cyanobacteria.

3.2. Water Constituent Retrieval from Downwelling Irradiance Spectra under Water

In order to test the applicability of the clear sky inversion model, above-water downwelling irradiance was modeled, as explained in Section 2.6.1. When fitting the irradiance model to $E_d^{+}$ measurements, a strong deviation in the 700–900 nm range was observed. The upwards shift of the red and near infrared parts of the measured spectrum compared to the modeled spectrum occurred in a wavelength range where vegetation has a high reflectance. This increase was observed with both the FREEDOM VIS and the RAMSES instrument. It may indicate adjacency effects caused by surrounding vegetation [61]. To minimize its impact on modeling, the fit range for deriving atmospheric parameters was limited to 350–700 nm, which was also kept for in-water hyperspectral data analysis.

Atmospheric parameters that described illumination conditions best (lowest residuum of the least-square fit), were averaged over the 30 spectra, which resulted in α = 3.00, β = 0.26, H_oz = 0.49 cm⁻¹, WV = 3.35 cm⁻¹. Some of these parameters may not represent real physical values (e.g., typical values for α—albeit in different environments—range between 0 and 2 [62,63]). Thus, this step should be seen as a pragmatic approach to constrain the variability of downwelling irradiance that helps to reduce the number of free parameters in the subsequent step. In that step, which is fitting of underwater irradiance spectra ($E_d^{-}$), these parameters were kept constant. In addition, $C_{TSM}$ was set to the measured mean value of 2.05 mg L⁻¹ since pre-studies demonstrated a low sensitivity of the irradiance model to TSM. Also, $S_{CDOM}$, $b_{b,TSM}^{*}$ and $b_{TSM}^{*}$ were kept fixed to measured values (0.017 nm⁻¹, 0.0128 m² g⁻¹ and 1.04 m² g⁻¹, respectively). Then, two different approaches were chosen: in the first approach, the sensor depth z was set to the actual measured depth, while in the second approach z was added to the set of fit parameters and varied during modeling. For each depth, a series of 30 individual spectra was inverted.

In the case of fixed sensor depth z, Chl-a concentration below the surface deviated from water sample analysis by about 35%, and from in-situ spectrofluoreometric measurements by about 56% in the first meter of water depth, but became comparable to results from water analytics at greater depths (see Figure 3a). This is in accordance with previous studies which showed that, for accurate Chl-a concentration retrieval, a layer of water above the sensor of at least 1 m (depending on overall water constituent concentration ranges) was required [44,51]. $a_{CDOM}$(440), compared to results from water analytics, showed a deviation of about 57% from PSICAM and 32% from LWCC measurements. Error bars of the WASI fit-results represent the variability within the 30 spectra series.

In the case of a varied sensor depth z, an improved agreement between retrieved concentration from downwelling irradiance measurements below the water surface and results from water sample analysis was achieved (Figure 3b). Chl-a concentration at 40 cm water depth deviated from water sample analysis by only 5% and from in-situ spectrofluorometric measurements by 22%. CDOM absorption at 440 nm differed from PSICAM measurements by about 19% and matched the value derived from LWCC measurements. The respective values for z showed a linear correlation with measured depths, but with a deviation from the expected 1:1 relationship. The regression line (not shown) exhibited a slope of 0.88 and an offset of 0.26 m, suggesting that the sensor depth was systematically overestimated by the fit. One possible interpretation is that, under the cloudy weather conditions, more light may have entered the water body at a flat angle compared to clear sky conditions. This would result in longer absorption path lengths at a given depth. The inverse modeling may compensate this by an increased sensor depth.

3.3. Water Constituent Retrieval from Radiance Reflectance Spectra above Water

As described in Section 2.2, the fraction of cloud cover, cloud thickness and the resulting illumination conditions were highly variable during the period of hyperspectral measurements. The irradiance spectra measured with the FREEDOM VIS spectrometer reflect this variability as can be seen in Figure 4. The plot on the left-hand side (Figure 4a) compares the spectral irradiances when the sun is obscured by clouds (M3) and when the sun is visible (M8). The changes in the magnitude of irradiance during all measurement series are illustrated in Figure 4b. The magnitude varied roughly by a factor of 3. Note that in measurement M7, instrument saturation effects were observed for a number of spectra. Therefore, 25 spectra had to be removed, which led to a reduced number for the average $E_d^{+}$(λ) spectrum. Figure 4c depicts the relative standard deviation of irradiance spectra for all measurements (grey line) and for measurements where the sun was mostly obscured by thick clouds (M1–M3 black line). From a comparison of Figure 4b,c it can be concluded that the clouds covering the sun in measurements M1–M3 did mainly affect the magnitude of irradiance but its spectral shape remained approximately constant in the visible wavelength range.

Radiance reflectance above water measured with the FREEDOM VIS instrument was highly variable as shown in Figure 5a. Within and between the measurement series (M1–M9) an offset-like shift in the intensities was observed. For inversion, the wavelength range was set to 360–830 nm, in order to cover the wavelength region above 700 nm that is often used to correct for sun glint [14].

Fitting the individual radiance reflectance spectra without surface reflection effects (approach (K)), or a model that only varies direct and diffuse components of downwelling spectral irradiance (approach (A)) [44], were both unsuccessful (

Table 2. Spectral matching of fitted and measured radiance reflectance (series M1–M9) for different inversion approaches (A–J), where (+) and (−) indicate the quality of the spectral matching between fit and measurement curves. The (+) stands for least-squares-fit residual (normalized to max. reflectance) smaller than the average residuum by at least a factor of 2.

Fixed Surface Parameters	Varied Parameters		M1	M2	M3	M4	M5	M6	M7	M8	M9
gdsr, gdsa = 0.32 gdd = 0.02 | dr = 0	fdd, fds	A	−	−	−	+	+	−	−	+	+
fdd, fds = 1 | gdsa, gdsr, gdd = 0	dr	B	+	+	+	−	−	+	−	−	+
fdd, fds = 1 | gdsa, gdsr = 0 |dr = 0	gdd	C	−	−	−	−	−	−	−	−	−
fdd, fds = 1 | gdsa, gdd = 0 |dr = 0	gdsr	D	−	−	−	−	−	−	−	−	−
fdd, fds = 1 | gdsr, gdd = 0 |dr = 0	gdsa	E	−	−	−	−	−	−	−	+	−
fdd, fds = 1 | gdsa = 0	gdsr, gdd	F	+	+	+	+	+	+	+	+	+
fdd, fds = 1 | gdsa = 0	gdsr, dr	G	+	+	+	+	+	+	+	+	+
fdd, fds = 1 | gdsa = 0	gdd, gdsr, dr	H	+	+	+	+	+	+	+	+	+
fdd, fds = 1 | dr = 0	gdd, gdsa, gdsr	I	+	+	+	+	+	+	+	+	+
fdd, fds = 1	gdd, gdsa, gdsr, dr	J	+	+	+	+	+	+	+	+	+
No surface reflections	-	K	−	−	−	−	−	−	−	−	−

): Either the batch processing of the measurement series in WASI failed (in terms of spectral matching), or in cases where spectral matching was achieved, the inversion led to vanishing values for CDOM absorption. Therefore, variable surface reflectance components as described in Section 2.6.2 were introduced in subsequent inversion runs. Here, additional glint components were successively added to the set of fit parameters in order to determine best spectral matching with a minimal number of fit parameters. Each set of spectra (M1–M9) was fitted with the resulting approaches (B–J), respectively. Table 2 summarizes all approaches and their choice of free and fixed surface reflectance parameters during determination of Chl-a, TSM concentration and $a_{CDOM}$(440). It also gives an overview of the spectral matching that was achieved.

Best spectral matching with just one variable surface reflectance component was achieved with approach (B). However, this approach induced a high variability in the Chl-a retrieval and an unrealistically high correlation between retrieved Chl-a and TSM values (see

Table 3. Comparison of the variability (standard deviation σ) and the correlation (Spearman’s rank correlation coefficient r) of water constituents retrieved from 260 above-water measurements for the surface reflectance correction approaches (B and F–J). These were the approaches that showed a reasonable spectral matching during inversion (compare Table 2).

	B	F	G	H	I	J
# surface parameters	1	2	2	3	3	4
Average residua	1.57 × 10−5	1.06 × 10−5	9.56 × 10−6	9.47 × 10−6	8.78 × 10−6	9.28 × 10−6
σ ($C_{Chla}$ (µg L−1))	1.21	0.60	0.66	0.79	1.10	0.82
σ ($C_{TSM}$ (mg L−1))	0.23	0.21	0.20	0.21	0.21	0.19
$a_{CDOM}\left(440\right)$ (m−1)	0.00 ± 0.00	0.11 ± 0.03	0.09 ± 0.04	0.09 ± 0.03	0.08 ± 0.03	0.10 ± 0.05
r ($C_{Chla}$|$C_{TSM}$)	0.77	0.22	0.44	0.53	0.55	0.34
r ($C_{Chla}$|$C_{CDOM}\left(440\right)$)	−0.02	−0.36	−0.12	−0.17	−0.55	−0.44
r ($C_{CDOM}$|$C_{TSM}$)	0.55	0.61	0.47	0.41	0.10	−0.42
r ($C_{Chla}$|surf)°	0.57 (dr)	−0.29 (gdd)	−0.50 (gdsr)	−0.52 (gdsr)	0.67 (gdsa)	−0.46 (gdsr)
r ($C_{TSM}$|surf)°	0.55 (dr)	0.71 (gdsr)	0.65 (dr)	0.61 (dr)	0.66 (gdsa)	0.44 (gdsa)
r ($a_{CDOM}\left(440\right)$|surf)°	0.67 (dr)	0.84 (gdsr)	0.69 (dr)	0.64 (dr)	0.51 (gdsr)	0.79 (gdsr)

^° highest correlation of retrieved water constituent parameter with a surface parameters (which).

). Furthermore, it resulted in vanishing CDOM absorption (similar to approach (A)), which is inconsistent with the in-situ measurements. The Chl-a and TSM correlation decreased with the addition of more surface reflectance parameters (see Table 3). Approaches (F–J) all resulted in good spectral agreement between fit and measurement curves for all series of measurements. Figure 5b shows an example of such a fit result for an individual measurements series (M4) that was fitted with approach (G). The lowest variability of retrieved inversion parameters was achieved with approach (F), but here a very strong correlation of $a_{CDOM}\left(440\right)$ and g_dsr was observed (r = 0.84). Correlation between these parameters can be understood since both CDOM absorption and Rayleigh scattering show a continuously decaying spectral behavior towards larger wavelengths. As a compromise in the number of free fit parameters, the variability of the retrieved water constituents and the correlation with other water constituents and surface parameters, approach (G) proved to be the most successful in correcting surface reflectance in the present case study.

Water constituents retrieved with approach (G) were compared against results from water sample analysis and in-situ probe data (see

Table 4. Water constituents as retrieved from above-water reflectance under variable cloud cover with correction of cloud reflection and surface reflection originating from Rayleigh scattered light (Errors represent the variability of the fit results)—Results from water sample analysis and in-situ probe data.

	CChla (µg L−1)	CTSM (mg L−1)	aCDOM(440) (m−1)
Reflectance inversion approach (G)	9.1 ± 0.7	1.4 ± 0.2	0.09 ± 0.04
Water sample	14.4 ± 0.5	2.1 ± 0.1	0.21/0.25 ± 0.01/0.01 *
Fluorescence probe	12.4 ± 1.0	-	-

* PSICAM/LWCC.

). Chl-a concentration retrieved from above-water hyperspectral measurements differed by 37% from results from water sample analysis and by 27% from subsurface fluoroprobe data. The deviation of TSM from water sample analysis was about 33%. $a_{CDOM}\left(440\right)$ retrieved with inversion turned out to be roughly 60% (57% and 62%, respectively) smaller than results from LWCC and PSICAM measurements. The spurious correlation of retrieved water constituents with surface reflectance parameters needs to be further investigated in future studies. An extended measurement wavelength range towards the infrared, where water absorption increases, may help to further disentangle, e.g., the effect of TSM and the cloud parameter d_r on the reflectance signal.

4. Conclusions

During a field campaign at Lake Stechlin in May 2016, a set of hyperspectral measurements under variable sky conditions was collected both in and above water. These spectra were complemented by a comprehensive set of water sample and in-situ probe data. The aim of this study was to evaluate the potential of water constituent retrieval from hyperspectral in-situ measurements acquired under variable cloud cover.

First, Chl-a concentration and $a_{CDOM}^{}$(440) were retrieved from in-water downwelling irradiance spectra at different depths using a clear sky model. Clouds were simulated by a dimming of the fraction of direct and diffuse irradiance as parameters of the 3C model. When varying the sensor depth along with targeted water constituents, a reasonable agreement between retrieved water constituent concentrations and the results from water sample analysis was achieved. CDOM absorption at 440 nm differed by about 19% from PSICAM measurements and coincided with LWCC measurements. The simultaneously derived phytoplankton concentration showed a deviation of 22% from in-situ probe data and a 5% deviation from HPLC measurements. The sensitivity of the $E_d^{-}$-model to the sensor depth z and the improved retrieval results suggest a fitting of sensor depth for water constituent retrieval from in-water irradiance measurements.

In addition to in-water downwelling irradiance measurements, above-water radiance reflectance measurements were analyzed. In order to account for cloud effects, the 3C model was extended by a variable offset $d_r$ resulting in the 4C spectral model for the description of surface reflectance. A common goal in analytical inversion modeling is to reduce parameters in order to minimize spectral ambiguity. Therefore, the introduction of additional fit parameters should be handled with caution. In the present study, the best set of parameters for describing surface reflectance was determined in eleven test configurations. The best results in terms of minimum number of fit parameters, lowest correlation of retrieved water constituents and surface reflectance components were achieved when treating d_r and g_dsr as fit parameters. The retrieved Chl-a concentration differed from HPLC results by about 37% and from subsurface active probe data by 27%. TSM retrieved from hyperspectral measurements deviated from gravimetrically determined values by 33%. The most critical parameter was $a_{CDOM}^{}$(440), which correlated with g_dsr and the offset d_r. Derived CDOM absorption values showed a deviation of 57% from LWCC and 62% from PSICAM measurements. Future studies should address the disentanglement of spectral surface reflection signatures from CDOM as well as from TSM signals.

The study has shown that a number of water constituents can be derived from in-water irradiance and above-water radiance reflectance measurements that were recorded under variable cloud cover. To the authors’ knowledge, in-water hyperspectral irradiance measurements under varying cloud cover are rarely analyzed. The present study suggests that, even under mixed skies, in-water irradiance data may help to retrieve information on in-water substances with respect to absorbing compounds while above-water measurements allow for additional insight into the scattering compounds. Further studies are required to validate the extended 4C surface reflectance model but present results indicate its benefit for surface reflection corrections as required in all-weather remote sensing.

Lakes are very dynamic systems. They are subject to biogeochemical processes and influenced by hydrology, weather conditions and human activities such as agriculture in the catchment area and recreational use. In order to capture and to better understand these dynamics, it is crucial to minimize observation gaps. Abandoning the restriction to clear sky conditions would represent a big step forward towards regular monitoring schemes and open the door to more continuous time series of remote sensing data, e.g., from airplanes, unmanned aerial vehicles or ground-based measurements. This study demonstrates the potential of hyperspectral in-situ monitoring under weather conditions that usually constrict remote sensing.