Accuracy Assessment Measures for Object Extraction from Remote Sensing Images

Abstract

Object extraction from remote sensing images is critical for a wide range of applications, and object-oriented accuracy assessment plays a vital role in guaranteeing its quality. To evaluate object extraction accuracy, this paper presents several novel accuracy measures that differ from the norm. First, area-based and object number-based accuracy assessment measures are given based on a confusion matrix. Second, different accuracy assessment measures are provided by combining the similarities of multiple features. Third, to improve the reliability of the object extraction accuracy assessment results, two accuracy assessment measures based on object detail differences are designed. In contrast to existing measures, the presented method synergizes the feature similarity and distance difference, which considerably improves the reliability of object extraction evaluation. Encouraging results on two QuickBird images indicate the potential for further use of the presented algorithm.

1. Introduction

High spatial resolution satellite images are easily available thanks to advancements in modern sensor technology and have led to many applications in various fields, such as agriculture, forestry, and environmental protection [1,2,3]. Compared to medium/low resolution satellite images, high resolution satellite images contain richer information and clearer boundaries, making them attractive for object extraction [4,5,6]. The concept of the object, a group of pixels that share similar properties, was originally proposed in the 1970s [7], triggering a considerable amount of research in object-based image analysis (OBIA). Since its introduction, researchers have wondered how they may assess the results of OBIA.

Noise is inherent in satellite images, and thus, the accuracy of object extraction needs to be examined. This issue has received considerable critical attention [8,9,10,11,12,13,14,15,16,17]. Examples include the error matrix and confusion matrix, which are two typical methods for accuracy assessment. Despite their popularity, these methods ignore object features, making them unsuitable for OBIA accuracy evaluation. A direct solution [18] is to compute error and confusion matrixes on each object rather than at the pixel level. Although this simple solution can amend the shortage of pixel-level error and confusion matrixes to a certain extent, it suffers from the issue of missing the object detail, leading to unreliable evaluation results. To enhance the reliability of this accuracy evaluation, a series of per-object accuracy assessment measures based on object features have been designed [8,19]. Among them, the similarity between evaluation and reference objects (e.g., area, size, shape, and location [19,20,21,22,23,24]) is commonly used. As the similarity measure can judge the correctness of extracted objects, it is possible to obtain numbers of correct, wrong, and missing objects for accuracy evaluation. Statistical values of object similarity (e.g., the weighted average value) are also commonly used measures to directly assess object extraction accuracy [8]. This method exploits the degree of overlap and position difference between evaluation and reference objects for evaluating object extraction accuracy [19,25,26,27,28]. Although these methods have resulted in significant improvements compared to pixel-wise accuracy measures, the effects of geometric information and difference in detail have not been comprehensively examined. Meanwhile, most existing evaluation methods were designed based on geometrical errors associated with objects. The influence of thematic error on object extraction accuracy evaluation, however, lacks a systematic understanding [29,30]. Thus, there is still significant room to improve the generalization ability of existing object-level accuracy measures.

This study investigates the use of four designed accuracy measures for object extraction evaluation. The proposed method systematically studies the influence of object characteristics on extraction accuracy, the aim being to present reliable accuracy measures for object extraction. The remainder of this paper is organized as follows. Section 2 introduces the methodology. The experimental results and discussion are given in Section 3 and Section 4, respectively. Finally, Section 5 concludes the paper.

2. Methodology

This study supposes that remote sensing images have been pre-processed, and have undergone radiometric calibration and geometric correction. The objects are extracted from pre-processed images, and some of the objects are selected as evaluation samples. A unique reference object is matched for each evaluation object. The accuracy evaluation of object extraction is based on object matching.

2.1. Object Matching

Object extraction accuracy is evaluated by comparing the difference between the evaluated object and its reference data, and thus it is fundamental to match the reference and evaluated objects. To this end, this paper matches objects using the maximum overlap area algorithm due to its computation efficiency. The central idea of the maximum overlap area method is to compute the coincidence degree $O_{ij}$ between two objects.

$$O_{ij}=\frac{1}{2}\left(\frac{A_{\mathrm{C},i}\cap A_{\mathrm{R},j}}{A_{\mathrm{C},i}}+\frac{A_{\mathrm{C},i}\cap A_{\mathrm{R},j}}{A_{\mathrm{R},j}}\right)$$

(1)

where $A_{\mathrm{C},i}$ denotes the area of the ith evaluated object, $A_{\mathrm{R},j}$ is the area of the jth reference object, and $A_{\mathrm{C},i}\cap A_{\mathrm{R},j}$ represents the intersection area. For an evaluated object and candidate reference objects, each coincidence degree will be computed. Two objects will be judged as being a matching pair if their coincidence degree is a maximum amongst all pairs.

2.2. Area-Based Accuracy Measures

Three area-based accuracy measures (i.e., correctness, completeness, and quality) are designed for OBIA evaluation. The purpose of area-based accuracy measures is to obtain stable accuracy measurements.

Correctness $P_{\mathrm{AC}}$ is defined as the ratio of correctly extracted area and the whole extracted area.

$$P_{\mathrm{AC}}=\frac{A_{\mathrm{C}}}{A_{\mathrm{DC}}}$$

(2)

where $A_{\mathrm{DC}}$ is the area of the extracted object, and $A_{\mathrm{C}}$ is the correct part of $A_{\mathrm{DC}}$. The range of correctness is from 0 to 1. If all the evaluated objects have their own fully corresponding reference objects, then $P_{\mathrm{AC}}=1$. If there is no evaluated object from the same thematic class overlapping the reference object, then $P_{\mathrm{AC}}=0$.

The ratio of correctly extracted area $A_{\mathrm{C}}$ to the reference area $A_{\mathrm{RC}}$ is called the completeness $P_{\mathrm{AR}}$.

$$P_{\mathrm{AR}}=\frac{A_{\mathrm{C}}}{A_{\mathrm{RC}}}$$

(3)

The range of completeness is 0 to 1. If all reference objects have their own fully corresponding evaluated objects, then $P_{\mathrm{AR}}=1$. If there is no reference object from the same thematic class overlapping the evaluated object, then $P_{\mathrm{AR}}=0$.

Equations (2) and (3) show an interaction between correctness and completeness. For instance, a large $A_{\mathrm{DC}}$ leads to a small correctness value, while a small $A_{\mathrm{RC}}$ results in a large completeness value. To amend this issue, the quality $P_{\mathrm{AL}}$ is designed to balance correctness and completeness.

$$P_{\mathrm{AL}}=\frac{A_{\mathrm{C}}}{A_{\mathrm{DC}}+A_{\mathrm{RC}}-A_{\mathrm{C}}}$$

(4)

The range of quality is 0 to 1. If the extraction results are exactly the same as the reference data, then $P_{\mathrm{AL}}=1$. If no thematic class evaluated object overlaps with the reference object, then $P_{\mathrm{AL}}=0$.

Figure 1 presents two cases to illustrate the advantage of area-based accuracy measures compared to the confusion matrix. The accuracy values of two cases computed by the confusion matrix will be significantly different, as the confusion matrix depends on total pixel number. In contrast, the evaluation results for two cases using area-based accuracy measures are equivalent, because the latter measurements rely only on the evaluation and reference objects and are independent of the total pixel number.

2.3. Number-Based Accuracy Measures

Three accuracy measures (i.e., correct, false, and missing rates), relying on counting the number of objects with different properties, are presented for testing OBIA performance. Specifically, the correct rate $P_{\mathrm{C}}$, the false rate $P_{\mathrm{F}}$, and the missing rate $P_{\mathrm{M}}$ are defined as

$$P_{\mathrm{C}}=\frac{N_{\mathrm{C}}}{N_{\mathrm{C}}+N_{\mathrm{F}}},0\le P_{\mathrm{C}}\le 1$$

(5)

$$P_{\mathrm{F}}=\frac{N_{\mathrm{F}}}{N_{\mathrm{C}}+N_{\mathrm{F}}},0\le P_F\le 1$$

(6)

$$P_{\mathrm{M}}=\frac{N_{\mathrm{M}}}{N_{\mathrm{C}}+N_{\mathrm{M}}},0\le P_M\le 1$$

(7)

where $N_{\mathrm{C}}$, $N_{\mathrm{F}}$, and $N_{\mathrm{M}}$ represent the number of correct, false, and missed extracted objects, respectively. If all evaluated objects are correct, then $P_{\mathrm{C}}=1$ and $P_{\mathrm{F}}=0$. If all evaluated objects are incorrect, then $P_{\mathrm{C}}=0$. If there is no false evaluated object, then $P_{\mathrm{F}}=1$. If all reference objects have their own correct evaluated objects, then $P_{\mathrm{M}}=0$. If no reference object corresponds correctly to the evaluated object, then $P_{\mathrm{M}}=1$.

The purpose of Equations (5)–(7) is to examine if the object is extracted correctly or falsely. To this end, if the proportion of correct pixels to total pixels for an object is larger than a given threshold, it is correctly extracted; otherwise, it is considered to be wrongly extracted.

2.4. Feature Similarity-Based Accuracy Measures

The difference between object-based and pixel-based accuracy measures is the assessment unit. Compared to the pixel, the object consists of many similar pixels, and thus has more features. The object number-based accuracy measures consider feature difference, but omit the feature detail difference and degree of difference between evaluated and reference objects. As shown in Figure 2a, if the area coincidence rate was used as a criterion to judge similarity, two evaluated objects would be judged correctly. However, two evaluated objects would be judged incorrectly, if the maximum deviation distance was used as the distinguishing criterion. Thus, the correctly extracted object number cannot fully reflect the difference between two evaluated objects that have large geometrical differences. The area-based measures can reflect differences between objects, but neglect object features. Although object extraction results may have the same correct, false, and missing rates, different object features derived from satellite images can generate different object qualities. Figure 2b shows that the overlap areas between two evaluated objects and reference objects are the same, but their locations and geometrical characteristics differ. This indicates that using object number or object area independently cannot assess object extraction accurately. This issue can be solved to a certain extent by considering more object features.

Besides object number and object area, object geometric features can also reflect object difference, and thus can be used in complement to measure object extraction accuracy [31]. There are various geometric measures, and this paper selects typical measurements (e.g., area, perimeter, and barycenter) to design accuracy measures for OBIA.

The size difference reflects the basic similarity between two objects. Based on this observation, an object-based accuracy assessment method using size and size similarity $S_{\mathrm{M}}$ is defined as

$$S_{\mathrm{M}}=\frac{\min \left(Siz{e}_{\mathrm{C}},Siz{e}_{\mathrm{R}}\right)}{\max \left(Siz{e}_{\mathrm{C}},Siz{e}_{\mathrm{R}}\right)}$$

(8)

where $Siz{e}_{\mathrm{C}}$ denotes the size of the evaluated object and $Siz{e}_{\mathrm{R}}$ denotes the size of the reference object. Standard geometric features, such as area, perimeter, and outer radius, can be used as assessment indices. The range of size similarity is 0 to 1. If all evaluated objects have the same size as that of the reference object, then $S_{\mathrm{M}}=1$. If no evaluated object has the same size as that of the reference object, then $S_{\mathrm{M}}=0$.

Equation (8) ignores feature details of the object that may lead to inaccurate evaluation results. To tackle this issue, an improved size similarity $S_{\mathrm{F}}$ is presented.

$$S_{\mathrm{F}}=1-\frac{\left|f_{\mathrm{C}}-f_{\mathrm{R}}\right|}{\min \left(f_{\mathrm{C}},f_{\mathrm{R}}\right)}$$

(9)

where $f_{\mathrm{C}}$ is the feature value of the evaluated object, $f_{\mathrm{R}}$ is the feature value of the reference object, and $\left|f_{\mathrm{C}}-f_{\mathrm{R}}\right|$ is the feature difference between evaluated and reference objects. The features used in Equation (9) include area, perimeter, and diameter. The range of improved size similarity is 0 to 1. If all evaluated objects have the same size as that of the reference object, then $S_{\mathrm{F}}=1$. When the ratio between $f_{\mathrm{C}}$ and $f_{\mathrm{R}}$ exceeds 2 or is less than 0.5, then $S_{\mathrm{F}}$ is set to 0.

Equations (8) and (9) are relatively easy to implement, making them suitable for obtaining assessment results in near-real time. However, these two measures completely ignore the location difference that increases errors in the assessment results. To improve the measures in Equations (8) and (9), Tversky’s feature contrast model [32], based on the feature similarity description, was proposed. This model measures $S_{\mathrm{O}}$, the similarity of two objects, using the following equation:

$$S_{\mathrm{O}}=\frac{f\left(C\cap R\right)}{f\left(C\cap R\right)+\alpha f\left(C-R\right)+\beta f\left(R-C\right)}$$

(10)

where $f\left(C\cap R\right)$ are common features of the evaluated object C and its reference object R, $f\left(C-R\right)$ denotes features that belong to the evaluated object C but not reference object R, and $f\left(R-C\right)$ stands for features that belong to the reference object R but not the evaluated object C, and $\alpha$ and $\beta$ are weights for $f\left(C-R\right)$ and $f\left(R-C\right)$, respectively.

Equation (10) can measure the similarity of objects at the class or individual scale. Features in Equation (10) should be selected carefully, as some features (e.g., shape complexity, sphericity, and circularity), are challenging to describe using $f\left(C-R\right)$ and $f\left(R-C\right)$. To improve the generalization of the Tversky’s feature contrast model, this paper defines an improved matching similarity as follows:

$$S_{\mathrm{O}}=\frac{f_{\mathrm{A}}\left(C\cap R\right)}{f_{\mathrm{A}}\left(C\cap R\right)+\alpha f_{\mathrm{A}}\left(C-R\right)+\beta f_{\mathrm{A}}\left(R-C\right)}$$

(11)

where $f_{\mathrm{A}}\left(C\cap R\right)$ represents features of the intersection area of C and R, $f_{\mathrm{A}}\left(C-R\right)$ denotes features of the area of R to erase the evaluated object C, and $f_{\mathrm{A}}\left(R-C\right)$ denotes the features of the area of the evaluated object C to erase reference object R. The improved model considers location differences and eases restrictions on feature selection. The range of $S_{\mathrm{O}}$ is 0 to 1. If the extracted and reference objects overlapped completely, then $S_{\mathrm{O}}=1$. If there is no overlap between the two objects, then $S_{\mathrm{O}}=0$.

Computing object similarity using a single feature will result in uncertain accuracy values. A natural solution is to apply multiple features to calculate object similarity. To this end, the object comprehensive similarity $S^{\prime }$ is defined as

$$S^{\prime }=\{\begin{array}{ll}0& if{T}_{\mathrm{C}}\ne T_{\mathrm{R}}\\ \frac{1}{N}{\displaystyle \sum _{i=1}^N{u}_i{S}_i}& otherwise\end{array}$$

(12)

where $T_{\mathrm{C}}$ and $T_{\mathrm{R}}$ denote the classes of the evaluation and its matching reference objects, respectively, $N$ is the number of features, $S_i$ denotes the object similarity using the ith feature, and $u_i$ is the weight of $S_i$. The feature weight is determined according to the real scenario, and the determination basis can be human subjectivity or feature applicability.

After computing the similarity of each evaluated object, the overall accuracy $S_{\mathrm{overall}}$ for object extraction can be calculated by

$$S_{\mathrm{overall}}={\displaystyle \sum _{j=1}^M{w}_j{S}_j^{\prime }}$$

(13)

where $S_j^{\prime }$ is the calculated similarity of the jth evaluated object, $M$ is the number of evaluated objects, and $w_j$ denotes the weight of jth evaluation object. The ratio of the area of the evaluated object to the sum of the area of all objects can be used as the object weight.

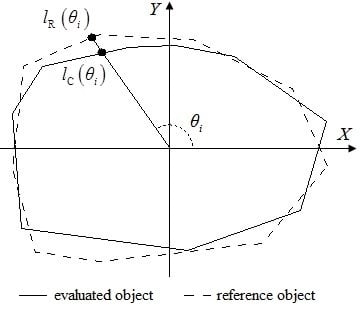
2.5. Distance-Based Accuracy Measures

The distance difference between two objects, which can be completely reflected by the boundary distribution, is an essential aspect to evaluate the similarity between objects. Particularly, Pratt introduced a figure of merit ($F_{\mathrm{FOM}}$) model to evaluate the accuracy of image segmentation [33]. $F_{\mathrm{FOM}}$ is defined as follows:

$$F_{\mathrm{FOM}}=\frac{1}{\max \left\{l_{\mathrm{C}},l_{\mathrm{R}}\right\}}{\displaystyle \sum _{i=1}^{l_{\mathrm{C}}}\frac{1}{1+d_i^2}}$$

(14)

where $l_{\mathrm{C}}$ is the boundary pixel number of the evaluated object, $l_{\mathrm{R}}$ is the boundary pixel number of its matching reference object, and $d_i$ is the distance of the ith boundary pixel from the evaluated object to the corresponding pixel on the reference object’s boundary. Based on $F_{\mathrm{FOM}}$, the shape similarity $B_{\mathrm{D}}$ is defined as follows:

$$B_{\mathrm{D}}=\frac{1}{\max \left\{l_{\mathrm{C}},l_{\mathrm{R}}\right\}}{\displaystyle \sum _{i=1}^{l_{\mathrm{C}}}\frac{1}{1+\frac{d_i}{\max (r_{\mathrm{C}},r_{\mathrm{R}})}}}$$

(15)

where $r_{\mathrm{C}}$ and $r_{\mathrm{R}}$ are the radii of the circumcircles for the evaluation and reference objects, respectively.

Generally, the boundary of the extracted object cannot be strictly the same as that of the reference due to the error propagation during image interpretation. This phenomenon reduces the feasibility of using Equation (15). To improve the flexibility of $B_{\mathrm{D}}$, a tolerance is set to judge if the two objects are identical. The improved $B_{\mathrm{D}}$ is defined as

$$B_{\mathrm{D}}=\frac{1}{\max \left\{l_{\mathrm{C}},l_{\mathrm{R}}\right\}}{\displaystyle \sum _{i=1}^{l_{\mathrm{C}}}{f}_i},f_i=\{\begin{array}{ll}0& d_i\ge d_2\\ \frac{1}{1+\frac{d_i}{\max (r_{\mathrm{C}},r_{\mathrm{R}})}}& d_1<d_i<d_2\\ 1& d_i\le d_1\end{array}$$

(16)

where $d_1$ and $d_2$ are two thresholds. The value of $d_1$ represents the tolerance for random errors. If the distance $d_i$ is less than the threshold $d_1$, the distance $d_i$ can be tolerated. The value of the $d_2$ represents the unacceptable value of the error. If the distance $d_i$ is larger than the threshold $d_2$, there is no reference object boundary pixel that matches the ith boundary pixel of the evaluation object. In combination with application purposes, the values of $d_1$ and $d_2$ are determined by the size of the object and the spatial resolution of the image. The range of shape similarity is from 0 to 1. If all distances from boundary pixels of the objects to matching reference object boundary are within the tolerance range, then $B_{\mathrm{D}}=1$. If all boundary pixels of the objects are incorrectly extracted, then $B_{\mathrm{D}}=0$.

Equation (16) compares all pixels in the extracted and reference objects that lead to precise evaluation result as well as low computation efficiency. This process can be simplified by choosing boundary pixels at an equal interval range. The simplified shape similarity $B_{\mathrm{L}}$ is defined as follows:

$$B_{\mathrm{L}}=\left(1-\frac{{\displaystyle \sum _{i=1}^k\left|l_{\mathrm{C}}\left({\theta }_i\right)-l_{\mathrm{R}}\left({\theta }_i\right)\right|}}{kMin\left(r_{\mathrm{C}},r_{\mathrm{R}}\right)}\right)\left(1-\frac{d_{\mathrm{C}-\mathrm{R}}}{2Min\left(r_{\mathrm{C}},r_{\mathrm{R}}\right)}\right)$$

(17)

where $k$ is the direction number, $l_{\mathrm{C}}\left({\theta }_i\right)$ and $l_{\mathrm{R}}\left({\theta }_i\right)$ denote the distance between the evaluation and reference objects from the barycenter to the boundary along the direction ${\theta }_i$ respectively, and ${\theta }_i=\frac{i\ast 2\pi }{k}$. If the evaluation or reference object is a concave polygon, where there may be many boundary points along the direction ${\theta }_i$, $l_{\mathrm{C}}\left({\theta }_i\right)$ or $l_{\mathrm{R}}\left({\theta }_i\right)$ is replaced by the mean distance. $d_{\mathrm{C}-\mathrm{R}}$ is the distance between the evaluated object barycenter and reference object barycenter, respectively. The range of $B_{\mathrm{L}}$ is from 0 to 1. If all sampling boundary pixels of the objects overlap with the matching reference object boundary, then $B_{\mathrm{D}}=1$. If all evaluated objects have no matching reference objects, then $B_{\mathrm{D}}=0$. Before calculating the distance difference, the evaluated object is shifted to the gravity center of the reference object (see Figure 3).

The sample number of boundary pixel determines the assessment reliability as well as the computation efficiency. If the requirement for reliability is high, the number of samples should be appropriately increased. If the calculation speed needs to be increased, the number of samples should be appropriately reduced.

Considering object classes, the object extraction accuracy $B_{\mathrm{overall}}$ of the entire evaluation area can be calculated using Equation (18).

$$B_{\mathrm{overall}}={\displaystyle \sum _{j=1}^M{w}_j{B}_j^{\prime }},B_j^{\prime }=\{\begin{array}{ll}0& if{T}_{\mathrm{C},j}\ne T_{\mathrm{R},j}\\ B_j& otherwise\end{array}$$

(18)

where $T_{\mathrm{C},j}$ and $T_{\mathrm{R},j}$ denote the classes for the jth evaluated object and its matched reference objects, $B_j$ is the shape similarity of the jth evaluated object with its matched reference objects on one of the above shape similarities, $M$ is the number of evaluated objects, and $w_j$ denotes the weight of the jth evaluation object. The proportion of the area of the evaluated object to the total area of objects can be used as the object weight.

3. Experimental Results and Analysis

In this section, the performance of the presented method was validated on two object types (i.e., water and building), as they are representative of natural and artificial scenarios in general. Generally, the extraction performance of water is satisfactory because water has a distinct boundary feature compared to its surrounding pixels. Compared to water extraction, the building extraction results may contain more errors that lead to lower accuracy, due to the complex environment surrounding buildings. On the other hand, the building boundary is regular, while the water boundary is irregular. The experiments were conducted on a PC with an Intel Core2Quad processor at a clock speed of 1.80 GHz. MATLAB^® and ARCGIS^® were utilized to produce experimental results.

3.1. Data Description

Two QuickBird images were selected to validate the proposed method. One image, with a spatial resolution of 2.4 m per pixel and an area of 1200 × 1200 pixels, was acquired on 16 July 2009 over Wuhan, China (see Figure 4a). The study area located on the outskirts of the city was mainly covered by water, farmland, roads, and buildings. Another pan-sharpened image, with a spatial resolution of 0.61 m per pixel and an area of 400 × 400 pixels, was acquired on 2 May 2005 over Xuzhou, China (see Figure 5a). The second study area, locating near the city center, was mainly covered by buildings, roads, water, bare land, and grassland. Figure 4b and Figure 5b present two complete reference maps produced via manual interpretation.

3.2. Object Extraction

Satellite images are processed to generate objects that will be subsequently used to verify the performance of OBIA assessment measures. To this end, an improved watershed segmentation method [34] was applied. The advantage of this method is that it integrates the spectral information, texture feature and spatial relationships, which in turn makes it able to produce objects whose sizes are closer to the true sizes. Once the segmentation results were obtained, object features, including the geometric characteristic, modified normalized difference water index (WNDWI) and normalized difference vegetation index (NDVI), were computed. Finally, the decision tree [35] using object features as input was performed to classify the image into target and background classes. The classification results are shown in Figure 4c and Figure 5c, respectively.

3.3. Evaluation of Object Extraction Accuracy Using Different Measures

The accuracy assessment is carried out by comparing extracted results with reference data, as shown in Figure 4d and Figure 5d. In this paper, the accuracy assessment employs all objects rather than a fixed number of test samples.

The object extraction accuracies of two classes are firstly evaluated by the area-based measurement, and

Table 1. Object extraction evaluation in terms of the area-based measurement.

Class	Correctness (%)	Completeness (%)	Quality (%)
Water	93.55	89.09	83.94
Building	76.34	83.84	66.55

reports the evaluation results. It can be seen that the water class performs better than the building class. The reason is that water is easily separated from background due to the relatively large spectral difference between water and the surrounding objects. However, both material change of the buildings rooves and the spectral similarity of buildings and their nearby objects decrease the extraction performance. The different performances of water and building classes is shown in Table 1, indicating that the area-based accuracy measure can assess OBIA accuracy in a straightforward and efficient manner.

In the second experiment, an accuracy evaluation was conducted using the object number-based accuracy index. To this end, numbers of total, correct, incorrect, and missing objects need to be computed in advance. As in the first experiment, the object matching method is able to judge whether objects are extracted correctly. With such automatic object extraction methods, it is extremely difficult to achieve accurate results. To assess the precision characteristic based on the object number, different object matching thresholds are set to judge if the object is extracted correctly.

Table 2. Object extraction evaluation using the object number-based measurement.

Class	Threshold	Correct Number	Correct Rate (%)	False Rate (%)	Missing Rate (%)
Water	0.90	38	56.72	43.28	46.48
	0.85	55	82.09	17.91	22.54
	0.80	63	94.03	5.97	11.27
Building	0.90	4	9.30	90.70	90.48
	0.85	21	48.84	51.16	50.00
	0.80	31	72.09	27.91	26.19

reports the evaluation results. The water class has a generally better performance than the building class, indicating that the object number-based index can reflect the OBIA performance. Table 2 also shows that the choice of threshold value has a profound impact on the number of correctly identified objects. If the threshold value is high, the correct number is low; conversely, a low threshold value leads to a high correct rate. Thus, the threshold can be taken as a guideline for users to measure the confidence level. That is, if objects with high confidence are required, the threshold should be set to a large value.

Geometric features can effectively reflect the characteristics of an object. This experiment validates its potential in evaluating OBIA results. To this end, area and perimeter are selected to measure the feature similarity between the extracted and reference objects. In this experiment, weights of area and perimeter are set as 0.67 and 0.33, respectively, by trial and error. The size similarity is calculated using Equations (8), (12), and (13), the improved size similarity is calculated using Equations (9), (12), and (13), and the matching similarity is calculated using Equations (11)–(13), as shown in

Table 3. Assessing quality in terms of similarity.

Class	Index	Size Similarity (%)	Improved Size Similarity (%)	Matching Similarity (%)
Water	Area	84.86	82.57	77.09
	Perimeter	89.12	87.88	58.92
	Area and perimeter	86.28	84.34	71.04
Building	Area	79.19	73.74	66.21
	Perimeter	81.16	78.55	55.55
	Area and perimeter	79.85	75.34	62.66

. The evaluation results indicate similar trends in different similarity measures for the two experimental areas. Similar to other assessment measures, all the similarity accuracies for the Xuzhou area are lower than those for the Wuhan area. The size similarity and improved size similarity in terms of area are both lower than those in terms of perimeter. However, matching similarity in terms of area is higher than that in terms of perimeter. For both the area and perimeter as assessment measures, the size similarity is always higher than the improved size similarity and the matching similarity is the lowest. This difference stems from the size similarity and improved size similarity, which do not consider the positional differences. The matching similarity considers the positional difference between the evaluated object and the reference data, which better reflects the similarity of features. The similarities of objects, calculated using different methods and features, differ, and the accuracy (based on similarity) also contains great uncertainty. To obtain stable evaluation results, more features should be considered to calculate the similarity.

The Euclidean distance between the gravity centers is used to calculate the distance between the evaluated object and its matching reference object. Thresholds $d_1$ and $d_2$ are set to the width of a pixel and five pixels, respectively. The shape similarity is calculated using Equations (16) and (18), and the improved shape similarity is estimated using Equations (17) and (18), as shown in

Table 4. Assessing quality in terms of distance.

Class	Shape Similarity (%)	Improved Shape Similarity (%)
Water	85.50	85.90
Building	76.46	77.99

. In the two experimental areas, the similarity based on boundary distance is slightly higher than that based on boundary difference and barycenter distance. The precision of object extraction is relatively high in the Wuhan area, which can be attributed to the similarity based on boundary distance being very close to that based on boundary difference and barycenter distance. Both similarities are calculated by comparing the detailed differences in objects, which fully reflects the differences in objects and ensures that the assessment measures are more stable. Although they require a tedious calculation process, these two measures need to be considered when assessing the accuracy of object extraction requiring high precision.

A comprehensive comparison of the object extraction for the two experimental areas is generated using Table 1, Table 2, Table 3 and Table 4. According to the comprehensive comparison, we can conclude that the water extraction result is generally better than the building extraction result. The superior results are due to the greater spectral difference between water and its surrounding objects than that between buildings and their surrounding objects, especially as the interior pixels of water have high homogeneity and building structures are complex.

4. Discussion

This paper presents four kinds of accuracy measures based on different object characteristics, namely, area-based, object number-based, feature similarity-based, and distance-based accuracy measures. Since the study area is usually large, a suitable sampling method needs to be selected before assessing the accuracy. The accuracy assessment results using object area are similar to those at the pixel level. Accuracy assessment based on object number requires that the objects are first extracted correctly. The criteria used to check if the objects are correctly or falsely identified have a profound impact on the assessment results. Many characteristics can be used as the basis of assessment measures for object feature similarity. The selection of a base has a significant impact on the assessment results: unreasonable feature selection will lead to unreliable assessment results (such as when only perimeter or length is used, or equal weights are used for area and perimeter). Thus, feature selection and feature weight are essential to determine the optimal basis.

The computation of difference-based accuracy measures is relatively complex. Selecting boundary pixels at reasonable intervals can improve the computational efficiency while retaining the reliability of the assessment results. Both area- and object number-based accuracy measures ignore the object detail. By contrast, feature-based accuracy assessments do not directly judge an object to be correct or otherwise; this aspect can better reflect the feature difference between the extraction object and the reference object. The accuracy measures based on boundary/location difference consider details of the object and reflect the object local feature difference, resulting in more accurate and confident results. Each assessment measure has its own advantages and disadvantages. Thus, the measures should be selected carefully according to the requirements. Specifically, if the accuracy needs to be computed in near-real time, the area-based measure would be chosen. This is because the area-based accuracy measure is straightforward and does not require an object matching process. Despite some errors, considering the advantage of computational efficiency, area-based measures can be selected to obtain faster assessment results with fewer requirements. If object extraction accuracy and its confidence are required simultaneously, the object number-based accuracy measure is recommended, as the threshold of coincidence degree is related to the confidence level: the larger the threshold, the higher the confidence level. If object extraction accuracy is to be understood comprehensively, feature-based and distance-based accuracy measurements are advisable as they fully consider detailed information of the object, such as shape and size.

5. Conclusions

A series of factors influence the assessment of object extraction from remote sensing images, which makes a complete and general accuracy index difficult to obtain. To tackle this issue, this paper presents four novel assessment measures with different criteria. The designed measurements are highly generalizable and provide users with practical means to evaluate object extraction results according to their unique needs. The methods presented in this paper require static objects with clearly defined edges. Further investigation and experimentation into dynamic objects (e.g., moving clouds, cars, and ships) with fuzzy boundaries is strongly recommended. The accuracy for objects with indeterminate boundaries can be assessed by two means: (1) assuming that the determinate boundaries are assigned to an object with indeterminate boundaries; and (2) setting the tolerance for the uncertainty of object boundaries (for example, the accuracy can be obtained by calculating the shape similarity based on the tolerance of object boundary distance).