Next Article in Journal
Development of a System of Compatible Individual Tree Diameter and Aboveground Biomass Prediction Models Using Error-In-Variable Regression and Airborne LiDAR Data
Next Article in Special Issue
Triple-Frequency Code-Phase Combination Determination: A Comparison with the Hatch-Melbourne-Wübbena Combination Using BDS Signals
Previous Article in Journal
Retrieval of Hyperspectral Surface Reflectance Based on Machine Learning
Previous Article in Special Issue
Vertical Displacements Driven by Groundwater Storage Changes in the North China Plain Detected by GPS Observations
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 10
Issue 2
10.3390/rs10020324
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Combining GPS, BeiDou, and Galileo Satellite Systems for Time and Frequency Transfer Based on Carrier Phase Observations

by
Pengfei Zhang
1,2,3,
Rui Tu
1,3,4,*,
Rui Zhang
1,4,
Yuping Gao
1,2 and
Hongbin Cai
1,2
1
National Time Service Center, Chinese Academy of Sciences, Shu Yuan Road, Xi’an 710600, China
2
Key Laboratory of Time and Frequency Primary Standards, Chinese Academy of Sciences, Xi’an 710600, China
3
University of Chinese Academy of Sciences, Yu Quan Road, Beijing 100049, China
4
Key Laboratory of Precision Navigation Positioning and Timing Technology, Chinese Academy of Sciences, Xi’an 710600, China
*
Author to whom correspondence should be addressed.
Remote Sens. 2018, 10(2), 324; https://doi.org/10.3390/rs10020324
Submission received: 13 January 2018 / Revised: 13 February 2018 / Accepted: 18 February 2018 / Published: 22 February 2018
(This article belongs to the Special Issue Multi-Constellation Global Navigation Satellite Systems: Methods and Applications)
Browse Figures
Versions Notes

Abstract

:
The carrier-phase (CP) technique based on the Global Navigation Satellite System (GNSS) has proved to be a useful spatial tool for remote and precise time transfer. In order to improve the robustness and stability of the time transfer solution for a time link, a new CP approach based on a combination of GPS, BeiDou (BDS), and Galileo satellite systems is proposed in this study. The mathematical model for the obtained unique time transfer solution is discussed. Three GNSS stations that can track GPS, BeiDou, and Galileo satellites were used, and two time links are established to assess the performance of the approach. Multi-GNSS time transfer outperforms single GNSS by increasing the number of available satellites and improving the time dilution of precision. For the long time link, with a geodetic distance of 7537.5 km, the RMS value of the combined multi-system solution improves by 18.8%, 59.4%, and 35.0% compared to GPS-only, BDS-only, and Galileo-only, respectively. The average frequency stability improves by 12.9%, 62.3%, and 36.0%, respectively. For the short time link, with a geodetic distance of 4.7 m, the improvement after combining the three GNSSs is 6.7% for GPS-only, 52.6% for BDS-only, and 38.2% for Galileo-only.

Graphical Abstract

1. Introduction

Time and frequency transfer is a basic issue for the comparison of remote time and frequency laboratories. Since the 1980s, the Global Positioning System (GPS) operated by the United States has been used for time and frequency transfer based on the common view (CV) approach, which provides impetus to the application in the field of time and frequency [1,2]. With development of the International GNSS Service (IGS) products, particularly for satellite orbit and clock products [3,4], all in view (AV) and carrier phase (CP) approaches have been proposed for time and frequency transfer using GPS code and carrier phase observations [5,6]. These approaches exhibit a better performance compared to the CV approach. For this reason, the CP approach based on the Global Navigation Satellite System (GNSS) is a primary technique for time and frequency transfer in laboratories worldwide.
With the revitalized and fully operational Russian GLObal Navigation Satellite System (GLONASS) [7,8,9,10], research on combining GPS and GLONASS signals for precise time and frequency transfer is currently being increasingly undertaken by many scientific communities. The two constellations can improve the solution for the CV and CP approaches, particularly in the case of short data batches [11,12,13]. However, owing to the different signal modes for frequency division multiple access (FDMA) for the current GLONASS and code division multiple access (CDMA) for GPS, the effect of inter-frequency biases (IFBs) [11] and differential code-phase biases (DCPBs) [14] for GLONASS has resulted in limited exploitation of this satellite system combination for precise time and frequency transfer. In recent years, other satellite systems that use CDMA similar to GPS have been developed. China’s BeiDou Navigation Satellite System has been providing a continuous service since 27 December 2012, and it covers the entire Asia-Pacific region [15,16,17,18]. The European Galileo, which was initiated by the European Space Agency (ESA) and the European Commission in the early 1990s, has been well maintained [18,19,20], and provides an opportunity for time and frequency transfer based on a combination of the multi-system without the IFB effect. As of 2017, a preliminary service can be provided for the two emerging satellite systems. Figure 1 shows a 24-h ground track of the three satellite systems available on 10 September 2017. It can be noted that 14 BeiDou satellites, 17 Galileo satellites, and 32 GPS satellites can be actively tracked. This provides a rich GNSS signal resource for combining the multi-system for time and frequency transfer.
When using the multi-system for time and frequency transfer, particularly based on the CP approach, the same reference time scale of satellite clocks is required. However, each satellite navigation system has its own individual time scale. Galileo satellite clocks provide Galileo system time (GST) [20,21], BeiDou satellite clocks refer to BeiDou time (BDT) [22,23,24], and GPS satellite clocks are relative to GPS time (GPST) [25,26,27,28,29]. After the International GNSS Service (IGS) started the “Multi GNSS Experiment” (MGEX) in 2012, combined satellite orbit and clock products with the same time scale have been provided by several analysis centers, including the ESA, GFZ, GENS, and CODE [16,17], which support newly developed GNSSs such as Galileo and BeiDou [30,31,32,33]. Therefore, the products satisfy the requirements for combining GPS, BeiDou, and Galileo for precise time and frequency transfer based on the CP approach.
Therefore, in order to improve the robustness and stability of time transfer, we combine GPS, BeiDou, and Galileo to obtain one unique time transfer solution. The corresponding mathematical model of the CP approach is provided, and experiments on long and short time links are performed to assess the performance of the approach. The structure of the rest of this manuscript is organized as follows: Section 2 describes the principle of multi-system time and frequency transfer. Section 3 discusses the experimental design and data processing strategy for assessing the performance of the approach. The results and discussion are provided in Section 4, and Section 5 presents the conclusions of this study.

2. Mathematical Model

Generally, for precise time transfer based on the GNSS technique, external time and frequency signals are connected to a GNSS receiver, and the signals can drive the receiver to collect the different GNSS signals. In the case of GPS alone, the ionosphere-free combination can be used for the dual-frequency carrier phase and pseudo-range observations to eliminate the first-order effects of the ionosphere [34,35,36,37,38]. After the ionosphere-free combination is formed, the observation equation of the CP technique can be written as follows [39,40]:
P i G = ρ i G + c ( d t r G − d t i , s G ) + T t r o p + ε i , P G
L i G = ρ i G + c ( d t r G − d t i , s G ) + T t r o p + N G + ε i , L G
where superscript G denotes GPS; i is a particular satellite; P i G and L i G are the ionosphere-free combination of pseudorange and carrier phase in meters, respectively; ρ i G represents the geometric distance between the phase center of the satellite and receiver antenna; c is the speed of light; d t i , s G is the satellite clock offset; T t r o p is the tropospheric delay, which is unrelated to the satellite system; N G is the phase ambiguity in meters; ε i , P G and ε i , L G are noise errors for the pseudorange and carrier phase, respectively; and d t r G denotes the receiver clock offset, which is the clock difference between the external time and frequency reference and the GPS time scale. Considering the existence of hardware delays in the receiver, antenna, and cables when conveying the internal electrical signal, the receiver clock offset usually contains these delays, which can be calibrated in the area of the time and frequency transfer [41,42]. Therefore, this is not included in the present study.
Thus, based on Equations (1) and (2), similar equations can be derived for the BeiDou and Galileo satellite systems. In these equations, superscripts C and E denote the BeiDou and Galileo systems, respectively. In the case of time transfer based on an individual satellite system, there are three receiver clock offsets ( d t r G , d t r C , d t r E ), and all of them represent the difference between the common external time and frequency scale ( t ) and the satellite system time scale ( t s y s G , t s y s C , t s y s E ) [43]. The expression can be written as:
d t r G = t − t s y s G
d t r C = t − t s y s C
d t r E = t − t s y s E
In order to derive the methodology of tightly combined different GNSS signals for time transfer based on the CP technique, and provide one unique time transfer solution, it is necessary to estimate a receiver clock offset that refers to one common satellite system time scale. Separating individual receiver clocks introduces additional satellite system biases between GPS, BeiDou, and Galileo. The additional biases are commonly known as inter-s ystem biases (ISBs) [44,45,46].
Here, when selecting the GPS time scale as the common reference satellite time scale, the receiver clock offset in BeiDou and Galileo can be replaced with the sum of the GPS receiver clock offset and the corresponding ISBs value, respectively, which are given by the following equations:
d t r C = t − t s y s C = ( t − t s y s G ) + ( t s y s G − t s y s C ) = d t r G + I S B s y s G C
d t r E = t − t s y s E = ( t − t s y s G ) + ( t s y s G − t s y s E ) = d t r G + I S B s y s G E
Thus, the combined observation equation based on the CP technique for time and frequency transfer can be written as:
{ P i G = ρ i G + c ( d t r G − d t i , s G ) + T t r o p + ε i , P G L i G = ρ i G + c ( d t r G − d t i , s G ) + T t r o p + N G + ε i , L G P i C = ρ i C + c ( d t r G + I S B s y s G C − d t i , s C ) + T t r o p + ε i , P C L i C = ρ i C + c ( d t r G + I S B s y s G C − d t i , s C ) + T t r o p + N C + ε i , L C P i E = ρ i E + c ( d t r G + I S B s y s G E − d t i , s E ) + T t r o p + ε i , P E L i E = ρ i E + c ( d t r G + I S B s y s G E − d t i , s E ) + T t r o p + N E + ε i , Φ E
Therefore, the observation equation can be transformed, linearized, and expressed in a compact format as Equation (9), where V is the residual vector, A is the coefficient matrix of the parameters to be estimated, and L denotes the “observed minus computed”. The parameters to be estimated are summarized in Equation (10).
V = A ⋅ X ¯ − L
Thus, we can consider the estimated parameter vector X ¯ to be:
X ¯ = [ x , y , z , d t r G , I S B s y s G C , I S B s y s G E , T t r o p , N G , N C , N E ]
Among the parameters, the unique receiver clock offset, d t r G , is the most interesting quantity in the application of precise time transfer, which is jointly determined by the three satellite system observations. In the case of time transfer, two stations i and j , are equipped with their corresponding time and frequency references. Then, the value of the time transfer, Δ T i j , between the two references can be obtained using the following expression:
Δ T i j = t i − t j = d t r G ( i ) − d t r G ( j )

3. Data Processing

3.1. Experiment Design

In order to evaluate the performance of precise time and frequency transfer with the combined GPS, BeiDou, and Galileo satellite systems, it is preferable to devise an experiment that considers the length of the time link. Meanwhile, a multi-GNSS tracking station can receive satellite signals from the GPS, BeiDou, and Galileo satellite systems. Therefore, three multi-GNSS stations are selected at different time laboratories in Europe and Asia, as shown in Figure 2. Stations NTS1 and NTS2 (located at National Time Service Center (NTSC)) are linked to the UTC (NTSC) time and frequency reference, while Station BRUX (located at the Observatoire Royal de Belgique (ORB)) is connected with the UTC (ORB) time and frequency reference. The two time laboratories can provide the precise time and frequency reference for the stations, which support two output signals, i.e., a sinusoidal output (5 MHz or 10 MHz) and a one pps output [47]. The details of these three stations are listed in Table 1. Here, two time links can be established. The first is NTS1-BRUX, which spans over 7537.5 km, and presents a long baseline time link; the second is a short baseline time link, NTS1-NTS2, with a geodetic distance of only 4.7 m.
The long distance time link is typically met in the time transfer area, particularly for the application of UTC/TAI computation. It is difficult to assess the performance of the approach owing to the different variation characteristics of the two time and frequency references at the two ends of the time link [48,49]. Therefore, an experiment with a short time link is designed, where the two GNSS stations are equipped with a common time and frequency reference (UTC (NTSC)) to cancel-out this effect.

3.2. Data Processing Strategy of Combined Multi-GNSS

In order to evaluate the performance of the approach, we developed new time and frequency transfer software named PTTSol (precise time transfer solution), which also supports the GPS, BeiDou, and Gilileo satellite systems. In the combined multi-GNSS CP approach, GPS L1/L2, BeiDou B1/B2, and Galileo E1/E5a dual-frequency observations are used to establish their corresponding ionosphere-free combinations to eliminate the ionospheric effect. The cycle slips of carrier phase are detected by the geometry-free (GF) and Melbourne-Wübbena combination, which are performed according to each satellite system’s signal frequency [50,51,52]. Precise satellite orbit and clock products are obtained from the CODE MGEX analysis center [53,54], in which system time refers to the GPS system scale. Because of the same receiver clock offset for different GNSSs, most the observational error models for GPS can be utilized directly for other systems. The details of the observation models and data processing strategies are provided in Table 2. Here, it is necessary to discuss the method of estimating the ISB parameters, which can include the epoch-wise variable, piece-wise constant, and daily constant methods [52,55]. Compared with the latter two methods, the first is more suitable for rigorous data analysis in the case of time and frequency transfer. Considering that ISB parameters are closely related to the common receiver clock offset in the tightly combined GPS, BeiDou, and Galileo system for time transfer, we hence select the epoch-wise variable strategy to estimate the parameters.
The orbit accuracy of GEO satellites is inconsistent with that of the IGSO and MEO in the BeiDou constellation [16,30], which would affect the performance of time transfer. Thus, the observations from GEO satellites are not used in our multi-system data processing.

4. Results and Discussion

The first advantage of a combined multi-system is that it employs more satellites compared to a single satellite system. Figure 3 shows a typical example of the number of satellites for the multi-system at station NTS1 and BRUX. The horizontal axis (Epoch) represents the number of the epoch from Modified Julian Day (MJD) 58006 to MJD 58008 when the sampling rate is 30 s. For the 7° elevation cut-off, the mean number of satellites is 18.1 for the multi-system, 8.7 for GPS, 4.7 for BeiDou, and 4.7 for Galileo at station NTS1. Compared with GPS-only, the number of available satellites in the multi-system is almost doubled. The same is found at station BRUX, where the mean value increases from 9.4 (GPS-only) to 17.3 (multi-system). Combining these satellite systems increases the total number of available satellites, and raises the number of satellites above 30°, which can be less affected by the observed environment, and improves the satellite geometry distribution. Figure 4 shows an example sky plot for these three systems at one epoch. It should be noted that the number of satellites above 30° increases from five (GPS-only) to 12 (multi-system) at station NTS1, and from five (GPS-only) to 10 (multi-system) at station BRUX. In addition, this can increase the sky view, particularly in environments such as urban canyons and ravines. Regarding time transfer, the receiver clock offset is the parameter of the greatest interest, and the combined multi-system could improve the solution availability and accuracy by improving the tracking geometry with a reduction of the time dilution of precision (TDOP). As shown in Figure 5, the mean TDOP is clearly improved from 1.13 (GPS-only) to 0.54 (multi-system) at station NTS1, and from 0.81 (GPS-only) to 0.39 (multi-system) at station BRUX. It should be noted that some obstacles were located at the south side of the NTS1, which may have blocked some satellites.
Figure 6 shows the results of time transfer for the single- and multi-system solution for the two time links. The vertical axis (clock difference) represents the difference between the two receiver clock offsets at the two ends of a time link, which can be determined according to Equation (11). The NTS1-BRUX time link is on the left, and the NTS1-NTS2 time link is on the right. It should be noted that the variations of time transfer values agree well with the solutions for each scenario. Multi-system solution exhibits improved robustness compared to individual single-system solutions, particular for the BeiDou-only solution. Additionally, there are clear biases among the four solutions. The reasons for these biases are different. For GPS-only, BDS-only, and Galileo-only, the main reason for the biases is the different hardware delays in different receiver channels for different satellite systems, which can be calibrated in the time transfer campaign. The bias between the multi-system and GPS-only solution is partly caused by different coordinate values for one station [11,56]. In fact, although the station positions estimated by the multi-system and GPS-only are very close, there are still coordinate differences, which range from a mm to cm level in three coordinate components.
The two external time and frequency references are individually equipped with the two ends of one time link, which effects the performance evaluation for different time transfer scenarios, particularly for the long time link. Therefore, the root mean square (RMS) value for the smooth result is always employed [13]. Here, the Kalman smoothing method is used to provide the corresponding RMS values, which are given in Table 3. It is clearly seen that the multi-system solution contains lower noise compared to the single-system, particularly compared to the BDS-only and Galileo-only solutions. For the long time link, the multi-system solution is improved by 18.8%, 59.4%, and 35.0% compared to GPS-only, BDS-only, and Galileo-only, respectively. With respect to the short time link, even though it has been equipped with a common external time and frequency reference, the RMS value partly indicates the different performances of these scenarios. The corresponding multi-system solution is 14.3%, 53.8%, and 40.0% better compared to GPS-only, BDS-only, and Galileo-only, respectively. The standard deviation (STD) for the short time link has received more research attention, because in this situation, the clock difference contains only a few hardware delays, even though the values of the delays differ for different satellite systems in one time link, and the variations are stable in the short term. This can provide an external reference to verify the time transfer performance. Table 4 presents the statistical values for the short time link. In this case, the improvements gained from combining these three GNSSs are 6.7%, 52.6%, and 38.2% w.r.t. GPS-only, BDS-only, Galileo-only, respectively. These results are consistent with the RMS results for the short time link.
Long time link NTS1-BURX is equipped with two different time and frequency references. In this case, evaluating the performance of the time transfer approach is slightly complicated because of the absence of an absolute standard for comparison. Here, the Allan deviation is employed to obtain the frequency stability [11,12,13], which is also used to further assess the performance of the solutions for the four scenarios. Figure 7 presents the frequency stability of these solutions for long time link NTS1-BRUX. It is clear that the multi-system solution shows slight improvement over the GPS-only solution. Moreover, with respect to the results of BDS-only and Galileo-only, the multi-system solution provides a more stable result for long time link NTS1-BRUX. The Allan deviations at different average times (Tau) for the solutions for NTS1-BRUX are given in Table 5, and the percentage of multi-system stability improvement over individual systems within 10,000 s is shown in Figure 8. The improvement shown by the multi-system is more than 3.8%, and the average at different time intervals is 12.9% compared to GPS-only. For BeiDou-only, the multi-system shows a significant improvement. The minimum improvement is 49.5% and the average is 62.3%. For Galileo-only, the improvement is more than 18.2% at these time intervals, and the average is 36.0%.

5. Summary and Conclusions

This study presents an approach of combining the GPS, BeiDou, and Galileo satellite systems for time and frequency transfer based on carrier phase observations. A mathematical model is provided, and the two time links are established to assess the performance of the combined solution with respect to time link accuracy and frequency stability compared to single system solutions for the same time link.
The first advantage of combining GPS, BeiDou, and Galileo systems is an increased number of available satellites and improved satellite tracking geometry. The mean number of satellites increases from 8.7 for GPS-only, 4.7 for BeiDou-only, and 4.7 for Galileo-only, to 18.1 for the multi-system at station NTS1, particularly the number of satellites above 30°, which enables higher quality observations for determining the receiver clock offset parameter in precise time transfer. A similar conclusion is derived at station BRUX. Moreover, the combined multi-system can improve tracking geometry with a reduction in the TDOP. Compared to GPS-only, the TDOP for the multi-system decreases from 1.13 to 0.54 at station NTS1, and from 0.81 to 0.39 at station BRUX, which is an improvement of 52.2% and 51.9%, respectively.
The long and short time links are evaluated with respect to time transfer performance. In all cases, the multi-system generates less noise and a more stable result compared to the single systems. For long time link NTS1-BRUX, the noise in the time transfer value for the combination of the three GNSSs shows an improvement of 18.8%, 59.4%, and 35.0% compared to GPS-only, BDS-only, and Galileo-only, respectively. Moreover, time and frequency stability is slightly improved with the multi-system at different average times. The average improvement in the amplitude of time and frequency stability is 12.9%, 62.3%, and 36.0%, compared to GPS-only, BeiDou-only, and Galileo-only, respectively. As short time link NTS1-NTS2 contains a common external time and frequency reference, the variation in the STD of the receiver clock difference for the multi-system shows an improvement of 6.7%, 52.6%, and 38.2% compared to GPS-only, BDS-only, and Galileo-only, respectively.
To conclude, precise time and frequency transfer based on a combination of multiple satellite systems shows improved robustness and stability. Although the same type of receivers are used to evaluate the performance, the approach is actually applicable to inhomogeneous receivers. This is because whether the receiver types are the same or not, they all need to be calibrated to obtain the hardware delay in the area of time and frequency transfer. However, this study proposes only the first step of this research and several topics still require further investigation. For example, determining how to allocate the weights for individual satellite systems when the GPS, BeiDou, and Galileo systems are combined, because each system has its own character and accuracy [57]; how ISB affects the performance of the common multi-system receiver clock offset solution; and how hardware calibrates in the time link based on multi-system time and frequency transfer. With the continuous development of the BeiDou and Galileo satellite systems, further improvement in time and frequency transfers can be achieved using the multi-system solution.

Acknowledgments

The work was partly supported by the program of National Key Research and Development Plan of China (Grant No:2016YFB0501804), National Natural Science Foundation of China (Grant No:41504006, 41674034), and Chinese Academy of Sciences (CAS) programs of “Pioneer Hundred Talents” (Grant No:Y620YC1701), Light of the west joint scholar” (Grant No:Y507YR1203), and “The Frontier Science Research Project” (Grant No:QYZDB-SSW-DQC028).

Author Contributions

Pengfei Zhang, Rui Tu conceived and designed the experiments; Pengfei Zhang performed the experiments, analyzed the data, and wrote the paper under the supervision of Rui Tu; Rui Zhang, Yuping Gao, and Hongbin Cai contributed to discussions and revisions.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Allan, D.W.; Weiss, M. Accurate time and frequency transfer during common-view of a GPS satellite. In Proceedings of the 1980 IEEE Frequency Control Symposium, Philadelphia, PA, USA, 28–30 May 1980; pp. 334–356. [Google Scholar]
  2. Levandowski, W.; Azoubib, J.; Klepczynski, W.J. GPS: Primary tool for time transfer. Proc. IEEE 1999, 87, 163–172. [Google Scholar] [CrossRef]
  3. Beutler, G.; Rothacher, M.; Schaer, S.; Springer, T.A.; Kouba, J.; Neilan, R.E. The International GPS Service (IGS): an interdisciplinary service in support of Earth sciences. Adv. Space Res. 1999, 23, 631–635. [Google Scholar] [CrossRef]
  4. Senior, K.; Koppang, P.; Ray, J. Developing an IGS time scale. IEEE Trans. UFFC 2003, 50, 585–593. [Google Scholar] [CrossRef]
  5. Petit, G.; Jiang, Z. GPS All in View time transfer for TAI computation. Metrologia 2008, 45, 35–45. [Google Scholar] [CrossRef]
  6. Jiang, Z.; Petit, G. Combination of TWSTFT and GNSS for accurate UTC time transfer. Metrologia 2009, 46, 305–314. [Google Scholar] [CrossRef]
  7. Geng, J.; Shi, C. Rapid initialization of real-time PPP by resolving undifferenced GPS and GLONASS ambiguities simultaneously. J. Geod. 2017, 91, 361–374. [Google Scholar] [CrossRef]
  8. Cai, C.; Gao, Y. Modeling and assessment of combined GPS/GLONASS precise point positioning. GPS Solut. 2013, 17, 223–236. [Google Scholar] [CrossRef]
  9. Lou, Y.; Zheng, F.; Gu, S.; Wang, C.; Guo, H.; Feng, Y. Multi-GNSS precise point positioning with raw single-frequency and dual-frequency measurement models. GPS Solut. 2016, 20, 849–862. [Google Scholar] [CrossRef]
  10. Liu, T.; Yuan, Y.; Zhang, B.; Wang, N.; Tan, B.; Chen, Y. Multi-GNSS precise point positioning (MGPPP) using raw observations. J. Geod. 2017, 91, 253–268. [Google Scholar] [CrossRef]
  11. Defraigne, P.; Baire, Q. Combining GPS and GLONASS for time and frequency transfer. Adv. Space Res. 2011, 47, 265–275. [Google Scholar] [CrossRef]
  12. Jiang, Z.; Lewandowski, W. Use of GLONASS for UTC time transfer. Metrologia 2012, 49, 57–61. [Google Scholar] [CrossRef]
  13. Harmegnies, A.; Defraigne, P.; Petit, G. Combining GPS and GLONASS in all-in-view for time transfer. Metrologia 2013, 50, 277–287. [Google Scholar] [CrossRef]
  14. Geng, J.; Zhao, Q.; Shi, C.; Liu, J. A review on the inter-frequency biases of GLONASS carrier-phase data. J. Geod. 2017, 91, 329–340. [Google Scholar] [CrossRef]
  15. CSNO. BeiDou Navigation Satellite System Signal in Space Interface Control Document (Open Service Signal); Version 2.1; China Satellite Navigation Office: Beijing, China, 2016.
  16. Steigenberger, P.; Hugentobler, U.; Hauschild, A.; Montenbruck, O. Orbit and clock analysis of Compass GEO and IGSO satellites. J. Geod. 2013, 87, 515–525. [Google Scholar] [CrossRef]
  17. Gu, S.; Lou, Y.; Shi, C.; Liu, J. BeiDou phase bias estimation and its application in precise point positioning with triple-frequency observable. J. Geod. 2015, 89, 979–992. [Google Scholar] [CrossRef]
  18. Changsheng, C.; Yang, G.; Lin, P.; Wujiao, D. An analysis on combined GPS/COMPASS data quality and its effect on single point positioning accuracy under different observing conditions. Adv. Space Res. 2014, 54, 818–829. [Google Scholar]
  19. Paziewski, J.; Wielgosz, P. Accounting for Galileo-GPS inter-system biases in precise satellite positioning. J. Geod. 2015, 89, 81–93. [Google Scholar] [CrossRef]
  20. Hlaváč, R.; Lösch, M.; Luongo, F.; HAHN, J. Timing Infrastructure for Galileo System. In Proceedings of the 20th European Frequency and Time Forum, Braunschweig, Germany, 27–30 March 2006; pp. 391–398. [Google Scholar]
  21. Li, X.; Zhang, X.; Ren, X.; Fritsche, M.; Wickert, J.; Schuh, H. Precise positioning with current multi-constellation Global Navigation Satellite Systems: GPS, GLONASS, Galileo and BeiDou. Sci. Rep. 2015, 5, 1–14. [Google Scholar] [CrossRef] [PubMed]
  22. Han, C.; Yang, Y.; Cai, Z. BDS navigation satellite system and its timescales. Metrologia 2011, 48, S213–S218. [Google Scholar] [CrossRef]
  23. Caissy, M.; Agrotis, L.; Weber, G.; Hernandez-Pajares, M.; Hugentobler, U. Innovation: The International GNSS Real-Time Service. GPS World 2012, 23, 52–58. [Google Scholar]
  24. Tegedor, J.; Øvstedal, O.; Vigen, E. Precise orbit determination and point positioning using GPS, Glonass, Galileo and BeiDou. J. Geod. Sci. 2014, 4, 2081–9943. [Google Scholar] [CrossRef]
  25. Huang, G.W.; Zhang, Q. Quality variation of GPS satellite clocks on-orbit using IGS clock products. Adv. Space Res. 2013, 51, 978–987. [Google Scholar] [CrossRef]
  26. Huang, G.W.; Zhang, Q. Real-time clock offset prediction with an improved model. GPS Solut. 2014, 18, 95–104. [Google Scholar] [CrossRef]
  27. Wang, Y.P.; Lu, Z.P.; Qu, Y.; Li, L.; Wang, N. Improving prediction performance of GPS satellite clock bias based on wavelet neural network. GPS Solut. 2016, 21, 1–12. [Google Scholar] [CrossRef]
  28. Xu, B.; Wang, Y.; Yang, X. Navigation Satellite Clock Error Prediction Based on Functional Network. Neural Process. Lett. 2013, 38, 305–320. [Google Scholar] [CrossRef]
  29. Kouba, J.; Héroux, P. Precise Point Positioning Using IGS Orbit and Clock Product. GPS Solut. 2001, 5, 12–28. [Google Scholar] [CrossRef]
  30. Li, X.; Ge, M.; Dai, X.; Ren, X.; Fritsche, M.; Wickert, J.; Schuh, H. Accuracy and reliability of multi-GNSS real-time precise positioning: GPS, GLONASS, BeiDou, and Galileo. J. Geod. 2015, 89, 607–635. [Google Scholar] [CrossRef]
  31. Montenbruck, O.; Steigenberger, P.; Prange, L.; Deng, Z.; Zhao, Q.; Perosanz, F.; Romero, I.; Noll, C.; Stürze, A.; Weber, G.; et al. The Multi-GNSS Experiment (MGEX) of the International GNSS Service (IGS)–Achievements, prospects and challenges. Adv. Space Res. 2017, 59, 1671–1697. [Google Scholar] [CrossRef]
  32. Gioia, C.; Borio, D.; Angrisano, A.; Gaglione, S.; Fortuny-Guasch, J. A Galileo IOV assessment: measurement and position domain. GPS Solut. 2015, 19, 187–199. [Google Scholar] [CrossRef] [Green Version]
  33. Uhlemann, M.; Gendt, G.; Ramatschi, M.; Deng, Z. GFZ Global Multi-GNSS Network and Data Processing Results. In IAG 150 Years. International Association of Geodesy Symposia; Rizos, C., Willis, P., Eds.; Springer: Cham, Switzerland, 2015; Volume 143, pp. 673–679. [Google Scholar]
  34. Zhao, Q.; Wang, G.; Liu, Z.; Hu, Z.; Dai, Z.; Liu, J. Analysis of BeiDou satellite measurements with code multipath and geometry-free ionospheric-free combinations. Sensors 2016, 16, 123. [Google Scholar] [CrossRef] [PubMed]
  35. Najibi, N.; Jin, S. Physical reflectivity and polarization characteristics for snow and ice-covered surfaces interacting with GPS signals. Remote Sens. 2013, 5, 4006–4030. [Google Scholar] [CrossRef]
  36. Geng, J.; Shi, C.; Ge, M.; Dodson, A.H.; Lou, Y.; Zhao, Q.; Liu, J. Improving the estimation of fractional-cycle biases for ambiguity resolution in precise point positioning. J. Geod. 2012, 86, 579–589. [Google Scholar] [CrossRef]
  37. Hadas, T.; Krypiak-Gregorczyk, A.; Hernández-Pajares, M.; Kaplon, J.; Paziewski, J.; Wielgosz, P.; Garcia-Rigo, A.; Kazmierski, K.; Sosnica, K.; Sierny, J.; et al. Impact and implementation of higher-order ionospheric effects on precise GNSS applications. J. Geophys. Res. Solid Earth 2017, 122, 9420–9436. [Google Scholar] [CrossRef]
  38. Afifi, A.; El-Rabbany, A. Improved Between-Satellite Single-Difference Precise Point Positioning Model Using Triple GNSS Constellations: GPS, Galileo, and BeiDou. Positioning 2016, 7, 63–74. [Google Scholar] [CrossRef]
  39. Lu, C.; Li, X.; Zus, F.; Heinkelmann, R.; Dick, G.; Ge, M.; Wickert, J.; Schuh, H. Improving BeiDou real-time precise point positioning with numerical weather models. J Geod. 2017, 91, 1019–1029. [Google Scholar] [CrossRef]
  40. Kouba, J. A Guide to Using International GNSS Service (IGS) Products. Available online: http://acc.igs.org/UsingIGSProductsVer21.pdf (accessed on 3 February 2018).
  41. Esteban, H.; Palacio, J.; Javier, G.F.; Feldmann, T.; Bauch, A.; Piester, D. Improved GPS-Based Time Link Calibration Involving ROA and PTB. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2010, 57, 714–720. [Google Scholar] [CrossRef] [PubMed]
  42. Rovera, G.D.; Torre, J.M.; Sherwood, R.; Abgrall, M.; Courde, C.; Laas-Bourez, M.; Uhrich, P. Link calibration against receiver calibration: an assessment of GPS time transfer uncertainties. Metrologia 2014, 51, 476–490. [Google Scholar] [CrossRef]
  43. Afifi, A.; El-Rabbany, A. Performance Analysis of Several GPS/Galileo Precise Point Positioning Models. Sensors 2015, 15, 14701–14726. [Google Scholar] [CrossRef] [PubMed]
  44. Torre, A.D.; Caporali, A. An analysis of inter-system biases for multi-GNSS positioning. GPS Solut. 2015, 19, 297–307. [Google Scholar] [CrossRef]
  45. Yuan, Y.; Zhang, B. Retrieval of inter-system biases (ISBs) using a network of multi-GNSS receivers. J. Glob. Position Syst. 2014, 13, 22–29. [Google Scholar]
  46. Nadarajah, N.; Teunissen, P.J.G.; Raziq, N. Beidou inter-satellite-type bias evaluation and calibration for mixed receiver attitude determination. Sensors 2013, 13, 9435–9463. [Google Scholar] [CrossRef] [PubMed]
  47. Fridelance, P.; Samain, E.; Veillet, C. T2L2-Time transfer by Laser link: A new optical time transfer generation. Exp. Astron. 1997, 7, 191–207. [Google Scholar] [CrossRef]
  48. Jiang, Z.; Czubla, A.; Nawrocki, J.; Lewandowski, W.; Arias, E.F. Comparing a GPS time link calibration with an optical fiber self-calibration with 200ps accuracy. Metrologia 2015, 52, 384–391. [Google Scholar] [CrossRef]
  49. Panfilo, G.; Tavella, P. Atomic clock prediction based on stochastic differential equations. Metrologia 2008, 45, 108–116. [Google Scholar] [CrossRef]
  50. Lin, P.; Li, X.; Zhang, X.; Li, X.; Lu, C.; Zhao, Q.; Liu, J. Considering Inter-Frequency Clock Bias for BDS Triple-Frequency Precise Point Positioning. Remote Sens. 2017, 9, 734. [Google Scholar] [CrossRef]
  51. Guo, F.; Zhang, X.; Wang, J.; Ren, X. Modeling and assessment of triple-frequency BDS precise point positioning. J. Geod. 2016, 90, 1223–1235. [Google Scholar] [CrossRef]
  52. Odijk, D.; Teunissen, P.J.G. Characterization of between-receiver GPS-Galileo inter-system biases and their effect on mixed ambiguity resolution. GPS Solut. 2013, 17, 521–533. [Google Scholar] [CrossRef]
  53. Arnold, D.; Meindl, M.; Beutler, G.; Dach, R.; Schaer, S.; Lutz, Z.; Prange, L.; Sośnica, K.; Mervart, L.; Jäggi, A. CODE’s new solar radiation pressure model for GNSS orbit determination. J. Geod. 2015, 89, 775–791. [Google Scholar] [CrossRef] [Green Version]
  54. Prange, L.; Orliac, E.; Dach, R.; Arnold, D.; Beutler, G.; Schaer, S.; Jäggi, A. CODE’s five-system orbit and clock solution—The challenges of multi-GNSS data analysis. J. Geod. 2017, 91, 345–360. [Google Scholar] [CrossRef]
  55. Jiang, N.; Xu, Y.; Xu, T.; Xu, G.; Sun, Z.; Schuh, H. GPS/BDS short-term ISB modeling and prediction. GPS Solut. 2017, 21, 163–175. [Google Scholar] [CrossRef]
  56. Yao, J.; Skakun, I.; Jiang, Z.; Levine, J. A detailed comparison of two continuous GPS carrier-phase time transfer techniques. Metrologia 2015, 52, 666–676. [Google Scholar] [CrossRef]
  57. Kazmierski, K.; Sośnica, K.; Hadas, T. Quality assessment of multi-GNSS orbits and clocks for real-time precise point positioning. GPS Solut. 2018, 22. [Google Scholar] [CrossRef]
Remotesensing 10 00324 g001a 550Remotesensing 10 00324 g001b 550
Figure 1. Ground tracks of three satellite navigation systems as of September 2017: from top to bottom, BeiDou (a); Galileo (b); and GPS (c).
Figure 1. Ground tracks of three satellite navigation systems as of September 2017: from top to bottom, BeiDou (a); Galileo (b); and GPS (c).
Remotesensing 10 00324 g001aRemotesensing 10 00324 g001b
Remotesensing 10 00324 g002 550
Figure 2. Geographical distribution of used multi-GNSS stations.
Figure 2. Geographical distribution of used multi-GNSS stations.
Remotesensing 10 00324 g002
Remotesensing 10 00324 g003 550
Figure 3. Comparisons of the number of satellites for the CP technique in single- and multi-system modes at stations NTS1 (left) and BRUX (right).
Figure 3. Comparisons of the number of satellites for the CP technique in single- and multi-system modes at stations NTS1 (left) and BRUX (right).
Remotesensing 10 00324 g003
Remotesensing 10 00324 g004 550
Figure 4. Comparisons of CP sky plots (azimuth vs. elevation) of three GNSSs (black = GPS, blue = BeiDou, red = Galileo) at stations NTS1 (left) and BRUX (right) at the epoch of the maximum number of satellites.
Figure 4. Comparisons of CP sky plots (azimuth vs. elevation) of three GNSSs (black = GPS, blue = BeiDou, red = Galileo) at stations NTS1 (left) and BRUX (right) at the epoch of the maximum number of satellites.
Remotesensing 10 00324 g004
Remotesensing 10 00324 g005 550
Figure 5. Comparisons of TDOP for the CP technique in single- and multi-system modes at stations NTS1 (left) and BRUX (right).
Figure 5. Comparisons of TDOP for the CP technique in single- and multi-system modes at stations NTS1 (left) and BRUX (right).
Remotesensing 10 00324 g005
Remotesensing 10 00324 g006 550
Figure 6. Result of time transfer in single- and multi-system modes for the two time links. The left is long distance time link NTS1-BRUX, and the right is short distance time link NTS1-NTS2.
Figure 6. Result of time transfer in single- and multi-system modes for the two time links. The left is long distance time link NTS1-BRUX, and the right is short distance time link NTS1-NTS2.
Remotesensing 10 00324 g006
Remotesensing 10 00324 g007 550
Figure 7. Comparison of Allan deviations for the four approaches for NTS1-BRUX.
Figure 7. Comparison of Allan deviations for the four approaches for NTS1-BRUX.
Remotesensing 10 00324 g007
Remotesensing 10 00324 g008 550
Figure 8. Percentage improvement in the stability of multi-system frequency over the single systems within 10,000s.
Figure 8. Percentage improvement in the stability of multi-system frequency over the single systems within 10,000s.
Remotesensing 10 00324 g008
Table
Table 1. Detailed information of the used stations.
Table 1. Detailed information of the used stations.
Site NameTime Lab.Frequency StandardGNSS ReceiverAntenna
NTS1NTSCUTC (NTSC)SEPT POLARX4TRSEPCHOKE_MC
NTS2NTSCUTC (NTSC)SEPT POLARX4TRSEPCHOKE_MC
BRUXORBUTC (ORB)SEPT POLARX4TRJAVRINGANT_DM
Table
Table 2. Observation models and multi-system RINEX data processing strategies.
Table 2. Observation models and multi-system RINEX data processing strategies.
ItemsModels and Strategies
ObservationsUndifferenced carrier phase and code observation
Signal selectionGPS:L1/L2; BeiDou: B1/B2; Galileo: E1/E5a
Satellite orbit and clockUsing the precise satellite products from CODE
Satellite antenna phase centerCorrected using MGEX value
Ionosphere Eliminated by ionosphere-free combination
Tropospheric delayInitial model + random-walk process
Elevation cutoff7°
Sampling rate30 s
Observation weightElevation dependent weight
EstimatorLSQ in sequential mode
Receiver clock offsetEstimated with white noise
ISBEstimated with epoch-wise variable method
Phase wind-up effectModel corrected
Table
Table 3. Time link residuals compared with Kalman filter smoothing values (units: nanoseconds).
Table 3. Time link residuals compared with Kalman filter smoothing values (units: nanoseconds).
Time linkMultiGPSBDSGalileo
NTS1-BRUX0.0130.0160.0320.020
NTS1-NTS20.0060.0070.0130.010
Table
Table 4. Statistical values for the short time link (units: nanoseconds).
Table 4. Statistical values for the short time link (units: nanoseconds).
ItemMultiGPSBDSGalileo
STD0.0550.0590.1160.089
Mean154.177154.184151.201153.555
Table
Table 5. Allan deviations for the four methods in real-time mode for NTS1-BRUX.
Table 5. Allan deviations for the four methods in real-time mode for NTS1-BRUX.
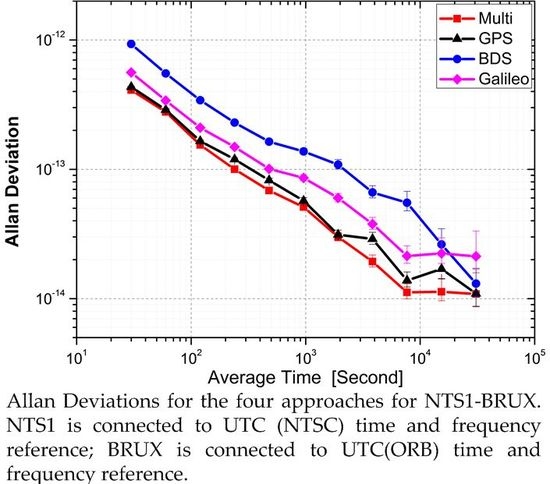
TauMultiGPSBDSGalileo
304.10 × 10−134.33 × 10−139.31 × 10−135.61 × 10−13
602.78 × 10−132.89 × 10−135.51 × 10−133.40 × 10−13
1201.54 × 10−131.65 × 10−133.42 × 10−132.10 × 10−13
2401.00 × 10−131.20 × 10−132.30 × 10−131.49 × 10−13
4806.86 × 10−148.23 × 10−141.64 × 10−131.01 × 10−13
9605.10 × 10−145.71 × 10−141.37 × 10−138.58 × 10−14
19203.00 × 10−143.12 × 10−141.09 × 10−136.01 × 10−14
38401.93 × 10−142.89 × 10−146.63 × 10−143.78 × 10−14
76801.12 × 10−141.38 × 10−145.52 × 10−142.14 × 10−14
15,3601.13 × 10−141.70 × 10−142.62 × 10−142.24 × 10−14
30,7201.09 × 10−141.09 × 10−141.31 × 10−142.13 × 10−14

Share and Cite

MDPI and ACS Style

Zhang, P.; Tu, R.; Zhang, R.; Gao, Y.; Cai, H. Combining GPS, BeiDou, and Galileo Satellite Systems for Time and Frequency Transfer Based on Carrier Phase Observations. Remote Sens. 2018, 10, 324. https://doi.org/10.3390/rs10020324

AMA Style

Zhang P, Tu R, Zhang R, Gao Y, Cai H. Combining GPS, BeiDou, and Galileo Satellite Systems for Time and Frequency Transfer Based on Carrier Phase Observations. Remote Sensing. 2018; 10(2):324. https://doi.org/10.3390/rs10020324

Chicago/Turabian Style

Zhang, Pengfei, Rui Tu, Rui Zhang, Yuping Gao, and Hongbin Cai. 2018. "Combining GPS, BeiDou, and Galileo Satellite Systems for Time and Frequency Transfer Based on Carrier Phase Observations" Remote Sensing 10, no. 2: 324. https://doi.org/10.3390/rs10020324

APA Style

Zhang, P., Tu, R., Zhang, R., Gao, Y., & Cai, H. (2018). Combining GPS, BeiDou, and Galileo Satellite Systems for Time and Frequency Transfer Based on Carrier Phase Observations. Remote Sensing, 10(2), 324. https://doi.org/10.3390/rs10020324

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop