Using Satellite Error Modeling to Improve GPM-Level 3 Rainfall Estimates over the Central Amazon Region
Abstract
:1. Introduction
2. Study Area, Data, and Methodology
- One National Institute of Meteorology (INMET) rain gauge located in Manaus city (at 3.1°S and 60.0°W). The INMET rain gauge is an automatic station that provides hourly records. This study uses a period of 30 years of daily accumulations (mm∙day−1);
- The S-band SIPAM radar rainfall estimates, processed by Texas A&M University. The rainfall estimates were obtained through the Constant Altitude Plan Position Indicator (CAPPI) product at a 2.5 km vertical level. The radial data were initially gridded to a Cartesian grid with 2 km × 2 km × 0.5 km resolution every 12 min. However, to match the satellite product, the radar rainfall retrievals were integrated to 30 min and averaged to 0.1 degrees. To reduce the uncertainties of the radar rainfall retrievals, the following criteria were adopted: (i) a radar coverage area of 30–110 km in radius was adopted because of radar physical limitations in detecting signals directly above it (“cone of silence”) and far at the constant altitude of 2.5 km; (ii) the areas where the radar beam was blocked by nearby objects were masked out. We refer the reader to Oliveira et al. [10] for a more detailed description of the S-band SIPAM radar and IMERG rainfall retrievals and their performance over the study region;
- The Integrated Multisatellite Retrievals for GPM (IMERG)—GPM Level 3 rainfall estimates (V03D, Final run version). The IMERG Final run (research) product is a quasi-global (60° N–S) dataset, with 0.1°/30 min spatial/temporal resolution and currently available for March 2014–present [14,15]. Although newer versions of this product have and will become available, the methodology developed in this work can be easily adapted to any future version of IMERG. By choosing the Final run, which includes a monthly gauge adjustment, we present here the best-case scenario in terms of errors associated with the IMERG product and the worst-case scenario in terms of error correction with PUSH. In other words, the correction scheme would have more room for improvement and look more impressive if applied to the Late or Early near-real-time runs, which lack the bias adjustment.
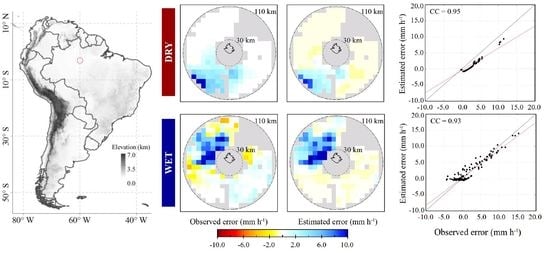
3. Results
3.1. Model Calibration
3.2. Model Performance
3.3. Satellite Precipitation Product Correction
4. Discussion
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Espinoza, C.; Marengo, J.A.; Ronchail, J.; Carpio, J.M.; Flores, L.N.; Guyot, J.L. The extreme 2014 flood in south-western Amazon basin, the role of tropical-subtropical South Atlantic SST gradient. Environ. Res. Lett. 2014, 9, 124007. [Google Scholar] [CrossRef] [Green Version]
- Falck, A.S.; Maggioni, V.; Tomasella, J.; Vila, D.A.; Diniz, F.L.R. Propagation of satellite precipitation uncertainties through a distributed hydrologic model: A case study in the Tocantins-Araguaia basin in Brazil. J. Hydrol. 2014, 527, 943–957. [Google Scholar] [CrossRef]
- de Oliveira, N.S.; Rotunno Filho, O.C.; Marton, E.; Silva, C. Correlation between rainfall and landslides in Nova Friburgo, Rio de Janeiro-Brazil: A case study. Environ. Earth Sci. 2016, 75, 1358. [Google Scholar] [CrossRef]
- Hong, Y.; Hsu, K.-L.; Moradkhani, H.; Sorooshian, S. Uncertainty quantification of satellite precipitation estimation and monte carlo assessment of the error propagation into hydrologic response. Water Resour. Res. 2006, 42, 1–15. [Google Scholar] [CrossRef]
- Tang, L.; Tian, Y.; Yan, F.; Habib, E. An improved procedure for the validation of satellite-based precipitation estimates. Atmos. Res. 2015, 163, 61–73. [Google Scholar] [CrossRef]
- Tian, Y.; Huffman, G.J.; Adler, R.F.; Tang, L.; Sapiano, M.; Maggioni, V.; Wu, H. Modeling errors in daily precipitation measurements: Additive or multiplicative? Geophys. Res. Lett. 2013, 40, 2060–2065. [Google Scholar] [CrossRef]
- Tian, Y.; Peters-Lidard, C.; Eylander, J.; Joyce, R.; Huffman, G.; Adler, R.; Hsu, K.; Turk, F.; Garcia, M. Component analysis of errors in satellite-based precipitation estimates. J. Geophys. Res. 2009, 114, D24101. [Google Scholar] [CrossRef]
- Maggioni, V.; Sapiano, M.; Adler, R.; Tian, Y.; Huffman, G. An error model for uncertainty quantification in high-time-resolution precipitation products. J. Hydrometeorol. 2014, 15, 1274–1292. [Google Scholar] [CrossRef]
- Maggioni, V.; Sapiano, M.R.P.; Adler, R.F. Estimating uncertainties in high-resolution satellite precipitation products: Systematic or random error? J. Hydrometeorol. 2016, 17, 1119–1129. [Google Scholar] [CrossRef]
- Oliveira, R.; Maggioni, V.; Vila, D.; Morales, C. Characteristics and diurnal cycle of GPM rainfall estimates over the central Amazon region. Remote Sens. 2016, 8, 544. [Google Scholar] [CrossRef]
- Burleyson, C.; Feng, Z.; Hagos, S.; Fast, J.; Machado, L.; Martin, S. Spatial Variability of the Background Diurnal Cycle of Deep Convection around the GoAmazon2014/5 Field Campaign Sites. J. Appl. Meteorol. Climatol. 2016. [Google Scholar] [CrossRef]
- Giangrande, S.E.; Toto, T.; Jensen, M.P.; Bartholomew, M.J.; Feng, Z.; Protat, A.; Williams, C.R.; Schumacher, C.; Machado, L. Convective cloud vertical velocity and mass-flux characteristics from radar wind profiler observations during GoAmazon2014/5. J. Geophys. Res. Atmos. 2016, 121, 891–913. [Google Scholar] [CrossRef]
- Tang, S.; Xie, S.; Zhang, Y.; Zhang, M.; Schumacher, C.; Upton, H.; Jensen, M.P.; Johnson, K.L.; Wang, M.; Ahlgrimm, M.; et al. Large-scale vertical velocity, diabatic heating and drying profiles associated with seasonal and diurnal variations of convective systems observed in the GoAmazon2014/5 experiment. Atmos. Chem. Phys. 2016, 16, 14249–14264. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Braithwaite, D.; Hsu, K.; Joyce, R.; Xie, P. GPM Integrated Multi-Satellite Retrievals for GPM (IMERG) Algorithm Theoretical Basis Document (ATBD); National Aeronautics and Space Administration (NASA): Washington, DC, USA, 2015. Available online: http://pmm.nasa.gov/sites/default/files/document_files/IMERG_ATBD_V4.4.pdf (accessed on 10 August 2016).
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J. Integrated Multi-Satellite Retrievals for GPM (IMERG) Technical Documentation; National Aeronautics and Space Administration (NASA): Washington, DC, USA, 2015. Available online: http://pmm.nasa.gov/sites/default/files/document_files/IMERG_doc.pdf (accessed on 10 August 2016).
- Machado, L.A.T.; Silva Dias, M.A.F.; Morales, C.; Fisch, G.; Vila, D.; Albrecht, R.; Goodman, S.J.; Calheiros, A.J.P.; Biscaro, T.; Kummerow, C.; et al. The CHUVA Project. How Does Convection Vary across Brazil? Bull. Am. Meteorol. Soc. 2014, 95, 1365–1380. [Google Scholar] [CrossRef]
- Martin, S.T.; Artaxo, P.; Machado, L.A.T.; Manzi, A.O.; Souza, R.A.F.; Schumacher, C.; Wang, J.; Andreae, M.O.; Barbosa, H.M.J.; Fan, J.; et al. Introduction: Observations and Modeling of the Green Ocean Amazon (GoAmazon2014/5). Atmos. Chem. Phys. 2016, 16, 4785–4797. [Google Scholar] [CrossRef]
- Marengo, J.A.; Fisch, G.F.; Alves, L.M.; Sousa, N.V.; Fu, R.; Zhuang, Y. Meteorological context of the onset and end of the rainy season in Central Amazonia during the GoAmazon2014/5. Atmos. Chem. Phys. 2017, 17, 7671–7681. [Google Scholar] [CrossRef]
- Liebmann, B.; Marengo, J. Interannual variability of the rainy season and rainfall in the Brazilian Amazon Basin. J. Clim. 2001, 14, 4308–4318. [Google Scholar] [CrossRef]
- Machado, L.; Laurent, H.; Dessay, N.; Miranda, I. Seasonal and diurnal variability of convection over the Amazonia: A comparison of different vegetation types and large scale forcing. Theor. Appl. Climatol. 2004, 78, 61–77. [Google Scholar] [CrossRef]
- Satyamurty, P.; De Castro, A.A.; Tota, J.; Gularte, L.E.S.; Manzi, A.O. Rainfall trends in the Brazilian Amazon basin in the past eight decades. Theor. Appl. Climatol. 2010, 99, 139–148. [Google Scholar] [CrossRef]
- Santos, E.B.; Lucio, P.S.; Silva, C.M.S. Precipitation regionalization of the Brazilian Amazon. Atmos. Sci. Lett. 2015, 16, 185–192. [Google Scholar] [CrossRef]
- Villar, J.C.E.; Ronchail, J.; Guyot, J.L.; Cochonneau, G.; Naziano, F.; Lavado, W.; Oliveira, E.D.; Pombosa, R.; Vauchel, P. Spatio-temporal rainfall variability in the Amazon basin countries (Brazil, Peru, Bolivia, Colombia, and Ecuador). Int. J. Climatol. 2009, 29, 1574–1594. [Google Scholar] [CrossRef]
- Liebmann, B.; Camargo, S.J.; Seth, A.; Marengo, J.A.; Carvalho, L.M.; Allured, D.; Fu, R.; Vera, C.S. Onset and End of the Rainy Season in South America in Observations and the ECHAM 4.5 Atmospheric General Circulation Model. J. Clim. 2007, 20, 2037–2050. [Google Scholar] [CrossRef]
- Bombardi, R.J.; Carvalho, L.M.V. IPCC global coupled model simulations of the South America monsoon system. Clim. Dyn. 2009, 33, 893–916. [Google Scholar] [CrossRef]
- Coelho, C.A.S.; Cardoso, D.H.F.; Firpo, M.A.F. Precipitation diagnostics of an exceptionally dry event in Sao Paulo, Brazil. Theor. Appl. Climatol. 2016, 125, 769–784. [Google Scholar] [CrossRef]
- Taylor, K.E. Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
- Roebber, P.J. Visualizing multiple measures of forecast quality. Weather Forecast. 2009, 24, 601–608. [Google Scholar] [CrossRef]








| Periods | Time Steps | ||
|---|---|---|---|
| Calibration | Dry | 15 June 2014–21 December 2014 | 8043 |
| Wet | 22 December 2014–23 May 2015 | 6641 | |
| Validation | Dry | 24 May 2015–17 August 2015 | 3416 |
| Wet | 12 March 2014–14 June 2014 | 3865 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oliveira, R.; Maggioni, V.; Vila, D.; Porcacchia, L. Using Satellite Error Modeling to Improve GPM-Level 3 Rainfall Estimates over the Central Amazon Region. Remote Sens. 2018, 10, 336. https://doi.org/10.3390/rs10020336
Oliveira R, Maggioni V, Vila D, Porcacchia L. Using Satellite Error Modeling to Improve GPM-Level 3 Rainfall Estimates over the Central Amazon Region. Remote Sensing. 2018; 10(2):336. https://doi.org/10.3390/rs10020336
Chicago/Turabian StyleOliveira, Rômulo, Viviana Maggioni, Daniel Vila, and Leonardo Porcacchia. 2018. "Using Satellite Error Modeling to Improve GPM-Level 3 Rainfall Estimates over the Central Amazon Region" Remote Sensing 10, no. 2: 336. https://doi.org/10.3390/rs10020336
APA StyleOliveira, R., Maggioni, V., Vila, D., & Porcacchia, L. (2018). Using Satellite Error Modeling to Improve GPM-Level 3 Rainfall Estimates over the Central Amazon Region. Remote Sensing, 10(2), 336. https://doi.org/10.3390/rs10020336