Impact of Sea Ice Drift Retrieval Errors, Discretization and Grid Type on Calculations of Ice Deformation
Abstract
:1. Introduction
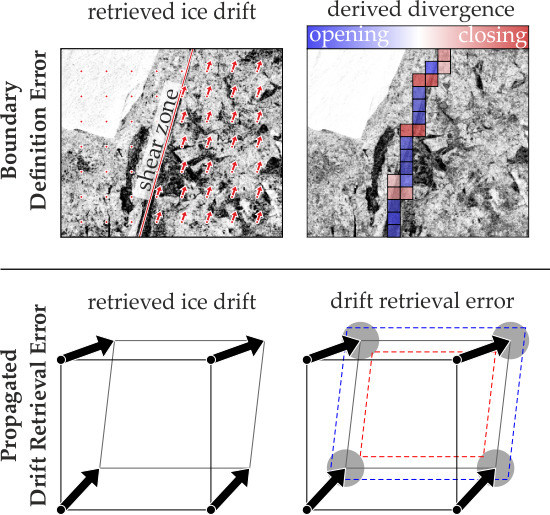
- Propagated drift retrieval error (PDRE): Based on the theory of error propagation one can estimate the statistical uncertainties of the deformation parameters caused by the uncertainties of the drift vectors [16]. For characterizing deformation, the three invariants divergence, shear, and vorticity are calculated based on the line integral around the boundary of a predefined grid cell. According to Lindsay and Stern [16], the error of the invariants is proportional to the error in area change caused by erroneous drift vectors. It depends on the number of drift vectors used for the calculation of the line integral, the size of the deformation cell, and the acquisition time gap of the successive SAR images. Lindsay and Stern [16], for example, estimated an error in divergence of 0.005 (0.5%) per day for a drift field given at a spatial resolution of 10 by 10 km and with a time gap between image acquisitions of 3 days (both typical for the RADARSAT Geophysical Processor System, RGPS), assuming a drift detection error of 0.1 km. Here, it should be noticed that the deformation error can be much higher when difficult tracking conditions are present or the temporal and spatial resolution changes. This is addressed in the discussion below.
- Boundary definition error (BDE): In the case of sea ice, deformation features often appear as distinct discontinuities in the drift field. Shear zones, e.g., are linear boundaries between ice floes drifting antiparallel relative to one other (see Figure 1). Pressure ridges occur if ice floes move towards each other. Vorticity reflects curvilinear motion and may indicate rotations of single ice floes. With only a few points defining the deformation cell, errors in the computed deformation parameters may be significant because boundaries between different drift zones in the presence of localized deformations such as leads or ridges may not be adequately represented [16]. This results in artificial deformation rates and a loss of invariance [16,17]. Figure 1 shows how the BDE results in artificial opening and closing when a shear zone runs through a regular deformation grid. The BDE may lead to misinterpretations of the derived deformation processes and affect statistics decisively.
2. Methods
2.1. Deformation Grid and Computation
2.2. Propagated Drift Retrieval Error
2.3. Boundary Definition Error
3. Results
3.1. Propagated Drift Retrieval Error
3.2. Boundary Definition Error
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Dierking, W. Sea Ice Monitoring by Synthetic Aperture Radar. Oceanography 2013, 26, 100–111. [Google Scholar] [CrossRef]
- Fily, M.; Rothrock, D.A. Opening and closing of sea ice leads: Digital measurements from synthetic aperture radar. J. Geophys. Res. 1990, 95. [Google Scholar] [CrossRef]
- Dierking, W.; Dall, J. Sea-Ice Deformation State From Synthetic Aperture Radar Imagery—Part I: Comparison of C- and L-Band and Different Polarization. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3610–3622. [Google Scholar] [CrossRef]
- Linow, S.; Hollands, T.; Dierking, W. An assessment of the reliability of sea-ice motion and deformation retrieval using SAR images. Ann. Glaciol. 2015, 56, 229–234. [Google Scholar] [CrossRef]
- Pedersen, L.T.; Saldo, R.; Fenger-Nielsen, R. Sentinel-1 results: Sea ice operational monitoring. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015. [Google Scholar]
- Li, S.; Cheng, Z.; Weeks, W.F. A grid-based algorithm for the extraction of intermediate-scale sea-ice deformation descriptors from SAR ice motion products. Int. J. Remote Sens. 1995, 16, 3267–3286. [Google Scholar]
- Thomas, M.; Geiger, C.A.; Kambhamettu, C. High resolution (400 m) motion characterization of sea ice using ERS-1 SAR imagery. Cold Reg. Sci. Technol. 2008, 52, 207–223. [Google Scholar] [CrossRef]
- Stern, H.L.; Moritz, R.E. Sea ice kinematics and surface properties from RADARSAT synthetic aperture radar during the SHEBA drift. J. Geophys. Res. 2002, 107. [Google Scholar] [CrossRef]
- Muckenhuber, S.; Korosov, A.A.; Sandven, S. Open-source feature-tracking algorithm for sea ice drift retrieval from Sentinel-1 SAR imagery. Cryosphere 2016, 10, 913–925. [Google Scholar] [CrossRef]
- Korosov, A.; Rampal, P. A Combination of Feature Tracking and Pattern Matching with Optimal Parametrization for Sea Ice Drift Retrieval from SAR Data. Remote Sens. 2017, 9, 258. [Google Scholar] [CrossRef]
- Melling, H. Detection of features in first-year pack ice by synthetic aperture radar (SAR). Int. J. Remote Sens. 1998, 19, 1223–1249. [Google Scholar] [CrossRef]
- Vesecky, J.F.; Smith, M.P.; Samadani, R. Extraction Of Lead And Ridge Characteristics From SAR Images Of Sea Ice. IEEE Trans. Geosci. Remote Sens. 1990, 28, 740–744. [Google Scholar] [CrossRef]
- Linow, S.; Dierking, W. Object-Based Detection of Linear Kinematic Features in Sea Ice. Remote Sens. 2017, 9, 493. [Google Scholar] [CrossRef]
- Hollands, T.; Linow, S.; Dierking, W. Reliability Measures for Sea Ice Motion Retrieval From Synthetic Aperture Radar Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 67–75. [Google Scholar] [CrossRef] [Green Version]
- Thorndike, A.S.; Colony, R. Sea ice motion in response to geostrophic winds. J. Geophys. Res. 1982, 87. [Google Scholar] [CrossRef]
- Lindsay, R.W.; Stern, H.L. The RADARSAT Geophysical Processor System: Quality of Sea Ice Trajectory and Deformation Estimates. J. Atmos. Ocean. Technol. 2003, 20, 1333–1347. [Google Scholar] [CrossRef]
- Bouillon, S.; Rampal, P. On producing sea ice deformation data sets from SAR-derived sea ice motion. Cryosphere 2015, 9, 663–673. [Google Scholar] [CrossRef]
- Griebel, J.; Dierking, W. Method to Improve High-Resolution Sea Ice Drift Retrievals in the Presence of Deformation Zones. Remote Sens. 2017, 9, 718. [Google Scholar] [CrossRef]
- Muckenhuber, S.; Sandven, S. Open-source sea ice drift algorithm for Sentinel-1 SAR imagery using a combination of feature tracking and pattern matching. Cryosphere 2017, 11, 1835–1850. [Google Scholar] [CrossRef]










© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Griebel, J.; Dierking, W. Impact of Sea Ice Drift Retrieval Errors, Discretization and Grid Type on Calculations of Ice Deformation. Remote Sens. 2018, 10, 393. https://doi.org/10.3390/rs10030393
Griebel J, Dierking W. Impact of Sea Ice Drift Retrieval Errors, Discretization and Grid Type on Calculations of Ice Deformation. Remote Sensing. 2018; 10(3):393. https://doi.org/10.3390/rs10030393
Chicago/Turabian StyleGriebel, Jakob, and Wolfgang Dierking. 2018. "Impact of Sea Ice Drift Retrieval Errors, Discretization and Grid Type on Calculations of Ice Deformation" Remote Sensing 10, no. 3: 393. https://doi.org/10.3390/rs10030393
APA StyleGriebel, J., & Dierking, W. (2018). Impact of Sea Ice Drift Retrieval Errors, Discretization and Grid Type on Calculations of Ice Deformation. Remote Sensing, 10(3), 393. https://doi.org/10.3390/rs10030393