Integration of PSI, MAI, and Intensity-Based Sub-Pixel Offset Tracking Results for Landslide Monitoring with X-Band Corner Reflectors—Italian Alps (Corvara)

Abstract

This paper presents an analysis of the integration between interferometric and intensity-offset tracking-based SAR remote sensing for landslide hazard mitigation in the Italian Alps. Despite the advantages of Synthetic Aperture Radar Interferometry (InSAR) methods for quantifying landslide deformation, some limitations remain. The temporal decorrelation, the 1-D Line Of Sight (LOS) observation restriction, the high velocity rate and the multi-directional movement properties make it difficult to monitor accurately complex landslides in areas covered by vegetation. Therefore, complementary and integrated approaches, such as offset tracking-based techniques, are needed to overcome these InSAR limitations for monitoring ground surface deformations. As sub-pixel offset tracking is highly sensitive to data spatial resolution, the latest generations of SAR sensors, such as TerraSAR-X and COSMO-SkyMed, open interesting perspective for a more accurate hazard assessment. In this paper, we consider high-resolution X-band data acquired by the COSMO-SkyMed (CSK) constellation for Permanent Scatterers Interferometry (PSI), Multi-Aperture Interferometry (MAI) and offset tracking processing. We analyze the offset tracking techniques considering area and feature-based matching algorithms to evaluate their applicability to CSK data by improving sub-pixel offset estimations. To this end, PSI and MAI are used for extracting LOS and azimuthal displacement components. Then, four well-known area-based and five feature-based matching algorithms (taken from computer vision) are applied to 16 X-band corner reflectors. Results show that offset estimation accuracy can be considerably improved up to less than 3% of the pixel size using the combination of the different feature-based detectors and descriptors. A sensitivity analysis of these techniques applied to CSK data to monitor complex landslides in the Italian Alps provides indications on advantages and disadvantages of each of them.

1. Introduction

Mountainous areas are recurrently affected by active instability processes, such as debris flows or landslides that can induce damages and casualties. To reduce the risks, a careful assessment and monitoring of slope deformations is required. Over the past two decades, capabilities of synthetic aperture radar interferometry (InSAR) have been demonstrated to detect and quantify land surface deformations with a precision in the order of millimeters [1]. However, some limitations and challenges hinder InSAR techniques to extract surface displacements successfully. Spatio-temporal decorrelation [2] (due to long perpendicular and temporal baselines between SAR acquisitions) and atmospheric delay [3] are two main limiting factors. Permanent Scatterer Interferometry (PSI) [4], Stanford Method for Persistent Scatterers (StaMPS) [5], Spatio-temporal Unwrapping Network (STUN) [6], Small Baseline Subsets (SBAS) [7], and Enhanced Small BAseline Subset (ESBAS) [8] have been proposed to overcome or mitigate those limitations in specific conditions.

Generally, the use of InSAR techniques in natural terrains encounters more challenges than in urban areas. Low coherence (e.g., vegetated areas) and non-steady deformation processes (e.g., complex landslide type [9]) are two main problems to retrieve accurate phase deformation using InSAR. Spatio-temporal decorrelation problems could be mitigated by employing small temporal and perpendicular baseline data set [7] and non-linearity of movements can be taken into account by applying some filter-based approaches [5]. For enabling InSAR to retrieve phase information in areas where the number of dominant scatterers is limited, several Distributed Scatterer (DS) algorithms have been developed in DS interferometry. SqueeSAR [10], SBAS, CRLB [11], CAESAR [12], virtual [13] and sequential estimator [14] are the most frequently used algorithms for DS interferometry.

One of the significant limitations of the InSAR-based technique is that the extraction of displacement components is only limited to the LOS direction. Long-track Deformation Extraction Methods (ADEM) are widely used to take into account the azimuth movement caused by earthquakes [15], landslides [16] and glaciers [17]. ADEM are classified into two main categories: (i) Split-bandwidth-based methods including Spectral Diversity (SD) and Multi-Aperture Interferometry (MAI); and (ii) offset tracking--based methods. Spectral diversity was first proposed to retrieve absolute phase [18] and then to co-register SAR pairs in the range and azimuth directions [19].

MAI technique, considered as a version of SD in azimuth, operates on the split-beam of InSAR using band pass filters into the forward- and backward-looking interferograms. It was developed for long-track deformation retrieval [20]. Since the forward- and backward-looking interferograms are geometrically symmetric, the range and troposphere components will nearly appear the same. As a result, the tropospheric phase contribution can be removed from the interferograms. In addition, phase distortions from the earth-flat and topographic effects resulting from MAI can be successfully removed [21].

Offset tracking-based methods (in the InSAR domain) are generally classified into (i) Coherent Cross Correlation (CCC), known as coherent speckle tracking; and (ii) Incoherent Cross Correlation (ICC), known as feature or pixel tracking. CCC relies on using the complex image patches and can be applied to coherent data even without any tangible and traceable scatterer. It uses cross-correlation operation as an optimum (maximum-likelihood) estimator (MLE) for offset determination of partially correlated circular Gaussian signals and some systematic (non-noise) phase differences such as topographic and flat-earth fringes [22]. CCC operates on the formation of small interferograms involving some changes in range and azimuth, the offsets is specified by detecting the peak average coherence [23]. Contrary to CCC, ICC only relies on amplitude information of image patches and attempts to find offset between traceable features (e.g., lines and rocks). It uses cross-correlation of intensity of SLC data and finds the peak location to estimate offset. If mean coherence values are high, ICC (using complex cross-correlation) is preferred, whereas CCC should be preferred if the data has low mean coherence values (using intensity cross-correlation).

Template matching algorithms are widely used for image registration and feature matching. Generally, template matching algorithms can be classified into three groups [24]: (i) featured-based algorithms that are well suited to extract the features using their spatial relations or descriptors; (ii) patch or area-based algorithms that consider the intensity of the pixel values obtained after cross-correlation-based similarity; and (iii) optical-flow or motion tracking algorithms. The first group is mainly appropriate to match structural information (i.e., features), the second one fits for intensity information and the third one is based on the relation between photometric correspondence vectors and spatiotemporal derivatives of luminance in an image sequence [25].

Feature matching enables finding correspondences between two images based on the local interest points. It plays a key role in computer vision applications such as motion estimation, image registration, object detection and tracking. Feature-based matching procedures rely on local feature detection (mainly based on gradient or intensity variation) and corresponding feature descriptors (local image gradient). The local features are usually blobs, corners or edge pixels that are extracted by an appropriate feature detection algorithm. Efficiently matching features across images is the core of feature-based algorithms in computer vison. Repeatability, distinctiveness and localization of features are the three main characteristics of a good local feature under varying imaging condition and in the presence of noise [26]. Localization refers to how well a detector can locate the exact position of features. Binary Robust Invariant Scalable Keypoints (BRISK) [27], Minimum eigenvalue algorithm (MEIGEN) [28], Harris [29], Features from Accelerated Segment Test (FAST) [30] and Fast Retina Keypoint (FREAK) are often used as corner-based feature detection functions and descriptors. Speeded Up Robust Features (SUR) [31] and Scale Invariant Feature Transform (SIFT) [32] are the most significant blob-based features descriptors in computer vision field. The descriptors of the corner-based features are mainly based on pairs of local intensity differences (e.g., BRISK) while the descriptors of the blob-based features (e.g., SURF and SIFT) are based on local gradient. The use of computer vision-based algorithms has not been widely investigated with SAR data except for the task of image registration [33,34].

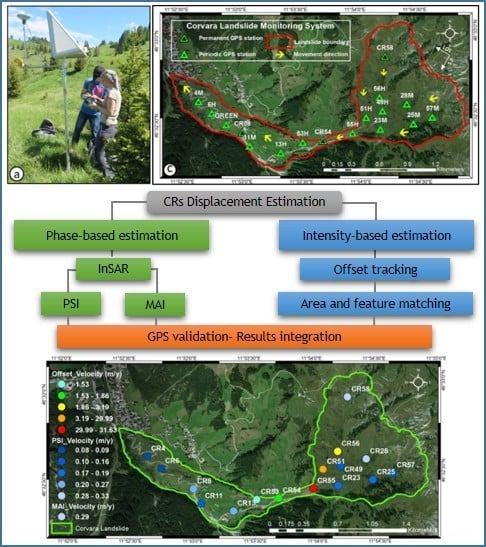
This research aims to improve the accuracy of offset estimation using computer vision techniques, and integrate the PSI, MAI, and offset tracking results to monitor a complex and vegetated landslide through X-band CRs. This allows us to overcome or mitigate the limitations of some methods. PSI is limited only to 1D LOS displacement detection and an upper limit for velocity estimation. Non-LOS displacements are not also retrievable by PSI, in such case; MAI could be considered as an alternative technique to overcome this limitation. High movement rate leads to phase aliasing in the CCC-based methods and dependency of offset estimation accuracy on data pixel size and changes in the features (e.g., geometrical distortions) are the main constraints of the ICC-based methods. Low coherence problem in vegetated areas, leading to phase unwrapping difficulty, can be tackled by using artificial CR.

The paper initiates with a brief presentation of the test site, the equipment installed and the datasets, as well as some metrics for quality assessment. The method section illustrates the techniques used in the study and some data processing tasks. The results of InSAR and offset tracking techniques applied to the CRs are presented in the following section. Finally, the performance assessment results, downsides and advantages of each technique are addressed in the discussion and conclusion sections.

2. Case Study and Dataset

2.1. Corvara Landslide

The case study is the active Corvara landslide, located in the Autonomous Province of Bolzano-South Tyrol, in the Italian Alps. It is described as a slow-moving complex earth slide-earth flow with annual displacement rates of up to 20 m [35,36] (see Figure 1c,d). The ongoing slope deformation is in the order of a few cm/year in the toe zone, and up to tens of meters per year in the most active track and source zones. Since the Corvara is among the most popular tourist attractions in the Italian Alps, the area has undergone an intense tourist development. The urban settlement has progressively increased since the late 1960s, and a dense network of facilities now serves most of the slopes. This development has significantly increased both the wealth of the area and risk to slope failures [37]. This landslide frequently causes damages to the national road SS 244, the ski infrastructures, and the nearby golf course.

The landslide behavior is characterized such as: retrogressive at the crown and flanks of the source areas; slightly enlarging at the sides of the accumulation area; slightly advancing at the turn of the landslide into the main valley; and potentially advancing at the toe [38]. The Corvara landslide has been monitored for several years with different close and far range imagery techniques such as Unmanned Aerial Vehicle (UAVs) [39], SAR data [36] and by multi-sensors data integration [40].

2.2. Artificial Corner Reflectors

In 2013, 16 Corner Reflectors (CR) specifically designed for X-band were installed on the landslide and used as reference points for InSAR and sub-pixel offset tracking. Each CR was equipped with an antenna stand with a GPS station to take monthly (Figure 1a) and hourly (Figure 2b) 3D measurements. From the CRs distribution perspective over the landslide, due to the limitation in the number of the available CRs, the priority was dedicated to the active and semi-active part of the landslide with the movement directions aligned to LOS. Thereby, it was avoided installing the CRs on a landslide part where was not regarded as an active area (according to the GPS observations) with a non-LOS movement (e.g., surrounding CR58).

GPS measurements and SAR results show different motion behaviors in terms of direction and velocity rate. The PSI technique was not able to track the high velocity rate CRs and was not considered in past processing [36]. In this work, we analyze two different motion categories (i.e., high and low velocity rates) both in LOS and non-LOS directions. If the displacement of a CR is higher than 0.5 m (within the data time span), it is of “high velocity rate”, while CR displacements less than 0.5 m are of “low velocity rate” (see

Table 1. High and low velocity rate CRs including both LOS and non-LOS directions.

Velocity Rate Type	Displacement Direction	CR No.	Magnitude of Displacement	Azimuth of Displacement
High velocity rate CRs	LOS direction	CR53	1.69 m	272°
		CR54	3.41 m	284°
	Non-LOS direction	CR51	39.95 m	171°
		CR55	46.17 m	250°
		CR56	3.57 m	167°
Low velocity rate CRs	LOS direction	CR4	12.5 cm	305°
		CR6	13.3 cm	303°
		CR8	32 cm	283°
		CR11	20.7 cm	298°
		CR13	39.1 cm	270°
		CR23	22.7 cm	260°
		CR25	20.1 cm	260°
		CR57	18.3 cm	265°
		CR28	39.1 cm	260°
		CR49	20.3 cm	265°
	Non-LOS direction	CR58	34 cm	177°

). If the azimuth displacement of a CR derived by GPS locates within the ±25° of the Azimuth LOS (ALOS) of the satellite (i.e., 280°), it is placed into the sub-group of “LOS direction”; otherwise it is labeled as non-LOS direction category. Table 1 shows the GPS measurements of 16 CRs corresponding to the satellite images. The high velocity rate CRs are processed and analyzed using offset tracking-based methods, while the low velocity rate CRs with displacements in the LOS alignment are processed using InSAR-based method (i.e., PSI). Since the CR58 displacement is less than 0.5 m according to nearly the North-South direction, it is processed using the MAI. The GPS data used here as ground truth for validating the results are described in [36].

The 27 COSMO-SkyMed StripMap (HIMAGE) data selected are characterized by a 1.56 m × 1.94 m range-azimuth pixel spacing in the descending orbit and cover the period of 464 days (i.e., between 5 April 2014 and 10 August 2015). Two DEMs were available for the Corvara area: (i) SRTM DEM (30 m) in 2000; and (ii) laser airborne DEM (2.5 m) acquired in 2006 by the autonomous Province of Bolzano. The airborne DEM was used in the InSAR processing, because it is more recent and has a finer resolution than SRTM DEM.

3. Methods

To estimate the CRs displacements several considerations must be considered in the InSAR processing. To have a reliable phase unwrapping, the unmolded phase such as atmospheric contribution must be smaller than 0.6 rad, meaning that PS pixels density must be more than 3–4 per km², for common atmospheric conditions [41]. To take into account this PS range constraint, especially for vegetated landslides, artificial corner reflectors can be used as PSs to fill the gap between the PSs network. In addition to the above-mentioned limitations, the deformation phase cannot be retrieved unambiguously when the displacement phase between two successive acquisitions goes beyond ±π [42], which refers to the Maximum Detectable LOS Displacement (MDLD) (Equation (1)). The MDLD of each adjacent pixel in a wrapped interferogram and during the phase unwrapping cannot exceed λ/2 and λ/4 (less than 0.5 interferometric fringes per pixel), respectively (Equation (2)) [43,44]. Therefore, the maximum range of displacement rate can be theoretically defined either in terms of wavelength-revisit time or in terms of wavelength-pixel size of SAR data:

$$\Delta D_{\max }=\frac{\lambda /4}{\Delta T/365.25}\hspace{0.17em}$$

(1)

$$D_{\max }=\frac{\lambda }{2r}$$

(2)

where ΔT, λ and r indicate the time interval of two successive acquisitions, the sensor wavelength and the pixel size of the SAR image, respectively. Based on Equation (1), the theoretical MDLD rates for TerraSAR-x with revisit time of 11 days, COSMO-SkyMed with the nominal repeat cycle of 16 days and Sentinel-1A/B with revisit of 6 days are 25.7 cm/year, 17.6 cm/year and 85.2 cm/year, respectively. According to Equation (2), the MDLD for TerraSAR-X (pixel size: 1 m × 1 m with 1 look), COSMO-SkyMed (pixel size: 2 m × 2 m with 1 look) and Sentinel-1A/B (pixel size 13 m × 13 m with 1 × 4 looks) will be 1.55 × 10⁻², 7.75 × 10⁻³ and 2.1 × 10⁻³, respectively. The MDLD upper limit does not consider the noise caused by the various decorrelation sources.

3.1. Data Pre-Processing

Before starting data processing, we first performed a quality assessment analysis on the CR footprints. In fact, knowing the quality and evolution of the CR signals over the time span is useful to interpret InSAR results. Then, we prepared the data for offset tracking processing.

3.1.1. CR Response Quality Assessment

When a SAR system response to a CR is reliable and stable (intensity and phase) in the time series, the CR orientation (i.e., azimuth and elevation angles) has been properly aligned toward the satellite. The Impulse Response Function (IRF) characteristic of a received signal is a significant indicator for data quality check. If a CR has been installed optimally, the footprint of a CR on a SAR image should show a cross-like shape and its IRF should be similar to an ideal IRF (i.e., a Sinc function, see Figure 2d). Several parameters can determine the quality of the SAR response to a CR including: (i) the Peak Side Lobe Ratio (PSLR) refers to the ratio between the peak elevation of the side lobe (I_s) and the peak elevation of the main lobe (I_m); and (ii) the Integrated Side Lobe Ratio (ISLR) indicates the ratio between the power in the main lobe and the total power in all the side lobes. In Figure 2d, the area below the 3 dB intensity points in the main lobe specifies Spatial Resolution (SR) of SAR data.

Table 2. CRs impulse response changes from the first and the last acquisitions. The related IRF parameters of all CRs derived from 5 April 2014 and 8 October 2015. Backscattering (Bsc) values of the CRs were directly extracted from the center of CRs footprints on the SLC data.

CR No.	CSK-05 April 2014				CSK-08 October 2015
	Bsc	RPSLR (dB)	APSLR (dB)	ISLR (dB)	Bsc	RPSLR (dB)	APSLR (dB)	ISLR (dB)
CR4	502	−11	−11.1	0.72	743	−9.9	−10.6	1.67
CR6	473	−10.8	−9.9	0.54	654	−11.1	−10	1.55
CR8	574	−10.8	−10.2	1.4	677	−10.2	−9.9	1.52
CR11	462	−10.3	−10.8	0.39	475	−9.7	−10.7	1.51
CR13	453	−10.2	−12.2	0.47	821	−10.1	−12.1	1.44
CR23	435	−10.9	−10.2	0.46	668	−10.8	−10.1	1.57
CR25	518	−9.7	11.6	1.43	631	−10.4	−11.5	0.76
CR28	443	−9.8	−11	0.48	654	−9.7	−10.6	1.6
CR49	486	−11.2	−11.2	0.5	741	−10.2	−11.1	1.46
CR51	492	−11	−11	0.53	413	−12	−9.1	1.93
CR53	426	−10.4	−10.5	1.66	831	−10.3	−11.7	1.74
CR54	512	−10.8	−12.6	1.87	671	−11.9	−16.6	−0.52
CR55	464	−11.2	−11.5	0.51	635	−10.1	−10	1.69
CR56	499	−11.1	−10.1	1.44	580	−10.1	−11.1	1.18
CR57	525	−10.1	−11.2	1.35	600	−9.8	−10.1	1.6
CR58	476	−10.2	−11.1	0.37	746	−10.1	−10.6	1.67

lists the PSLR in range and azimuth (i.e., RPLSR and APSLR) and the ISLR for each CR extracted. As an example, we show the IRF and intensity value of CR13 providing the highest backscattering signal (see Figure 2a–c). This quality check procedure helps in understanding whether the CRs have been tilted by the landslide movement or not. If so, the CR orientation changes could considerably influence InSAR and offset tracking results.

3.1.2. Data Pre-Processing

The data pre-processing was performed in two steps to use the intensity information of CSK data for offset tracking processing. First, the data were calibrated into the sigma naught (i.e., backscatter coefficients) and then georeferenced in the UTM coordinate system. To reduce the speckle, the Anisotropic Non-Linear Diffusion (ANLD) filter was applied to both images considering Gaussian blur kernel variance equal to 0.5, anisotropy equal to 5, and step size equal to 100. Attention was paid to avoid truncating high intensity values of the image pixels to a fixed value in the calibration step. Pixels with a high sigma naught are truncated to 5 in SARscape software [45]. If that happens, the CR footprints will have several pixels with identical values (i.e., 5) that affect offset estimation at the sub-pixel level.

3.2. Methodology

In this paper, the low velocity rate CRs corresponding to displacements in the MDLD range were processed using the PSI and MAI (only CR58) techniques over the time series. The high velocity rate CRs having displacements beyond the MDLD range were processed by offset tracking-based techniques. To investigate the performance of different offset tracking techniques several matching algorithms (i.e., area and feature-based matching methods) were applied to one CSK pair according to the first and last acquisition dates. This aims to estimate the CRs offsets between these two SAR images.

The area-based matching algorithms investigated in this study are (1) the Phase Correlation (PC); (2) the Modified PC (MPC) implemented by ImGRAFT [46] and COSI-Corr [47,48], respectively; (3) the Orientation Correlation (OC) implemented by ImGRAFT and CIAS [49,50], concurrently; and (4) the NCC and Statistical Correlation (SC) implemented by CIAS and COSI-Corr. In addition, the feature-based matching algorithms taken from computer vision are as follows: (1) BRISK (FREAK as descriptor); (2) HARRIS; (3) MEIGEN; (4) FAST; (5) SURF; (6) the combination of BRISK, HARRIS and MEIGEN detectors with SURF as a descriptor. All feature-based matching algorithms were implemented in MATLAB [51]. Although OC is practically a feature-based algorithm, we put it in the area-based matching category, because it uses a correlation operator for matching and a moving window-based approach. The methodology flowchart is divided into two branches according to the landslide velocity rate and the related methods for estimating it (Figure 3).

The principle of template matching-based methods of area-based algorithms relies on a predefined template with a given window size that is moved within the search window area to find the highest similarity to match a feature. The template matching-based estimator principle is illustrated in Figure 4. In the following, the theory behind each method that used in this manuscript and some implementation details related to the data processing are briefly described.

3.3. InSAR Techniques (Phase-Based Estimation)

3.3.1. Permanent Scatterers Interferometry (PSI)

To overcome the decorrelation problem due to the vegetation observed on the Corvara landslide, the PSI technique has been applied to the installed CRs. The main goal of PSI processing is the extraction of the phase displacement component without any other residual phase components especially the noise. Figure 5 shows the SAR data pairs combination and connection graph with 27 CSK images as well as the rainfall data taken from the Piz la Ila station.

The master image is selected based on the highest stack coherence (γ^m) according to the following equation [42] adopted for the CSK to maximizes the sum correlation of all the interferograms:

$${\gamma }^m=\frac{1}{K}{\displaystyle \sum _{K=0}^{K}g\left(B_{\perp }^{k,m},\hspace{0.17em}5000\right)\times g\left(T^{k,m},\hspace{0.17em}1.5\right)\times g\left(f_{dc}^{k,m},\hspace{0.17em}1260\right)}\hspace{0.17em}$$

(3)

where

$$g\left(x,c\right)=\{\begin{array}{ll}1-\left|x\right|/c& \hfill if\left|x\right|<c\hfill \\ 0& \hfill otherwise\hfill \end{array}$$

(4)

with $B_{\perp }^{k, m}$ as perpendicular baseline between images m and k at the center of images, $T^{k,m}$ temporal baseline (in years), and $f_{dc}^{k,m}$ Doppler baseline. Since the time span of the dataset is nearly less than one and a half years, we consider 1.5 years as an upper limit for the temporal baseline. The master and slaves chosen according to Equation (3). The minimum and maximum perpendicular baselines are of 42 m and 976 m, respectively to the master image, which are smaller than the critical baseline.

The PSI processing [4] was run with the SARscape software following five steps: (1) single master connection network creation; (2) images co-registration, interferogram generation and flattening; (3) first inversion; (4) second inversion and (5) displacement geocoding. First, all slaves are co-registered to the master image with an oversampling factor of 4 in range to avoid aliasing. None of Doppler separation of each slave and master was beyond the critical $f_{dc}$, hence, no Doppler filtering was applied. Since the perpendicular baselines of all pairs are much lower than the critical baseline (45% of the critical baseline), the spatial decorrelation is very limited. No spectral filtering is applied in order to keep the data at the highest resolution possible and increasing pixel probability to be dominated by one scatterer [5]. Initial PS pixels selection was performed by using the ratio of the standard deviation to its intensity average, known as the amplitude dispersion index (D_A). In the first inversion step, the residual height and displacement velocity were obtained by considering the reliability of phase history of selected PS pixels using the linear model. The phase offset retrieved from the interferograms was removed using the highest coherent pixel selected within a predefined area (5 sqkm) as a reference point. The second inversion estimated the atmospheric phase components by using the previous model and the second linear model to fit the final displacement after removing the atmospheric phase. Low and high band pass filtering with window sizes of 1000 and 365 (days) were then applied to remove the spatial and temporal distributions of the atmospheric variations.

In the validation step, the GPS measurements have been projected into the LOS direction to be compared with PSI results. The sensitivity decomposition can be obtained using unit vector, as a function of range and azimuth changes for LOS (cross-track) [52] and along-track deformation, as follows:

$$U_{Cross\hspace{0.17em}track(LOS)}={\left[U_u,\hspace{0.17em}{U}_n,\hspace{0.17em}{U}_e\right]}^T\left[\cos \left({\theta }_{inc}\right),\hspace{0.17em}\sin \left({\theta }_{inc}\right).\sin \left({\alpha }_h\right),\hspace{0.17em}-\sin \left({\theta }_{inc}\right).\hspace{0.17em}\cos \left({\alpha }_h\right)\right]\hspace{0.17em}$$

(5)

$$U_{Along\hspace{0.17em}track}={\left[0,\hspace{0.17em}{U}_n,\hspace{0.17em}{U}_e\right]}^T\left[0,\hspace{0.17em}-\cos \left({\alpha }_h\right),\hspace{0.17em}-\sin \left({\alpha }_h\right)\right]\hspace{0.17em}$$

(6)

The sensitivity decomposition of LOS deformation obtained by substituting ${\theta }_{inc}$ and ${\alpha }_h$ in Equation (5), is $\left[0.697,-0.185, 0.692\right]{\left[U_u,U_n,U_e\right]}^T$.

3.3.2. Multi-Aperture Interferometry (MAI)

MAI is an advanced InSAR technique based on the split-beam of InSAR processing using a modification of the Doppler centroid into forward (${\phi }_f$) and backward (${\phi }_b$) looking interferograms [20]. The resultant phase difference between two SAR pairs can be used for estimating a long-track displacement. The MAI phase (Equation (7)) and its accuracy (Equation (8)) are defined as:

$${\phi }_{MAI}={\phi }_f-{\phi }_b=\frac{4\pi n}{l}\hspace{0.17em}\Delta r$$

(7)

$${\sigma }_{MAI}=\frac{4\pi n}{l}\hspace{0.17em}{\sigma }_{\Delta r}$$

(8)

where l is the length of the antenna, n is a normalized squint (fraction of the full aperture width), ${\sigma }_{\Delta r}$ and ${\sigma }_{MAI}$ are the standard deviations of the phase and displacement measurements, respectively [20,21]. Since the movement direction of the CR58 is approximately aligned to the azimuthal direction (nearly N–S) with a magnitude of about 34 cm, for reducing the computational load of the data processing, MAI was applied to half of the SAR data over the full time series. Moreover, different multi-looking factors (4 × 4, 16 × 16 and 64 × 64) and n parameters (i.e., 1/2 and 1/4) were tested.

3.4. Intensity-Based Estimation

3.4.1. Offset Tracking (Area-Based)-Frequency and Spatial Domains

Phase Correlation (PC)

Image matching can be performed in the frequency domain referring to phase correlation. Let f₁(x,y) and f₂(x,y) be two signals with the corresponding matching window of the first and second images at the time of t₁ and t₂. The offset presented (Δx and Δy) in the second image (f₂) is defined by

$$f_2\left(x,y\right)=f_1{\left(x-\Delta x,y-\Delta y\right)}_{}$$

(9)

By taking the Fourier, the normalized phase correlation (known as the cross-power spectrum) is as follows:

$$CC\left(u,v\right)=\frac{F_2\left(u,v\right)F_1{\left(u,v\right)}^{*}}{\left|F_2\left(u,v\right)F_1{\left(u,v\right)}^{*}\right|}=e^{-i\left(u\Delta x+v\Delta y\right)}$$

(10)

where F₁ and F₂ are FFT of f₁ and f₂, and * indicates the complex conjugate. Two PC versions were applied to the intensity-based SAR images: (i) the standard PC; and (ii) a modified version of PC (MPC). MPC minimizes the weighted residual matrix between the computed normalized cross-spectrum and the theoretical one to both reach more flexibility on the frequency weighting and to solve the phase wrapping ambiguity. It uses an iterative process (re-computing times of frequency mask adaptively) to increase the robustness and accuracy, and frequency masking to obtain a bias-free correlation [47]. The robustness iteration and mask threshold parameters are firstly set to 2 and 0.9, respectively. To investigate the role of the robustness iteration parameter in accuracy improvement of the offset estimation, its value is then increased to 4 by a resampling process.

Orientation Correlation (OC)

OC is a template-matching algorithm in the featured-based matching category and relies on orientation of image intensity gradients [53]. After indexing images using (x,y), where x and y are integers, two images $f_1$ and $f_2$ are matched. The Orientation Intensity Of Gradient (OIOG) of the images $f_1$ and $f_2$ are built up according to [53]:

$$f_1\left(x,y\right)=\mathrm{sgn}\left(\frac{\partial f_1\left(x,y\right)}{\partial x}+i\frac{\partial f_1\left(x,y\right)}{\partial y}\right)$$

(11)

$$\hspace{0.17em}{f}_2\left(x,y\right)=\mathrm{sgn}\left(\frac{\partial f_2\left(x,y\right)}{\partial x}+i\frac{\partial f_2\left(x,y\right)}{\partial y}\right)$$

(12)

$$\mathrm{sgn}\left(x\right)=\{\begin{array}{ll}0& if\left|x\right|=0\\ \frac{x}{\left|x\right|}& otherwise\end{array}$$

(13)

sgn(x) and i indicate the sign function and complex imaginary unit, respectively. The orientation images are then matched using inverse FFT-based correlation. Since OIOG on the images has no gradient (i.e., 0 + 0i) for uniform regions and is equal to 1, hence, OC is invariant to offset illumination changes [53].

Normalized Cross Correlation (NCC)

NCC is a robust and simple method to seek for a particular pattern that has probably been shifted in two subsequent (in time) images to find the related offset. In cross-correlation-based offset tracking, a template with the function $f_2$(x,y) and size of N_x × N_y is moved across an image with the function $f_1\left(x,y\right)$ and size of M_x × M_y by u step in x-direction and v step in y-direction pixel by pixel. All cross-correlation coefficients are stored in the correlation matrix as follows:

$$CC\left(u,v\right)=\frac{{\displaystyle {\sum }_{x,y}\left(f\left(x,y\right)-{\overline{f}}_{u,v}\right)\left(t\left(x-u,y-v\right)-\overline{t}\right)}}{\sqrt{{\displaystyle {\sum }_{x,y}{\left(f\left(x,y\right)-{\overline{f}}_{u,v}\right)}^2{\left(t\left(x-u,y-v\right)-\overline{t}\right)}^2}}}$$

(14)

where $u\in \left\{0, 1, 2, \dots , M_x-N_x\right\}, v\in \left\{0, 1, 2, \dots , M_y-N_y\right\}$, and $\overline{f}$_u,v and $\overline{t}$ indicate the average value of the search $f_1\left(x,y\right)$ and $f_2\left(x,y\right)$ template windows shifting with (u,v) steps. Computation of Equation (14), especially for a large image, is intensive and needs a calculation in order of (N_x × N_y ) × (M_x − N_x) × (M_y − N_y) [54]. For instance, the computational load for a NCC calculation with a template and search windows size of 64 × 64 and 128 × 128 pixels, respectively, is more than 10⁶ operations. NCC algorithm was applied to one SAR pair using CIAS and COSI-Corr. SC in COSI-Corr uses the statistical approach based on the cross correlation. To evaluate the effect of using different templates and search windows on the accuracy of the offset estimation, several windows were defined based on an initial guess of the CRs displacements (i.e., with 64 × 64, 32 × 32 and 16 × 16 search windows, 16 × 16 and 8 × 8 template windows and according to 2, 4 and 8 pixels during the moving window step). This procedure is used for each area-based estimator.

3.4.2. Offset Tracking (Feature-Based)—Spatial Domain

Generally, the BRISK algorithm includes three main parts: (i) sampling pattern; (ii) orientation compensation; and (iii) sampling pairs [27]. The features in BRISK are extracted in octave layers and layers in-between of the image pyramid, and then the location and the scale of each feature is acquired in the continuous domain via quadratic function fitting [27]. The BRISK descriptor uses Hamming distance instead of Euclidean distance to match features utilizing the sum of XOR operation between two binary descriptors [27]. HARRIS operates on the second moment matrix (auto-correlation matrix) to detect the features using the gradient distribution in a local vicinity of a point-like target [29]. MEIGEN is a feature detector that extracts the point feature using a measure of feature dissimilarity to quantify the changes between two images [28]. FAST detector uses comparing of pixels where those have only been located on a circle of fixed radius around the point (i.e., 16 pixels) to consider the object as a corner candidate [30]. SURF detector considers integral images for image convolutions and Fast-Hessian matrix. The SURF descriptor is based on dividing the neighborhood region of each feature into sub-square regions (i.e., 4 × 4) and then calculating the response of a 2-dimenssions Haar wavelet for each sub-region [31]. FREAK, as a binary descriptor, was also used by the BRISK detector for describing the detected BRISK-based features. FREAK is a cascade of binary strings computed by efficiently comparing image intensities over a retinal sampling pattern [55]. To utilize the high capability of SURF in localization, four corner-based detectors (i.e., BRISK, HARRIS, MEIGEN FAST) were combined with the SURF descriptor in the feature matching step. In this way, the improvement potential of the offset estimation accuracy could be investigated and compared with the previous status (i.e., the corner-based algorithms as either detector or descriptor). The set of parameters for the feature detection function were presented in

Table 3. Set of parameters used for the processing of the feature detection functions and descriptors.

Parameters	BRISK	HARRIS	MEIGEN	FAST	SURF
Minimum intensity *	0.2	-	-	-	0.2
Minimum quality	0.1	0.01	0.01	0.1	-
Gaussian filter size		5	5	-	-
Number of octaves	4	-	-	-	4
Number of scale **	-	-	-	-	4

* Minimum intensity difference between corner and surrounding region. ** Number of scale levels per octave.

.

4. Results

4.1. InSAR Results

PSI and MAI Results

The PSI accumulative displacement is represented in Figure 6. In the plots, the GPS measurements are projected to the LOS for the PSI results and to the satellite azimuth for the MAI results using Equations (5) and (6), respectively. As GPS measurements were not acquired exactly at the same time (i.e., there were few days of difference) that the CSK acquisitions, the GPS measurements were approximated by a linear curve to make them comparable with the PSI results. The goodness of fit parameter (i.e., the R-square) for each fitted line is reported in

Table 4. InSAR results summary in terms of: Amplitude Dispersion index (D_A = σ/μ), Multitemporal coherence (M_c), Total Displacement of PSI and GPS measurements (TD_PSI and TD_GPS), Std of the PSI measurements and Root Mean Square Error (RMSE_TD) values between GPS and PSI and MAI measurements. V_R refers to the percentage ratio of GPS and PSI velocities and R² indicates R-squared values of the linear curve fitting to the GPS measurements (in Figure 6).

CR No.	Da	Mc	Azimuth.	TDPSI (cm)	TDGPS (cm)	StdPSI (cm)	RMSEd (cm)	VPSI (cm/year)	VGPS (cm/year)	R2 (GPS)
4	0.12	0.61	305°	12.4	12.5	3.87	1.04	9.20	9.58	0.98
6	0.06	0.62	303°	11.8	13.3	3.75	1.62	8.83	10.77	0.97
8	0.13	0.56	283°	31.7	32	2.15	0.85	23.55	23.89	0.99
11	0.08	0.62	298°	20	20.7	2.20	0.50	15.45	15.9	0.96
13	0.19	0.57	270°	37.5	39.1	4.00	4.07	27.84	29.97	0.98
28	0.12	0.53	260°	44.8	39.1	6.00	2.68	28	30.03	0.96
49	0.21	0.51	265°	21.2	20.3	6.68	1.83	16.46	15.67	0.97
25	0.12	0.56	265°	20.3	20.1	6.23	2.47	17.74	16.21	0.96
23	0.19	0.52	260°	20.9	22.7	6.66	4.28	19.14	17.45	0.96
57	0.11	0.58	265°	19.5	18.3	5.99	3.16	14.50	14.15	0.89
58 *	0.14	-	177°	29	34	4.1	3.2	19	23.1	-

* The displacement of CR58 is derived by MAI. The MAI and GPS measurements for CR58 are in the satellite azimuth geometry.

. Figure 6 shows that the deviation of the PSI results from the GPS line varies for each CR. CR6, 23 and 57 present a variable agreement, CR4, 13, 28, 25 and 49 have a moderate agreement, and CR8 and 11 have a good agreement with the GPS measurements.

The PSI and MAI results (including comparison of the velocity rates between PS, MAI and GPS, and accuracy assessment) are presented in Table 4. The Multi-temporal coherence (M_c) parameter shows how well a CR displacement trend fits with the linear model that was already selected for PSI processing. More M_c is close to 1 value, more the related PSI results fit the linear model. According to Table 4, CR8 and 11 presented the lowest Standard deviation (Std) and RMSE among the other CRs, and CR28, 49, 25, 23 and 57 (which are in the most active part of the landslide with different displacements in azimuth with respect to the LOS) presented the highest Std and RMS. The CR6 and CR28 provided the minimum (8 cm/year) and maximum (28 cm/year) velocity rates, respectively. The displacement of CR58 was the only one derived by MAI and the displacements of the high velocity rate CRs cannot be estimated by MAI due to the MDLD restriction

4.2. Offset Tracking Results

4.2.1. Area-Based Matching Results

The displacements of the high velocity rate CRs were extracted by the offset tracking estimators. The displacements maps and the corresponding SNR are shown in Figure 7. The CRs offsets extracted by each estimator at the center of each CRs footprint (red points). The 2-dimension offset (dx and dy) and SNR values for each CRs are provided in

Table 5. Comparison of dx and dy offsets (in meter) with the related SNR for four area-based offset tracking and OC algorithms.

CR No.	GPS		SC			NCC			MPC			OC			PC
	dx	dy	dx	dy	SNR	dx	dy	SNR	dx	dy	SNR	dx	dy	SNR	dx	dy	SNR
53	1.6	0.3	0.3	0.2	0.89	0.2	0.3	0.96	0.5	0.06	0.99	0.5	1.2	0.79	2.06	0.16	0.47
54	3.2	1.1	2.4	1.3	0.87	1.2	2.7	0.92	2.4	0.6	0.99	2.2	1.2	0.77	3.02	2.8	0.41
56	0.7	3.4	2.2	3.7	0.92	2.2	3.7	0.98	2.1	3.7	0.98	2.2	3.7	0.96	1.9	4	0.7
51	6.1	39.4	7	39.3	0.78	-	-	-	6.8	39.5	0.78	7	39.2	7.9	6.12	39.9	0.5
55	40	14	40.7	14.8	0.8	40.7	14.7	0.85	40.7	14.4	0.97	40.2	14.2	0.81	39.7	15.8	0.41
58	0.016	0.35	0.45	0.12	0.9	0.5	0.25	0.98	0.43	0.06	0.99	0.25	0	0.9	0.09	0.19	0.8

.

According to Table 5, the best-offset estimations are obtained by the PC (for CR53, 51 and 58) and the OC (for CR54, 56 and 55) with respect to the GPS measurements. As OC results derived from CIAS and ImGRAFT are similar, only OC result obtained by ImGRAFT are presented.

The accuracy assessment of the offset tracking results is given in

Table 6. Accuracy of the extracted offsets (i.e., %P_x and %P_y) in terms of the pixel size percentage. SP_xy is an indicator showing the total accuracy for each CR.

CR No.	SC			NCC			MPC			OC			PC
	%Px	%Py	SPxy	%Px	%Py	SPxy	%Px	%Py	SPxy	%Px	%Px	SPxy	%Px	%Px	SPxy
53	50	5	55	70	0	70	55	12	67	55	45	100	23	7	30
54	40	95	135	95	80	175	40	25	65	50	5	55	10	85	95
56	75	15	90	75	15	90	70	15	85	65	12	77	60	30	90
51	45	5	50	-	-	-	35	5	40	45	10	55	1	31	32
55	35	40	75	35	35	70	35	20	55	10	10	20	14	90	104

. The error of the extracted offsets in x (i.e., %P_x = (dx_GPS − dx_estimator)/2 × 100) and y (i.e., %P_y = (dy_GPS − dy_estimator)/2 × 100) directions are given in terms of the percentage of the pixel size of the image (i.e., 2 m). For instance, %P_x of %0, %50 and %100 indicate a correct estimation, one and a half pixel and one pixel size. The summation of x-y accuracy (i.e., SP_xy = %P_x + %P_y) is an index that shows the performance of each estimator with respect to its counterparts. A lower index (i.e., lower error) means that a higher accuracy has been achieved by the related estimator in x and y directions.

The accuracy obtained by the area-based matching (Table 6) shows that all estimators can extract a sub-pixel accuracy in the estimation of displacement in the x and y directions in most cases. Based on SP_xy index, OC and PC presented the absolute highest accuracy among other estimators (i.e., OC for CR54, CR56, CR55, and PC for CR53 and CR51). Although the PC showed the highest accuracy for CR53 and CR51, MPC has generally better performance than PC for all CRs. Using a higher robustness iteration parameter (i.e., 4) and applying the resampling process, simultaneously, we observed a small increase of accuracy in the MPC results. Both the NCC-based estimators (i.e., SC by COSI-Corr and NCC by CIAS) yielded similar results with a relative superiority of SC. Since both use the NCC function to estimate the offset, these results suggest differences in their algorithm implementation. For the CR51, NCC was not able to estimate the displacement.

4.2.2. Feature-Based Matching Results

The results of the CRs offsets derived by the feature-based matching algorithms with respect to the GPS measurements are presented in

Table 7. The dx and dy offsets (in meter) for four corner-based feature matching algorithms and the combination of BRISK with FREAK, and HARRIS, MEIGEN and FAST with SURF.

CR No.	GPS		BRISK		HARRIS		MEIGEN		FAST		BRISK_S		HARRIS_S		MEIGEN_S
	dx	dy	dx	dy	dx	dy	dx	dy	dx	dy	dx	dy	dx	dy	dx	dy
53	1.6	0.3	1.3	0.4	0.9	0	1.14	0.2	-	-	3.06	0.4	0.9	0	1.14	0.2
54	3.2	1.1	2.4	2.8	2.6	1.4	2.4	1.4	6	6	4.8	1.6	2.6	1.4	2.4	1.4
56	0.7	3.4	2.0	3.6	2.4	3.8	2.2	3.6	0	4	0.8	3.6	2.4	3.8	2.2	3.6
51	6.1	39.4	7.4	38.0	7	39.4	7	39.4	-	-	9	37	7	39.4	7	39.4
55	40	14	37.4	14.6	41	14.8	41	14.8	36	14	37.4	14.6	41	14.8	41	14.8
58	0.016	0.35	0.4	0.9	0.8	0	0.8	0.04	-	-	0.4	0.86	0.8	0	0.8	0.04

. The best-offset estimations are obtained by: the BRISK for CR53, the HARRIS for CR54, the BRISK_S for CR54, the MEIGEN and MEIGEN_S for CR58, and, the HARRIS and MEIGEN (with SURF descriptor as well) for CR51 and 55 (see Table 7).

The corner-based detectors were completely able to find all CRs on the images (except using FAST for CR53, 51 and 58). After running the corner and blob-based algorithms on the SAR data, all corner-based detectors (except FAST for CR53, 51 and 58) could detect all the CRs positions properly (e.g., BRISK in Figure 8a), whereas the blob-based detector (i.e., SURF) was not able to detect none of the CRs positions (Figure 8b).

After finding the desired features (CRs), they have matched by the relevent descripors. For example, the CRs extrected by BRISK detector in Figure 8a have been matched using the FREAK descriptor to the pair of SAR data (see Figure 9). Random sample consensus (RANSAC) [56] was used to only keep the inlier matched connections and remove the outliers when the features matched wrongly.

The offset accuracies of the feature-based algorithms are shown in

Table 8. Extracted offsets accuracy (i.e., %P_x and %P_y) in terms of pixel size percentage. SP_xy is an indicator showing the total accuracy for each CR.

CR No.	BRISK			HARRIS			MEIGEN			FAST			BRISK_S			HARRIS_S			MEIGEN_S
	%Px	%Py	SPxy	%Px	%Py	SPxy	%Px	%Py	SPxy	%Px	%Px	SPxy	%Px	%Px	SPxy	%Px	%Px	SPxy	%Px	%Px	SPxy
53	15	4	19	35	16	51	23	6	29	-	-	-	73	4	77	35	16	51	23	6	29
54	40	82	122	30	12	42	40	12	52	140	242	382	80	22	102	30	12	42	40	12	52
56	65	6	71	85	16	101	75	6	81	35	26	61	5	6	11	85	16	101	75	6	81
51	65	70	135	44	0	44	44	0	44	-	-	-	145	120	265	44	0	44	45	0	44
55	130	30	160	50	40	90	50	40	90	200	0	200	130	30	160	50	40	90	50	40	90

. Based on SP_xy index, BRISK, HARRIS, MEIGEN and their combination with SURF presented the absolute highest accuracy. HARRIS, BRISK and MEIGEN generally presented more accurate results, respectively, and the FAST showed the worst accuracy.

5. Discussion

5.1. InSAR

5.1.1. Non-Linearity Effect in PSI

According to the CR quality assessment results, we observed that the footprints of the CR13 (Figure 2b) and CR58 (Figure 4c) do not correspond to a cross-like shape, meaning that their IRFs are not the ideal ones (as presented in Figure 2d). A comparison of the RPSLR, APSLR and ISLR parameters between the first and last acquisitions (Table 2) clearly shows variations of the values. These changes indicate that CRs did not keep the optimal orientation during the data acquisition time span. This problem has probably occurred due to the landslide movement tilting the CRs. The tilts led to un-correlated signal in the clutter region (i.e., the grass surrounding the CRs) and induced a phase error. The probability density function (pdf) (Equation (15)) of phase error (${\phi }_e$) (Equation (16)) for a Point Scatterer (PS) shows that the amplitude of the phase error depends on the Signal to Clutter Ratio (SCR) (Equation (17)) [57]:

$$pdf\left(\phi \right)=\frac{\sqrt{SCR}\hspace{0.17em}.\hspace{0.17em}\left|\mathrm{Cos}\left(\phi \right)\right|}{\sqrt{\pi }}.\hspace{0.17em}{e}^{SCR.{\mathrm{Sin}}^2\left(\phi \right)}\hspace{0.17em}$$

(15)

$$\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\phi }_e=\frac{1}{\sqrt{2.SCR}}$$

(16)

$$SCR=\frac{{\sigma }_T}{\langle {\sigma }_C\rangle }=\frac{{\sigma }_T}{\langle {\sigma }^{\circ }\rangle A}$$

(17)

where ${\sigma }_T$, ${\sigma }_C$, ${\sigma }^{°}$ and A indicate SCR of PS, average of SCR clutter, sigma naught and surface around the PS, respectively [58]. Equations (15) and (16) imply that by increasing the SCR the width of the pdf of the phase error narrows and the phase error decreases.

Some considerations are also inferred by investigating the PSI results accuracy assessment of each CR (Table 4). $D_A$ of all CRs have values smaller than 0.25 leading to a high coherence of the SAR signals that indicates that CR backscattering values allow them to be considered as PS despite the accrued tilting. ${\mathrm{M}}_{\mathrm{c}}$ values vary between 0.51 (the lowest for CR57) and 0.62 (the highest for the CR6 and CR11), which implies a deviation of CRs motion type from the linear behavior. The GPS measurements showed a not-steady status and some irregular patterns (i.e., sudden vertical changes for some given time) in the CRs movements. The vertical changes of CR6 and CR28 (measured by GPS) are here represented as examples of non-linear and linear CRs behaviors (see Figure 10). The effect of this non-linearity can be observed in PSI results. If we compare the cumulative displacements of CR28 with CR6 (Figure 6), CR28 shows clearly a better agreement than CR6 with the GPS line.

These sudden and irregular changes are mainly related to the landslide movement itself probably trigged by specific meteorological conditions. Since the conventional PSI technique is based on a predefined linear model, the effect of non-linearity appears as a bias in the precision assessment step (e.g., high RMSE value). Different quadratic, cubic and stepwise models can be used as pre-defined models to mitigate the effect of non-linearity. However, adapting a function that perfectly represents the motion type of natural phenomena (e.g., landslide) is not straightforward, due to their unpredictability and complexity. Therefore, non-predefined model-based techniques, which relies on spatial-correlation filtering, turn out more appropriate for monitoring complex natural terrain [5].

While deformation information derived by the PSI technique is limited to LOS direction, an increase of the uncertainty is expected for non-LOS displacements. However, a meaningful trend is generally observed by assessing the Std of PSI results and azimuth displacements of each CR (Table 4). The Std and RMSE decrease at the CRs with the displacement azimuth close to LOS in comparison to other CRs. Since the azimuth displacement of CR8 (i.e., 283°) is very close to the azimuth of LOS (i.e., 280°), we assume that the Std of its measurement equals LOS precision (corresponding to 3.17 cm displacement). Therefore, the precision of the vertical and horizontal displacements was calculated using Equation (5) based on this assumption (Figure 11). The Std values increase (i.e., decrease in precision) by getting away from the LOS direction shown on the circle in Figure 11c.

Another key factor that could potentially lead to a bias in the GPS measurements, which in turn increases Std values in Table 4 is CR tilting. Since the phase center variation (PCV) of GPS antenna is computed in the horizontal position, any slight changes (e.g., tilting) in the antenna statues causes the PCV estimation are not valid anymore and the measurements are biased corresponding to the degree of the antenna tilting.

With respect to the InSAR-PSI results, a lower LOS Std for C-band CR displacement (i.e., 5 mm) has been reported with a related sensitivity analysis for urban areas [59] [60]. Several main reasons can justify the higher Std values of our results including lack of an optimal orientation of the CRs and the errors propagated in the measurement caused by the non-linearity behavior of CR motion type installed in the natural terrain. In summary, many error sources can contribute to PSI measurements leading to the increase of Std and RMSE. They can be categorized into three main categories: (i) CR-related error sources such as manufacturing, optimal size, and CR orientation; (ii) GPS measurement error (in the PCV computation due to the CRs tilting); (iii) performance of the used InSAR algorithm for the intended application (i.e., predefined model-based or non-model-based); and (iv) other external noise (e.g., atmosphere).

5.1.2. MAI Challenges and Limitations

The precision of the MAI phase is a function of n (normalized squint) in Equation (8) and MAI phase is determined by the following equation [61]:

$${\sigma }_{MAI}\approx \frac{1}{\sqrt{2N_{L.MAI}}}\frac{\sqrt{1-{\gamma }^2}}{\gamma }$$

(18)

$$\gamma =\frac{{\gamma }_f+{\gamma }_b}{2}$$

(19)

$$N_{L.MAI}=N_a.N_r.\left(B_s.PRF\right).\left(B_c.f_s\right).W_s$$

(20)

where N_l and $\gamma$ refer to the effective number of looks and total correlation (forward ${\gamma }_f$ and backward ${\gamma }_b$), respectively. The N_L.MAI is determined by the system parameters: the multi-looking factor in azimuth (N_a) and range (N_r), the chirp bandwidth (B_c), the sub-aperture Doppler bandwidth (B_s), the sampling frequency (f_s), the pulse repetition frequency (PRF) and the noise reduction factor by an adaptive filtering (W_s) [61].

According to Equations (8) and (18), the MAI phase precision can be improved by increasing n and N_L.MAI When we increased N_a and N_r (i.e., 4 × 4, 8 × 8 and 16 × 16) the coherence considerably deceased. As CRs represent clusters of coherent pixel, surrounded by low coherence ones (i.e., vegetation), increasing the multi-looking factor spatially averages the coherence values decreasing the coherence. Therefore, this limitation does not make it possible to increase the MAI phase precision by increasing the multi-looking factor. Regarding increasing the “n” parameter, an increase of “n” did not improve the MAI results in terms of displacement precision. Since the satellite observes the CR as a point-like target, at least within a quite wide range of angles, it does not matter how much the separation width of the aperture is, in any case the CR will be viewed by satellite as a point target depart from any change in the squint angle. In the high velocity rate CRs category, only the CR58 displacement (about 34 cm) was in the range of MAI maximum detectable displacement and other CRs experienced a displacement of more than one meter in the time span. As the CR58 displacement azimuth (i.e., 177°) was nearly along the satellite azimuth (i.e., 190°), the displacement accuracy derived by the MAI technique provided higher accuracy (i.e., 2.5%-pixel size) than with offset tracking techniques (see

Table 9. The offsets and error %P (i.e., P = (D_gps − D_est)/2 × 100) for CR58 (unit in meter). All the offsets obtained by the estimators and GPS measurements were projected to the satellite azimuth direction using Equation (6).

		InSAR	Area-Based Matching					Feature-Based Matching
CR No.	GPS	MAI	SC	NCC	MPC	OC	PC	BRISK	HARRIS	MEIGEN	FAST	BRISK_S	HARRIS_S	MEIGEN_S
58	0.34	0.29	0.19	0.2	0.13	0.043	0.2	0.95	0.13	0.17	-	0.91	0.13	0.17
%P		2.5	7.5	7	10.5	14.8	7	30.5	10.5	8.5	-	28.5	10.5	8.5

).

Although MAI measurement precision up to approximately 1% of the azimuth resolution has been reported [61] in a high coherent region and applying a high multi-looking factor, the restriction of multi-looking factor (leading to a decrease in coherency) does not improve the precision for the CR displacement. Despite this limitation, the estimated displacement using the MAI technique outperformed the offset-based techniques in the azimuth direction.

A comparison of ADEM precision (i.e., CCC, ICC, SD) in SAR domain is provided in the following. The precision equations of the coherent (CCC) [22] and incoherent (ICC) [62] and spectral diversity (SD) [63] are as follows:

$${\sigma }_{CCC}=\sqrt{\frac{3}{2N}}\hspace{0.17em}\frac{\sqrt{1-{\gamma }^2}}{\pi \gamma }$$

(21)

$${\sigma }_{ICC}=\sqrt{\frac{3}{10N}}\hspace{0.17em}\frac{\sqrt{2+5{\gamma }^2-7{\gamma }^4}}{\pi {\gamma }^2}$$

(22)

$${\sigma }_{SD}=\frac{1}{2\sqrt{2}}\frac{B_c}{B_c-B_s}\sqrt{\frac{B_c}{b_s}}\frac{1}{\sqrt{N}}\frac{\sqrt{1-{\gamma }^2}}{\pi \gamma }$$

(23)

where $\gamma$, N, B_c and B_s refers to coherence, independent samples, bandwidth, and sub-bandwidth, respectively. Therefore, by assuming γ→1, the variance comparison ratio shows that of ${\sigma }_{ICC}^2$ is 1.8 times more than ${\sigma }_{CCC}^2 \left({\sigma }_{ICC}^2/{\sigma }_{CCC}^2=9/5=1.8\right)$ [62]. It means that ICC will provide a better precision than CCC when we have good coherence. In the same way, the accuracy ratio (${\sigma }_{SD}^2/{\sigma }_{CCC}^2)$ of SD and CCC is equal to $1.06$ and $1.15$, respectively, for the bandwidth gap of 1/3 and 1/5 while measured $1.6$ that means that SD outperforms ICC and both are superior to CCC [17].

5.2. Offset Tracking

5.2.1. Potentials of the Area-Based Matching Algorithms

To evaluate the performance of each estimators in details, the evolution of the footprint of each CR and its pixel values must be investigated. For instance, the footprint of CR53 and CR55 (with related pixel values) show the slight and drastic pixel values changes between the first and last data acquisition, respectively (Figure 12). According to the PSLR and ISLR parameters of the CRs (Table 2), the tilts on the CRs triggered by the landslide movement caused some changes in those parameters. The CRs tilting have modified data pixel values leading difficulties for similarity-based or variant-sensitive estimators to find the exact position of the signal peak for an accurate offset estimation (see Figure 12).

The function behavior of each estimator of the CR footprint could be an appropriate indicator to understand why some estimators provide more precise results than others for a given CR. Figure 13 reports three functions of the used estimators from three template matching categories (i.e., phase-based (PC), feature-based (OC) and cross correlation-based (NCC)) depicted. The NCC response to the CRs corresponding to stable pixels values (i.e., CR53 and CR54) between two data acquisitions is nearly flat, whereas those with highly changing pixel values due to tilting (i.e., CR51 and CR55) have uneven or semi-flat surface. PC response provides a single sharp peak for the nearly fixed CRs (i.e., CR53 and CR54) and multiple sharp peaks for the tilted CRs (i.e., CR51 and CR55). OC, as a feature-based method, seeks for a distinctive feature (the CRs footprint) using a pre-defined descriptor (i.e., OIOG). The results show that PC and OC outperform NCC and OC is relatively superior to PC.

Despite reliability and simplicity of CC-based methods, such as Normalized CC (NCC), several downsides have been reported [64,65] . In this study, we noticed that the NCC accuracy of offset estimation is sensitive to noise and limited to the data pixel size. In addition, changing scale, rotation or shearing of image features lead to decrease the correlation coefficient. Some drawbacks of CC-based matching related to the geometrical changes could also be mitigated using the generalized versions of CC-based methods [66,67,68].

5.2.2. Potential of the Feature-Based Matching Algorithms

For CR53, CR54 and CR56 that are slightly tilted (small changes in pixel values and shape) comparing to CR51 and CR55 (drastic changes in pixel values and shape) by the landslide movement, feature-based matching results outperformed the area-based ones. This means that the feature-based matching algorithms (as invariant detectors/descriptors to feature deformation) managed to cope with some degrees of the distortion caused by CR tilting. While in the case of drastic changes in pixel values (e.g., CR51 and CR55), they were not able to remain invariant to the pixel value variations.

The comparison of the area and feature-based results in

Table 10. SP_xy index comparison between area and feature-based matching algorithms. Bolds values indicate higher accuracy achieved by a particular estimator for one specific CR.

CR No.	SPxy Index
	Area-Based Matching					Feature-Based Matching
	SC	NCC	MPC	OC	PC	BRISK	HARRIS	MEIGEN	FAST	BRISK_S	HARRIS_S	MEIGEN_S
53	55	70	55	100	30	19	51	29	-	77	51	29
54	135	175	65	55	95	122	42	52	382	102	42	52
56	90	90	85	77	90	71	101	81	61	11	101	81
51	50	-	40	55	32	135	44	44	-	265	44	44
55	75	70	55	20	104	160	90	90	200	160	90	90

show that the PC from the area-based and OC from feature-based categories provided better results than feature-based algorithms (see SP_xy indexes). HARRIS and MEIGEN detectors generally provided more accurate results than BRISK and FAST, whereas FAST had the worst performance among the all corner-based detectors. In cases of CR54, CR51 and CR55, the HARRIS and EIGEN results were identical when combined with the SURF descriptor. This means that in case of high pixel value changes, the detector and descriptor combination does not affect on the results.

To evaluate the performance of the feature-based matching algorithms, some evaluation metrics have been proposed. Ref. [69] defined the 1-accuracy and recall values of each image to assess the matching performance. The 1-accuracy and recall refer to the number of false matches relative to the total number of matches and the number of correctly matched regions with respect to the number of corresponding regions between two images of the same scene, respectively. According to [70], five different metrics are proposed to evaluate the detector and descriptor performance: putative match ratio, accuracy, matching score, recall and entropy. Since we used only one pair of the SAR images and the intended features on the images were only 16 CRs, we compared the achieved offsets with GPS measurements as Ground Control Point (GCP) to validate the performance of each algorithm. More information concerning a quantitative and qualitative comparison of the area and feature-based matching can be found in [71], while feature-based matching algorithms and performance comparison are described in [69,72,73]. A summary of the advantages and disadvantages of both area and feature-based matching are presented in

Table 11. Advantages and disadvantages of the area and feature-based matching techniques.

Matching Methods	Patch or Area-Based			Featured-Based
Image domain	spatial domain		frequency domain	frequency domain
Techniques	CC	NCC	PC	OC
Accuracy	Up to sub-pixel (by interpolation)	Up to sub-pixel (by interpolation)	Up to sub-pixel (by over sampling)	Up to sub-pixel
Function	Similarity	Similarity	Similarity—FFT	Orientation of intensity and FFT
Advantages	Simple and easy computation	- Invariant to linear brightness and contrast variations - Not too sensitive to translation and small rotation and scale changes	- Less sensitive to frequency dependent noise and varying illumination - Invariant to linear changes in brightness - Invariant to rotation	- Statistically robust - Illumination and scale invariant - Fast
Shortcoming	- Biased by changes in global brightness - Sensitive to intensity changes (varying Illumination)	- Sensitive to rotation, scale changes, different illumination, viewing angle and temporal changes - Flatness of peak	- Sensitive to spatial dependent noise and illumination - conditions	- More sensitive to local structural than intensity information

and

Table 12. Advantages and disadvantages of the feature-based matching algorithms regarding offset estimation.

Matching Method	Featured-Based
Feature style	Corner-based				Blob-based
Detector	BRISK	HARRIS	MEIGEN	FAST	SURF
Feature type	- Point tracking - Corners - multi-scale detection	- Point tracking - Corners - Single-scale detection	- Point tracking - Corners - Single-scale detection	- Point tracking - Corners - Single-scale detection	- Blob - Multiscale detection
Scale-Rotation	Invariant-Invariant	Variant-Invariant	Variant (scale)	Variant-Invariant	Invariant-Invariant
Descriptor	- Binary-based - Fast but Less accurate (localization)	-	-	-	- Distribution-based - Slower - More accurate (localization)

.

Finally, the velocity map of the CRs using integration of PSI, MAI, and offset tracking displacements (using the most accurate results derived by the related algorithms) is presented in Figure 14. The minimum 8.8 cm/year and maximum 31.6 m/year velocity rates were derived for CR6 and CR55, respectively, by the PSI and OC techniques. Based on the velocity map provided in Figure 14, three different geomorphological zones can be distinguished: (i) Accumulation zone including CRs4, 6, 8, 11; (ii) track zone including CRs13 and 53; and (iii) source zone including CRs23, 25, 28, 49, 57 and 58 [38].

6. Conclusions

Although the Corvara landslide has been the subject of the previous studies [36,39], they have faced with the intrinsic limitations of the techniques used. For example, PSI was not able to estimate the high velocity rate and non-LOS CRs and the differential DEM (UAV-based photogrammetry) derived from two subsequent acquisitions was only able to detect the vertical deformation limited only to the small part of the landslide (i.e., left-down side of CR58) due to the large extend of the landslide. In this research, these limitations have been overcome by using the integration of PSI, MAI, and offset tracking results, allowing the estimation of the displacements of the CRs over the whole part of the landslide.

The PSI results showed that the proper orientation and quality assessment parameters of CRs (i.e., PSLR; ISLR and IRF) have a key role in the noise error reduction. The provided sensitivity analysis model indicated that the uncertainty of the PSI measurements increases by deviating from the displacements azimuth with respect to the LOS azimuth. When displacement is aligned to the satellite azimuth, the displacement estimation is impossible (infinitive Std). Moreover, non-linearity behavior of the CRs motion in natural terrain could propagate some errors in the final extracted displacements when a pre-defined-based model of the PSI technique is used. In such case, non-predefined model methods should be considered.

The MAI result obtained for CR58 demonstrated that MAI provided the best-offset estimation among other offset-based estimators. This means that if displacement is aligned to N–S direction (nearly satellite path), MAI provides the highest accuracy up to 2.5% of the pixel size of CSK data (i.e., 2 m). This result could even be improved in case of having data with a higher coherence. Low coherence or a high coherent target surrounded by low coherent surface (in our case CR surrounded by vegetation) are the limiting factors to use higher multi-looking factors to increase MAI precision.

The accuracy of the amplitude offset tracking technique have been empirically estimated between about 1/10 to 1/30 of the pixel size for typical SAR systems. This accuracy corresponds to 20 cm and 6.6 cm of the pixel size of CSK data (i.e., 2 m) or 10% and 3.3% of the pixel size. The offset accuracy varied in xy directions, achieving from 0% of the pixel size (i.e., correct estimation) using a combination of the feature-based algorithms (e.g., MEIGEN_S for y offset of CR51) up to 1% of the pixel size using the phase correlation (e.g., PC for x offset of CR51). According to the results, not only the main objective of the paper was fulfilled (i.e., sub-pixel accuracy of offset estimation) but also a higher accuracy was obtained. The results were obtained when the random changes in pixel values occurred by CR tilting between two data acquisitions (i.e., at the worst-case scenario). Meanwhile, area and feature-based algorithms have been mainly developed to take into account the common geometric distortions (e.g., scale, rotation, and translation). Therefore, in normal conditions (with common distortions), the proposed approaches should provide more accurate and reliable results.

In general, the feature-based matching algorithms outperformed the area-based matching ones, which are usually used for offset estimation in the SAR data domain. The modularity of the feature-based algorithms allows us to combine each of corner and blob-based feature detection functions and descriptors. The combination of different algorithms leads to benefits from the capability of a given detector/descriptor (e.g., high localization accuracy of SURF descriptor) to compensate the weakness of other one (e.g., less localization accuracy of BRISK descriptor) or vice versa.

Upon inspecting the results, the provided survey on the offset tracking techniques shows that a single all-purpose algorithm to be able to extract offsets in all situations does not exist. Each of the different approaches has relative advantages and drawbacks, dependent on data properties, features and application.

In summary, although the InSAR-based techniques could provide more precise results, in cases of low coherence, high velocity rate and non-LOS movement, the area and feature-based matching techniques could be used as a robust alternative candidate for offset estimation.